Mattingly J.D., Heiser W.H., Pratt D.T. Aircraft Engine Design

Подождите немного. Документ загружается.

ENGINE SELECTION: PARAMETRIC CYCLE ANALYSIS 131

(l/h)

2.00

1.95

1.90

1.85

1.80

1.75

1.70

1.65

1.60

~=5

0.4

c¢=0

Target or Goal

25~m _m

95 100 105 110 115 120

F / rh 0 (lbfflbrrds)

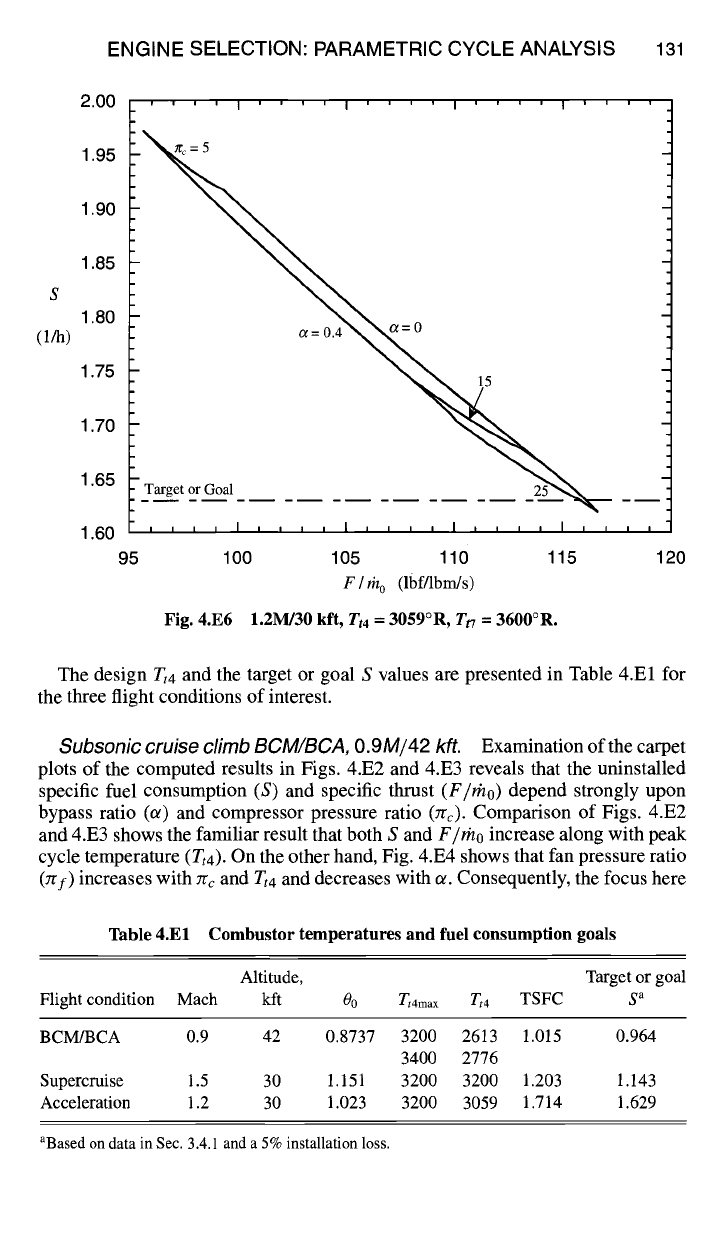
Fig. 4.E6 1.2M/30 kft, Tt4

3059°R, Tt7 = 3600°R.

The design Tt4 and the target or goal S values are presented in Table 4.El for

the three flight conditions of interest.

Subsonic cruise climb BCM/BCA,

0.9M/42 kft.

Examination of the carpet

plots of the computed results in Figs. 4.E2 and 4.E3 reveals that the uninstalled

specific fuel consumption (S) and specific thrust

(F/rho)

depend strongly upon

bypass ratio (or) and compressor pressure ratio (Trc). Comparison of Figs. 4.E2

and 4.E3 shows the familiar result that both S and

F/rho

increase along with peak

cycle temperature (Tt4). On the other hand, Fig. 4.E4 shows that fan pressure ratio

(:rf) increases with Jrc and

Tt4

and decreases with ~. Consequently, the focus here

Table 4.El Combustor temperatures and fuel consumption goals

Altitude, Target or goal

Flight condition Mach kft 0o

Tt4ma x Tt4

TSFC S a

BCM/BCA 0.9 42 0.8737 3200 2613 1.015 0.964

3400 2776

Supercruise 1.5 30 1.151 3200 3200 1.203 1.143

Acceleration 1.2 30 1.023 3200 3059 1.714 1.629

aBased on data in Sec. 3.4.1 and a 5% installation loss.

132 AIRCRAFT ENGINE DESIGN

will be upon the selection of useful ranges of t~ and Zrc, and consideration of

Tt'f

and Tt4 will be delayed pending later results.

Increasing ot alone causes both

F/rho

and S to decrease, in accordance with

normal expectations for subsonic turbofan engines, as the available exhaust kinetic

energy is spread over more incoming air. Because the slope of the line of constant

Zrc shows that

F/rho

is decreasing percentage-wise roughly twice as fast as S, it

does not seem advisable to choose an ot greater than 0.5. Conversely, because S

meets the target or goal for moderate to high pressure ratios, no a less than 0.3

should be considered. Thus, the best ~ for this flight condition is probably in the

range of 0.3-0.5.

Increasing Zrc alone produces a more complex behavior of

F/rho

and S because a

maximum of

F/rho

occurs while S continuously decreases. This behavior is typical

of turbine engines, as demonstrated in Refs. 1 and 2. The maximum value of

F/rho

is due to the simple fact that increasing values of Jrc (and thus

Tt3)

eventually limit

the amount of fuel than can be added before the allowable

Tt4

is reached. One should

logically select values of Zrc that are located below the knee of the curve, but not

so far below that

F/rho

is falling rapidly for slight reductions in S. Moreover, no

Zrc should be chosen that exceeds reasonable expectations, with that value today

being in the range of 35-40. Computations reveal, however, that Zrc cannot reach

that limit at high Mach flight conditions before

Tt3

exceed s current capabilities

(Zt3max >

1700°R). Taken together, these reasons indicate that Zrc should be held

in the range of 20-30 for this flight condition.

Supersonic penetration and escape dash,

1.5M/30 kft. Very similar re-

marks to those just stated, both qualitative and quantitative, can be made about the

influence of zrc, zrf, a, and

Tt4 on

S and

F/rho

at this flight condition. The main

differences, as illustrated by the carpet plot of Fig. 4.E5, are that

F/rho

decreases

more rapidly with zrc as well as less rapidly with a in the critical area below the

knee and that there is no sign of choking of the core flow at the highest allowable

values of zr¢. Taking these factors into account, including the special need for high

thrust at this flight condition, the useful ranges of parameters are 15 < Zrc < 25

and 0.3 < a < 0.4.

Supersonic acceleration,

1.2M/30 kft. The carpet plot of the computed

results in Fig. 4.E6 reveal that both S can be reduced and

F/mo

increased by

increasing 7r¢ and reducing ~. Again, changing either Tt4 or Tt7 would have the

usual effect of increasing both S and

F/rno.

By this time it has become clear that the desired fuel consumption goals can

be achieved at some flight conditions, but not all. Consequently, the focus of our

search must continue to be on reduced fuel consumption over the entire mission.

Otherwise, the takeoff weight

(WTo)

of the AAF will certainly grow beyond the

initial estimate of Chapter 3 and, because Eq. (3.49), which determines

Wro,

is extremely nonlinear,

Wro

could become unacceptably large. While it is still

possible that S will be reduced when the engine is throttled back to the required

thrust, or the installation penalties will be less than estimated, or the TSFC models

of Table 4.El are conservative, nothing may yet be taken for granted.

Consequently, the engine performance information generated at this flight condi-

tion shows that 20 < zr¢ < 30 and 0 < ~ < 0.4. The results obtained so far suggest

ENGINE SELECTION: PARAMETRIC CYCLE ANALYSIS 133

that Tt4 and

Tt7

must be limited in order to achieve acceptable fuel consumption,

even though increasing them will increase specific thrust and thereby reduce the

size of the required engine. Their limits will be arbitrarily selected

Zt4

~--

3200°R

and T,7 = 3600°R because even these values will push the material and cooling ca-

pabilities expected to be available for the AAF (see Table 4.4). These assumptions,

as well as any others, can be changed if later calculations indicate a positive benefit.

4.4.4 Integrated Results: Range of Design Choices

Before the final ranges of interest for key engine reference point parameters are

selected, two facts must be recognized. First, it makes sense to state them only in

conjunction with a specific flight condition (i.e., P0, To, and M0), preferably one

that will be near the final reference point. Because the AAF must operate well

over the 0.9 < M0 < 1.8/30-45 kft range, it is reasonable to conclude that the

reference point will be in the vicinity of 1.5M/35 kft. Second, any selection must

take into account the normal behavior of parameters when the engine is operating

off-design. A sensible goal is for the key engine parameters to be in their best

ranges at all critical operating points. Thus, the engine will appear to be properly

designed for each.

The three critical operating points were therefore added to scaled Figs. 4.6

and 4.8, which are representative of the type of engine emerging for the AAF

application, and the results reproduced here as Figs. 4.E7 and 4.E8.

0.0

I'''~1 'I'' I

I I , , I , J , ,

, , , ,

0.5 1.0 1.5 2.0 2.5

Alt (kft)

Fig. 4.E7 Compressor integrated results.

134 AIRCRAFT ENGINE DESIGN

0.6

0.5

0.4

0.3

I ' ' ' ' I ' ' ' ' I ' ' ' '

0.2 .... I .... I ,

~ , t , ~ , ~ I , ~ t

0.0 0.5 1.0 1.5 2.0 2.5

Alt (kft)

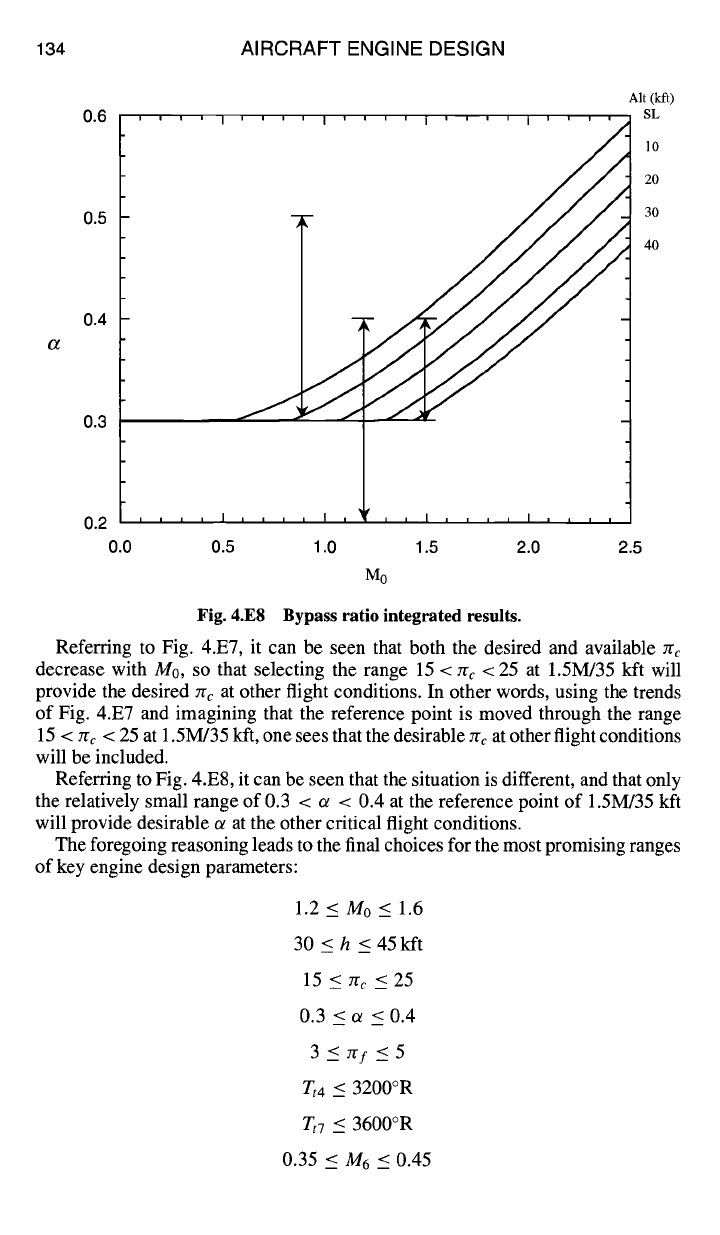
Fig. 4.E8 Bypass ratio integrated results.

Referring to Fig. 4.E7, it can be seen that both the desired and available 7rc

decrease with M0, so that selecting the range 15 < :re < 25 at 1.5M/35 kft will

provide the desired zrc at other flight conditions. In other words, using the trends

of Fig. 4.E7 and imagining that the reference point is moved through the range

15 < Zrc < 25 at 1.5M/35 lift, one sees that the desirable 7rc at other flight conditions

will be included.

Referring to Fig. 4.E8, it can be seen that the situation is different, and that only

the relatively small range of 0.3 < ot < 0.4 at the reference point of 1.5M/35 kft

will provide desirable ot at the other critical flight conditions.

The foregoing reasoning leads to the final choices for the most promising ranges

of key engine design parameters:

1.2_<Mo_< 1.6

30<h <45kft

15 < zr~ _< 25

0.3 <¢z <0.4

3_<7r/ ~5

Tt4 < 3200°R

Tt7 <

3600°R

0.35 < M6 < 0.45

ENGINE SELECTION: PARAMETRIC CYCLE ANALYSIS 135

A good first design should have both the compressor pressure ratio and the

combustor exit temperature at their maximum values at a theta break 00 equal to

the TR (see Appendix D). In this case the TR has initially been chosen to be 1.07,

which would correspond, for example, to 1.318 Mach at 30 kft or 1.454 Mach at

any altitude above the tropopause. Consequently, the selection of h depends on

the choice of M0 and vice versa.

4.4.5 Sensitivity Analysis

The power of the parametric engine cycle performance calculations can be

better understood and appreciated by means of this final investigation known as a

sensitivity analysis. This is a process in which the percentage change of all output

quantities with respect to the percentage change of each independent input quantity

is determined by varying the input parameters only slightly and one at a time. For

example, if one is interested in how sensitive the specific fuel consumption (S) is

to the cycle bypass ratio (~) alone, one would form the quantity

($2 - $1)/$1 ~S

(ot2 - o~1)/Oll got

from two successive reference point calculations that differ only in 6or << or. Such

ratios, in the limit, represent the mathematical slopes or derivatives that are gen-

erally too difficult to obtain in closed form for such a complex set of equations.

The qualitative meaning of these ratios is easy to grasp. When they are very small

compared to one, the input variable has little influence on the output variable. If the

entire array were very small compared to one, the design point would be located

on some type of a plateau, perhaps near to an optimum. Those ratios of the order

of one offer the opportunity for improvement and point out the desired direction

of change.

Consider the sensitivity of specific thrust and thrust specific fuel consumption to

changes in flight conditions and engine design choices for a mixed flow turbofan

engine having the component performance design values corresponding to those

of the printout reproduced in Sec. 4.2.7, which has the engine reference point

M0= 1.6 ~ = 0.4

Alt = 35k~

~4 =

3200 °R

~c = 16 ~7 = 3600 °R

~f = 3.8 Po/P9 = 1

Table 4.E2 presents the computed sensitivity of F/rho and S to changes in the

design choices at the engine reference point. These data were obtained from a

fractional change of +0.05 in each design choice given. Because S and F/rho are

at a minimum and maximum respectively for Po/P9 = 1.0, the sensitivities are

shown for a (+) and (-) variation in P0/P9. From the table, the sensitivity of thrust

specific fuel consumption to a change in bypass ratio, for example, is seen to be

- 0.0723 mil power

got

= +0.0341 max power

136

AIRCRAFT ENGINE DESIGN

Table 4.E2 Sensitivity analysis

Military power Maximum power

Fractional

Variation of/with F /rho S F /rho S

Tt 4

+1.0526 +0.5872 +0.2165 -0.0976

Tt7 +0.8437 +0.8411

rrc -0.0914 -0.1464 +0.0301 -0.0375

7/'f -0.0091 +0.0069 -0.0063 +0.0068

ot -0.2098 -0.0723 -0.0369 +0.0341

M6 -0.0026 +0.0034 -0.0022 +0.0023

Po/P9 -0.0039 +0.0034 -0.0033 +0.0034

+0.0042 -0.0052 +0.0035 -0.0045

Mo -0.5956 +0.0706 -0.1965 +0.0613

Alt +0.1900 -0.0362 +0.1109 -0.0715

neither of which shows a significant sensitivity of S to or. Fortunately, this insen-

sitivity is not typical of all of the results of the analysis.

Referring to Table 4.E2, and recalling that everything possible must be done to

reduce S, particularly at military power, there seem to be several useful indications,

namely:

1) An overall mission improvement in fuel consumption can be achieved by

reducing both

Tt4

and TtT, but only at the expense of a considerably larger reduction

in F/rho, and hence an increase in the size of the engine(s). The message here

confirms earlier conclusions regarding the necessity to put upper limits

Tt4

and

Tt7

in order to achieve fuel consumption goals. In that sense no real benefits result

from making the engine "hotter."

2) Relatively large changes of zr¢, zrf, and ot are required to measurably impact

F/rho and S, particularly in maximum power. The most promising possibility is

to increase Zrc, which improves both F/rho and S with and without afterburning.

Next in line for consideration is an increase of zrf, provided that the decrease of

military power F/rho is tolerable. Because changing ot has such conflicting effects,

no clear advice for its final selection is yet available.

3) Changing M6 has no performance consequences. Performance cannot be

improved by changing P9/Po and, as expected, it will suffer if P9 is taken far from

P0 and the exhaust nozzle is incorrectly expanded.

4) For completeness, the sensitivity of engine performance to reference point

Mach number and altitude has also been included. The large apparent benefits

of reducing Mach number and increasing altitude are illusory, because the flight

conditions are specified by the RFP and the gains would be lost when the engine

is returned to the present reference point (i.e., 1.5M/35 kft). Nevertheless, in order

to understand engine behavior more fully, recall that for any single exhaust stream

jet engine

F ~7ofh?R

mo aoMo

ENGINE SELECTION: PARAMETRIC CYCLE ANALYSIS 137

and

S- l'h f __

aoMo

F 7ohl, R

where 770 is the overall cycle energy conversion efficiency from fuel energy to thrust

work (see Appendix E). Because 7o varies relatively slowly with flight conditions,

the overwhelming effect of decreasing M0 or decreasing a0 (i.e., increasing alti-

tude) is to improve both F/mo and S. Thus, the ranges of M0 and h are retained

in the parameters only to allow the effects of different mission balance points to

be examined.

These sensitivity analysis results lead to the conclusions that 7gf and 7rc should

be selected from the high ends of their respective ranges, while

Tt4

and/or Tt7

should be allowed to drift down from their limiting values. Meanwhile, changes of

o~ and M16 will not have a significant impact on the leading propulsion performance

parameters.

References

IOates, G. C., The Aerothermodynamics of Gas Turbine and Rocket Propulsion, 3rd ed.,

AIAA Education Series, AIAA, Reston, VA, 1997.

2Mattingly, J. D., Elements of Gas Turbine Propulsion, McGraw-Hill, New York, 1996.

3"Gas Turbine Engine Performance Station Identification and Nomenclature." Society of

Automotive Engineers, Aerospace Recommended Practice (ARP) 755A, Warrendale, PA,

1974.

4Reynolds, W. C., and Perkins, H. C., Engineering thermodynamics, 2nd ed., McGraw-

Hill, New York, 1977.

5U.S. Dept. of Defense, "Model Specification for Engines, Aircraft, Turbojet," Military

Specification MIL-E-5008B, Washington, DC, Jan. 1959.

6Oates, G. C., "Performance Estimation for Turbofans with and Without Mixers," Journal

of Propulsion and Power, Vol. 1, No. 3, 1985, pp. 252-256.

7 Gordon, S., and McBride, B., "Computer Program for Calculation of Complex Chemical

Equilibrium Compositions," NASA SP-273, 1971.

Engine Selection: Performance Cycle Analysis

5.1 Concept

The parametric cycle analysis of Chapter 4 showed how reference point (design

point or on-design) engine performance was determined by design choices. This

made it possible to examine trends in engine specific performance (specific thrust

and thrust specific fuel consumption) with changes in design variables and to begin

to narrow the desirable range for each design parameter. Now that the first steps

have been taken toward finding an optimum engine for a particular application, it

is time to determine an engine's steady state operating performance.

The object of performance cycle analysis is to determine the engine's perfor-

mance over its operating envelope. The performance of several different engines

can then be compared to reveal trends in engine performance with design choices.

Thus, it is possible to focus in on the most promising designs and to ultimately

find the engine reference point that has the best balanced performance over the

whole mission spectrum. Once an engine cycle and its design choices are made,

the results of the performance cycle analysis are used to size the engine by the

methods presented in Chapter 6. The performance of a selected engine can also

serve to determine how well the thrust lapse model and the fuel consumption es-

timates, used in the constraint and mission analyses of Chapters 2 and 3, are met

by the engine.

Performance analysis differs significantly from parametric analysis. In paramet-

ric (reference or design point) cycle analysis all of the design choices (including the

flight conditions) are free to be selected by the designer, and the engine performance

characteristics per unit mass flow are determined for each selected set of choices.

In contrast, in performance cycle analysis the design choices have been made, and

the performance of this specific reference point engine is needed at all possible

operating conditions. The independent variables in performance analysis are flight

conditions, throttle settings, and nozzle settings. Once the engine is sized and the

mass flow rate specified, performance analysis is employed to determine how a

selected engine performs at all operating conditions within its flight envelope.

The mental image usually attached to this stage of development is that of an

engine of fixed configuration that we have manufactured for testing in a facility

that can simulate the desired flight conditions (see Appendix E). Although the

absolute size of the engine may be arbitrary during performance analysis, and we

may lack most of the details of the geometry of the individual components, it is

still best to think of it as a piece of hardware that we have built in order to explore

the behavior of this reference point engine.

For performance analysis, individual component performance can be modeled

as a function of operating conditions or actual component characteristics can

be obtained from component hardware performance data. These two approaches

139

140

AIRCRAFT ENGINE DESIGN

bleed air

Fig. 5.1a Reference stations---mixed stream turbofan engine.

correspond to varying degrees of accuracy. In the absence of actual component

hardware in a preliminary engine design, simple models of component perfor-

mance are used to give preliminary estimates of engine performance.

In the following section, relationships are developed for determining the engine

performance of the engine cycle whose parametric (reference point) performance

was covered in Chapter 4. The analysis is an extension of that presented in Refs. 1

and 2. The task now is to develop design tools in the form of equations and their

solution procedures that will permit determination of the component and hence

engine performance at any condition.

5.2 Design Tools

5.2.1

The Performance Problem

The performance of a selected design point mixed flow turbofan engine of the

type shown in Figs. 5.1a and 5.1b is desired at any flight conditions, throttle

settings, and nozzle settings. It is assumed that a parametric (design point) cycle

analysis has been performed for the reference point engine using the methods

of Chapter 4 to give so-called reference conditions (subscript R) for the engine

(SR, [F/FnO]R, etc.), for each engine component (TrfR, r/R, etc.), and for the flight

conditions (MoR, POR, and TOR).

To better understand the performance problem, it is instructive to review how the

parametric analysis proceeds. In the parametric cycle analysis, Eqs. (H. 1-H. 16) of

Appendix H constitute 16 independent equations for directly finding values of the

power extraction

PTOL PFOH

I~ bleed air

ire t

i corn

2.5

I cooling air #2 I~

cooling air #1

3.1 4 ~.L 4. l high-pre ..... turbine 4.4 J. 4.5 5

high-pressure spool I /

low-pressure spool

Fig. 5.1b Reference stations--bleed and turbine cooling air flows.

ENGINE SELECTION: PERFORMANCE CYCLE ANALYSIS

Table 5.1 Engine performance variables

141

Independent Constant Dependent

Component variable or known quantity variable

Engine M0, To, P0 /3 rn0,

Diffuser zra =

f(Mo)

Fan Of 2gf, "~f

Low-pressure compressor 0eL rrcL, r~c

High-pressure compressor

Ocn ZrcH, rc~

Burner T,4 ~rb f

Coolant mixer 1 e~

"Cm 1

High-pressure turbine 0tin M4 zr,H, rt~

Coolant mixer 2 e 2 rm2

Low-pressure turbine r/tL,

M4,5

rCtg, rtL

Mixer zrM

max,

A6,

JI'M, "gM, fit,

AI6,

A6A

m6, M16,

mra

Afterburner

T, 7 Yr aBdry, JT AB f AB

Exhaust nozzle

Po/ P9 re,, As a,y Ms, M9

Total number 6 24

16 dependent component performance variables in the order rf,

rcL, r.cH,

rml,

rtH, zrtH, rm2, rtC, ZrtL, Or', rM, MI~, M6A, zrM, and fAB

for given values of the inde-

pendent quantities consisting of flight conditions, aircraft system parameters, and

design choices. With values of these 16 component variables in hand, the engine

reference point performance in terms of

F/rho, S, tip,

and tire/is readily found.

Similarly, to find the engine performance, the operational performance values

of the 24 dependent variables listed in Table 5.1 must be determined and then, in

turn, related by 24 independent equations to obtain a solution for each component

performance variable. Because performance analysis is an indirect problem as

opposed to the direct problem of parametric analysis, the solution of the 24 perfor-

mance equations is not as straightforward as in the parametric case. Regardless of

the difficulty in solving the equations, once the values of the 24 dependent variables

in Table 5.1 are known, the engine performance in terms of

f, fAB, F/mo, S, tie,

and tirH follows immediately from Eqs. (4.18), (4.19), (4.14), (4.31), (4.32a), and

(4.32b), respectively.

Please notice in the "Constant or known variable" column of Table 5.1 that

Tgb, gAB,

and zr, are assumed to remain constant, that "Cd, 7rm2 , and rn are assumed

equal to one, and that 7gml is contained in rrtH. Also please be aware that, because

power extraction is considered in the analysis, a preliminary estimate of rn0 {Eq.

(4.33) and Table 4.1} is required to proceed with the performance analyses. The

correct value of rn0 is finally determined when the engine is sized (see Chapter 6).

5.2.2 Assumptions

The engine of interest is shown in Figs. 5.1a and 5.1b, where the notation

of Chapter 4 has been retained.

In addition to the assumptions summarized in

Sec. 4.2.6,

the following assumptions are employed in performance analysis: