Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.

t
2
¼ t
2
0
þ
x
2
V
2
where x is the offset between the source and the receiver, t
0
is the zero-offset,
two-way travel time, and V is the velocity of the layer. The increase in travel time
with distance, specifically the extra travel time relative to t
0
, is called normal
moveout (or NMO), and the velocity that determines the NMO, is called the
NMO velocity, V
NMO
. In the case of a homogeneous layer above a horizontal
reflector, V
NMO
¼ V.
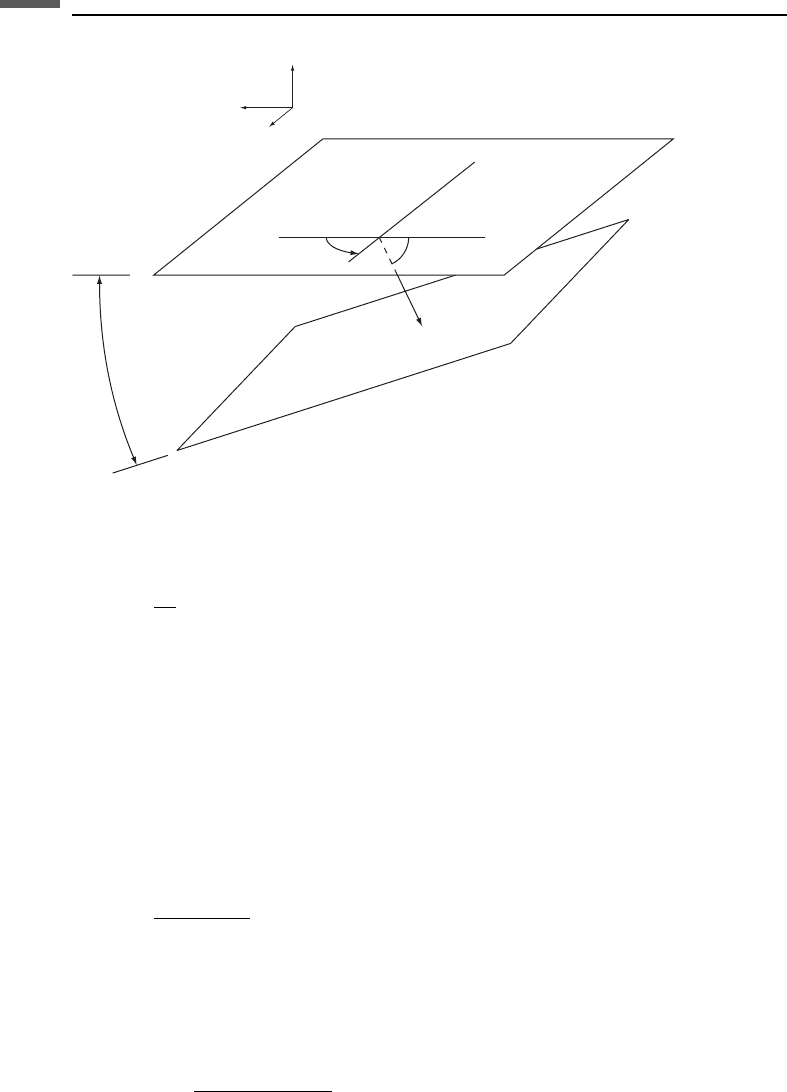
When the reflector is dipping with angle f from the horizontal (Figure 3.3.1), the
travel time equation in the vertical plane along dip becomes (Levin, 1971)
t
2
¼ t
2
0
þ
x
2
V= cos ðÞ
2
or V
NMO
ðÞ¼V= cos . Again, t
0
is the zero-offset, two-way travel time. More
generally, the azimuthally varying NMO velocity is (Levin, 1971)
V
2
NMO
; ðÞ¼
V
2
1 cos
2
sin
2
where f is the reflector dip and z is the azimuth relative to a horizontal axis in the dip
direction. Note that in the strike direction V
NMO
¼ V.
Surface
Reflector
Dip line
Strike line
Azimuth
Dip
f
θ
Zero-offset ray
x
1
x
2
x
3
Figure 3.3.1 Schematic showing the geometry for NMO with a dipping reflector.
87 3.3 NMO in isotropic and anisotropic media

When the Earth consists of horizontal, homogeneous, isotropic layers down to the
reflector, the two-way travel time equation is approximately hyperbolic, with the
approximation being best for small offsets:
t
2
t
2
0
þ
x
2
V
2
NMO
At zero dip, the NMO velocity is often approximated as the root mean squared
(RMS) velocity, V
NMO
V
RMS
, where
V
2
RMS
¼
X
N
i¼1
V
2
i
t
i
=
X
N
i¼1
t
i
where V
i
is the velocity of the ith layer and t
i
is the two-way, zero-offset travel time of
the ith layer. The summations are over all layers from the surface to the reflector. The
approximation V
NMO
V
RMS
is best at offsets that are small relative to the reflector
depth.
If the NMO velocity is estimated at two horizontal reflectors (e.g., V
NMO nðÞ
at the
base of layer n and V
NMO n1ðÞ
at the base of layer (n 1)), then the RMS equation
can be inverted to yield the Dix equation (Dix, 1955) for the interval velocity, V
n
,of
the nth layer:
V
2
n
1
t
n
V
2
NMO nðÞ
X
n
i¼1
t
i
V
2
NMO n1ðÞ
X
n1
i¼1
t
i
!
It is important to remember that this model assumes: (1) flat, homogeneous, isotropic
layers; (2) the offsets are small enough for the RMS velocity to be a reasonable
estimate of the moveout velocity; and (3) the estimated interval velocities are
themselves averages over velocities of thinner layers lying below the resolution of
the seismic data.
The equivalent of the Dix equation for anisotropic media is shown below.
NMO in an anisotropic Earth
For a heterogeneous elastic Earth with arbitrary anisotropy and arbitrary dip, the
NMO velocity of pure modes (at offsets generally less than the depth) can be written
as (Grechka and Tsvankin, 1998; Tsvankin, 2001)
1
V
2
NMO
ðÞ
¼ W
11
cos
2
þ 2W
12
sin cos þ W
22
sin
2
where z is the azimuth relative to the x
1
-axis. The components W
ij
are elements of a
symmetric matrix
~
W and are defined as W
ij
¼
0
@p
i
=@x
j
, where p
i
¼ @=@x
i
are
horizontal components of the slowness vector for rays between the zero-offset
reflection point and the surface location x
i
; x
j
, x
1
; x
2
ðÞis the one-way travel time
88 Seismic wave propagation

from the zero-offset reflection point, and t
0
is the one-way travel time to the CMP
(common midpoint) location x
1
¼ x
2
¼ 0. The derivatives are evaluated at the CMP
location. This result assumes a sufficiently smooth reflector and sufficiently smooth
lateral velocity heterogeneity, such that the travel time field exists (e.g., no shadow
zones) at the CMP point and the derivatives can be evaluated. This can be rewritten as
1
V
2
NMO
ðÞ
¼ l
1
cos
2
ðÞþl
2
sin
2
ðÞ
where l
1
and l
2
are the eigenvalues of
~
W, and is the rotation of the eigenvectors of
~
W relative to the coordinate system. l
1
and l
2
are typically positive, in which case
V
NMO
ðÞis an ellipse in the horizontal plane. The elliptical form allows the exact
expression for V
NMO
ðÞto be determined by only three parameters, the values of the
NMO velocity at the axes of the ellipse, and the orientation of the ellipse relative to
the coordinate axes. The elliptical form simplifies modeling of azimuthally varying
NMO for various geometries and anisotropies, since only V
NMO
ðÞalong the ellipse
axes needs to be derived. For example, we can write
1
V
2
NMO
ðÞ
¼
cos
2
V
2
NMO
¼ 0
ðÞ
þ
sin
2
V
2
NMO
¼ =2
ðÞ
where the axes of the ellipse are at ¼ 0 and ¼ =2.
A simple example of the elliptical form is the azimuthally varying moveout
velocity for a homogeneous, isotropic layer above a dipping reflector, given above,
which can be written as (Grechka and Tsvankin, 1998)
1
V
2
NMO
; ðÞ
¼
sin
2
V
2
þ
cos
2
V= cos ðÞ
2
where f is the dip and z is the azimuth relative to a horizontal axis in the dip
direction.
VTI symmetry with horizontal reflector
NMO velocities in a VTI medium (vertical symmetry axis) overlying a horizontal
reflector are given for P, SV, and SH modes (Tsvankin, 2001)by
V
NMO;P
0ðÞ¼V
P0
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
p
V
NMO;SV
0ðÞ¼V
S0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
p
; ¼
V
P0
V
S0
2
" ðÞ
V
NMO;SH
0ðÞ¼V
S0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
p
where V
P0
and V
S0
are the vertical P- and S-wave velocities, and e, d, and g are the
Thomsen parameters for VTI media. In this case, the NMO ellipse is a circle, giving
89 3.3 NMO in isotropic and anisotropic media

an azimuthally independent NMO velocity. These expressions for NMO velocity hold
for anisotropy of arbitrary strength (Tsvankin, 2001).
In the special case of elliptical anisotropy, with vertical symmetry axis, e ¼ d, the
expressions for NMO velocity become (Tsvankin, 2001):
V
NMO;P
0
ðÞ
¼ V
P0
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2"
p
V
NMO;SV
0ðÞ¼V
S0
V
NMO;SH
0ðÞ¼V
S0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
p
Vertical symmetry axis with dipping reflector
A dipping reflector creates an azimuthal dependence for the NMO velocity, even with
a VTI medium. For general VTI symmetry (vertical symmetry axis) and assuming
weak anisotropy, the NMO velocities overlying a dipping reflector are given for
P and SV modes by Tsvankin (2001). In the dip direction,
V
NMO;P
0;ðÞ¼
V
P0
1 þ ðÞ
cos
1 þ sin
2
þ 3 " ðÞsin
2
2 sin
2
V
NMO;SV
0;ðÞ¼
V
S0
1 þ ðÞ
cos
1 5 sin
2
þ 3 sin
4
; ¼
V
P0
V
S0
2
" ðÞ
where f is the dip, V
P0
and V
S0
are the vertical P- and S-wave velocities, and e, d, and
g are the Thomsen parameters for VTI media. In the strike direction with VTI
symmetry:
V
NMO;P
2
;
¼ V
P0
1 þ ðÞ1 þ " ðÞsin
2
2 sin
2
V
NMO;SV
2
;
¼ V
S0
1 þ ðÞ1 sin
2
2 sin
2
; ¼
V
P0
V
S0
2
" ðÞ
The complete azimuthal dependence can be easily written as an ellipse, where the
strike and dip NMO velocities are the semiaxes.
For the special case of elliptical symmetry (e ¼ d) of arbitrary strength anisotropy,
the dip-direction NMO velocities are (Tsvankin, 2001):
V
NMO;P
0;ðÞ¼
V
P0
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2"
p
cos
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2" sin
2
q
V
NMO;SV
0;ðÞ¼
V
S0
cos
V
NMO;SH
0;ðÞ¼
V
S0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
p
cos
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2 sin
2
q
90 Seismic wave propagation

where f is the layer dip angle. In the strike direction,
V
NMO;P
2
;
¼ V
P0
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2"
p
V
NMO;SV
2
;
¼ V
S0
V
NMO;SH
2
;
¼ V
S0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
p
Tilted TI symmetry with dipping reflector
For TI symmetry with symmetry axis tilting an angle n from the vertical and
assuming weak anisotropy, the NMO velocities are given by Tsvankin (2001). In
the dip direction
V
NMO;P
0;ðÞ¼
V
P0
cos
1 þ þ sin
2
nðÞþ3 " ðÞsin
2
nðÞ2 sin
2
nðÞ
þ
2 sin n sin nðÞ
cos
þ 2 " ðÞsin
2
nðÞ
V
NMO;SV
0;ðÞ¼
V
S0
cos
1 þ þ sin
2
nðÞ3 sin
2
nðÞ2 sin
2
nðÞ
þ 2
sin n sin nðÞcos 2 nðÞ
cos
where f is the reflector dip, V
P0
and V
S0
are the symmetry axis P- and S-wave
velocities, and e, d, and g are the Thomsen parameters for TI media. It is assumed that
the azimuth of the symmetry axis tilt is the same as the azimuth of the reflector dip. In
the strike direction, for weak tilted TI symmetry
V
NMO;P
2
;
¼ V
P0
1 þ ðÞ1 þ " ðÞsin
2
nðÞ2 sin
2
nðÞ
V
NMO;SV
2
;
¼ V
S0
1 þ ðÞ1 sin
2
nðÞ2 sin
2
nðÞ
¼
V
P0
V
S0
2
" ðÞ
In the special case of tilted elliptical symmetry with a tilted symmetry axis, the
NMO velocity in the dip direction is
V
NMO;P
0;ðÞ¼
V
P0
cos
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2 sin
2
nðÞ
q
1 2
sin n sin nðÞ
cos
1
V
NMO;SV
ðÞ¼
V
S0
cos
V
NMO;SH
0;ðÞ¼
V
S0
cos
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2 sin
2
nðÞ
q
1 2
sin n sin nðÞ
cos
1
91 3.3 NMO in isotropic and anisotropic media
In the strike direction for tilted elliptical symmetry
V
NMO;P
2
;
¼ V
P0
1 þ ðÞ
V
NMO;SV
2
;
¼ V
S0
Orthorhombic symmetry with horizontal reflector
We now consider an orthorhombic layer of arbitrary strength anisotropy over a
horizontal reflector. A symmetry plane of the orthorhombic medium is also horizontal.
The vertically propagating (along the x
3
-axis) P-wave velocity (V
P0
) and vertically
propagating S-wave velocities, polarized in the x
1
(V
S0
) and x
2
(V
S1
) directions are
V
P0
¼
ffiffiffiffiffiffiffiffiffiffiffi
c
33
=
p
; V
S0
¼
ffiffiffiffiffiffiffiffiffiffiffi
c
55
=
p
; V
S1
¼
ffiffiffiffiffiffiffiffiffiffiffi
c
44
=
p
where r is the density. Additional constants necessary for this discussion are
"
2ðÞ
¼
c
11
c
33
2c
33
2ðÞ
¼
c
13
þ c
55
ðÞ
2
c
33
c
55
ðÞ
2
2c
33
c
33
c
55
ðÞ
2ðÞ
¼
c
66
c
44
2c
44
ð2Þ
¼
V
P0
V
S0
2
"
2ðÞ
2ðÞ
hi
"
1ðÞ
¼
c
22
c
33
2c
33
1ðÞ
¼
c
23
þ c
44
ðÞ
2
c
33
c
44
ðÞ
2
2c
33
c
33
c
44
ðÞ
1ðÞ
¼
c
66
c
55
2c
55
ð1Þ
¼
V
P0
V
S1
2
"
1ðÞ
1ðÞ
hi
For a CMP line in the x
1
direction, the NMO velocities are
V
NMO;P
¼ 0;¼ 0
ðÞ
¼ V
P0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
2ðÞ
p
V
NMO;SV
¼ 0;¼ 0
ðÞ
¼ V
S0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
2ðÞ
p
V
NMO;SH
¼ 0;¼ 0ðÞ¼V
S1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
2ðÞ
q
where f is the dip and z is the azimuth measured from the x
1
-axis. For a line in the x
2
direction,
V
NMO;P
¼
2
;¼ 0
¼ V
P0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
1ðÞ
p
V
NMO;SV
¼
2
;¼ 0
¼ V
S1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
1ðÞ
p
V
NMO;SH
¼
2
;¼ 0
¼ V
S0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ 2
1ðÞ
q
92 Seismic wave propagation
NMO in a horizontally layered anisotropic Earth
The effective NMO for a stack of horizontal homogeneous layers above a dipping
reflector can be written as (Tsvankin, 2001)
V
2
NMO
¼
1
t
0
X
N
i¼1
V
iðÞ
NMO
p
ðÞ
hi
2
t
i
0
p
ðÞ
where t
i
0
pðÞis the interval travel time in layer i computed along the zero-offset ray,
t
0
¼
P
N
i¼1
t
i
0
is the total zero-offset time, and V
iðÞ
NMO
pðÞis the interval NMO velocity
for the ray parameter p of the zero-offset ray. The ray parameter for the zero-offset
ray is
p ¼
sin
V
N
ðÞ
where f is the reflector dip, and V
N
ðÞis the velocity at angle f from the vertical in
the Nth layer at the reflector.
Synopsis
The expressions for NMO in a layered and/or anisotropic elastic medium generally
work best for small offsets.
3.4 Impedance, reflectivity, and transmissivity
Synopsis
The impedance, I, of an elastic medium is the ratio of the stress to the particle velocity
(Aki and Richards, 1980) and is given by rV, where r is the density and V is the wave
propagation velocity. At a plane interface between two thick, homogeneous, iso-
tropic, elastic layers, the normal incidence reflectivity for waves traveling from
medium 1 to medium 2 is the ratio of the displacement amplitude, A
r
, of the reflected
wave to that of the incident wave, A
i
, and is given by
R
12
¼
A
r
A
i
¼
I
2
I
1
I
2
þ I
1
¼
2
V
2
1
V
1
2
V
2
þ
1
V
1
1
2
lnðI
2
=I
1
Þ
The logarithmic approximation is reasonable for |R| < 0.5 (Castagna, 1993).
A normally incident P-wave generates only reflected and transmitted P-waves.
A normally incident S-wave generates only reflected and transmitted S-waves. There
is no mode conversion.
93 3.4 Impedance, reflectivity, and transmissivity

The above expression for the reflection coefficient is obtained when the particle
displacements are measured with respect to the direction of the wave vector (equiva-
lent to the slowness vector or the direction of propagation). A displacement is taken to
be positive when its component along the interface has the same phase (or the same
direction) as the component of the wave vector along the interface. For P-waves, this
means that positive displacement is along the direction of propagation. Thus, a
positive reflection coefficient implies that a compression is reflected as a compres-
sion, whereas a negative reflection coefficient implies a phase inversion (Sheriff,
1991). When the displacements are measured with respect to a space-fixed coordin-
ate system, and not with respect to the wave vector, the reflection coefficient is
given by
R
12
¼
A
r
A
i
¼
I
1
I
2
I
2
þ I
1
¼
1
V
1
2
V
2
2
V
2
þ
1
V
1
The normal incidence transmissivity in both coordinate systems is
T
12
¼
A
t
A
i
¼
2I
1
I
2
þ I
1
¼
2
1
V
1
2
V
2
þ
1
V
1
where A
t
is the displacement amplitude of the transmitted wave. Continuity at the
interface requires
A
i
þ A
r
¼ A
t
1 þ R ¼ T
This choice of signs for A
i
and A
r
is for a space-fixed coordinate system. Note that
the transmission coefficient for wave amplitudes can be greater than 1. Sometimes the
reflection and transmission coefficients are defined in terms of scaled displacements
A
0
, which are proportional to the square root of energy flux (Aki and Richards, 1980;
Kennett, 1983). The scaled displacements are given by
A
0
¼ A
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
V cos
p
where y is the angle between the wave vector and the normal to the interface. The
normal incidence reflection and transmission coefficients in terms of these scaled
displacements are
R
0
12
¼
A
0
r
A
0
i
¼ R
12
T
0
12
¼
A
0
t
A
0
i
¼ T
12
ffiffiffiffiffiffiffiffiffiffi
2
V
2
p
ffiffiffiffiffiffiffiffiffiffi
1
V
1
p
¼
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
V
1
2
V
2
p
2
V
2
þ
1
V
1
Reflectivity and transmissivity for energy fluxes, R
e
and T
e
, respectively, are given
by the squares of the reflection and transmission coefficients for scaled displace-
ments. For normal incidence they are
94 Seismic wave propagation

R
e
12
¼
E
r
E
i
¼ R
0
12
2
¼
ð
1
V
1
2
V
2
Þ
2
ð
2
V
2
þ
1
V
1
Þ
2
T
e
12
¼
E
t
E
i
¼ T
0
12
2
¼
4
1
V
1
2
V
2
ð
2
V
2
þ
1
V
1
Þ
2
where E
i
, E
r
, and E
t
are the incident, reflected, and transmitted energy fluxes,
respectively. Energy reflection coefficients were first given by Knott (1899). Conser-
vation of energy at an interface where no trapping of energy occurs requires that
E
i
¼ E
r
þ E
t
1 ¼ R
e
þ T
e
The reflection and transmission coefficients for energy fluxes can never be greater
than 1.
Simple band-limited inverse of reflectivity time series
Consider a flat-layered Earth, with an impedance time series I
n
¼ nt
ðÞ
Vnt
ðÞ
,
where r is density, V is velocity (either P or S), and t ¼ nDt, where n ¼ 0,1,2, ...,N is
the normal incidence two-way travel time, equally sampled in intervals t. In these
expressions, nDt is the argument of r (·) and V(·), not a factor multiplying r and V.
The reflectivity time series can be approximated as
R
nþ1
¼
I
nþ1
I
n
I
nþ1
þ I
n
Solving for I
nþ1
yields a simple recursive algorithm
I
nþ1
¼ I
n
1 þ R
nþ1
ðÞ
1 R
nþ1
ðÞ
; n ¼ 0 : N 1
where I
0
, the impedance at time t ¼ 0, must be supplied. For small t and small R
n
,
this equation can be written as
I
n
I
0
exp
X
n
i¼1
2R
i
þ
2
3
R
3
i
þ
2
5
R
5
i
þ
"#
In contrast, a simple running summation of R
n
leads to
I
n
I
0
exp
X
n
i¼1
2R
i
ðÞ
"#
which is a low-order approximation of the first algorithm.
95 3.4 Impedance, reflectivity, and transmissivity

Rough surfaces
Random interface roughness at scales smaller than the wavelength causes incoherent
scattering and a decrease in amplitude of the coherent reflected and transmitted
waves. This could be one of the explanations for the observation that amplitudes of
multiples in synthetic seismograms are often larger than the amplitudes of corres-
ponding multiples in the data (Frazer, 1994). Kuperman (1975) gives results that
modify the reflectivity and transmissivity to include scattering losses at the interface.
With the mean-squared departure from planarity of the rough interface denoted by s
2
,
the modified coefficients are
~
R
12
¼ R
12
ð1 2k
2
1
2
Þ¼R
12
½1 8
2
ð=l
1
Þ
2
~
T
12
¼ T
12
1
1
2
ðk
1
k
2
Þ
2
2
¼ T
12
1 2
2
ðl
2
l
1
Þ
2
l
1
l
2
2
"#
where k
1
¼ o/V
1
, k
2
¼ o/V
2
are the wavenumbers, and l
1
and l
2
are the wavelengths
in media 1 and 2, respectively.
Uses
The equations presented in this section can be used for the following purposes:
to calculate amplitudes and energy fluxes of reflected and transmitted waves at
interfaces in elastic media;
to estimate the decrease in wave amplitude caused by scattering losses during
reflection and transmission at rough interfaces.
Assumptions and limitations
The equations presented in this section apply only under the following conditions:
normal incidence, plane-wave, time-harmonic propagation in isotropic, linear, elas-
tic media with a single interface, or multiple interfaces well separated by thick layers
with thickness much greater than the wavelength;
no energy losses or trapping at the interface; and
rough surface results are valid for small deviations from planarity (small s).
3.5 Reflectivity and amplitude variations with offset (AVO)
in isotropic media
Synopsis
The seismic impedance is the product of velocity and density (see Section 3.4), as
expressed by
96 Seismic wave propagation
