Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


Cubic: three independent constants
When each Cartesian coordinate plane is aligned with a symmetry plane of a material
with cubic symmetry, the Voigt elastic stiffness matrix has the following form:
c
11
c
12
c
12
000
c
12
c
11
c
12
000
c
12
c
12
c
11
000
000c
44
00
0000c
44
0
00000c
44
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
The corresponding nonzero cubic compliance tensor elements can be written in terms
of the stiffnesses:
s
11
¼
c
11
þ c
12
c
11
c
12
ðÞc
11
þ 2c
12
ðÞ
; s
12
¼
c
12
c
11
c
12
ðÞc
11
þ 2c
12
ðÞ
; s
44
¼
1
c
44
Energy considerations require that for a linear elastic material with cubic symmetry
the following conditions must hold:
c
44
0; c
11
> c
12
jj
; c
11
þ 2c
12
> 0
Hexagonal or transversely isotropic: five independent constants
When the axis of symmetry of a transversely isotropic material lies along the x
3
-axis,
the Voigt stiffness matrix has the form:
c
11
c
12
c
13
000
c
12
c
11
c
13
000
c
13
c
13
c
33
000
000c
44
00
0000c
44
0
00000c
66
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
; c
66
¼
1
2
ðc
11
c
12
Þ
The corresponding nonzero hexagonal compliance tensor elements can be written in
terms of the stiffnesses:
s
11
þ s
12
¼
c
33
c
33
c
11
þ c
12
ðÞ2c
2
13
; s
11
s
12
¼
1
c
11
c
12
s
13
¼
c
13
c
33
c
11
þ c
12
ðÞ2c
2
13
; s
33
¼
c
11
þ c
12
c
33
c
11
þ c
12
ðÞ2c
2
13
; s
44
¼
1
c
44
Energy considerations require that for a linear elastic material with transversely
isotropic symmetry the following conditions must hold:
c
44
0; c
11
> c
12
jj
; c
11
þ c
12
ðÞc
33
> 2c
2
13
27 2.2 Anisotropic form of Hooke’s law

Orthorhombic: nine independent constants
When each Cartesian coordinate plane is aligned with a symmetry plane of a material
with orthorhombic symmetry, the Voigt elastic stiffness matrix has the following
form:
c
11
c
12
c
13
000
c
12
c
22
c
23
000
c
13
c
23
c
33
000
000c
44
00
0000c
55
0
00000c
66
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
Monoclinic: 13 independent constants
When the symmetry plane of a monoclinic medium is orthogonal to the x
3
-axis, the
Voigt elastic stiffness matrix has the following form:
c
11
c
12
c
13
0 c
15
0
c
12
c
22
c
23
0 c
25
0
c
13
c
23
c
33
0 c
35
0
000c
44
0 c
46
c
15
c
25
c
35
0 c
55
0
000c
46
0 c
66
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
Phase velocities for several elastic symmetry classes
For isotropic symmetry, the phase velocity of wave propagation is given by
V
P
¼
ffiffiffiffiffiffi
c
11
r
V
S
¼
ffiffiffiffiffiffi
c
44
r
where r is the density.
In anisotropic media there are, in general, three modes of propagation (quasi-
longitudinal, quasi-shear, and pure shear) with mutually orthogonal polarizations.
For a medium with transversely isotropic (hexagonal) symmetry, the wave
slowness surface is always rotationally symmetric about the axis of symmetry.
The phase velocities of the three modes in any plane containing the symmetry axis
are given as
quasi-longitudinal mode (transversely isotropic):
V
P
¼ðc
11
sin
2
y þ c
33
cos
2
y þ c
44
þ
ffiffiffiffiffi
M
p
Þ
1=2
ð2Þ
1=2
quasi-shear mode (transversely isotropic):
V
SV
¼ðc
11
sin
2
y þ c
33
cos
2
y þ c
44
ffiffiffiffiffi
M
p
Þ
1=2
ð2Þ
1=2
28 Elasticity and Hooke’s law

pure shear mode (transversely isotropic):
V
SH
¼
c
66
sin
2
y þ c
44
cos
2
y
1=2
where
M ¼½ðc
11
c
44
Þsin
2
y ðc
33
c
44
Þcos
2
y
2
þðc
13
þ c
44
Þ
2
sin
2
2y
and y is the angle between the wave vector and the x
3
-axis of symmetry (y ¼0 for
propagation along the x
3
-axis). The five components of the stiffness tensor for a
transversely isotropic material are obtained from five velocity measurements: V
P
(0
),
V
P
(90
), V
P
(45
), V
SH
(90
), and V
SH
(0
) ¼ V
SV
(0
):
c
11
¼ V
2
P
ð90
Þ
c
12
¼ c
11
2V
2
SH
ð90
Þ
c
33
¼ V
2
P
ð0
Þ
c
44
¼ V
2
SH
ð0
Þ
and
c
13
¼c
44
þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4
2
V
4
Pð45
Þ
2V
2
Pð45
Þ
ðc
11
þ c
33
þ 2c
44
Þþðc
11
þ c
44
Þðc
33
þ c
44
Þ
q
For the more general orthorhombic symmetry, the phase velocities of the three
modes propagating in the three symmetry planes (XZ, YZ, and XY) are given as
follows:
quasi-longitudinal mode (orthorhombic, XZ plane):
V
P
¼ c
55
þ c
11
sin
2
y þ c
33
cos
2
y þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðc
55
þ c
11
sin
2
y þ c
33
cos
2
yÞ
2
4A
q
1=2
ð2Þ
1=2
quasi-shear mode (orthorhombic, XZ plane):
V
SV
¼ c
55
þ c
11
sin
2
y þ c
33
cos
2
y
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðc
55
þ c
11
sin
2
y þ c
33
cos
2
yÞ
2
4A
q
1=2
ð2Þ
1=2
pure shear mode (orthorhombic, XZ plane):
V
SH
¼
c
66
sin
2
y þ c
44
cos
2
y
1=2
where
A ¼ðc
11
sin
2
y þ c
55
cos
2
yÞðc
55
sin
2
y þ c
33
cos
2
yÞðc
13
þ c
55
Þ
2
sin
2
y cos
2
y
quasi-longitudinal mode (orthorhombic, YZ plane):
V
P
¼ c
44
þ c
22
sin
2
y þ c
33
cos
2
y þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðc
44
þ c
22
sin
2
y þ c
33
cos
2
yÞ
2
4B
q
1=2
ð2Þ
1=2
29 2.2 Anisotropic form of Hooke’s law

quasi-shear mode (orthorhombic, YZ plane):
V
SV
¼ c
44
þ c
22
sin
2
y þ c
33
cos
2
y
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðc
44
þ c
22
sin
2
y þ c
33
cos
2
yÞ
2
4B
q
1=2
ð2Þ
1=2
pure shear mode (orthorhombic, YZ plane):
V
SH
¼
c
66
sin
2
y þ c
55
cos
2
y
1=2
where
B ¼ðc
22
sin
2
y þ c
44
cos
2
yÞðc
44
sin
2
y þ c
33
cos
2
yÞðc
23
þ c
44
Þ
2
sin
2
y cos
2
y
quasi-longitudinal mode (orthorhombic, XY plane):
V
P
¼ c
66
þ c
22
sin
2
’ þ c
11
cos
2
’ þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðc
66
þ c
22
sin
2
’ þ c
11
cos
2
’Þ
2
4C
q
1=2
ð2Þ
1=2
quasi-shear mode (orthorhombic, XY plane):
V
SH
¼ c
66
þ c
22
sin
2
’ þ c
11
cos
2
’
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðc
66
þ c
22
sin
2
’ þ c
11
cos
2
’Þ
2
4C
q
1=2
ð2Þ
1=2
pure shear mode (orthorhombic, XY plane):
V
SV
¼
c
55
cos
2
’ þ c
44
sin
2
’
1=2
where
C ¼ðc
66
sin
2
’ þ c
11
cos
2
’Þðc
22
sin
2
’ þ c
66
cos
2
’Þðc
12
þ c
66
Þ
2
sin
2
’ cos
2
’
and y and ’ are the angles of the wave vector relative to the x
3
and x
1
axes,
respectively.
Kelvin notation
In spite of its almost exclusive use in the geophysical literature, the abbreviated Voigt
notation has several mathematical disadvantages. For example, certain norms of the
fourth-rank stiffness tensor are not equal to the corresponding norms of the Voigt
stiffness matrix (Thomson, 1878; Helbig, 1994; Dellinger et al., 1998), and the
eigenvalues of the Voigt stiffness matrix are not the eigenvalues of the stress tensor.
The lesser-known Kelvin notation is very similar to the Voigt notation, except that
each element of the 6 6 matrix is weighted according to how many elements of the
actual stiffness tensor it represents. Kelvin matrix elements having indices 1, 2, or 3
each map to only a single index pair in the fourth-rank notation, 11, 22, and 33,
30 Elasticity and Hooke’s law

respectively, so any matrix stiffness element with index 1, 2, or 3 is given a weight
of 1. Kelvin elements with indices 4, 5, or 6 each represent two index pairs (23, 32),
(13, 31), and (12, 21), respectively, so each element containing 4, 5, or 6 receives a
weight of
ffiffiffi
2
p
. The weighting must be applied for each Kelvin index. For example,
the Kelvin notation would map
^
c
11
¼ c
1111
,
^
c
14
¼
ffiffiffi
2
p
c
1123
,
^
c
66
¼ 2c
1212
. One way
to convert a Voigt stiffness matrix into a Kelvin stiffness matrix is to pre- and
post-multiply by the following weighting matrix (Dellinger et al., 1998):
100 0 0 0
010 0 0 0
001 0 0 0
000
ffiffiffi
2
p
00
000 0
ffiffiffi
2
p
0
000 0 0
ffiffiffi
2
p
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
yielding
^
c
11
^
c
12
^
c
13
^
c
14
^
c
15
^
c
16
^
c
12
^
c
22
^
c
23
^
c
24
^
c
25
^
c
26
^
c
13
^
c
23
^
c
33
^
c
34
^
c
35
^
c
36
^
c
14
^
c
24
^
c
34
^
c
44
^
c
45
^
c
46
^
c
15
^
c
25
^
c
35
^
c
45
^
c
55
^
c
56
^
c
16
^
c
26
^
c
36
^
c
46
^
c
56
^
c
66
0
B
B
B
B
B
B
B
B
@
1
C
C
C
C
C
C
C
C
A
¼
c
11
c
12
c
13
ffiffiffi
2
p
c
14
ffiffiffi
2
p
c
15
ffiffiffi
2
p
c
16
c
12
c
22
c
23
ffiffiffi
2
p
c
24
ffiffiffi
2
p
c
25
ffiffiffi
2
p
c
26
c
13
c
23
c
33
ffiffiffi
2
p
c
34
ffiffiffi
2
p
c
35
ffiffiffi
2
p
c
36
ffiffiffi
2
p
c
14
ffiffiffi
2
p
c
24
ffiffiffi
2
p
c
34
2c
44
2c
45
2c
46
ffiffiffi
2
p
c
15
ffiffiffi
2
p
c
25
ffiffiffi
2
p
c
35
2c
45
2c
55
2c
56
ffiffiffi
2
p
c
16
ffiffiffi
2
p
c
26
ffiffiffi
2
p
c
36
2c
46
2c
56
2c
66
0
B
B
B
B
B
B
B
B
@
1
C
C
C
C
C
C
C
C
A
where the
^
c
ij
are the Kelvin elastic elements and c
ij
are the Voigt elements.
Similarly, the stress and strain elements take on the following weights in the Kelvin
notation:
^
T ¼
^
1
¼
11
^
2
¼
22
^
3
¼
33
^
4
¼
ffiffiffi
2
p
23
^
5
¼
ffiffiffi
2
p
13
^
6
¼
ffiffiffi
2
p
12
2
6
6
6
6
6
6
6
6
4
3
7
7
7
7
7
7
7
7
5
;
^
E ¼
^
e
1
¼ e
11
^
e
2
¼ e
22
^
e
3
¼ e
33
^
e
4
¼
ffiffiffi
2
p
e
23
^
e
5
¼
ffiffiffi
2
p
e
13
^
e
6
¼
ffiffiffi
2
p
e
12
2
6
6
6
6
6
6
6
6
4
3
7
7
7
7
7
7
7
7
5
31 2.2 Anisotropic form of Hooke’s law

Hooke’s law again takes on the familiar form in the Kelvin notation:
^
1
^
2
^
3
^
4
^
5
^
6
0
B
B
B
B
B
B
@
1
C
C
C
C
C
C
A
¼
^
c
11
^
c
12
^
c
13
^
c
14
^
c
15
^
c
16
^
c
12
^
c
22
^
c
23
^
c
24
^
c
25
^
c
26
^
c
13
^
c
23
^
c
33
^
c
34
^
c
35
^
c
36
^
c
14
^
c
24
^
c
34
^
c
44
^
c
45
^
c
46
^
c
15
^
c
25
^
c
35
^
c
45
^
c
55
^
c
56
^
c
16
^
c
26
^
c
36
^
c
46
^
c
56
^
c
66
0
B
B
B
B
B
B
@
1
C
C
C
C
C
C
A
^
e
1
^
e
2
^
e
3
^
e
4
^
e
5
^
e
6
0
B
B
B
B
B
B
@
1
C
C
C
C
C
C
A
The Kelvin notation for the stiffness matrix has a number of advantages. The Kelvin
elastic matrix is a tensor. It preserves the norm of the 3 3 3 3 notation:
X
i;j¼1;...;6
^
c
2
ij
¼
X
i;j;k;l¼1;...;3
c
2
ijkl
The eigenvalues and eigenvectors (or eigentensors) of the Kelvin 6 6 C-matrix are
geometrically meaningful (Kelvin, 1856; Mehrabadi and Cowin, 1989; Dellinger
et al., 1998). Each Kelvin eigentensor corresponds to a state of the medium where
the stress and strain ellipsoids are aligned and have the same aspect ratios. Further-
more, a stiffness matrix is physically realizable if and only if all of the Kelvin
eigenvalues are non-negative, which is useful for inferring elastic constants from
laboratory data.
Elastic eigentensors and eigenvalues
The eigenvectors of the three-dimensional fourth-rank anisotropic elasticity tensor
are called eigentensors when projected into three-dimensional space. The maximum
number of eigentensors for any elastic symmetry is six (Kelvin, 1856; Mehrabadi and
Cowin, 1989). In the case of isotropic linear elasticity, there are two unique eigen-
tensors. The total stress tensor ~ and the total strain tensor
~
e for the isotropic case can
be decomposed in terms of the deviatoric second-rank tensors (~
dev
and
~
e
dev
) and
scaled unit tensors [
1
3
trð~Þ
~
I and
1
3
trð
~
eÞ
~
I]:
~ ¼ ~
dev
þ
1
3
trð~Þ
~
I
~
e ¼
~
e
dev
þ
1
3
trð
~
eÞ
~
I
For an isotropic material, Hooke’s law can be written as
~ ¼ l tr
~
eðÞ
~
I þ 2m
~
e
where l is Lame
´
’s constant and m is the shear modulus. However, if expressed in
terms of the stress and strain eigentensors, Hooke’s law becomes two uncoupled
equations:
tr ~ðÞ
~
I ¼ 3Ktr
~
eðÞ
~
I; ~
dev
¼ 2m
~
e
dev
32 Elasticity and Hooke’s law

where K is the bulk modulus. Similarly, the strain energy U for an isotropic material
can be written as
2U ¼ 2m tr
~
e
2
dev
þ Ktr
~
eðÞ½
2
where m and K scale two energy modes that do not interact.
Hence we can see that, although any two of the isotropic constants (l, m, K,
Young’s modulus, and Poisson’s ratio) can be derived in terms of the others, m and
K have a special significance as eigenelastic constants (Mehrabadi and Cowin, 1989)
or principal elasticities of the material (Kelvin, 1856). The stress and strain eigen-
tensors associated with m and K are orthogonal, as shown above. Such an orthogonal
significance does not hold for the pair l and m. Eigenelastic constants for a few other
symmetries are shown in Table 2.2.1, expressed in terms of the Voigt constants
(Mehrabadi and Cowin, 1989).
Poisson’s ratio defined for anisotropic elastic materials
Familiar isotropic definitions for elastic constants are sometimes extended to aniso-
tropic materials. For example, consider a transversely isotropic (TI) material with
uniaxial stress, applied along the symmetry (x
3
-) axis, such that
33
6¼ 0
11
¼
12
¼
13
¼
22
¼
23
¼ 0
One can define a transversely isotropic Young’s modulus associated with this
experiment as
E
33
¼
33
e
33
¼ c
33
2c
2
31
c
11
þ c
12
Table 2.2.1 Eigenelastic constants for several different symmetries.
Symmetry Eigenvalue
Multiplicity
of eigenvalue
Isotropic c
11
þ 2c
12
¼ 3K 1
2c
44
¼ 2m 5
Cubic c
11
þ 2c
12
1
c
11
c
12
2
2c
44
3
Transverse
Isotropy
c
33
þ
ffiffiffi
2
p
c
13
b þ
ffiffiffiffiffiffiffiffiffiffiffiffiffi
b
2
þ 1
p
; b ¼
ffiffi
2
p
4c
13
ðc
11
þ c
12
c
33
Þ 1
c
33
þ
ffiffiffi
2
p
c
13
b
ffiffiffiffiffiffiffiffiffiffiffiffiffi
b
2
þ 1
p
1
c
11
c
12
2
2c
44
2
33 2.2 Anisotropic form of Hooke’s law
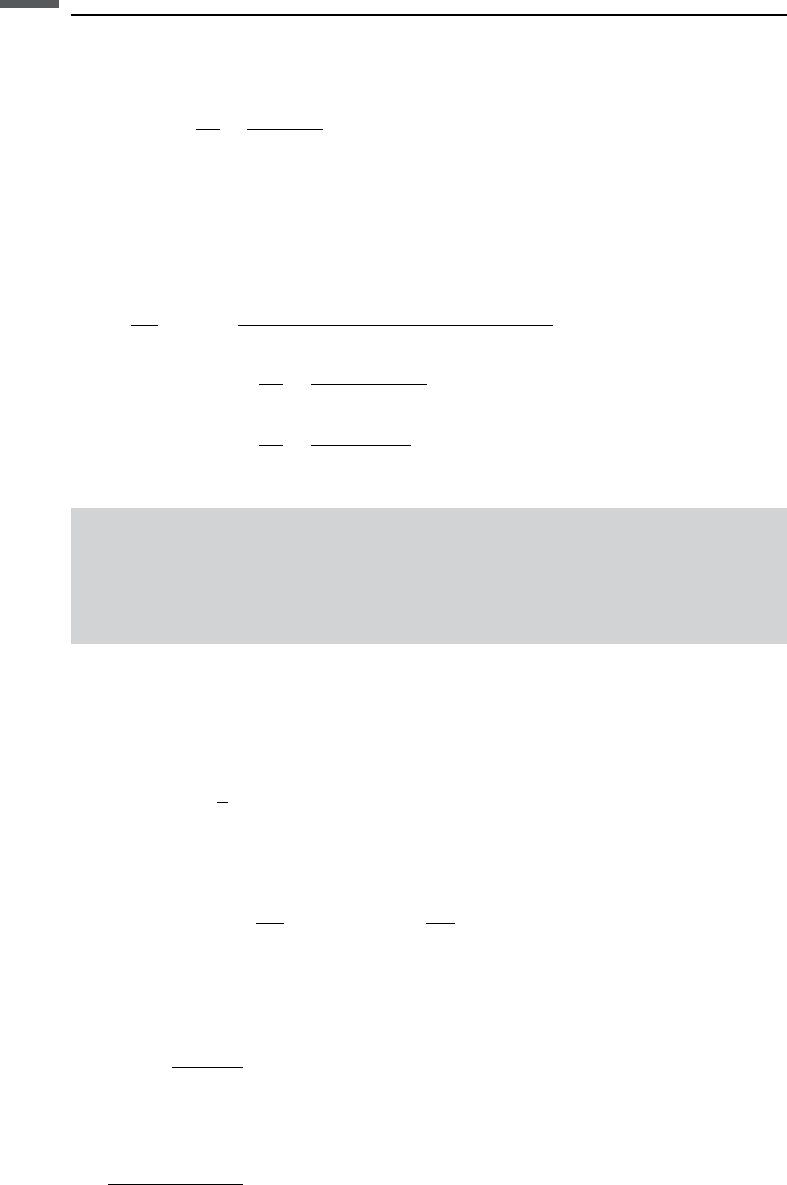
where the c
ij
are the elastic stiffnesses in Voigt notation. A pair of TI Poisson ratios
can similarly be defined in terms of the same experiment:
n
31
¼ n
32
¼
e
11
e
33
¼
c
31
c
11
þ c
12
If the uniaxial stress field is rotated normal to the symmetry axis, such that
11
6¼ 0
12
¼
13
¼
22
¼
23
¼
33
¼ 0
then one can define another TI Young’s modulus and pair of Poisson ratios as
E
11
¼
11
e
11
¼ c
11
þ
c
2
31
ðc
11
þ c
12
Þþc
12
ðc
33
c
12
þ c
2
31
Þ
c
33
c
11
c
2
31
n
13
¼ n
23
¼
e
33
e
11
¼
c
31
ðc
11
c
12
Þ
c
33
c
11
c
2
31
n
12
¼ n
21
¼
e
22
e
11
¼
c
33
c
12
c
2
31
c
33
c
11
c
2
31
Caution
Just as with the isotropic case, definitions of Young’s modulus and Poisson ratio
in terms of stresses and strains are only true for the uniaxial stress state. Definitions
in terms of elastic stiffnesses are independent of stress state.
In spite of their similarity to their isotropic analogs, these TI Poisson ratios have
several distinct differences. For example, the bounds on the isotropic Poisson ratio
require that
1 n
isotropic
1
2
In contrast, the bounds on the TI Poisson ratios defined here are (Christensen, 2005)
n
12
jj
1; n
31
jj
E
33
E
11
1=2
; n
13
jj
E
11
E
33
1=2
Another distinct difference is the relation of Poisson’s ratio to seismic velocities. In
an isotropic material, Poisson’s ratio is directly related to the V
P
/V
S
ratio as follows:
V
P
=V
S
ðÞ
2
¼
21 nðÞ
1 2nðÞ
or, equivalently,
n ¼
V
P
=V
S
ðÞ
2
2
2 V
P
=V
S
ðÞ
2
1
hi
34 Elasticity and Hooke’s law
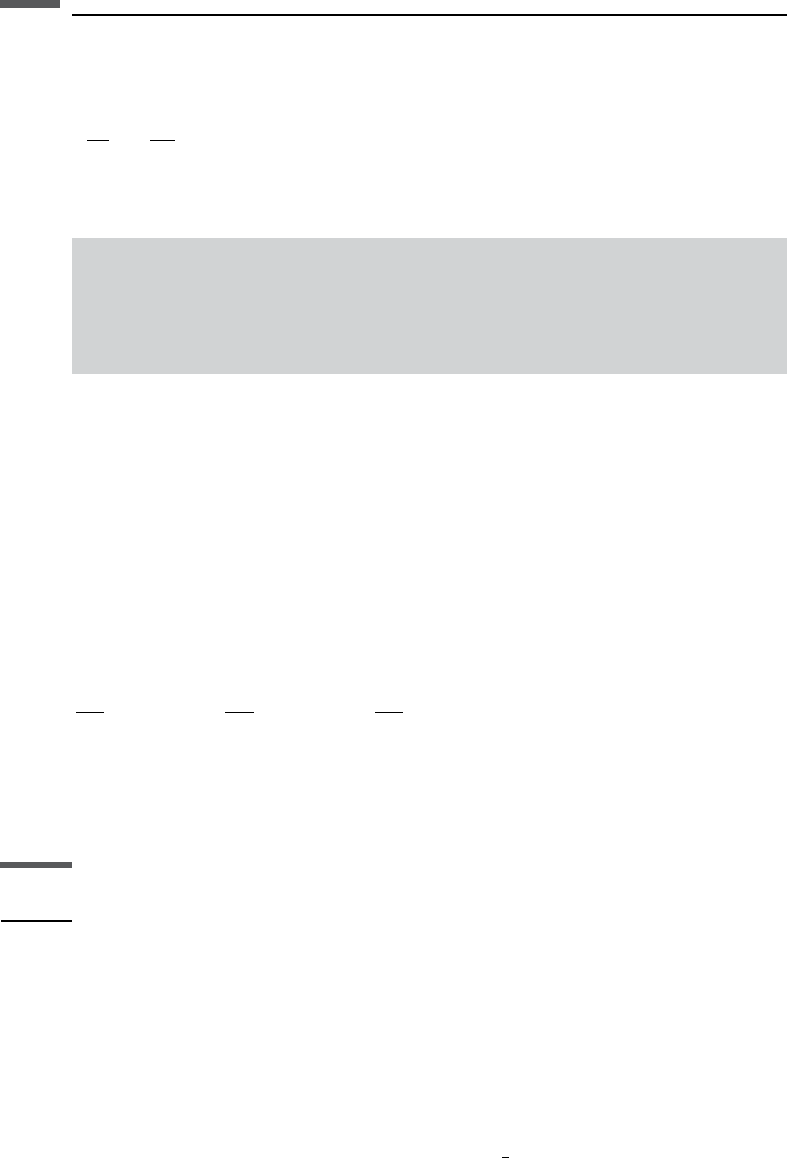
However, in the TI material, the ratio of velocities propagating along the symmetry
(x
3
-) axis is
V
P
V
S
2
¼
c
33
c
44
and is not simply related to the n
31
Poisson ratio.
Caution
The definition of Young’s modulus and Poisson’s ratio for anisotropic materials,
while possible, can be misinterpreted, especially when compared with isotropic
formulas.
For orthorhombic and higher symmetries, the “engineering” parameters – Poisson
ratios, n
ij
, shear moduli, G
ij
, and Young’s moduli, E
ij
– can be conveniently defined
in terms of elastic compliances (Jaeger et al., 2007):
E
11
¼ 1=s
11
n
21
¼s
12
E
22
G
12
¼ 1=s
66
E
22
¼ 1=s
22
n
31
¼s
13
E
33
G
13
¼ 1=s
55
E
33
¼ 1=s
33
n
32
¼s
23
E
33
G
23
¼ 1=s
44
Existence of a strain energy leads to the following constraints:
G
12
; G
13
; G
23
; E
11
; E
22
; E
33
> 0
E
11
E
22
ðn
21
Þ
2
< 1;
E
11
E
33
ðn
31
Þ
2
< 1;
E
22
E
33
ðn
32
Þ
2
< 1
Assumptions and limitations
The preceding equations assume anisotropic, linear elastic media.
2.3 Thomsen’s notation for weak elastic anisotropy
Synopsis
A transversely isotropic elastic material is completely specified by five independent
constants. In terms of the abreviated Voigt notation (see Section 2.2 on elastic
anisotropy) the elastic constants can be represented as
c
11
c
12
c
13
000
c
12
c
11
c
13
000
c
13
c
13
c
33
000
000c
44
00
0000c
44
0
00000c
66
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
; where c
66
¼
1
2
ðc
11
c
12
Þ
35 2.3 Thomsen’s notation for weak elastic anisotropy

and where the axis of symmetry lies along the x
3
-axis.
Thomsen (1986) suggested the following convenient notation for a TI material that
is only weakly anisotropic. His notation uses the P- and S-wave velocities (denoted
by a and b, respectively) propagating along the symmetry axis, plus three additional
constants:
a ¼
ffiffiffiffiffiffiffiffiffiffiffi
c
33
=
p
; b ¼
ffiffiffiffiffiffiffiffiffiffiffi
c
44
=
p
; e ¼
c
11
c
33
2c
33
g ¼
c
66
c
44
2c
44
; d ¼
ðc
13
þ c
44
Þ
2
ðc
33
c
44
Þ
2
2c
33
ðc
33
c
44
Þ
In terms of these constants, the three phase velocities can be approximated
conveniently as
V
P
ðyÞað1 þ d sin
2
y cos
2
y þ e sin
4
yÞ
V
SV
ðyÞb 1 þ
a
2
b
2
ðe dÞsin
2
y cos
2
y
V
SH
ðyÞbð1 þ g sin
2
yÞ
where y is the angle of the wave vector relative to the x
3
-axis; V
SH
is the wavefront
velocity of the pure shear wave, which has no component of polarization in the
symmetry axis direction; V
SV
is the pseudo-shear wave polarized normal to the pure
shear wave; and V
P
is the pseudo-longitudinal wave.
Berryman (2008) extends the validity of Thomsen’s expressions for P- and quasi-
SV-wave velocities to wider ranges of angles and stronger anisotropy with the
following expressions:
V
P
ðyÞa 1 þ e sin
2
y ðe dÞ
2 sin
2
y
m
sin
2
y cos
2
y
1 cos 2y
m
cos 2y
V
SV
ðyÞb 1 þ
a
2
b
2
ðe dÞ
2 sin
2
y
m
sin
2
y cos
2
y
1 cos 2y
m
cos 2y
where
tan
2
y
m
¼
c
33
c
44
c
11
c
44
Berryman’s formulas give more accurate velocities at larger angles. They are
designed to give the angular location of the peak (or trough) of the quasi-SV-velocity
closer to the correct location; hence, the quasi-SV-velocities are more accurate than
those from Thomsen’s equations. Thomsen’s P-wave velocities will sometimes be
more accurate than Berryman’s at small y and sometimes worse.
For weak anisotropy, the constant e can be seen to describe the fractional difference
between the P-wave velocities parallel and orthogonal to the symmetry axis (in the
weak anisotropy approximation):
36 Elasticity and Hooke’s law
