McMahon D. String Theory Demystified
Подождите немного. Документ загружается.


26
String Theory Demystifi ed
This allows us to write the action in the form
Smd XX=− −
∫
τη
µν
µν
(2.9)
This action is a nice compact form that allows us to derive the equations of motion.
As you recall from your studies of classical mechanics or quantum fi eld theory, the
quantity in the integrand is called the lagrangian:
Lm XX mX=− − =− −
η
µν
µν
2
There are two problems with the action so far developed in Eq. (2.9). First, think
about what happens in the case of a massless particle. Setting
m = 0
leaves us with
S → 0
and so there is nothing to vary to obtain the equations of motion. So this
action isn’t very helpful in the case of a massless particle. Also, it turns out that
quantization is not easy when we have a square root in the action. For these reasons,
we introduce an auxiliary fi eld that we will denote
a()
τ
and consider the
lagrangian
L
a
X
m
a=−
1
22
2
2
We can use this to defi ne an alternative expression for the action
′
=−
⎛
⎝
⎜
⎞
⎠
⎟
∫
Sd
a
Xma
1
2
1
22
τ
(2.10)
We can vary this action to fi nd an equation of motion for the auxiliary fi eld
a(
)
τ
. We
fi nd
δδτ
τδ
′
=−
⎛
⎝
⎜
⎞
⎠
⎟
=
⎛
⎝
⎜
⎞
⎠
⎟
∫
∫
Sd
a
Xma
d
a
X
1
2
1
1
2
1
22
2
−−
⎛
⎝
⎜
⎞
⎠
⎟
=−−
⎛
⎝
⎜
⎞
⎠
⎟
∫
δ
τ
()ma
d
a
Xm
2
2
22
1
2
1

CHAPTER 2 Equations of Motion
27
Now we set
δ
′
=S
0
. Since this means that the integrand must be 0, we obtain the
equation
−−=
⇒+ =
1
0
0
2
22
222
a
Xm
Xma
This is the equation of motion for the auxiliary fi eld. From this we fi nd an expression
for the auxiliary fi eld given by
a
X
m
=−
2
2
(2.11)
Using Eq. (2.11), we can show that the action in Eq. (2.10) is equivalent to Eq. (2.8),
which we do in the next example.
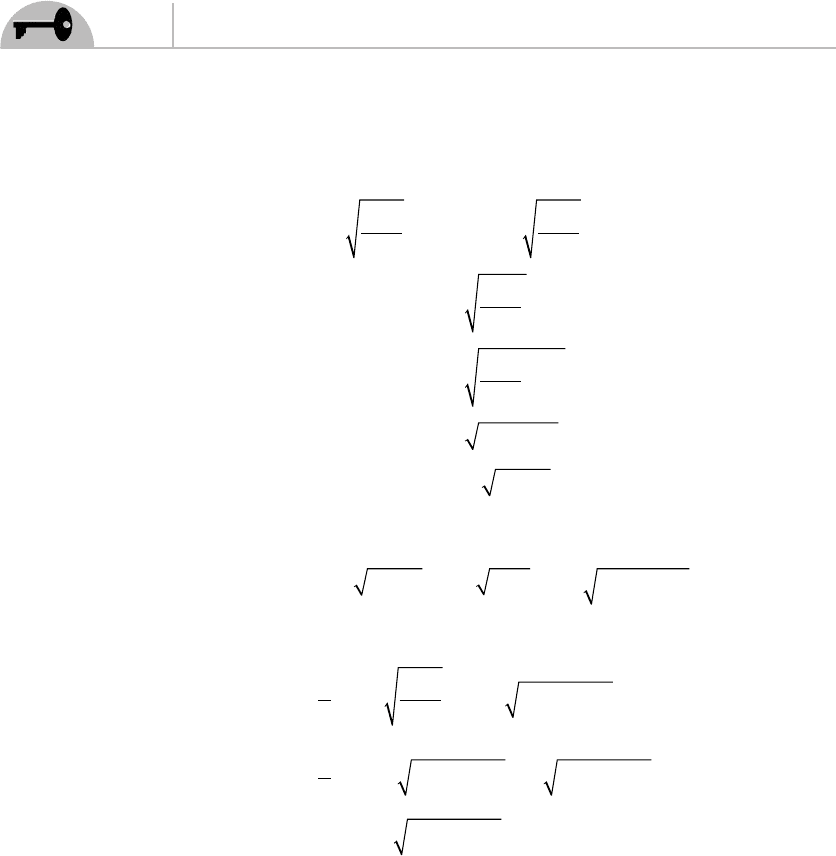
EXAMPLE 2.2
Show that if
aXm=−(/)
/
2212
, the action
′
=−
∫
SdaXma12 1
22
/[(/) ]
τ
can be recast
in the form
S m dX dX=− −
∫
η
µν
µν
.
SOLUTION
Let’s start by recalling that
XXX
2
=
η
µν
µν
. So we can rewrite the action
′
S
in the
following way:
′
=−
⎛
⎝
⎜
⎞
⎠
⎟
=
−
−−
∫
∫
Sd
a
Xma
d
m
X
Xm
1
2
1
1
2
22
2
2
22
τ
τ
XX
m
d
m
X
XmX
d
2
2
2
2
22
1
2
1
2
⎛
⎝
⎜
⎞
⎠
⎟
=
−
−−
⎛
⎝
⎜
⎞
⎠
⎟
=
∫
τ
τ
∫∫
−
−−
⎛
⎝
⎜
⎞
⎠
⎟
m
X
Xm XX
2
2
2
η
µν
µν
28
String Theory Demystifi ed
Now, let’s use a simple algebraic trick to rewrite the fi rst term. Remember from
complex variables that
i
2
1=−
. This means that
−
=− −
−
=−
−
=−
−
m
X
X
m
X
X
m
X
iX
2
2
2
2
2
2
2
2
22
11
()()
mm
X
iX
miX
miX
2
2
44
24 2
42
=− −
=− −
But
i
4
1=+
, and so
−− =−−=−−miXmXm XX
42 2
η
µν
µν
. Therefore the
action is
′
=
−
−−
⎛
⎝
⎜
⎞
⎠
⎟
=−
∫
∫
Sd
m
X
Xm XX
dm
1
2
1
2
2
2
2
τη
τ
µν
µν
ηηη
τη
µν
µν
µν
µν
µν
µν
XX m XX
md XX
−−
()
=− −
()
=
∫
SS
This demonstrates that the two actions are equivalent.
Strings in Space-Time
At this point we have reviewed some basic techniques that help us calculate the
equations of motion for a free relativistic point particle. We are going to extend this
work to the case of a string moving in space-time. A point particle has no extent
whatsoever, so can be described as a zero-dimensional object. We have seen that its

CHAPTER 2 Equations of Motion
29
motion can be described by saying that a point particle (zero-dimensional) sweeps
out a path or line in space-time (one dimension) that we call the world-line. A
string, unlike a point particle, has some extension in one dimension, so it’s a one-
dimensional object. As it moves, the string (one-dimensional) sweeps out a two-
dimensional surface in space-time that scientists call a worldsheet. For example,
imagine a closed loop of string moving through space-time. The worldsheet in this
case will be a tube, as shown in Fig. 2.1.
We can summarize this in the following way:
• The path of a point particle is a line in space-time. A line can be
parameterized by a single parameter, which is the proper time.
• As a string moves through space-time it sweeps out a two-dimensional
surface called a worldsheet. Since the worldsheet is two-dimensional, we
need two parameters, which we can generally denote by
ξξ
12
and
.
Locally the coordinates
ξξ
12
and
can be thought of as coordinates on the worldsheet.
Or, another way to look at this is to parameterize the worldsheet, we need to
account for proper time and the spatial extension of the string. So, the fi rst parameter
ct
Figure 2.1 The world-sheet of a closed string is a tube in space-time.

30
String Theory Demystifi ed
is once again the proper time
τ
,
and the second parameter, which is related to the
length along the string, is denoted by
σ
:
ξτ ξσ
12
==
Coordinates on the worldsheet
(, )
τσ
are mapped onto space-time by the functions
(called the string coordinates)
X
µ
τσ
(, )
(2.12)
So time and spatial position on the string are mapped onto the spatial coordinates in
(d + 1) dimensional space-time as
{ (,), (,), , (,)}XX X
d01
τσ τσ τσ
…
Now, we need to write down the action for the string which will generalize
Eq. (2.8) to our new higher-dimensional world, that is, to the case of the worldsheet.
This is done in the following way. Recall that the action of a point particle is
proportional to the length of its world-line [Eq. (2.5)]. We just noted that a string
sweeps out a two-dimensional worldsheet in space-time. This tells us that if we are
going to generalize the notion of the action of a point particle, we might expect that
the action of a string is proportional to the surface area of the worldsheet. This is in
fact the case. Anticipating that the constant of proportionality will turn out to be the
string tension, we can write this action as
STdA=−
∫
(2.13)
where dA is a differential element of area on the worldsheet. To fi nd the form of
dA
, we start by considering a differential line element
ds
2
and introduce coordinates
on the worldsheet as
ξτ ξσ
12
==and
. Doing a little algebra we have
ds dX dX
XX
dd
2
=−
=−
∂
∂
∂
∂
η
η
ξξ
ξξ
µν
µν
µν
µ
α
ν
β
αβ
This allows us to defi ne an induced metric on the worldsheet. This is given by
γη
ξξ
αβ µν
µ
α
ν
β
=
∂
∂
∂
∂
XX
(2.14)

CHAPTER 2 Equations of Motion
31
This metric determines distances on the worldsheet. We say that this metric is
induced because it includes the metric of the background space-time in its defi nition
(we are taking space-time to be fl at, so are using
η
µν
). That is to say, on the surface
of the worldsheet, there is a new measure of distance, but that measure of distance
is determined by the background space-time through its metric (which in general,
is not
η
µν
). Proceeding, we now have
ds d d
2
=
γξξ
αβ
αβ
Using the notations
X
X
X
X
µ
µ
µ
µ
τσ
=
∂
∂
′
=
∂
∂
We can write the components of the induced metric (for the case of fl at space-
time) as
γη
ττ
γη
στ
ττ µν
µν
στ µν
µν
=
∂
∂
∂
∂
=
=
∂
∂
∂
∂
=⋅
′
XX
X
XX
X
2
XX
XX
XX
X
==
∂
∂
∂
∂
=
∂
∂
∂
∂
=
′
γη
τσ
γη
σσ
τσ µν
µν
σσ µν
µν
2
(2.15)
Using Eq. (2.15), we can write the induced metric as a matrix in
(,
)
τσ
space
γ
αβ
=
⋅
′
⋅
′′
⎛
⎝
⎜
⎞
⎠
⎟
XXX
XX X
2
2
(2.16)
Notice that the determinant of this matrix is given by
γγ
α
β
==
′
−⋅
′
det ( )
XX X X
22 2
(2.17)
Let’s go back to where we started, seeking an expression for the action
STdA=−
∫

32
String Theory Demystifi ed
From elementary calculus, we know that in a given space described by a metric
G
α
β
,
an element of surface area is written as
dA G d=−det
αβ
ξ
2
In our case, the metric we need is the induced metric [Eq. (2.15)]. So we take
dA d d=−
γτσ
. If we integrate from some initial proper time
τ
i
to some fi nal
proper time
τ
f
and over the length of the string (which we’ll denote as
C
) then the
action can be written as
STdd
i
f
=− −
∫∫
τσγ
τ
τ
0
C
(2.18)
Or explicitly, using Eq. (2.17)
STddXX XX
i
f
=−
′
−⋅
′
∫∫
τσ
τ
τ
0
22 2
C
()
(2.19)
The actions in Eqs. (2.18) and (2.19) are called the Nambu-Goto action, which
describes the dynamics of a (classical) relativistic string. As the motion of a point
particle in space-time serves to minimize the length of the world-line, the motion of a
classical string in space-time acts to minimize the surface area of the worldsheet
.
Before moving ahead to a quantum theory of strings, we need to fi nd the equations
of motion for the string which we can then later quantize.
Equations of Motion for the String
Now that we have the action in place (and hence the lagrangian) we can obtain the
equations of motion for the string. We do this using the action principle, which tells
us to vary the action and set the result to 0
δ
S = 0
When computing the variation of the action, we will derive the equations of motion that
will be a partial differential equations—meaning that we will need to specify boundary
conditions in order to solve them. There are two different types of strings we need to
consider when looking at boundary conditions: open strings and closed strings.
If a string is open, this means exactly what it says, that the string is a free piece
of string with loose ends moving through space-time. The worldsheet in this case

CHAPTER 2 Equations of Motion
33
is a strip, and by convention we write the endpoint as
σπ
= .
There are two types
of boundary conditions that are possible for open strings. The fi rst is called Neumann
or free endpoint boundary conditions. We can write this boundary condition in
terms of the lagrangian or the conjugate momentum:
δ
δ
µ
σπ
µ
σ
σπ
L
X
P
′
==
=
=
0
0
00
,
,
or (Neumann)
(2.20)
Another way to write Neumann boundary conditions for the open string is
∂
∂
==
X
µ
σ
σπ
00when ,
(2.21)
In this case, no momentum can fl ow off the ends of the string. This indicates that
the ends of the string are free to move about space-time. On the other hand, suppose
that the ends of the string are fi xed instead. In that case we have Dirichlet or fi xed
point boundary conditions. These are given by
δ
δ
τ
µ
σπ
µ
σπ
L
X
X
=
=
=
∂
∂
=
0
0
00
,
,
or (Dirichlet)
(2.22)
A closed string is a little loop moving through space-time. In this case, the worldsheet
is a cylinder or a tube. The boundary conditions are periodic, described by
XX
µµ
τσ τσ π
(, ) (, )=+
(2.23)
Now let’s write down the conjugate momenta for the string. First recall the
lagrangian
LTXX XX=− ⋅
′
−
′
()()()
222
The conjugate momentum corresponding to the coordinate s is
P
L
XX
TXX XX
T
µ
σ
µµ
=
∂
∂
′
=
∂
∂
′
−⋅
′
−
′
()
=−
()()()
222
2
(()()() ()
/
XX X X XX X X⋅
′
−
′
⎡
⎣
⎤
⎦
⋅
′
−
−
222
12
22
µ
22
2
22
′
⎡
⎣
⎤
⎦
=−
⋅
′
−
′
⋅
′
−
X
T
XX X XX
XX X
µ
µµ
()
()()
(()
′
X
2
(2.24)

34
String Theory Demystifi ed
and we also have a conjugate momentum corresponding to the coordinate
τ
:
P
L
XX
TXX XX
T
µ
τ
µµ
=
∂
∂
=
∂
∂
−⋅
′
−
′
()
=−
()()()
222
2
(()()() ()
/
XX X X XX X X⋅
′
−
′
⎡
⎣
⎤
⎦
⋅
′′
−
′
−
222
12
22
µ
22
2
22
X
T
XX X X X
XX X
µ
µµ
⎡
⎣
⎤
⎦
=−
⋅
′′
−
′
⋅
′
−
()
()()
(()
′
X
2
(2.25)
Now, let’s vary the action to obtain the equations of motion for the string. First, if
it’s been awhile since you’ve had fi eld theory, convince yourself that
δδ
ττ
δ
δδ
σ
µ
µ
µ
µ
µ
X
X
X
X
X
=
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
=
∂
∂
′
=
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
()
==
∂
∂
σ
δ
µ
()X
Then, we can vary the action, and using the conjugate momenta we get
δτσ
τ
δ
σ
δ
τ
τ
µ
µ
µ
STdd
L
X
X
L
X
X
i
f
=−
∂
∂
∂
∂
+
∂
∂
′
∂
∂
∫∫
0
() (
µµ
τ
τ
µ
τµ
µ
σ
τσ
τ
δ
σ
δ
)
() (
⎡
⎣
⎢
⎤
⎦
⎥
=−
∂
∂
+
∂
∂
∫∫
Td d X
i
f
0
ΠΠ
XX
µ
)
⎡
⎣
⎢
⎤
⎦
⎥
We can rewrite this expression so that we can get terms multiplied by
δ
µ
X
by using
the product rule from calculus. For example,
∂
∂
(
)
=
∂
∂
+
∂
∂
⇒
∂
∂
=
∂
τ
δ
τ
δδ
τ
τ
δ
µ
τµ
µ
τµµ
µ
τ
µ
τµ
PX P X X
P
PX
∂∂
(
)
−
∂
∂
τ
δδ
τ
µ
τµ µ
µ
τ
PX X
P
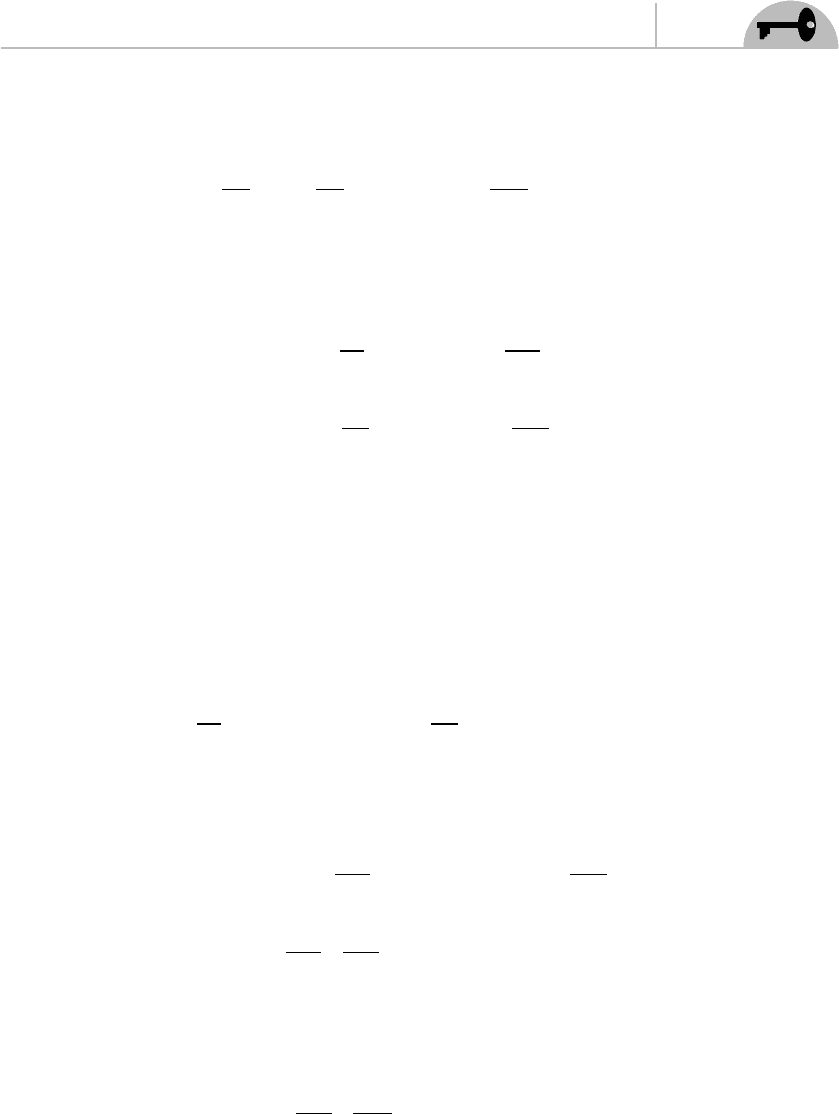
CHAPTER 2 Equations of Motion
35
Similarly,
PX PXX
P
µ
σµ
µ
σµ µ
µ
σ
σ
δ
σ
δδ
σ
∂
∂
=
∂
∂
()
−
∂
∂
This means that the variation of the action can be written as
δτσ
τ
δδ
τ
τ
τ
µ
τµ µ
µ
τ
STdd PX X
P
i
f
=−
∂
∂
()
−
∂
∂
⎡
⎣
⎢
⎢
⎤
∫∫
0
C
⎦⎦
⎥
⎥
−
∂
∂
()
−
∂
∂
⎡
⎣
⎢
⎢
∫∫
Tdd PX X
P
i
f
τσ
σ
δδ
σ
τ
τ
µ
σµ µ
µ
σ
0
C
⎤⎤
⎦
⎥
⎥
Recall from classical mechanics that a variation is defi ned such that variation at
the endpoints is 0, that is, at the initial and fi nal times
δ
µ
X = 0
.
In the case of the
endpoints of the string, we can apply either Neumann or Dirichlet boundary
conditions so we will have to handle each case differently (more on this as we go
along). For now, let’s take
δ
µ
X = 0
for simplicity. This means that we can throw
away the terms in the above expression which are integrals of total derivatives:
dPX d PX
i
f
τ
τ
δσ
σ
δ
τ
τ
µ
τµ
µ
σµ
∫∫
∂
∂
()
=
∂
∂
()
=00
0
This leaves us with
0
0
==
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
+
∫∫ ∫
δτσδ
τ
τ
τ
τ
µ
µ
τ
τ
τ
ST d d X
P
Tdd
i
f
i
f
C
σσδ
σ
τσδ
τ
µ
µ
σ
τ
τ
µ
µ
τ
0
0
C
C
∫
∫∫
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
=
∂
∂
X
P
TddX
P
i
f
++
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
P
µ
σ
σ
This gives us the equation of motion for the string, derived from the Nambu-Goto
action:
∂
∂
+
∂
∂
=
PP
µ
τ
µ
σ
τσ
0
(2.26)
