Методы безусловной многомерной оптимизации. Рекомендации к выполнению лабораторных, практических и курсовых работ по дисциплине Методы оптимизации
Подождите немного. Документ загружается.

21
"зацикливания". Проверяем условие окончания алгоритма, сравнивая длину
ребра симплекса с заданной точностью
2,02)68,328,3()15(
22
>=−−+−
.
Для продолжения поиска необходимо произвести редукцию последнего
симплекса.
Выбирается вершина, в которой функция принимает минимальное значе-
ние
x
(9)
= (1; 0,2). Две другие вершины будут расположены на серединах приле-
жащих к ней граней.
Таким образом, получился
новый симплекс с длиной ребра,
равной 1, и координатами
вершин:
Дальнейшие расчеты приведены в таблице:
№ точки x
1
x
2
y
x
(14)
x
(15)
0
0,5
0,2
1,07
0,68
2,46
зацикливание, уменьшаем ребро до 0,5
x
(14)
x
(16)
x
(17)
x
(18)
x
(19)
0
0,5
0,25
-0,25
-0,5
0,2
0,2
0,635
0,635
0,2
0,68
1,13
0,92
0,28
0,73
зацикливание, уменьшаем ребро до 0,25
x
(18)
x
(20)
x
(21)
-0,25
-0,375
-0,125
0,635
0,4175
0,4175
0,28
0,34
0,42
№ точки x
1
x
2
y
x
(22)
x
(23)
x
(24)
x
(25)
x
(26)
x
(27)
-0,50
-0,375
-0,625
-0,75
-0,875
-0,75
0,635
0,8525
0,8525
0,635
0,8525
1,07
0,15
0,25
0,074
0,146
0,022
0.1073
зацикливание, уменьшаем ребро до 0,125
x
(26)
x
(28)
x
(29)
x
(30)
x
(31)
-0,875
-0,75
-0,8125
-0,9375
-1
0,8525
0,8525
0,9612
0,9612
0,8525
0,022
0,032
0,024
0,0021
0,0435
Поскольку в послед-
ней точке произошло за-
цикливание, а длина ребра
симплекса 0,125 <
ε
=0,2,
условие окончания алго-
ритма выполняется.
Таким образом, за
точку минимума принима-
ем вершину симплекса, со-
ответствующую минимуму
целевой функции после его
зацикливания, т.е.
x*≈ x
(30)
= (-0,9375; 0,9612).
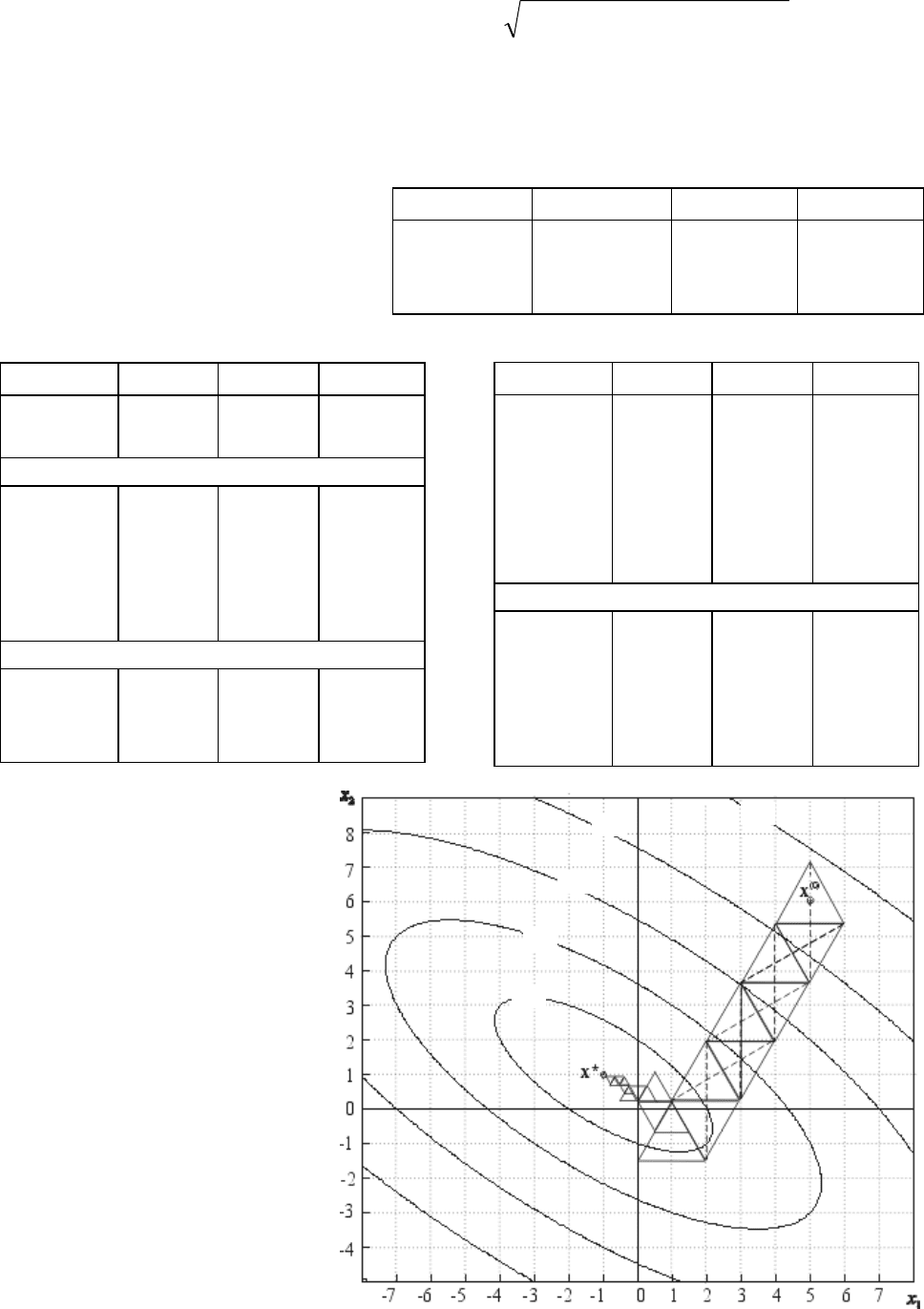
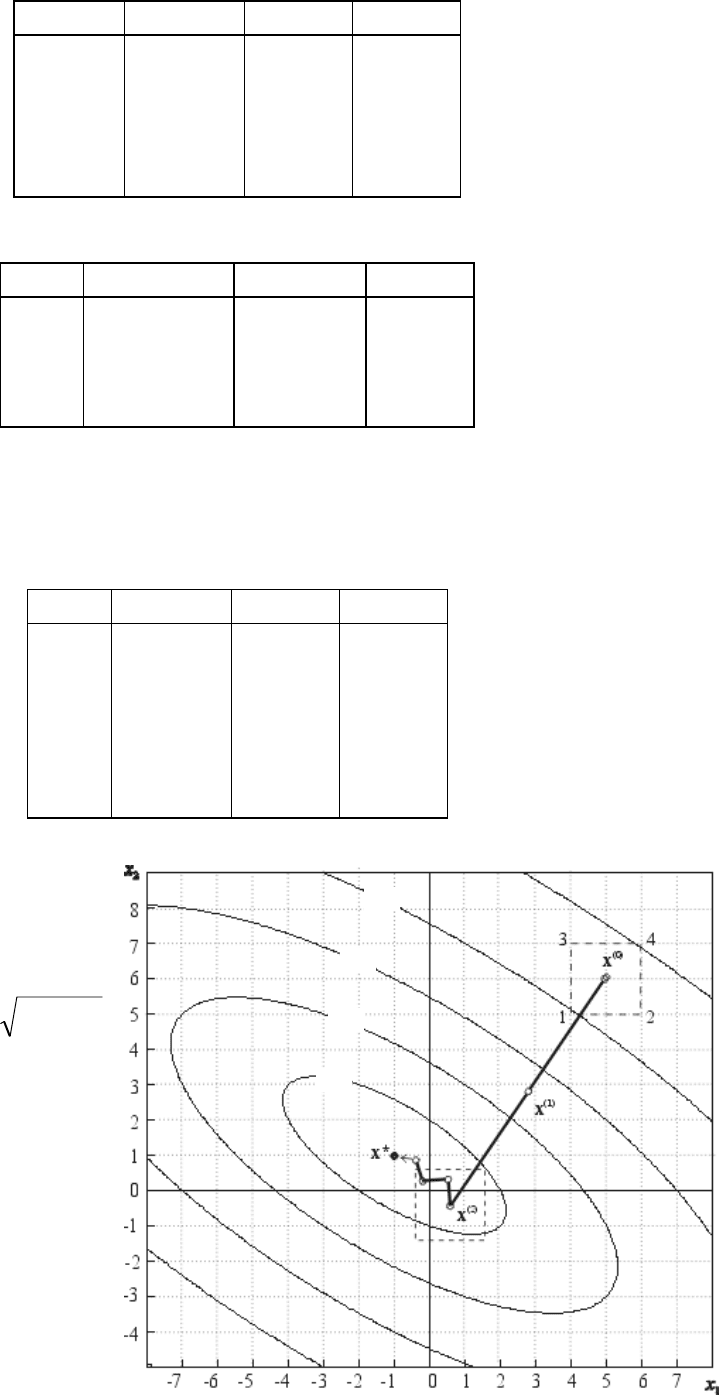
Траектория поиска
показана на рис.6.
Рис.6
№ точки x
1
x
2
y
x
(9)
x
(12)
x
(13)
1
1,5
0,5
0,2
-0,67
-0,67
2,08
3,48
2,82
5
20
50
100
200
22
6. Поиск экстремума методом Нельдера - Мида
В качестве начального
возьмем такой же симплекс, что
и в предыдущем примере.
“Наихудшей” вершиной
является
x
(3)
= (5; 7,16), а
“наилучшей” -
x
(1)
= (4; 5,42). После отражения имеем новый симплекс с
вершинами:
Поскольку отраженная
точка
x
(4)
является “наилучшей”,
производим растяжение
симплекса. Координаты новой
вершины рассчитываем по формулам: x
1
(5)
=2 x
1
(4)
– (x
1
(1)
+ x
1
(2)
)/2= 5 ;
x
2
(5)
= 2 x
2
(4)
- (x
2
(1)
+ x
2
(2)
)/2=1,94 .
Теперь " наихудшей" точкой будет вершина симплекса с координатами
x
(2)
= (6; 5,42). Дальнейшие расчеты приведены в таблице.
№ точки x1 x2 y
x
(1)
x
(2)
x
(5)
4
6
5
5,42
5,42
1,94
108,27
149,95
49,05
Производим отражение вершины x
(2)
x
(6)
3 1,94 25,28
Производим растяжение от вершины x
(6)
x
(7)
1,5 0,2 3,53
Производим отражение вершины x
(1)
x
(8)
2,5 -3,28 18,92
Производим отражение вершины x
(5)
x
(9)
-1 -5,02 72,48
Координаты последнего симплекса приведены в таблице:
Таким образом, вершина
x
(9)
оказалась "наихудшей". Для
продолжения поиска необ-
ходимо произвести редукцию
последнего симплекса.
Выбирается вершина, в которой функция принимает минимальное значе-
ние
x
(7)
= (1,5; 0,2). Две другие
вершины будут расположены
на серединах прилежащих к ней
граней.
Дальнейшие расчеты
приведены в таблице:
№ точки x
1
x
2
y
x
(1)
x
(2)
x
(3)
4
6
5
5,42
5,42
7,16
108,27
149,95
185,81
№ точки x
1
x
2
y
x
(1)
x
(2)
x
(4)
4
6
5
5,42
5,42
3,68
108,27
149,95
82,52
№ точки x
1
x
2
y
x
(7)
x
(8)
x
(9)
1,5
2,5
-1
0,2
-3,28
-5,02
3,53
18,92
72,48
№ точки x
1
x
2
y
x
(7)
x
(10)
x
(11)
1,5
2
0,25
0,2
-1,54
-2,41
3,53
6,66
16,29
№ точки x
1
x
2
y
Производим отражение вершины x
(11)
x
(12)
3,25 1,07 18,66
Производим редукцию относительно x
(7)
x
(7)
x
(13)
x
(14)
1,5
1,75
2,375
0,2
-0,67
0,635
3,53
3,96
9,19
Производим отражение вершины x
(14)
x
(15)
0,875 -1,105 4,48
23
Последняя точка является “лучшей”, по сравнению с отраженной, но тем
не менее, является “худшей” среди оставшихся, поэтому производим операцию
сжатия. Координаты новой вершины рассчитываем по формулам:
x
1
(16)
= 0,5x
1
(15)
+ (x
1
(7)
+ x
1
(13)
)/4 = 1,25 ;
x
2
(16)
=0,5x
2
(15)
+ (x
2
(7)
+ x
2
(13)
)/4 =-0,67.
Дальнейшие расчеты сведем в таблицу:
№ точки x
1
x
2
y
x
(7)
x
(13)
x
(16)
1,5
1,75
1,25
0,2
-0,67
-0,67
3,53
3,96
3,13
Производим отражение вершины x
(13)
x
(17)
1 0,2 2,08
Растяжение от вершины x
(17)
x
(18)
0,625 0,635 1,72
Отражение вершины x
(7)
x
(19)
0,375 -0,235 1,54
Растяжение ничего не дает, поэтому
производим отражение вершины x
(16)
x
(20)
-0,25 1,07 0,68
№ точки x
1
x
2
y
Отражение вершины x
(19)
x
(21)
-0,50 0,2 0,73
Отражение вершины x
(18)
x
(22)
-1,125 1,505 0,40
Отражение вершины x
(21)
x
(23)
-0,88 2,375 4,14
Редукция относительно x
(22)
x
(22)
x
(24)
x
(25)
-1,125
-1
-0,688
1,505
1,94
1,29
0,4
1,767
0,443
Отражение вершины x
(24)
x
(26)
-0,81 0,8525 0,023
Отражение вершины x
(25)
x
(27)
-1,25 1,07 0,037
Отражение вершины x
(22)
x
(28)
-0,938 0,418 0,61
Редукция относительно x
(26)
x
(26)
x
(29)
x
(30)
-0,81
-0,875
-1,03
0,8525
0,635
0,96
0,023
0,19
0,0064
Отражение вершины x
(29)
x
(31)
-0,969 1,18 0,076
В последней точке происходит выполнение условия окончания алгорит-
ма, т.е. среднеквадратичная величина разности значений функции в вершинах
симплекса и среднего ее
значения составляет
0,015<
ε
=0,2.
Таким образом, за
точку минимума прини-
маем вершину симплекса,
соответствующую мини-
муму целевой функции,
т.е.
x*≈ x
(30)
= (-1,03; 0,96).
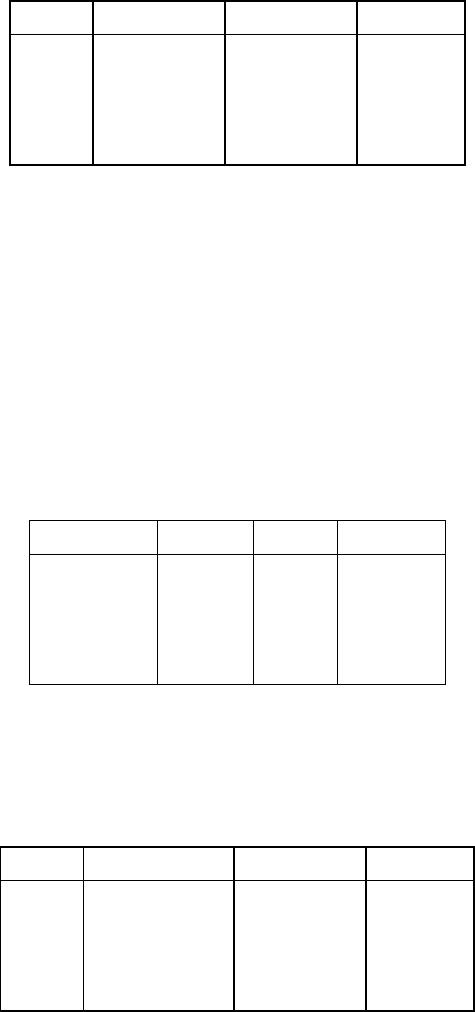
Траектория поиска
показана на рис.7.
Рис.7
5
20
50
100
24
7. Поиск экстремума методом крутого восхождения
Интервал варьирования для обeих переменных выбираем равным 1.
Реализуем ПФЭ 2
2
в точке x
(0)
= (5; 6), для чего рассчитываем
натуральные условия опытов.
Для первой переменной -1 будет соответствовать значение x
1
= 5-1·1= 4 ;
+1 будет соответствовать значение x
1
= 5+1·1= 6.
Для второй переменной -1 будет соответствовать значение x
2
= 6-1·1= 5 ;
+1 будет соответствовать значение x
2
= 6+1·1= 7.
Таким образом, матрица планирования будет иметь вид:
№ x
1
x
2
y
1
2
3
4
4
(-1)
6
(+1)
4
(-1)
6
(+1)
5
(-1)
5
(-1)
7
(+1)
7
(+1)
97
137
157
205
Исследуемую функцию аппроксимируем уравнением y= b
0
+ b
1
x
1
+ b
2
x
2
.
Рассчитываем коэффициенты уравнения регрессии:
b
1
= (-97+137-157+205)/4= 22 ; b
2
= (-97-137+157+205)/4= 32 .
Рассчитываем величину шага для x
1
и x
2
, принимая коэффициент
пропорциональности a=0,1 .
hx
1
= 0,1·1·22= 2,2 ; hx
2
= 0,1·1·32= 3,2 .
Начинаем движение по поверхности отклика в направлении градиента из
начальной точки (5; 6) с рассчитанным шагом.
Точки рассчитываются следующим образом:
x
1
(
k)
= 5- k·Δx
1
;
x
2
(
k)
= 6- k·Δx
2
, где k- номер шага.
В каждой новой точке рассчитываем значение функции.
№ точки x
1
x
2
y
x
(0)
x
(1)
x
(2)
x
(3)
5
2,8
0,6
-1,6
6
2,8
-0,4
-3,6
146,00
34,6
2
48,2
На третьем шаге значение функции увеличивается, следовательно, в
данном направлении минимальной точкой будет точка с координатами
[0,6; -0,4].
Так как заданная точность не достигнута, вновь реализуем ПФЭ 2
2
. Цен-
тром плана будет являться точка
x
(2)
=(0,6; -0,4).
№ x
1
x
2
y
1
2
3
4
-0,4
(-1)
1,6
(+1)
-0,4
(-1)
1,6
(+1)
-1,4
(-1)
-1,4
(-1)
-0,6
(+1)
-0,6
(+1)
9
5,8
0,2
5
Рассчитываем коэффициенты регрессии: b
1
=0,4 ; b
2
=-2,4 .
Рассчитываем значение шага для x
1
и x
2
.
hx
1
= 0,1·1 (0,4)= 0,04 ; hx
2
= 0,1·1·(-2,4)= -0,24 .
Начинаем движение по поверхности отклика.
25
№ точки x
1
x
2
y
x
(2)
x
(3)
x
(4)
x
(5)
x
(6)
0,60
0,56
0,52
0,48
0,44
-0,40
-0,16
0,08
0,32
0,56
2
1,51
1,21
1,10
1,19
В точке x
(5)
=(0,48; 0,32) значение функции минимально, принимаем эту
точку за исходную и вновь реализуем ПФЭ 2
2
.
№ x
1
x
2
y
1
2
3
4
-0,52
(-1)
1,48
(+1)
-0,52
(-1)
1,48
(+1)
-0,68
(-1)
-0,68
(-1)
-1,32
(+1)
-1,32 (+1)
4,26
3,46
0,74
7,94
Рассчитываем коэффициенты регрессии: b
1
=1,6 ; b
2
=0,24 .
Рассчитываем значение шага для x
1
и x
2
.
hx
1
= 0,1·1 (1,6)= 0,16 ; hx
2
= 0,1·1·(0,24)= 0,024 .
Начинаем движение по поверхности отклика.
Результаты расчета приведены в таблице:
№ x
1
x
2
y
x
(5)
x
(6)
x
(7)
x
(8)
x
(9)
x
(10)
0,48
0,32
0,16
0
-0,16
-0,32
0,32
0,296
0,272
0,248
0,224
0,2
1,10
0,87
0,72
0,63
0,61
0,65
В точке x
(9)
=(0,48; 0,32) значение функции минимально, принимаем эту
точку за исходную и вновь
реализуем ПФЭ 2
2
.
Процедуру повторяем
до тех пор, пока величина
вектора градиента
2
2
2
1
bb +
не станет меньше заданной
точности.
Траектория поиска
показана на рис.8.
Рис.8
5
20
50
100
26
ПРИЛОЖЕНИЕ 2
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ДЛЯ РУЧНОГО
РАСЧЕТА
Начальная точка
№
варианта
Вид целевой функции
f(x
1
,x
2
)
x
1
(0)
x
2
(0)
Точность
ε
1
(x
1
- 4x
2
)
2
+ (x
2
+ 5)
2
10 -5 0,15
2 (x
1
+ x
2
)
2
+ (x
2
+ 4)
2
9 5 0,3
3 (x
1
- 3x
2
)
2
+ (x
2
- 2)
2
4 10 0,25
4 (x
1
- 3x
2
)
2
+ (x
2
+ 1)
2
0 8 0,15
5 (x
1
+ 5x
2
)
2
+ (x
2
- 1)
2
8 10 0,35
6
(x
1
+ 2x
2
)
2
+ (x
2
- 3)
2
0 10 0,18
7 (x
1
- 2x
2
)
2
+ (x
2
- 3)
2
-7 -7 0,2
8 (x
1
+ x
2
)
2
+ (x
2
+ 2)
2
6 -1 0,18
9 (x
1
+ 3x
2
)
2
+ (x
2
+ 5)
2
10 10 0,35
10 (x
1
+ 9x
2
)
2
+ (x
2
- 1)
2
-6 5 0,25
11 (x
1
- 2x
2
)
2
+ (x
2
- 9)
2
15 12 0,15
12 (x
1
+ x
2
)
2
+ (x
2
+ 6)
2
10 8 0,18
13 (x
1
+ x
2
)
2
+ (x
2
- 1)
2
5 6 0,15
14 (x
1
- 2x
2
)
2
+ (x
2
- 3)
2
7 6 0,25
15 (x
1
+ 2x
2
)
2
+ (x
2
- 4)
2
-4 7 0,3
16
(x
1
- 2x
2
)
2
+ (x
2
+ 5)
2
-15 5 0,2
17 (x
1
- 6x
2
)
2
+ (x
2
+ 1)
2
-5 -3 0,2
18 (x
1
- 5x
2
)
2
+ (x
2
+ 6)
2
-10 -5 0,18
19 (x
1
+ 4x
2
)
2
+ (x
2
- 3)
2
-5 6 0,22
20 (x
1
+ 6x
2
)
2
+ (x
2
+ 2)
2
-10 7 0,22
21 (x
1
- 7x
2
)
2
+ (x
2
- 2)
2
8 6 0,3
22 (x
1
- 8x
2
)
2
+ (x
2
+ 1)
2
-5 -5 0,2
23 (x
1
- x
2
)
2
+ (x
2
- 7)
2
10 2 0,25
24 (x
1
+ 8x
2
)
2
+ (x
2
- 2)
2
-10 5 0,35
25 (x
1
- 5x
2
)
2
+ (x
2
+ 3)
2
-10 -5 0,21
27
ПРИЛОЖЕНИЕ 3
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ДЛЯ РАСЧЕТА
В ТАБЛИЧНОМ ПРОЦЕССОРЕ EXCEL
Начальная точка
№
вар.
Вид целевой функции
f(x
1
,x
2
)
x
1
(0)
x
2
(0)
Точность
ε
1
168
21
3
2
3
1
+−+ xxxx
5 10 0,1
2
)(
2
21
2
1
xxe
x
+
6 2 0,25
3
2121
2
2
2
1
63 xxxxxx −−++
-5 8 0,12
4
)(4
12
2
2
2
1
xxxx −++
9 5 0,13
5
1
2121
2
2
2
1
+−+++ xxxxxx
4 10 0,05
6
2018396
2121
2
2
3
1
++−−+ xxxxxx
15 18 0,1
7
2
21
2
2
2
1
)4()2()3( −−+−+− xxxx
8 10 0,05
8
6342
21
3
2
2
1
+−−+ xxxx
-5 7 0,2
9
2121
2
2
2
1
63 xxxxxx −−++
6 -1 0,08
10
8224
2121
2
2
2
1
+−−−+ xxxxxx
10 8 0,1
11
2
2
2
1
2
21
3
1
52 xxxxx ++−
0,5 -1,5 0,15
12
6)(42
12
2
2
2
1
+−++ xxxx
7 6 0,15
13
2121
2
2
2
1
63 xxxxxx −−++
-4 7 0,08
14
2121
2
2
2
1
44428 xxxxxx −+++
-5 -3 0,2
15
21
21
2050
xx
xx
++
10 -5 0,08
16
5)4(22
21
2
2
2
1
++++ xxxx
-5 6 0,12
17
21
2
2
2
1
ln18ln2 xxxx −−+
10 7 0,15
18
21
3
2
3
1
15 xxxx −+
8 6 0,13
19
2
21
4
1
)2()3( xxx −+−
10 10 0,05
20
⎟
⎠
⎞
⎜
⎝
⎛
−+
+−
1)(
)(
2
2
2
1
2
2
2
1
xx
exx
-5 -5 0,2
21
)0( 22252
122
2
1
2
2
2
1
4
1
>+−−+− xxxxxxx
8 12 0,25
22
)0( 22252
122
2
1
2
2
2
1
4
1
<+−−+− xxxxxxx
-10 5 0,35
23
)0(1222
122
2
1
2
2
4
1
>+−−+ xxxxxx
10 -5 0,1
24
)0( 1222
122
2
1
2
1
4
1
<+−−+ xxxxxx
-15 12 0,05
25
7643
21
2
2
2
1
+−++ xxxx
-6 5 0,15

28
ПРИЛОЖЕНИЕ 4
ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ВЫПОЛНЕНИЯ КУРСОВОЙ
РАБОТЫ
Координаты начальных
точек
задание 1 задание 2
№
вар.
Целевая функция
f(x
1
, x
2
)
x
1
x
2
x
1
x
2
Точность
ε
1 x
1
3
- 1,5x
1
2
- 18x
1
+ (3x
1
+ x
2
)
2
0 -20 10 -15 0,12
2 x
1
3
- 16,5x
1
2
+ (x
1
+ x
2
)
2
25 20 20 -30 0,15
3 x
1
3
- 7,5x
1
2
- 108x
1
+ (4x
1
+x
2
)
2
0 -70 20 5 0,05
4 x
1
3
+ 13,5x
1
2
- 66x
1
+ (5x
1
- x
2
)
2
25 -30 25 50 0,15
5 x
1
3
- 18x
1
2
+ 60x
1
+ (3x
1
+ x
2
)
2
5 75 15 -50 0,2
6 x
1
3
- 7,5x
1
2
+ 12x
1
+ (2x
1
- x
2
)
2
10 10 5 20 0,1
7 x
1
3
+ 4,5x
1
2
- 120x
1
+ (2x
1
- x
2
)
2
15 40 20 -20 0,08
8 x
1
3
- 18x
1
2
- 39x
1
+ (3x
1
- x
2
)
2
5 75 20 0 0,1
9 x
1
3
- 28,5x
1
2
+ 102x
1
+ (3x
1
+ x
2
)
2
25 0 0 -50 0,15
10 x
1
3
- 15x
1
2
- 288x
1
+ (4x
1
- x
2
)
2
30 -5 0 100 0,05
11 x
1
3
- 45x
1
2
+ 600x
1
+(x
1
+ x
2
)
2
50 -75 50 50 0,12
12 x
1
3
+ 9x
1
2
- 165x
1
+ (2x
1
- x
2
)
2
20 -30 5 50 0,15
13 x
1
3
- 36x
1
2
+ 240x
1
+ (2x
1
+ x
2
)
2
40 10 15 -100 0,13
14 x
1
3
- 34,5x
1
2
+ 126x
1
+ (3x
1
+ x
2
)
2
20 -150 35 20 0,12
15 x
1
3
- 75x
1
+ (3x
1
+ x
2
)
2
20 25 5 -75 0,06
16 x
1
3
- 9x
1
2
- 336x
1
+ (2x
1
- x
2
)
2
5 100 30 -30 0,08
17 x
1
3
- 6x
1
2
- 36x
1
+ (4x
1
-x
2
)
2
10 0 5 50 0,05
18 x
1
3
- 1,5x
1
2
- 6x
1
+ (3x
1
- x
2
)
2
6 12 3 20 0,15
19 x
1
3
- 40,5x
1
2
+ 216x
1
+ (2x
1
- x
2
)
2
40 -25 20 100 0,12
20 x
1
3
- 18x
1
2
- 324x
1
+ (3x
1
- x
2
)
2
10 100 30 -20 0,1
21 x
1
3
- 16,5x
1
2
- 378x
1
+ (4x
1
+ x
2
)
2
30 0 0 -100 0,3
22 x
1
3
- 13,5x
1
2
- 570x
1
+(2x
1
- x
2
)
2
30 -50 10 100 0,15
23 x
1
3
- 4,5x
1
2
- 462x
1
+ (3x
1
- x
2
)
2
40 -20 0 100 0,05
24 x
1
3
+ 9x
1
2
- 21x
1
+ (3x
1
- x
2
)
2
15 -15 0 30 0,1
25 x
1
3
- 6x
1
2
- 135x
1
+ (2x
1
- x
2
)
2
20 -20 25 35 0,04

29
ПРИЛОЖЕНИЕ 5
ВАРИАНТЫ ЗАДАНИЙ ДЛЯ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
1. )0(
0
4
1
2
2
2
1
32
2
32
1
>
⎩
⎨
⎧
=+
=+
x
xx
xx
2.
)0(
0
4
1
2
2
2
1
32
2
32
1
<
⎩
⎨
⎧
=+
=+
x
xx
xx
3.
)0(
02
01
1
2
2
2
2
1
12
>
⎩
⎨
⎧
=−+
=+−
x
xxx
xx
4.
)0(
01
0cos
1
2
2
2
1
211
>
⎩
⎨
⎧
=−+
=−
x
xx
xxx
5.
)0(
01
0cos
1
2
2
2
1
211
<
⎩
⎨
⎧
=−+
=−
x
xx
xxx
6.
)0(
0
12
2
32
12
2
2
2
1
>
⎩
⎨
⎧
=−
=+
x
xx
xx
7.
)0(
0
12
2
32
12
2
2
2
1
<
⎩
⎨
⎧
=+
=+
x
xx
xx
8.
)0(
01
0sin
1
2
2
2
1
12
>
⎩
⎨
⎧
=−+
=−
x
xx
xx
9.
)0(
01
0sin
1
2
2
2
1
12
<
⎩
⎨
⎧
=−+
=−
x
xx
xx
10.
)0(
0
02
1
2
2
2
2
2
1
1
<
⎩
⎨
⎧
=−
=−+
−
x
ex
xxx
x
11.
)0(
0
02
1
2
2
2
2
2
1
1
>
⎩
⎨
⎧
=−
=−+
−
x
ex
xxx
x
12. )0(
01
0122
1
12
2
2
21
2
1
>
⎩
⎨
⎧
=+−
=+−+−
x
xx
xxxx
13.
)0(
0ln
02
2
12
1
2
2
2
1
>
⎩
⎨
⎧
=−
=−+
x
xx
xxx
14.
)0(
11
0122
1
12
2
2
21
2
1
>
⎩
⎨
⎧
−=+−
=++++
x
xx
xxxx
15.
)0(
02
1
2
1
2
2
2
1
32
2
32
1
>
⎩
⎨
⎧
=−+
=+
x
xxx
xx
16.
)0(
02
1
2
1
2
2
2
1
32
2
32
1
<
⎩
⎨
⎧
=−+
=+
x
xxx
xx
17.
)0(
01
0sin
1
2
2
2
1
211
>
⎩
⎨
⎧
=−+
=−
x
xx
xxx
18.
)0(
01
0sin
1
2
2
2
1
211
<
⎩
⎨
⎧
=−+
=−
x
xx
xxx
19.
)0(
01
0
1
1
2
2
2
1
2
2
1
1
>
⎪
⎩
⎪
⎨
⎧
=−+
=−
+
x
xx
x
x
x
20.
)0(
01
0
1
1
2
2
2
1
2
2
1
1
<
⎪
⎩
⎪
⎨
⎧
=−+
=−
+
x
xx
x
x
x
21.
)0(
0)1ln(
2
1
02
1
12
2
2
2
2
1
>
⎪
⎩
⎪
⎨
⎧
=+−
=−+
x
xx
xxx
22.
)0(
0)1ln(2
02
1
12
2
2
2
2
1
>
⎩
⎨
⎧
=+−
=−+
x
xx
xxx
23.
)0(
01
02
1
2
2
2
1
12
1
>
⎩
⎨
⎧
=−+
=−
−
x
xx
exx
x
30
24.
)0(
01
02
1
2
2
2
1
12
1
<
⎩
⎨
⎧
=−+
=−
−
x
xx
exx
x
25.
(
)
⎪
⎩
⎪
⎨
⎧
>=−+
>−=+
)001
,0()(2
22
2
1
1
2
2
2
1
2
2
2
2
1
xxx
xxxxx
Рекомендуемая литература
1. Базара М., Шетти К. Нелинейное программирование. Теория и алгорит-
мы. -М.: Мир, 1982.
2.
Банди. Методы оптимизации. -М.: Радио и связь, 1988.
3.
Васильев Ф. П. Численные методы решения экстремальных задач. -
М.:Наука, 1981.
4.
Кафаpов В.В. Методы кибеpнетики в химии и химической технологии.
М.: Химия, 1985.
5.
Курицкий Б. Поиск оптимальных решений средствами Excel 7.0 :BHV-
Спб., 1997.
6.
Моисеев Н. Н., Иванилов Ю. П., Столярова Е. М. Методы оптимизации. -
М.: Наука, 1975.
7.
Мочалов С.П. Методы оптимизации металлургических процессов. Учеб.
пособие. – Кемерово: КузПИ, 1989.
8.
Поляк Б. Т. Введение в оптимизацию. -М.: Наука, 1983.
9.
Реклейтис Г., Рейвиндран А., Рэгсделк. Оптимизация в технике. В 2-х кн.
-М.: Мир, 1986.
10.
Рыков А.С. Поисковая оптимизация. Методы деформируемых конфигу-
раций. -М.: Наука, 1993.
11.
Химмельблау Д. Прикладное нелинейное программирование. -М.: Мир,
1974.
12.
Циpлин А.М. Оптимальное упpавление технологическими пpоцессами.
М.: Энеpгоатомиздат, 1986.
