Михальчук В.М., Михальчук А.В. Линейный регрессионный анализ результатов химического эксперимента в системе STATISTICA

Подождите немного. Документ загружается.

Рис.30 Таблица с корреляционной матрицей для выбранных переменных.

Визуально корреляцию между всеми переменными можно оценить по

двумерным графическим зависимостям между всеми переменными. Для по-

строения этих графиков нажмите на кнопку

Matrix plot of correlations, которая

расположена на вкладке

Advanced. При этом откроется окно Select Variables

(рис.31), в котором выберите все переменные Y, X1, X2. После нажатия на

кнопку

OK на экран монитора выводятся матричные графики – диаграммы рас-

сеяния, которые можно считать графическим эквивалентом корреляционной

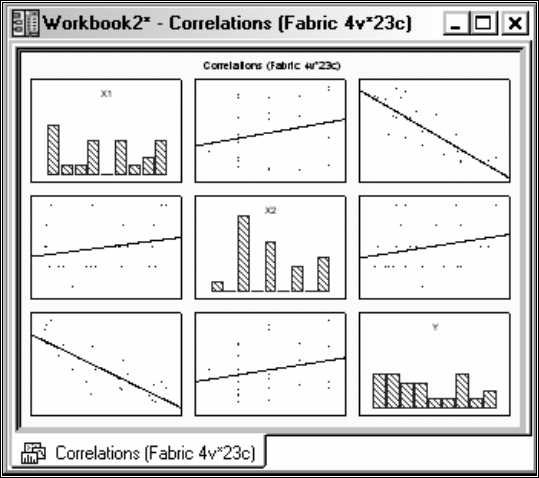
матрицы (рис.32). На матричном графике этого типа изображаются двумерные

диаграммы рассеяния, организованные в форме матрицы (значения переменной

по столбцу используются в качестве координат X, а значения переменной по

строке - в качестве координат Y). Гистограммы, изображающие

распределение

каждой переменной, располагаются на диагонали матрицы (в случае квадрат-

ных матриц) или по краям (в случае прямоугольных матриц).

Рис.31 Окно выбора переменных для построения матричных графиков.

Для рассматриваемого примера

Surface коэффициент корреляции между

независимыми переменными

X1 и X2 составляет 0,222103. Следовательно, эти

величины слабо коррелированны и для дальнейшего анализа может быть ис-

пользован стандартный метод наименьших квадратов, с включением в модель

всех независимых переменных. Из практики установлено, что при проведении

множественного линейного регрессионного анализа стандартным методом

наименьших квадратов коэффициент линейной корреляции между независи-

мыми переменными не должен превышать 0,8.

Рис.32 Матричные графики.

2.3 Оценка адекватности модели и параметров уравнения регрессии

Для продолжения регрессионного анализа с использованием стандартно-

го метода наименьших квадратов достаточно нажать кнопку

OK в окне Review

descriptive statistics

. При этом, как и в случае однофакторной модели, откроет-

ся окно

Multiple Regression Results (рис.33), в котором приведены все резуль-

таты анализа.

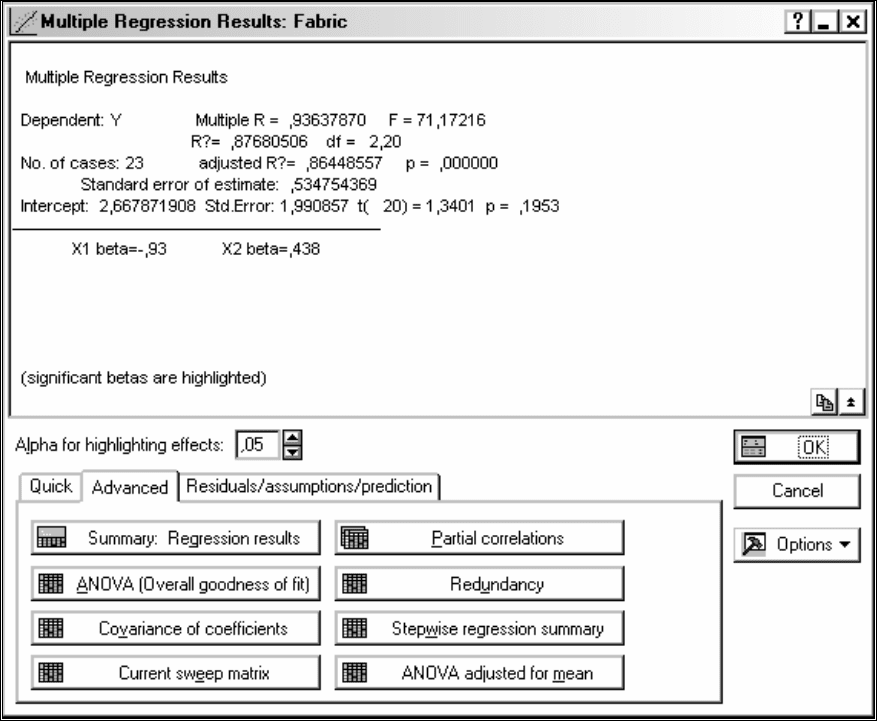
Как следует из значений множественного коэффициента корреляции и

детерминации, выбранная линейная модель с двумя факторами

X1 и X2 адек-

ватно описывает экспериментальные данные, и вариация зависимой перемен-

ной на 88 % может быть объяснена вариацией независимых переменных. F-

критерий проверки значимости линейной модели регрессии имеет высокие зна-

чения (

F = 71,17216). При числе степеней свободы 2 и 20 гипотеза о равенстве

нулю параметров уравнения регрессии (H

: b

= b

= … = b

= 0, b

≠ 0) может

быть отвергнута с вероятностью совершить ошибку первого рода меньше

0,0001 % (

p-level < 0,000001). В данном случае первое число степеней свободы

соответствует количеству независимых переменных в модели, а второе число

степеней свободы – число наблюдений за вычетом количества параметров

уравнения регрессии: n – 3). Следует напомнить, что детальные результаты

проверки данной гипотезы приведены в таблице

Analysis of Variance, которая

может быть открыта нажатием на кнопку

ANOVA (Overall goodness of fit) на

вкладке

Advanced окна Multiple Regression Results.

Рис.33 Окно результатов анализа (вкладка

Advanced).

При рассмотрении результатов многофакторного регрессионного анализа

необходимо обратить внимание на значения регрессионных бета-

коэффициентов – коэффициенты регрессии, которые были бы получены, если

бы мы заранее стандартизовали все переменные, т.е. сделали их среднее рав-

ным 0, а стандартное отклонение равным 1. Одно из преимуществ бета-

коэффициентов (по сравнению с b-коэффициентами) заключается в

том, что

бета-коэффициенты позволяют сравнить относительные вклады каждой неза-

висимой переменной в предсказание зависимой переменной. Значения бета-

коэффициентов приведены в средней части окна

Multiple Regression Results и

здесь статистически значимые коэффициенты выделены красным цветом. Бе-

та-коэффициенты приведены также в таблице

Regression Summary for

Dependent Variable, которая может быть вызвана нажатием на кнопку

Summary: Regression results (в этом же окне).

В примере

Surface бета-коэффициенты для переменных X1 и X2 соот-

ветственно равны -0,930707 и 0,437622 (рис.33). Следовательно, переменная

вносит больший вклад в изменение зависимой переменной.

Полный коэффициент парной корреляции между зависимой переменной

Y и фактором X2 имеет низкое значение R = 0,230910 (см. таблицу Correla-

tions

, рис.30). Для случая однофакторной корреляции такое значение было бы

статистически не значимо, поскольку при числе наблюдений n = 23, числе сте-

пеней свободы f = 21, уровне значимости p = 0,05 выполняется неравенство

)],(/)2(1[

−

−+< pftnR

(0,05332 < 0,07573). При этом гипотезу о равенстве

нулю истинного значения коэффициента парной корреляции (0:

H ), без-

условно, следует признать согласующейся с полученными экспериментальны-

ми данными.

2.4 Частные коэффициенты корреляции и толерантность

Применение полных коэффициентов парной корреляции при множест-

венной корреляции для изучения связи двух величин может привести к непра-

вильным выводам. В данном случае необходимо анализировать частные коэф-

фициенты корреляции, которые отражают степень линейной взаимосвязи

между двумя переменными, вычисленную после устранения влияния всех дру-

гих переменных. Так, если предполагается, что изменение величин

и z

опре-

деляется в какой-то мере изменением остальных величин z

, …, z

, то показате-

лем линейной связи между z

и z

при исключении влияния z

, …, z

является

частный коэффициент корреляции, который определяется как обычный коэф-

фициент корреляции между

∗

−

zz и

∗

−

zz , где

∗

z и

∗

z – соответственно наи-

лучшие линейные приближения z

и z

по z

, …, z

. Частный коэффициент кор-

реляции выражается через элементы корреляционной матрицы и для случая

n = 3 он равен

13231312231

)]1)(1)[((

−

⋅

−−−=

ρρρρρρ

Если между двумя величинами частный коэффициент корреляции стано-

вится близким к нулю или уменьшается по сравнению с полным парным коэф-

фициентом корреляции, то можно сказать, что взаимосвязь этих величин опре-

деляющим образом (или в значительной мере) имеет место благодаря третьим

факторам. Если же при фиксировании третьих факторов степень взаимозависи-

мости

двух величин возрастает (частный коэффициент корреляции увеличива-

ется), то это означает, что эти факторы маскировали истинную взаимосвязь

двух величин.

Частные коэффициенты корреляции приведены в таблице

Variables cur-

rently in

the Equation (Рис.34), которая вызывается нажатием на кнопку Partial

correlation

в окне Multiple Regression Results (на вкладке Advanced). Част-

ные коэффициенты корреляции и толерантность приведены также в таблице

Redundancy of Independents Variables (Рис.35), которая вызывается кнопкой

Redundancy на этой же вкладке.

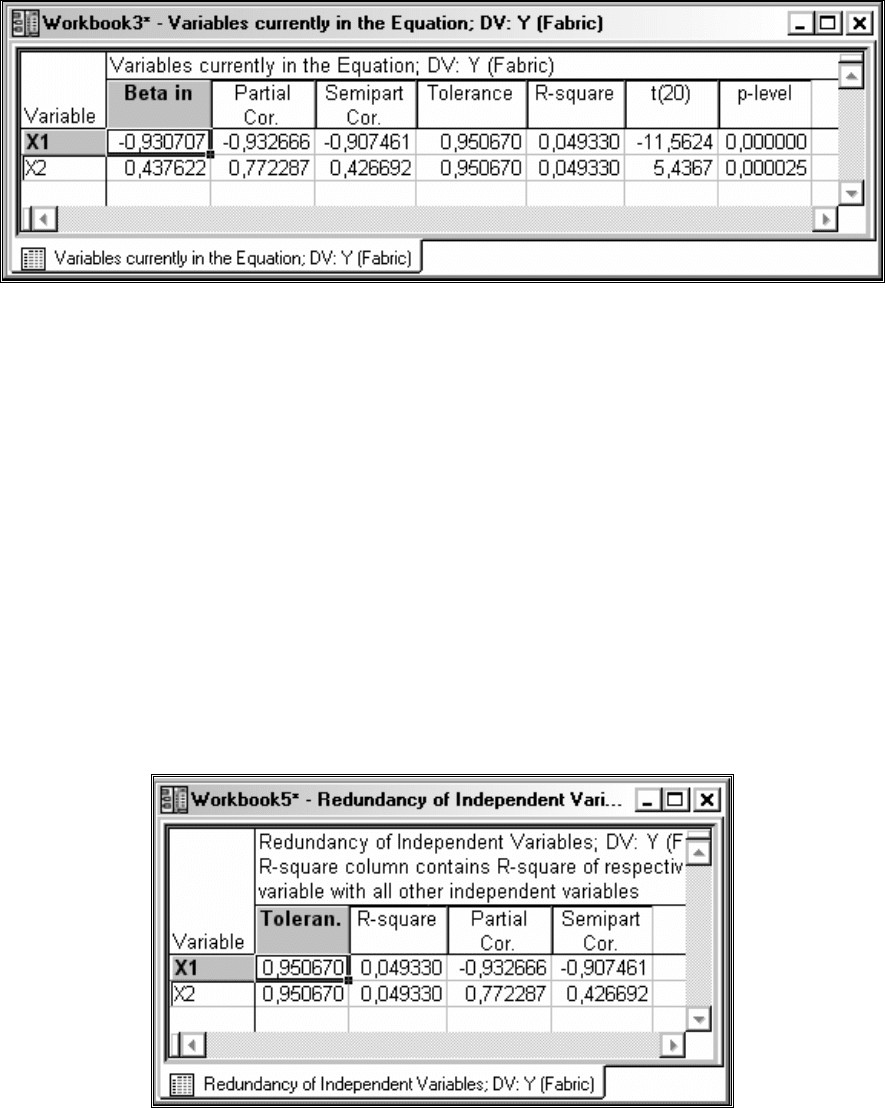
Рис.34 Частные коэффициенты корреляции и толерантность для примера

Surface.

Нажмите на кнопку

Partial correlation и сравните полученные значения

частных и полных коэффициентов корреляции. Как видно из таблиц

Variables

currently in

the Equation (рис.34) и Correlations (рис.30) при исключении пе-

ременной

X2 коэффициент корреляции между зависимой переменной Y и неза-

висимой переменной

X1 заметно повышается: полный и частный коэффициен-

ты корреляции соответственно равны –0,8335 и –0,9327. Еще больше

увеличивается степень взаимосвязи между зависимой переменной

Y и незави-

симой переменной

X2 при исключении влияния переменной X1: полный и ча-

стный коэффициент корреляции соответственно равны 0,2309 и 0,7723. Это оз-

начает, что оба фактора и, особенно,

X1 маскировали истинную взаимосвязь

исследуемых переменных.

Рис.35 Частные коэффициенты корреляции и толерантность для примера

Surface.

Толерантность переменной в множественной регрессии определяется как

(

⋅

−

R ), где

⋅i

R – квадрат коэффициента множественной корреляции i-той пе-

ременной со всеми остальными независимыми переменными, входящими в

уравнение регрессии. Поэтому, чем меньше толерантность переменной, тем бо-

лее избыточен ее вклад в уравнение регрессии (т.е. тем более ее вклад избыто-

чен при заданных значениях других переменных). Если толерантность любой

переменной в уравнении регрессии равна нулю (или очень близка к нулю), оце-

нивание уравнения регрессии невозможно.

Как видно из таблицы

Variables currently in the Equation (рис.34), в

примере

Surface квадрат коэффициента корреляции

⋅i

для независимых пе-

ременных

X1 и X2 составляет 0,049330, а толерантность 0,950670. Следова-

тельно, вклад в уравнение регрессии этих переменных не может рассматривать-

ся как избыточный. В этой же таблице приведены t-статистики и уровни

значимости, с которой может быть отвергнута (принята) гипотеза о равенстве

нулю параметров b

и b

уравнения регрессии.

Оценка значимости параметров уравнения регрессии также может быть

проведена по результатам анализа, приведенным в таблице

Regression sum-

mary for Dependent Variable

. Следует напомнить, что эта таблица может быть

открыта при нажатии на кнопку

Summary: Regression results (вкладки Quick

или

Advanced, рис.6). В колонке B данной таблицы приведены оценочные зна-

чения b-коэффициентов уравнения регрессии, а в колонках

St. Err. of B, t(20) и

p-level соответственно значения стандартной ошибки для b-коэффициентов, их

t-статистики и уровень значимости.

Рис.36 Краткие результаты регрессии для примера

Surface.

В рассматриваемом примере t-статистика для свободного члена (

b ) име-

ет низкое значение (1,3401) и при числе степеней свободы f = 20 уровень зна-

чимости составляет 0,195252. В этом случае гипотеза о равенстве нулю свобод-

ного члена уравнения регрессии (H

: b

= 0) не может быть отвергнута,

поскольку вероятность совершить ошибку первого рода составляет

~20 %. Сле-

довательно, оценочное значение

= 2,667872 статистически не значимо (при

этом строка

Intercept в таблице Regression summary for Dependent Variable

не выделяется шрифтом красного цвета).

Оценочное значение параметра

b равно -0,079833, а его стандартная

ошибка составляет 0,006905. При числе степеней свободы 20 (указывается в

скобках:

t(20)) значении t-статистики равно 28,76, а уровень значимости не пре-

вышает 0,000001. В этом случае нуль-гипотеза о равенстве нулю истинного

значения параметра при

X1 в уравнении регрессии (H

: b

= 0) может быть от-

вергнута с вероятностью совершить ошибку первого рода < 0,0001 %. Это сви-

детельствует о статистической значимости оценочного значения параметра

b .

Аналогично параметр

b при переменной

X2 в уравнении регрессии равен

0,527105, его стандартная ошибка составляет 0,096954, t-статистика равна

5,4367, а уровень значимости – 0,000025. При таком уровне значимости нуль-

гипотеза о равенстве нулю истинного значения параметра b

уравнения регрес-

сии (H

: b

= 0) может быть отвергнута с вероятностью совершить ошибку пер-

вого рода 0,0025 %. Следовательно, и параметр уравнения

b при переменной

X2 статистически значим.

2.5 Анализ остатков

Для проведения анализа остатков, как и при проведении однофакторного

анализа, необходимо открыть вкладку

Residualss/assumption/prediction и на-

жать кнопку

Perform Residuals Analysis в окне Multiply Regression Result.

При этом откроется окно

Residuals Analysis, в верхнем поле которого продуб-

лированы основные результаты регрессионного анализа. Ниже расположен ряд

вкладок с кнопками для вызова таблиц и графиков с результатами анализа ос-

татков. В частности, эти результаты сведены в таблицу

Predicted & Residuals

Value

. Для того чтобы вызвать данную таблицу необходимо открыть вкладку

Quick или Advanced и нажать на кнопку Summary: Residuals & Predicted,

либо нажать на кнопку

Summary в окне Residuals Analysis. В нижней части

таблицы приведены максимальные, минимальные, средние значения, а также

медианы для всех указанных выше величин.

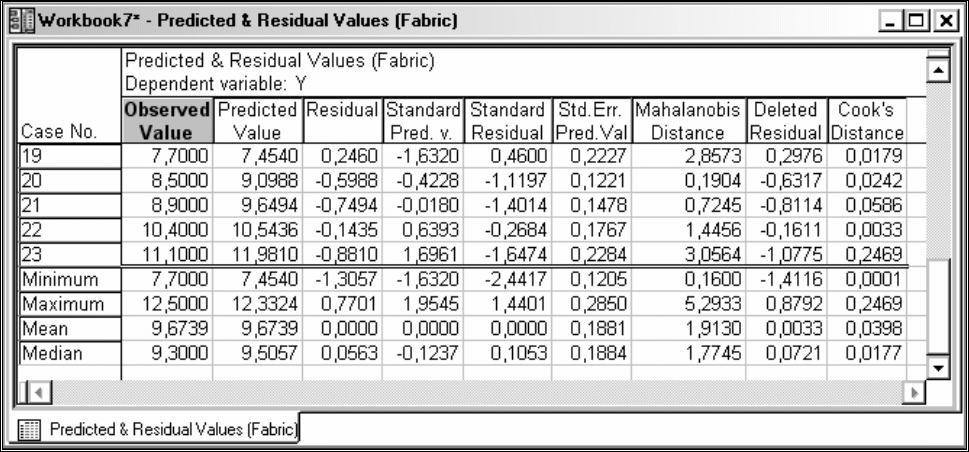
Из таблицы

Predicted & Residuals Value (рис.37) видно, что для примера

Surface среднее значение остатков имеет очень маленькое значение (≈4⋅10

-8

Рис.37 Таблица остатков для примера Surface.