Мосин В.Г. Математические основы компьютерной графики: Монография

Подождите немного. Документ загружается.

5.2. Производные 131

5.2.5 Производные высших порядков

В данном разделе мы рассмотрим вопросы последовательного дифференци-

рования функции и, тем самым, обобщим понятия непрерывности и гладко-

сти функций понятием их бесконечной дифференцируемости (см. опр. 59,

стр. 131)

Определение 58 (производные высших порядков) Допустим, функ-

ция f(x) дифференцируема на отрезке [a, b], то есть — на отрезке [a, b] опре-

делена функция f



(x). Может оказаться так, точ функция f



(x) снова будет

дифференцируемой на [a, b]. В этом случае ее производная называется вто-

рой производной функции f(x):



(x)=





(x)





Аналогично определяются производные третьего и более высоких

поряд-

ков:



(x)=





(x)





, ит.д. f

(n)



(n−1)

(x)





Пример 83 Будем последовательно дифференцировать многочлен:

f(x)=x

+2x, f



(x)=3x

+2,f



(x)=6x, f



(x)=6,f



(x)=0.

Мы видим, что, начиная с производной четвертого порядка, все остальные про-

изводные оказываются равными нулю, то есть — существуют. Таким образом, мы

можем заключить, что полиномальные функции являются бесконечно дифферен-

цируемыми.

Пример 84 Будем последовательно дифференцировать логарифмическую функ-

цию:

f(x)=lnx, f



(x)=



(x)=−



(x)=2



(x)=1· 2 · 3

Полученный ряд производных позволяет сделать вывод о существовании произ-

водной любого порядка от логарифмической функции, причем

(n)

(x)=(−1)

n−1

(n −1)!

Таким образом, мы можем заключить, что логарифмические функции также яв-

ляются бесконечно дифференцируемыми.

Определение 59 (класс C

∞

) О бесконечно дифференцируемых функци-

ях говорят, что они образуют класс функций C

∞

Пример 85 Нетрудно убедиться, что a

, sin x, cos x ∈ C

∞

Порядок производной заключается в скобки, чтобы отличать n-ю производную функ-

ции от ее n-й алгебраической степени.

132 Глава 5. Математический анализ

5.2.6 Производные функций, заданных параметриче-

ски

Определение 60 (производная параметрической функции) Пусть

имеется функция, заданная параметрически при помощи параметра u:

p(u)=



(u)



; u ∈ [α

; α

] .

Пусть функции p

(u) и p

(u) являются дифференцируемыми на отрезке

[α

; α

] как функции переменной u. Тогда производной параметрически за-

данной функции p(u) называется праметрически заданная функция p



(u),

определенная следующим образом



(u)=





(u)



(u)



; u ∈ [α

; α

]

Таким образом, дифференцирование функций, заданных параметрически,

сводится в дифференцированию явных функций.

Пример 86 Вычислить производную функции, заданной параметрически:

p(u)=



sin 2u

u cos u



Согласно определению (см. опр. 60, стр. 132), нам достаточно по отдельно-

сти продифференцировать координаты функции p(u):



(u) = (sin 2u))



=2cos2u,



(u)=



u cos u





= u



· cos u + u · (cos u)



=1· cos u + u · (−sin u) = cos u − u sin u.

Таким образом, производная данной параметрически заданной функции —

это следующий вектор:



(u)=



2cos2u

cos u − u sin u



Пример 87 Вычислить значение производной функции p(u), заданной па-

раметрически, при указанном значении параметра u:

p(u)=







1+u







при u =2.

В большинстве учебников принято другое определение производной функции, задан-

ной параметрически. Такая функция связывает независимые переменные x и y опосре-

довано через параметр u, и обычно под производной такой функции понимают именно

производную функции y по переменной x. Особенность нашего определения состоит в

том, что мы дифференцируем функцию по параметру u, а не по одной из переменных.

5.3. Геометрический смысл производной 133

Прежде всего, вычислим функцию, являющуюся производной функции p(u).

Для этого (так же, как и выше) продифференцируем ее координаты.



(u)=



1+u





(3u)



· (1 + u

) − 3u · (1 + u

)



(1 + u

)

3 · (1 + u

) − 3u · (0 + 2u)

(1 + u

)

1 − u

(1 + u

)



(u)=



1+u





(3u

)



· (1 + u

) − 3u

· (1 + u

)



(1 + u

)

6u · (1 + u

) − 3u

· (0 + 2u)

(1 + u

)

(1 + u

)

Таким образом, производная функции p(u) — это следующая парметриче-

ски заданная функция:



(u)=







1 − u

(1 + u

)

(1 + u

)







, при этом



(2) = −



(2) =

Следовательно, искомое значение производной (при u =2) — это вектор с

числовыми координатами −9/25 и 12/25:



(2) = (−9/25; 12/25) .

5.3 Геометрический смысл производной

В этом разделе мы выясним геометрический смысл производной функции

в точке (см. теор. 76, стр. 133) и, тем самым, получим инструмент для

описания касательных к графикам явных функций (см. теор. 77, стр. 134).

Несмотря на то, что в пиложениях нам понадобятся парметрические функ-

ции (см. главу 6, стр. 139), мы начинаем с явных функций: действия с

парметрическими функциями во много повторяют действия с явными.

Практические задачи, относящиеся к этому разделу, представлены в при-

ложениях (см. приложение C.2, стр. 213).

Определение 61 (касательная к кривой) Пусть M — точка, лежащая

на непрерывной кривой C.ПустьMM



— секущая к кривой C, проходящая

через точки M и M



. Касательной к кривой C, проведенной в точке M ,на-

зывается предельное положение секущей MM



, когда точка M



бесконечно

приближается по кривой C к точке M .

5.3.1 Геометрический смысл производной явной функ-

ции

Теорема 76 (геометрический смысл производной) Пусть явная функ-

ция y = f(x) обладает производной f



) в точке x

. Тогда ее график

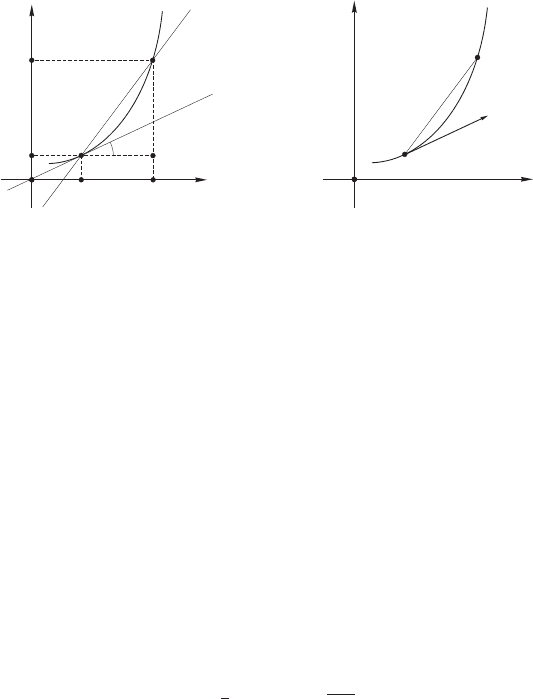
134 Глава 5. Математический анализ



+∆x

+∆y

(a) Явная функция.

p(u

)

p(u

+∆u)



)

(b) Параметрическая функция.

Рис. 5.3: Геометрический смысл производной.

обладает касательной в точке (x

,f(x

)), причем

tg ϕ = f



) ,

где ϕ — угол наклона касательной к положительному направлению гори-

зонтальной оси.

Доказательство Возьмем на графике функции точку M(x

,f(x

)).Пусть

переменная x получает в точке x

приращение ∆x. Возьмем на графике еще

одну точку M



+∆x, y

+∆y) и проведем секущую MM



Теперь мы можем рассмотреть прямоугольный треугольник MNM



с кате-

тами MN =∆x и M



N =∆y (cм. рис. 5.3, стр. 134). Тангенс угла наклона

секущей MM



вычисляется, исходя из тригонометрических из соотношений

в треугольнике MNM



(как отношение длины противолежащего катета к

длине прилежащего):





MN =

∆y

∆x

Пусть теперь точка M



стремится вдоль кривой к точке M. Тогда, очевидно,

∆x → 0 и секущая стремится к своему предельному положению, то есть —

к касательной. Отсюда, пользуясь определениями (см. опр. 53, 61, стр. 117,

133), получим:

tg ϕ = f



) .

Теорема доказана.

Пример 88 Найдем тангенсы углов наклона касательной к кривой y = x

в точ-

ках M

(1/2, 1/4) и M

(−1, 1). Производная функции вычисляется элементарно:



=2x.

Поэтому (см. теор. 76, стр. 133):

tg ϕ

= y



(1/2) = 1 , tg ϕ

= y



(−1) = −2 .

Теорема 77 (уравнение касательной) Пусть явная функция f (x) обла-

дает производной в точке x

. Тогда ее график обладает касательной l в

точке x

, причем:

l : y = f (x

)+f



)(x − x

) .

5.3. Геометрический смысл производной 135

Доказательство Пусть касательная l к графику функции y = f(x) имеет

уравнение

l : y = kx + b.

Тогда, в силу теоремы о геометрическом смысле производной (см. теор. 76,

стр. 133), имеем k = f



). Поэтому

l : y = f



)x + b.

Кроме того, известно, что прямая l проходит через точку (x

,f(x

)).Сле-

довательно,

f(x

)=f



+ b, откуда b = f(x

) − f



Используя найденные значения для k и b, окончательно получим:

l : y = f



)x+ f (x

)−f



, то есть l : y = f (x

)+f



)(x−x

) .

Теорема доказана.

Пример 89 Запишем уравнения касательных к графику функции y =sinx в

точках x

= π/2 и x

= π. Для этого нам необходимо знать значения функции в

точках и значения ее производной:

y(π/2) = sin(π/2) = 1 ,y(π)=sin(π)=0,



(π/2) = cos π/2=0,y



(π)=cos(π)=−1 .

Поэтому (см. теор. 77, стр. 134):

: y =1,l

: y = π − x.

5.3.2 Геометрический смысл производной функции, за-

данной параметрически

Теорема 78 (геометрический смысл производной) Пусть кривая p(u)

описывается параметрически:

p(u)=



(u)



Тогда вектор производной этой функции, вычисленный при значении пара-

метра u = u







)



)



— это в точности вектор, касательный к кривой p(u), проведенный к ней в

точке p(u

Доказательство Зафиксируем значение параметра u = u

и придадим

ему приращение ∆u (см. рис. 5.3, стр. 134). Тогда точка кривой M = p(u

)

перейдет в точку M



= p(u

+∆u). Координаты вектора M



M таковы:



M =



+∆u)



−



)





+∆u) − p

)

+∆u) − p

)





∆p



136 Глава 5. Математический анализ

Это вектор, который является секущим вектором кривой p(u) в точке p(u

Если точка M



бесконечно приближается к точке M вдоль кривой, то вектор



M бесконечно приближается в касательному положению (см. опр. 61,

стр. 133). Разделим вектор M



M на ∆u и перейдем к пределу:

lim

∆u→0

∆u



∆p



= lim

∆u→0







∆p

∆u

∆p

∆u













lim

∆u→0

∆p

∆u

lim

∆u→0

∆p

∆u











)



)



Теорема доказана.

Пример 90 Вычислить касательный вектор к кривой

p(u)=



− 2u

+ u − 4



в точке, отвечающей значению параметра u

=2. Применим теорему о геомет-

рическом смысле производной функции, заданной параметрически (см. теор. 78,

стр. 135). Согласно ей, искомый касательный вектор — это p



(2):



(u)=



− 4u

6u +1



, поэтому p



(2) =



3 ·2

− 4 · 2

6 ·2+1







Аналогично тому, как мы выше описывали уравнения касательных к гра-

фикам явных функций, мы можем описать и касательные к параметрически

заданным кривым при помощи их производных. Для этого нам понадобят-

ся некоторые знания о том, как описываются прямые. Их явные уравнения

вида y = kx+b — это не единственный способ их описать. Нам будет удобнее

работать не с явными, а с каноническими уравнениями прямых.

Теорема 79 (каноническое уравнение прямой) Пусть прямая l про-

ходит через точку A(x

) параллельно вектору a = {a

}.Тогдаее

уравнение может быть записано в канонической форме следующим обра-

зом:

l :

x − x

y − y

Доказательство Возьмем на прямой l переменную точку M с координа-

тами (x, y). Тогда вектор AM с координатами {x −x

,y−y

}, лежащий на

прямой l, по условию теоремы, должен быть параллелен вектору a. Парал-

лельность же векторов означает пропорциональность их координат:

x − x

y − y

Теорема доказана.

Теорема 80 (уравнение касательной) Касательная к кривой p(u), опи-

санной параметрически

p(u)=



(u)



в точке, отвечающей значению параметра u = u

, имеет следующее кано-

ническое уравнение:

x − p

)



)

y − p

)



)

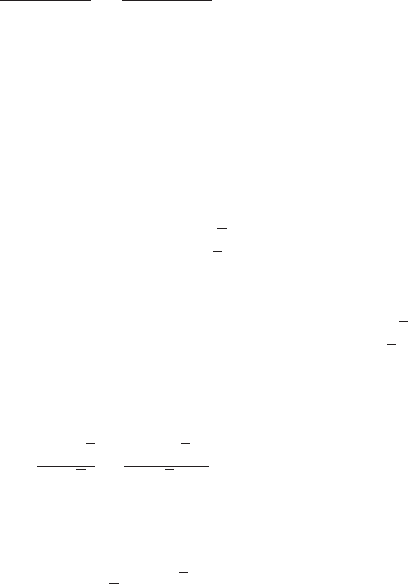
5.3. Геометрический смысл производной 137

Доказательство Воспользуемся двумя фактами. Во-первых, согласно тео-

реме о геометрическом смысле производной функции, заданной параметри-

чески (см. теор. 78, стр. 135), касательный вектор к кривой p(u) в точке,

отвечающей значению параметра u = u

— это вектор, составленный из

производных (p



),p



)).

Во-вторых, касательная к кривой проходит через точку с координатами

),p

)). Поэтому, по теореме о каноническом уравнении прямой (см.

теор. 101, стр. 215), получим:

x − p

)



)

y − p

)



)

Теорема доказана.

Пример 91 Записать уравнение касательной к кривой, описанной параметриче-

ски:

p(u)=



2cosu

5sinu



в точке, отвечающей значению параметра u = π/4. Вычислим значение функции

при u = π/4:

p(π/4) =



2cosπ/4

5sinπ/4





√

2/2



Далее вычислим значение производной при значении параметра u = π/4:



(u)=



−2sinu

5cosu



, поэтому p



(π/4) =



−2sinπ/4

5cosπ/4





−

√

2/2



Теперь мы можем воспользоваться теоремой о касательной к кривой, описанной

параметрически (см. теор. 80, стр. 136):

l :

x −

√

−

√

y − 5

√

2/2

√

2/2

При помощи свойств пропорций из полученного канонического уравнения каса-

тельной можно вывести ее явное уравнение:

l : y = −

x +5

√

2 .

138 Глава 5. Математический анализ

Глава 6

Интерполяция кривых

В качестве приложения математического анализа мы рассмотрим техни-

ку построения различных кривых по некоторым известным заранее их ха-

рактеристикам

. Таким образом, в конце книги мы переходим к вопросам

интерполяции кривых.

Имеются различные подходы к формированию криволинейной траектории,

и, как следствие, различные типы интерполяций (см. опр. 37, стр. 93).

Если требуется, чтобы кривая проходила через набор заранее известных то-

чек, то применяется прием точной интерполяции (см. раздел 6.1, стр. 139).

Этот алгоритм используется во многих графических приложениях при фор-

мировании так называемых трехточечных кривых.

Если при построении кривой существенную роль играют направления, в

которых кривая проходит через узловые точки, то используется интерпо-

ляция в форме Эрмита (см. раздел 6.2, стр. 143). Этот прием лежит в основе

постороения так называемых кривых Безье.

При построении так называемых B-сплайнов, от формируемой кривой тре-

буется, чтобы она проходила вблизи от опорных точек (точнее говоря, каж-

дый ее сегмент должен лежать в пределах выпуклой оболочки последова-

тельных четырех точек ее опорного ансамбля)

В этой главе мы теоретически обоснуем алгоритмы интерполяции и рссмот-

рим ряд примеров. Практические задачи, относящиеся к этой главе пред-

ставлены в приложениях (см. приложение C.3, стр. 218).

6.1 Точная интерполяция

Точная интерполяция (в отличие от кривых Безье или B-сплайнов) редко

используется в графических системах. Однако принципы, которые исполь-

зуются при проведении точной интерполяции, позволяют понять механизм

интерполяционных алгоритмов в общем случае.

Еще раз отметим, что приложения математического анализа весьма обширны и вовсе

не ограничиваются исследованием кривых.

Этот прием мы не будем рассматривать, читатель может ознакомиться с ним в мо-

нографии Эдварда Энджела [E].

139

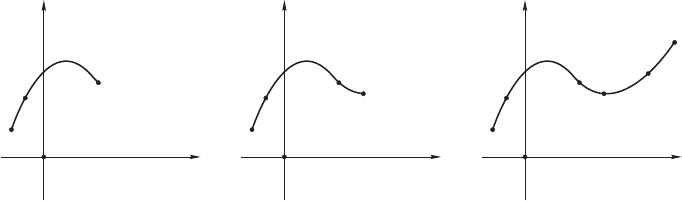
140 Глава 6. Интерполяция кривых

Поэтому мы начинаем изучение интерполяционных алгоритмов с точной

интерполяции.

(a) Трехточечная точная

интерполяция.

(b) Четырехточечная точ-

ная интерполяция.

терполяция.

Рис. 6.1: Кривые, точно интерполирующие опорный ансамбль.

Определение 62 (точная интерполяция) Пусть на плоскости π фик-

сирован некоторый набор точек A

,...,A

, который мы будем называть

опорным ансамблем. Точной интерполирующей кривой для данного ансаб-

ля называется кривая C, проходящая через каждую точку ансамбля ровно

по одному разу и в указанном порядке.

Описание этой кривой в виде полиномиальной параметризации называется

точной интерполяцией данного ансамбля.

Заметим, что задача точной интерполяции имеет смысл для любого набора

точек. Однако следует иметь в виду, что с ростом числа точек, входящих

в ансамль, степень параметризующих его многочленов также растет: для

набора из n точек соответствующие многочлены будут иметь степень n −

1. Производить вычислительные операции с такими многочленами весьма

затруднительно.

Поэтому на практике, как правило, ограничиваются набором из четырех

или даже трех точек, в большинстве случаев характеристики результиру-

ющей кривой оказываются вполне приемлемыми.

Теорема 81 (точная квадратичная интерполяция) Для любого опор-

ного ансамбля, состоящего из трех точек A(x

), B(x

), C(x

)

существует единственная точно интерполирующая его кривая, являющая-

ся квадратичной параметризацией вида:

p(u)=



+ a

u + a

+ a

u + a



причем коэффициенты параметризующих многочленов вычисляются одно-