Непейвода Н.Н. Прикладная логика

Подождите немного. Документ загружается.

5.4. ФУНКЦИИ

101

Поэтому соответствия, для которых ∀x ∈ X ∃1 y ∈ Y (x, y) ∈ R, назы-

вают функциональными. Часто функциональные соответствия отожде-

ствляются с функциями, но такое отождествление не всегда правомер-

но даже в классической математике (в частности, в областях, базирую-

щихся на теории категорий). Другое дело, что любое соответствие фор-

мы

R = {(x, y)|y = f(x)} является функциональным, и в математи-

ке очень стараются, чтобы по любому функциональному соответствию

можно было определить функцию

. Если же мы интересуемся вычи-

слимостью либо определимостью, то на первый план решительно вы-

ходит первая составляющая понятия функции — наличие правила.

Определение 5.4.1.

Функция

представляется в теории множеств как

тройка

hX, Y, Ri,

где

R ⊂ X × Y

— функциональное соответствие.

называется

обла-

стью определения f

— ее

областью значений

. Область определения

обозначается

Dom f

, а область значений —

Val f

Прошу обратить внимание на различие области значений и образа

функции. f hXi ⊂ Y , но равенства обычно нет.

В последнее время композиция функций в математике определяется

в соответствии с композицией отношений:

(f ◦ g)(x) = g(f(x)),

а чтобы при композиции функции не переставлялись,и применение функ-

ций во многих местах (в частности, в работах по алгебре) стали писать

“наоборот”

: xf.

Определение 5.4.2. (Важные классы функций)

Инъекция

(однозначное отображение) — такая функция

, что

∀x ∈ X ∀y ∈ X(f(x) = f(y) ⇔ x = y).

Иногда ради этого даже логику изменяют; в главе, посвященной конструктивным

логикам, мы с этим немного разберемся.

Неразбериха с порядком функций при композиции длилась несколько десятилетий.

“Прямая” школа считала в точности наоборот:

(f ◦ g)(x) = f (g(x)), и до сих пор во

многих работах по математическому анализу и дифференциальным уравнениям при-

держиваются такого определения. В принципе, здесь что в лоб, что по лбу, но не запу-

тывайтесь!

102

ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

Сюръекция

(отображение на) —

∀y ∈ Y ∃x ∈ X f(x) = y.

Биекция

(взаимно-однозначное отображение) — функция, у кото-

рой существует обратная, т. е. функция, графиком которой служит

отношение, обратное к графику

Таким образом, для сюръекций f hDom fi = Val f. Для инъекций

множество f

−1

hyiвсегда не более чем одноэлементно (здесь f

−1

— от-

ношение, обратное к f, оно не обязательно является функцией, и поэто-

му использовано обозначение образа, принятое для соответствий). Еще

две важных характеризации инъекций и сюръекций на языке компози-

ций заслуживают отдельного рассмотрения и доказательства.

Предложение 5.4.1. (Композиции с инъекциями и сюръекциями)

1. Композиция двух инъекций — инъекция.

2. Композиция двух сюръекций — сюръекция.

f : X → Y инъекция тогда и только тогда, когда для любых двух

отображений g

, g

из Z в X

◦ f = g

◦ f ⇔ g

= g

4. f : X → Y сюръекция тогда и только тогда, когда для любых

двух отображений g

, g

из Y в Z

f ◦ g

= f ◦ g

⇔ g

= g

5. f : X → Y инъекция тогда и только тогда, когда существует

функция g : Y → X (называемая накрытием, ассоциированным

с f), такая, что

∀x(x ∈ X ⇒ g(f(x)) = x).

(Другими словами, f ◦ g = id

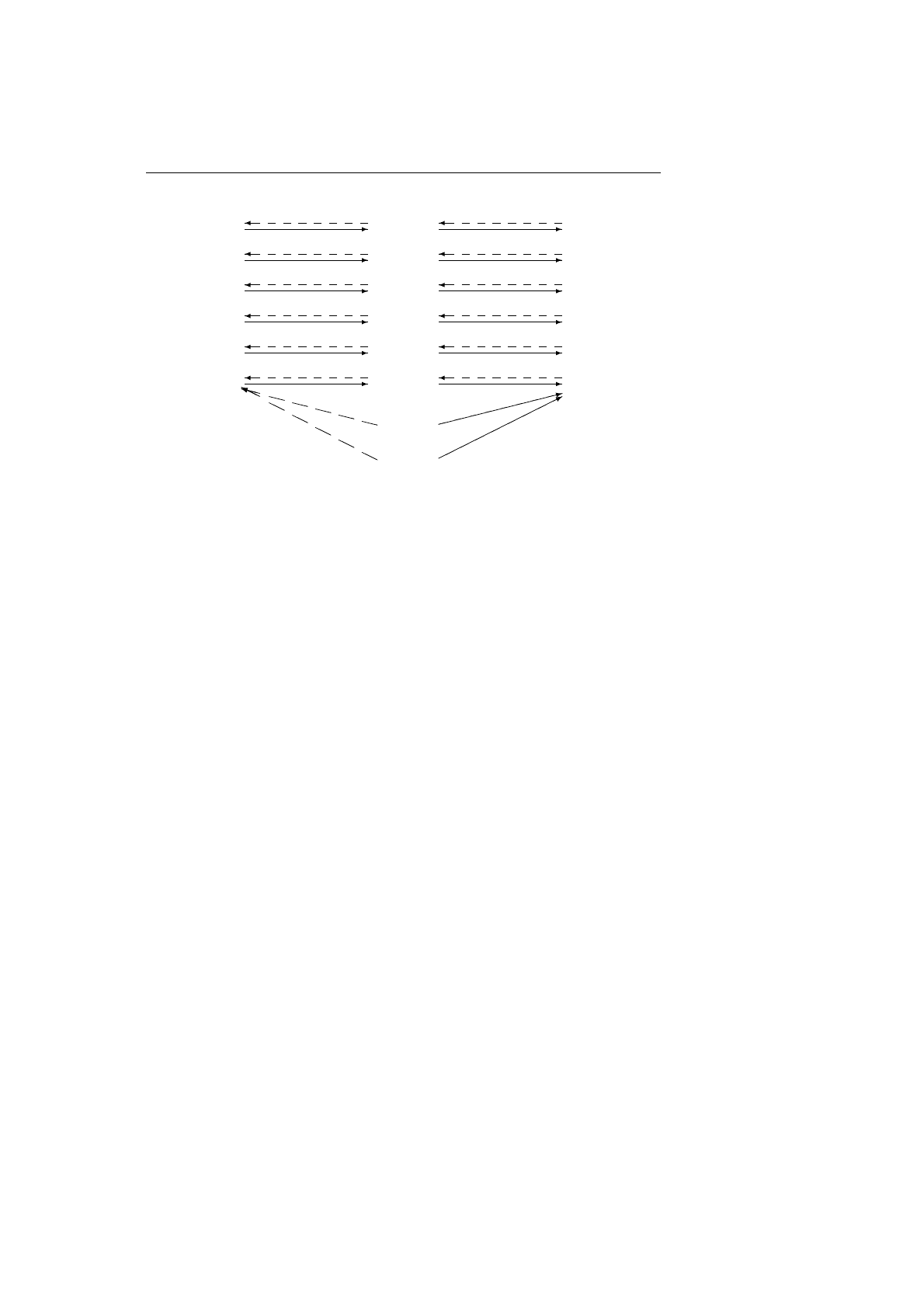
5.4. ФУНКЦИИ

103

X Y

•

• •

•

X Y

•

• •

•

Рис. 5.7: Инъекция и накрытие, сюръекция и ретракция

f : X → Y сюръекция тогда и только тогда, когда существует

функция g : Y → X (называемая ретракцией, ассоциированной с

f), такая, что

∀x(x ∈ Y ⇒ f(g(x)) = x).

(Другими словами, g ◦ f = id

Доказательство. Пункты 1, 2 и 4 остаются в качестве упражнений чи-

тателю.

Доказательство пункта 3. Пусть

f — инъекция из X в Y . Пусть

◦ f = g

◦ f . Тогда для произвольного x f(g

(x)) = f(g

(x)). Но

по инъективности f отсюда следует g

(x) = g

(x). Поскольку вывод

сделан для произвольного x, g

= g

, что и требовалось установить. Те-

перь обратно.Пусть для всех g

, g

, таких, что g

◦f = g

◦f, выполнено

равенство g

= g

. Возьмем произвольные x

, x

. Пусть f(x

) = f(x

Теперь возьмем одноэлементное множество Z = {z

} и построим два

отображения из Z в X, такие, что g

) = x

, g

) = x

. Поскольку

f(g

)) = f(g

)), а других значений аргумента нет, g

◦f = g

◦f.

Значит, в частности, g

) = g

), и x

= x

. Прошу Вас обратить

внимание, что в этом доказательстве нет рассуждений от противного.

Поэтому данное свойство инъекций весьма устойчиво при смене логи-

ки.

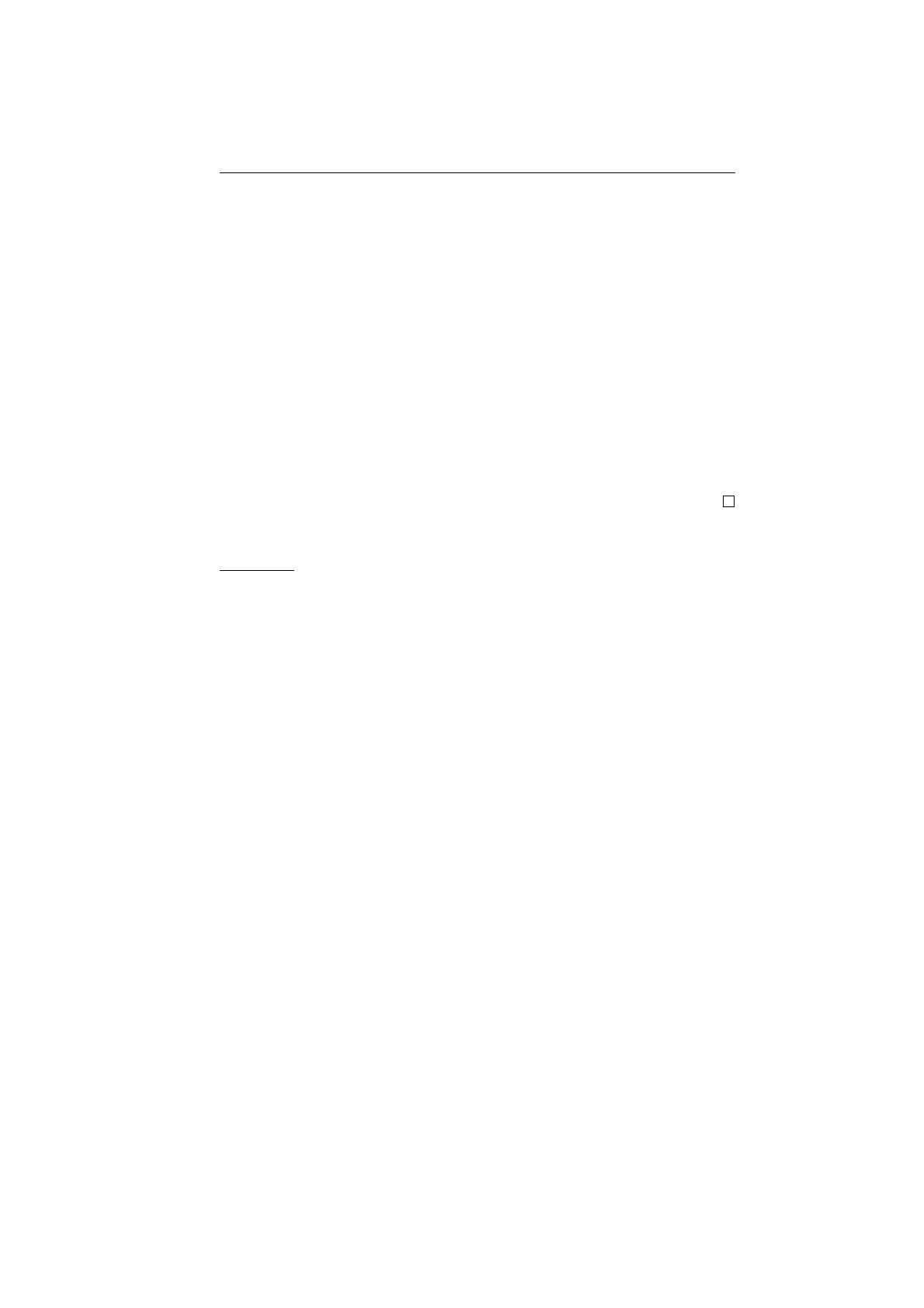
104

ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

Доказательство пункта 5. Пусть у f есть ассоциированное с ним на-

крытие g. Покажем, что тогда f — инъекция. В самом деле, возьмем

произвольные x

, x

, такие, что f (x

) = f (x

). Тогда g(f(x

)) = x

g(f(x

)) = x

. Теперь в обратную сторону. Пусть f — инъекция. По-

строим накрытие

следующим образом: если

y ∈ f hDom f i

, то имеет-

ся единственное

x, такое, что f(x) = y. Оно и будет значением функции

g. Если же y /∈ f hDom fi, то такого x вообще нет, и можно задать зна-

чение g равным произвольно выбранному элементу x

Доказательство пункта 6. Поскольку f — сюръекция, для каждого

y ∈ Val f множество R

−1

hyi непусто. Сопоставим каждому y какой-

либо из элементов R

−1

hyi. Полученная функция и будет искомой ре-

тракцией

Обратная импликация очевидна, поскольку, чтобы вернуться к ар-

гументу, нужно его порою выдавать в качестве значения, что и является

определением сюръекции.

Предложение 5.4.2. Функция является биекцией тогда и только тогда,

Здесь есть тонкость! Прямое и обратное рассуждения принципиально различают-

ся по логическому статусу. Если прямое рассуждение весьма устойчиво, то обратное

содержит внешне безобидный шаг, требующий анализа бесконечно большого объема

информации: проверка, принадлежит ли

y f hDom f i. Поэтому вторая часть данной

эквивалентности легко рушится при замене логики и даже просто при отходе от тео-

рии множеств в качестве основания математики.

А здесь ситуация еще хуже. Подумайте, а как мы выберем по элементу из каждого

−1

hyi? То, что такой выбор можно осуществить, на самом деле эквивалентно одной

из аксиом современной теории множеств, причем аксиоме, чаще всего берущейся под

сомнение: аксиоме выбора. Она гласит, что по любому всюду определенному соответ-

ствию можно построить вложенное в него функциональное. Из нее следуют многие

приятные теоремы традиционной математики и некоторые неприятные, например, те-

орема Куратовского о том, что яблоко можно разрезать на четыре части таким образом,

что из них можно сложить два таких же яблока. В науке всегда так: сильный принцип,

полезный в одних отношениях, вреден и сбивает с толку в других областях. Ни один по-

лезный научный результат не универсален, потому что наука — отрасль человеческого

знания, а человек несовершенен, и поэтому его знания также с необходимостью несо-

вершенны. Так что если кто-то уверяет Вас, что его метод всегда хорош, то это либо

жулик, либо человек, слишком увлекшийся своей идеей, настолько, что она уже нахо-

дится у него на стадии перехода из ценной в сверхценную (‘ценная’ здесь — обычная

неформальная оценка, ‘сверхценная’ — термин из психиатрии, применяемый, когда че-

ловек зацикливается на одной идее и не видит больше ничего вокруг). Надо сказать, что

нынешняя система организации науки, внедрившая в нее рекламу, которая всегда была

противопоказана науке, поощряет такое жульничество, будьте осторожнее и осмотри-

тельнее!

5.4. ФУНКЦИИ

105

когда она является и инъекцией, и сюръекцией.

Доказательство. Пусть отношение

R — график функции f. Рассмо-

трим отношение R

−1

. Поскольку f — сюръекция, для каждого x ∈ Y

существует y ∈ X, (x, y) ∈ R

−1

. Поскольку f — инъекция, из (x, y

) ∈

−1

, (x, y

) ∈ R

−1

следует y

= y

. Таким образом, R

−1

— функцио-

нальное отношение.

Обратная функция, если она существует, обозначается f

−1

Предложение 5.4.3. f ◦ f

−1

= Id

Dom f

, f

−1

◦ f = Id

Val f

Доказательство оставляется в качестве упражнения.

Определение 5.4.3.

Множества

называются

равномощными

,если

имеется биекция

на

(обозначается

X = Y

). Мощность множества

не больше мощности множества

Y (X 6 Y )

, если имеется инъек-

ция из

. Множество

покрывает множество

X (X < Y )

, если

имеется сюръекция

на

Теорема 5.2. (Кантор, Шредер, Бернштейн) Если X 6 Y и Y 6 X,

то X и Y равномощны.

Доказательство. Пусть X 6 Y и Y 6 X. Тогда имеются две инъекции:

f : X → Y , g : Y → X. Если хоть одна из них является сюръекцией, то

эквивалентность установлена. Если ни одна из них не является сюръек-

цией, то множество X \g hY i непусто. Возьмем произвольный элемент

этого множества. Возьмем отношение

= {(x

, x

) | x

∈ X & x

= g(f(x

))}.

Рассмотрим его транзитивное замыкание R

∞

. Образ x

при этом замы-

кании либо конечен, либо бесконечен. Рассмотрим эти два случая.

Пусть образ R

∞

i конечен. Тогда он состоит из конечного мно-

жества элементов

, x

= g(f(x

)), x

= g(f(x

)), . . . , x

= x

n−1

g(f(x

)) = x

для некоторого i < n. Но поскольку f ◦ g — инъекция,

i = 0. В самом деле, если i 6= 0, то i = j +1, но тогда x

j+1

= g(f(x

)) =

g(f(x

)), где x

6= x

, чего не может быть. Но по предположению x

∈

X \ g hY i, и соответственно, нет такого y, что x

= g(y).

106

ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

Значит, остается лишь случай, когда образ x

бесконечен. Все эле-

менты этого образа, очевидно, лежат в g hY i. Докажем теперь, что обра-

зы разных x ∈ X \g hY i при соответствии R

∞

не пересекаются. Рассу-

ждение аналогично тому, с помощью которого мы опровергали конеч-

ность

∞

. Возьмем произвольные

x, y ∈ X \ g hY i

. Если их обра-

зы пересекаются, то некоторые из

равны некоторым из y

. Возьмем

наименьшее такое n. Если оно не 0, то x

n−1

6= y

m−1

, но g(f (x

n−1

)) =

g(f(y

m−1

)).

Теперь построим, пользуясь выше установленным разбиением X,

биекцию Y на X. Для этого видоизменим функцию g. Положим

(y) =



g(y) ¬∃x(g(y) ∈ R

∞

hxi & x ∈ X \ g hY i)

n−1

∃x ∃n(x ∈ X \ g hY i & g(y) ∈ R

∞

hxi & g(y) = x

)

Итак, все последовательности x

сдвигаются на один элемент, и в ре-

зультате g

, оставаясь инъекцией, становится и сюръекцией.

Понятие равномощности дает возможность классифицировать мно-

жества по отобразимости друг на друга

Прежде всего конечные множества равномощны тогда и только то-

гда, когда у них одинаковое количество элементов. Это можно было бы

“доказать,” но уже с конца XIX века известно, что на самом деле лишь

понятие равномощности дает возможность корректно определить ко-

нечное множество в теории множеств.

Определение 5.4.4.

Множество

называется

конечным

, если оно рав-

номощно множеству

{x | x ∈ N & x < n}

для некоторого

n ∈ N

Количество элементов в конечном множестве будем обозначать

В упражнениях разбираются другие попытки определить конечные

множества.

Соответственно, бесконечному множеству чаще всего дают в ма-

тематике негативное определение: бесконечное множество — множе-

ство, не являющееся конечным. Нетривиальное определение бесконеч-

ного множества дал Рассел:

Обычно в книгах по математике пишут, что по числу элементов. Это верно лишь

для конечных множеств. Для бесконечных, скорее, это классификация по сложности

представления. Далее мы познакомимся подробнее с тем, почему общепринятые пред-

ставления не верны и в данном случае.

5.4. ФУНКЦИИ

107

Определение 5.4.5.

Бесконечное множество — такое множество

, что

существует взаимно-однозначное отображение

на какое-либо под-

множество

Y ⊂ X & Y 6= X

Таким образом, бесконечное множество равномощно своему под-

множеству

.Безусловно, математик обязан обосновать, что любое мно-

жество либо конечно, либо бесконечно. Самый простой и одновременно

выявляющий некоторые скрытые трудности путь к этому — через кон-

кретный вид бесконечных множеств: счетные множества.

Определение 5.4.6. Счетное

множество — множество, равномощное

множеству натуральных чисел

Предложение 5.4.4. Если множество содержит счетное подмноже-

ство, то оно бесконечно.

Доказательство. Пусть имеется биекция

f множества натуральных чи-

сел на Y ⊂ X. Тогда построим следующее взаимно однозначное отобра-

жение ϕ X на X \f(0). Если x /∈ Y , то положим ϕ(x) = x. Если x ∈ Y ,

x 6= f(0), то существует такое n ∈ N, что x = f(n + 1). Тогда положим

ϕ(x) = f(n).

Предложение 5.4.5. Всякое бесконечное множество содержит счет-

ное подмножество.

Доказательство. Пусть имеется биекция

f множества X на Y ⊂ X,

Y 6= X. Тогда возьмем какое-либо x

∈ X \ Y . f(x

) 6= x

, обозначим

его x

. Далее, подобно тому, как делалось в теореме Кантора-Шредера-

Бернштейна, положим x

n+1

= f(x

), и так же, как в упомянутой теоре-

ме, можно показать, что все x

различны. Множество

| i ∈ N}

и есть искомое счетное подмножество X.

Видимо,первым обратил на это внимание кардинал Николай Кузанский , выдающий-

ся схоласт XV века. Он применил это для обоснования того, что триединство Бога не

является логическим противоречием, поскольку Бог — бесконечная сущность (одно из

очень немногих корректных применений математики в богословии). Галилей, видимо,

независимо, заметил, что множество натуральных чисел взаимно-однозначно отобра-

жается, в частности, на множество четных чисел, и опубликовал это в математическом

тексте. Отсюда Галилей сделал вывод, что нельзя говорить о множестве всех натураль-

ных чисел, поскольку иначе нарушается фундаментальная аксиома Евклида: «Целое

больше части». В дальнейшем математики просто отказались от этой аксиомы, заме-

тив, что ее нельзя выразить на математическом языке.

108

ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

Предложение 5.4.6. Если множество не является конечным, то оно

содержит счетное подмножество.

Доказательство. Рассмотрим следующее отношение между конечны-

ми подмножествами

= {(Y, Z) | Y ⊂ X & Z ⊂ X & Y ⊂ Z &

Y + 1 =

Z}.

Итак, данное отношение связывает между собою конечные множества,

второе из которых содержит один дополнительный элемент вдобавок к

элементам первого. Очевидно, что E не определено на Y тогда и только

тогда, когда Y = X. Но поскольку по условию X не является конечным,

E всегда определено.

Поэтому начнем с некоторого одноэлементного множества V

⊂ X,

и для каждого

выберем

i+1

как произвольный элемент

E hV

. Оче-

видно, что

⊂ V

при i < j, и объединение возрастающей последова-

тельности

∞

[

i=0

и есть искомое счетное подмножество X.

Итак, мы показали, что, действительно, каждое множество либо ко-

нечно, либо бесконечно и что счетные множества являются в некотором

смысле минимальными среди бесконечных. Но счетных множеств не

так уж мало.

Пример 5.4.1.

Множество рациональных чисел счетно. В самом деле,

любое рациональное число представимо несократимой дробью

n/m

где

m > 0

. Дробей с суммой числителя и знаменателя

— конечное

число, поэтому их можно расположить в порядке возрастания

, за ни-

ми все дроби с суммой числителя и знаменателя

n + 1

и так далее.

На самом деле мы дали общий способ, как показать счетность лю-

бого множества, элементы которого представимы конечной последова-

тельностью из конечного числа символов.

Здесь опять применяется аксиома выбора; но на самом деле здесь используется бо-

лее слабая ее форма, вызывающая меньше сомнений и, самое главное, совместимая с

аксиомой детерминированности, также естественной, но противоречащей аксиоме вы-

бора. Тех, кто интересуется данным вопросом, можно отослать, например, к книге [17].

См. также § 10.5.1.

5.4. ФУНКЦИИ

109

Мощность множества натуральных чисел обычно обозначается ℵ

(ℵ — первая буква еврейского алфавита, произносящаяся ‘алеф’). Про-

стейший пример бесконечного множества, не являющегося счетным,

Теорема 5.3. Множество действительных чисел несчетно.

Доказательство. Пусть имеется некоторое отображение

множества

N в действительные числа из отрезка [0, 1] (последовательность). По-

строим по ней представленное в троичной системе число b, не входя-

щее в данную последовательность и, более того, такое, что от данного

оно отличается уже первыми n + 1 членами троичного разложения.

не принадлежит по крайней мере одному из трех отрезков [0, 1/3],

[1/3, 2/3], [2/3, 1]. Выберем первую после запятой троичную цифру так,

чтобы b не попало в тот же отрезок, что и a

. Далее, пусть, например,

первая цифра это 1. Тогда a

не принадлежит по крайней мере одному

из трех отрезков (а возможно, и ни одному из них, если оно не попада-

ет в [1/3, 2/3]) [1/3, 4/9], [4/9, 5/9], [5/9, 2/3]. Выберем вторую троич-

ную цифру таким образом, чтобы a

разошлось с b. Так же продолжаем

и далее. Итак, никакая последовательность не может перечислить всех

действительных чисел.

Обратим Ваше внимание на одну тонкость в приведенном доказа-

тельстве. Может показаться, что мы брали троичное, а не двоичное раз-

ложение с той целью, чтобы избавиться от хлопот с числом

1/2. Ко-

нечно, часто математики поступают именно так, делая гораздо труднее

реализуемый алгоритм лишь потому, чтобы не рассматривать отдель-

но несколько исключительных случаев. Но здесь причина другая. Мы

постарались, чтобы данное доказательство было абсолютным, сохра-

няющим силу не только в традиционной математике, но и в ее извест-

ных модификациях. Мы, в частности, нигде не предполагали, что дей-

ствительные числа точно известны, и проследили, чтобы для каждого

использованного в рассуждении отношения между ними можно было

указать, с какой точностью его достаточно проверить.

Про множества,равномощные множеству действительных чисел,го-

ворят, что они имеют мощность континуума, эта мощность обозначает-

ся

Пример 5.4.2.

Любое конечномерное пространство

имеет мощность

континуума.

110

ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

В самом деле, воспользуемся определением действительных чисел

через двоичные разложения и построим инъекцию из

следую-

щим образом (

(x)

в данной формуле —

-тый знак числа

(ϕ((x

, . . . , x

)))

n∗i+k

= (x

k+1

)

(5.15)

Итак, двоичные знаки получившегося числа соединяют двоичные знаки

всех аргументов, и, очевидно, каждое из

однозначно восстанавлива-

ется по значению

ϕ((x

, . . . , x

))

. Инъекция

очевидна.

По теореме Кантора-Шредера-Бернштейна,

равномощны.

Вопрос, существуют ли множества мощности, промежуточной меж-

ду счетной и континуумом, не разрешим в принятой аксиоматике тео-

рии множеств. Предположение, что таких множеств нет, носит название

континуум-гипотезы.

Теорема 5.4. (Теорема Кантора) Множество всех подмножеств мно-

жества

X, обозначаемое

, имеет мощность б

ольшую, чем X.

Доказательство. Очевидно, что имеется инъекция

X в

. Докажем,

что обратной инъекции нет.

Приведем предположение, что f — такая инъекция, к абсурду. Для

этого построим множество

= {x | x ∈ X & x /∈ f

−1

hxi.

Тогда f(K) ∈ K ⇔

f(K) ∈ K.

Из теоремы Кантора следует парадокс Кантора, показывающий, что

множества всех множеств не существует.

(Парадокс Кантора) Множество всех множеств

U содер-

жит любое другое множество как подмножество, и значит,

если V — некоторое множество, то имеется инъекция V в

U. Но тогда имеется и инъекция

в U, что противоречит

теореме Кантора.

Таким образом, не всякое выразимое на языке логики свойство мно-

жеств определяет множество (на самом деле проще всего здесь при-

мер из парадокса Рассела: несуществование

{x | x /∈ x}). В современ-

ной математике принято совокупности множеств и других математиче-

ских объектов, удовлетворяющих данному свойству, называть класса-