Непейвода Н.Н. Прикладная логика

Подождите немного. Документ загружается.

Глава 6. Индукция

и определения

§ 6.1. О РАЗНЫХ ВИДАХ ИНДУКЦИИ

Все вы знакомы с методом математической индукции, применяемым

к утверждениям, содержащим свободную переменную по натуральным

числам. Приведем пример доказательства по индукции.

Пример 6.1.1.

Докажем, что сумма трех последовательных кубов нату-

ральных чисел делится на 9.

Базис. 1

+ 2

+ 3

= 36

и делится на 9.

Шаг.

Чтобы произвести шаг, нужно

предположить

доказываемое

утверждение для

и затем

доказать

его для

n + 1

. Пусть

+ (n +

+ (n + 2)

делится на 9. Тогда

(n + 1)

+ (n + 2)

+ (n + 3)

(n + 1)

+ (n + 2)

+ n

+ 9n

+ 27n + 27 =

+ (n + 1)

+ (n + 2)

) + (9n

+ 27n + 27).

Но все слагаемые в последней скобке делятся на 9, а первая скобка де-

лится на 9 по предположению, значит, и исходная сумма делится на 9.

Таким образом, мы установили, что делимость суммы, начинающейся с

, влечет делимость суммы, начинающейся с

n + 1

Следовательно, утверждение доказано для всех

Итак, в математической индукции имеются базис — утверждение,

что свойство выполнено для самого маленького из рассматриваемых чи-

сел, и шаг — обоснование перехода от числа n к числу n + 1. На язы-

ке логики метод математической индукции представляется следующей

формулой:

A(0) & ∀n (A(n) ⇒ A(n + 1)) ⇒ ∀n A(n). (6.1)

142

ГЛАВА 6. ИНДУКЦИЯ И ОПРЕДЕЛЕНИЯ

Пример 6.1.2.

Докажем, что

плоскостей, проходящих через одну точ-

ку, никакие три из которых не проходят через одну прямую, делят про-

странство на

= n(n − 1) + 2

частей.

Базис. A

= 2

Шаг.

Пусть утверждение доказано для

. Докажем его для

n + 1

Пусть

n+1

—

n + 1

-я плоскость. Каждая область разбиения пред-

ставляет собой многогранный угол, вершиной которого является общая

точка всех плоскостей

. Число частей при разбиении

n + 1

-ой плоско-

стью равно (здесь мы применяем предположение индукции)

число многогранных углов, разбиваемых на две части

n+1

Поскольку сечение каждого из таких двугранных углов плоскостью

n+1

является плоским углом с вершиной в

,число разбиваемых двугранных

углов не может быть больше

, а поскольку никакие три плоскости не

пересекаются по прямой, их не может быть меньше

. Таким образом,

n+1

= A

+ 2n = (n + 1)n + 2.

Пример 6.1.3.

Пусть на плоскости имеется точечный прожектор, осве-

щающий сектор внутри угла

α < 180

◦

. Пусть заданы

непересекаю-

щихся отрезков (которые могут смыкаться концами). Докажем, что то-

гда выполнено одно и только одно из трех:

1. Прожектор не освещает ни одной точки ни одного отрезка.

2. Прожектор освещает конец хотя бы одного из отрезков

3. Имеется отрезок

(часть которого, пересекающаяся с сектором,

полностью освещена), полностью затеняющий все остальные, пе-

ресекающиеся с сектором освещения.

Как всегда при решении задачи, заданной в физических терминах, мате-

матик должен прежде всего подумать о том, как перевести все понятия

на математический язык. Итак, у нас есть точка

, в которой располо-

жен прожектор. Первое предположение, неявно спрятанное в физиче-

ской задаче, следующее: ни один из отрезков не проходит через точку

. Далее, что означает, что точка

освещена либо затенена?

Точка

освещена, если отрезок

находится внутри осве-

щенного сектора и не пересекается ни с одним из отрезков

, кроме, возможно, самой точки

6.1. ОБ ИНДУКЦИЯХ

143

Точка

затенена отрезком

,если внутри отрезка

встре-

чается точка из

Базис индукции.

Если у нас всего один отрезок

, то он либо пе-

ресекается, либо не пересекается с освещенным сектором. Если он не

пересекается, то выполнена первая возможность. Если же он пересека-

ется, то либо хотя бы один из его концов лежит в освещенном секторе,

либо же оба они лежат вне его. В первом случае соответствующий ко-

нец

освещен (либо же, если отрезок тянется вдоль луча

лежит

на этом луче до

, то освещен

). Во втором возьмем на отрезке про-

извольную точку

, лежащую внутри освещенного сектора. Отрезок не

может лежать вдоль

, так как его концы не освещены, значит, точка

освещена.

Шаг индукции.

Пусть для любой системы из

отрезков имеет место

один из рассмотренных случаев. Рассмотрим систему из

n + 1

отрезка.

Удалим из нее последний отрезок. Рассмотрим три возможных случая

для получившейся системы.

Если ни один из отрезков

, . . . , a

не освещен, то ни один из них

не пересекается с сектором освещения, и все рассматривается точно так

же, как в базисе индукции, в соответствии с положением последнего

отрезка.

Если некоторые из концов отрезков были освещены, то рассмотрим,

затеняет ли их отрезок

n+1

. Если все освещенные концы им затеняют-

ся, то остается рассмотреть два подслучая:

1. Хотя бы один из концов

n+1

лежит в секторе освещения. Тогда

хотя бы один из его концов будет освещен, и выполнен второй слу-

чай.

2. Оба конца этого отрезка лежат вне сектора освещения. Тогда он

затеняет все остальные отрезки, а его пересекающаяся с сектором

освещения часть полностью освещена.

В программировании математическая индукция соответствует ци-

клам типа пересчета (

for

i:=0

языка Паскаль).

Применение математической индукции, конечно же, содержит мно-

го тонкостей. Приведем несколько софизмов, доказываемых при помо-

щи неправильного применения индукции.

Пример 6.1.4.

Докажем, что все лошади одного цвета.Действуем по ин-

дукции. Параметр индукции — число

лошадей в их множестве.

144

ГЛАВА 6. ИНДУКЦИЯ И ОПРЕДЕЛЕНИЯ

Базис.

n = 1

. Одна лошадь, естественно, одного цвета. Точнее, все ло-

шади, принадлежащие одноэлементному множеству лошадей, одного

цвета.

Шаг

. Пусть доказано для

. Докажем для

n + 1

. Возьмем произвольное

множество

из

n + 1

лошади. Удалим из него некоторую лошадь

По предположению индукции,

\ {

}

состоит из лошадей од-

ного цвета. Теперь удалим из

некоторую лошадь

и добавим туда

. Полученное множество

также состоит из лошадей одного цвета,

значит,

того же цвета, что и остальные лошади из

, а они являются

элементами

и того же цвета, что и

. Что и требовалось доказать.

Пример 6.1.5.

Докажем, что все ученые — лысые.

Документально засвидетельствовано, что у некоторых академиков

на голове не осталось ни одного волоса. Тогда они, естественно, лысые.

Но если лысому человеку добавить один волос, то он останется лы-

сым. Значит, по индукции получаем, что ученые с любым количеством

волос на голове лысые.

Ошибки найдите сами.

Принцип математической индукции допускает несколько перефор-

мулировок, которые в традиционной математике эквивалентны исход-

ному принципу.

Первая из них — возвратная индукция. Здесь переход происходит

не от одного значения к следующему, а от всех предыдущих значений

к последующему, шаг индукции переводит не от

A(n) к A(n + 1), а от

∀x < n A(x) к A(n). Как ни парадоксально, при таком переходе не тре-

буется базиса индукции. В самом деле, поскольку условие x < 0 тожде-

ственно ложно, то, поскольку из лжи следует все что угодно, имеем

∀x(x < 0 ⇒ A(x)),

а отсюда по шагу индукции имеем A(0).

Соответственно,формулировка принципа возвратной индукции сле-

дующая:

∀x (∀y(y < x ⇒ A(y)) ⇒ A(x)) ⇒ ∀x A(x).

Докажем при помощи возвратной индукции следующее предложе-

ние.

Пример 6.1.6.

Сумма внутренних углов любого плоского

-угольника

без самопересечений равна

π ∙ (n −2)

6.1. ОБ ИНДУКЦИЯХ

145

∙

∙ ∙

A C

Рис. 6.1: Предложение о внутренних углах многоугольника

Для треугольника это доказывается в элементарной математике, а

многоугольников с числом углов меньше 3 нет. Таким образом, утвер-

ждение индукции доказано для всех

n 6 3

Пусть имеется многоугольник с числом сторон

n > 3

, и для всех

k < n

утверждение индукции уже доказано. Возьмем в многоугольнике

любые три смежные вершины

. Из вершины

либо виден один

из других углов

, либо не виден ни один, и тогда все лучи, лежащие

в угле

ABC

, первой пересекают одну и ту же сторону многоугольника.

В последнем из случаев могу быть еще два подслучая, симметрич-

ных друг другу. Либо на продолжении одной из сторон

первой

встречается некоторая вершина

, либо никакой вершины не встреча-

ется. Тогда могут быть два случая (см. рис. 6.1).

1. Луч первой пересекает одну из сторон многоугольника.Тогда мно-

гоугольник разбивается лучом на два многоугольника. В каждом

из них появляется одна новая вершина

,но пары вершин

{A, E

}

{B, E

}

лежат в разных многоугольниках, так что каждый из них

содержит меньшее число вершин, чем исходный. Пусть один из

них содержит

вершин, а второй —

. Тогда

+ m

= n + 2

(поскольку вершина

теперь принадлежит обоим многоугольни-

кам, а

вообще новая и также принадлежит им обоим). Соответ-

ственно, вычисляя по индукции сумму внутренних углов нашего

многоугольника, получаем:

π ∙ (m

− 2) + π ∙ (m

− 2) = π ∙ (n + 2 − 4) = π ∙ (n − 2).

Хотя мы только что обращали внимание на то, что формально возвратная индукция

базиса не требует, фактически подобие базиса появляется практически в каждом таком

доказательстве, поскольку случаи для наименьших возможных

n обычно приходится

рассматривать отдельно.

Виден — означает, что отрезок BD целиком лежит внутри открытого многоуголь-

ника

146

ГЛАВА 6. ИНДУКЦИЯ И ОПРЕДЕЛЕНИЯ

2. Луч прежде всего входит в вершину многоугольника. Опять-таки

многоугольник разбивается на два многоугольника. В каждом из

них присутствуют две вершины исходного многоугольника

, а все остальные вершины распределены между ними. Каждый

из получившихся многоугольников содержит меньше вершин, чем

исходные, поскольку в нем не присутствует хотя бы одна из вер-

шин

Еще одна переформулировка метода математической индукции бы-

ла известна еще древним грекам, хотя явно сформулировали ее лишь в

XVII веке. Это — метод бесконечного спуска.

Если для каждого натурального числа, удовлетворяющего

свойству

A(n), найдется меньшее, удовлетворяющее этому

же свойству, то чисел n, для которых выполнено A(n), во-

обще нет. Или формально:

∀n (A(n) ⇒ ∃m(m < n & A(m))) ⇒ ∀n ¬A(n). (6.2)

Метод бесконечного спуска получается просто контрапозицией шага из

возвратной индукции по

¬A(n), а попробуйте Вы усмотреть это из их

содержательных формулировок!

Рассмотрим пример применения метода бесконечного спуска.

Пример 6.1.7.

Докажем, что абсурдно предположение, что у каждого

человека мать являлась человеком. В самом деле, за все время суще-

ствования Земли на ней жило конечное число людей. Пусть у каждого

человека мать — человек. Упорядочим людей по моментам рождения.

Список всех бывших людей в порядке времени рождения назовем Кни-

гой Судеб

. Мать рождается раньше своих детей, и поэтому в Книге Су-

деб она стоит раньше. Таким образом, для каждого человека найдется

стоящий раньше него в Книге Судеб.По принципу бесконечного спуска,

получаем, что людей вообще нет и не было, что абсурдно

. Полученное

противоречие доказывает утверждение.

Еще одно следствие из возвратной индукции, эквивалентное ей

принцип наименьшего числа.

Книга Судеб — легендарная книга, в которую Аллах записал еще до сотворения

Земли судьбу каждого человека.

Правда, Диоген искал хотя бы одного человека в Афинах днем с огнем...

Но только в классической математике!

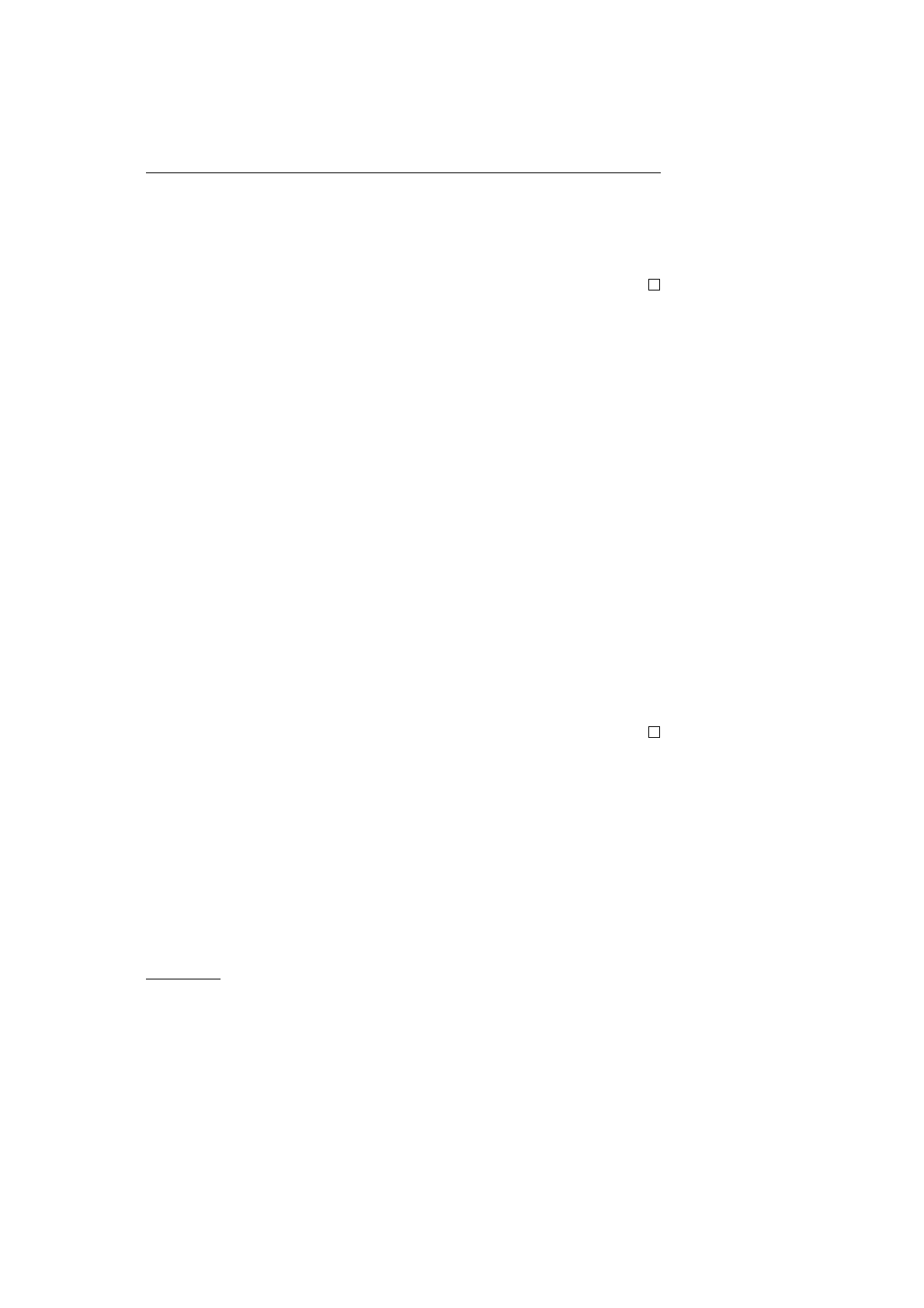
6.1. ОБ ИНДУКЦИЯХ

147

Предложение 6.1.1. Во всяком непустом множестве натуральных чи-

сел найдется наименьший элемент.

Доказательство. Принцип наименьшего числа является контрапозици-

ей принципа бесконечного спуска

Если у нас выполнен принцип наименьшего числа, то, поскольку это

наименьшее число одно и только одно в каждом непустом множестве,

появляется новая кванторная операция: квантор минимизации

μx x ∈

X либо, поскольку подмножество определяется свойством,μx A(x). Та-

кое выражение означает наименьшее число, обладающее данным свой-

ством.

И наконец, рассмотрим еще одну переформулировку возвратной ин-

дукции, также эквивалентную ей

:принцип убывающей последователь-

ности.

Предложение 6.1.2. Всякая убывающая последовательность натураль-

ных чисел конечна.

Доказательство. Если бы она была бесконечна, это противоречило бы

принципу бесконечного спуска. Теперь выведем принцип бесконечного

спуска из конечности убывающих последовательностей. Если бы для

каждого

, удовлетворяющего свойству A(n

), нашлось бы меньшее

его n

i+1

, удовлетворяющее этому же свойству, то получившаяся после-

довательность была бы бесконечной убывающей, чего не может быть.

Таким образом, от противного обоснован метод бесконечного спуска.

Упражнения к § 6.1

6.1.1. Вернемся к ситуации из примера 6.1.3 и несколько видоизменим

ее.

1. Что изменится, если

180

◦

6 α < 360

◦

2. Что изменится, если разрешить счетное число отрезков?

6.1.2. Рассмотрим следующее индуктивное рассуждение.

И не только в классической математике!

148

ГЛАВА 6. ИНДУКЦИЯ И ОПРЕДЕЛЕНИЯ

Пусть даны

джентльменов (натуральных, хорошо воспитанных,

а не одесских) и

бутербродов. Докажем, что все джентльмены

скорее останутся голодными, чем притронутся к бутербродам.

Базис индукции

. Пусть бутерброд всегда один. Тогда приведенное

утверждение очевидно,поскольку следует из благовоспитанности

джентльменов, которые прежде всего думают о том, как не причи-

нить неудобств другому джентльмену, что произошло бы, если бы

джентльмен съел бутерброд и тем самым лишил других такой воз-

можности.

Шаг индукции

. Пусть предложение доказано для

бутербродов.

Добавим еще один. Тогда, если какой-то джентльмен съест бутер-

брод, то он сведет ситуацию к предыдущей, в которой, как уже

было доказано, ни один джентльмен не притронется к бутербро-

ду. Так что настоящий джентльмен на такой шаг не пойдет.

В чем здесь софизм?

§ 6.2. ОБ ИНДУКТИВНЫХ ОПРЕДЕЛЕНИЯХ

Индуктивное определение имеет следующую общую форму:

(Базис индукции) Выражения вида A есть B.

(Шаг индукции) Если мы имеем выражения A

, . . . , A

типа B, то

C, построенное из них, также есть выражение типа B.

С каждым индуктивным определением связан принцип индукции по

построению объекта типа B.

(Базис индукции) Каждый объект вида A обладает свойством θ.

(Шаг индукции) Если A

, . . . , A

обладают свойством θ, то и C им

обладает.

(Заключение индукции) Тогда любой объект типа B обладает свой-

ством θ.

Этот принцип является логическим выражением следующего неяв-

ного пункта, присутствующего в любом индуктивном определении: ни-

каких других объектов типа B, кроме полученных применением правил

его определения, нет. Иными словами, множество объектов типа B —

минимальное из тех, которые включают базисные объекты и замкнуты

относительно шага индукции. В простых определениях эту минималь-

ность можно выразить следующим образом: объект должен получаться

из базисных конечным числом применений шагов определения. Но в

6.2. ОБ ИНДУКТИВНЫХ ОПРЕДЕЛЕНИЯХ

149

современной теории часто приходится рассматривать определения, ко-

торые включают шаги, опирающиеся на бесконечное множество ранее

построенных объектов. Тут индукция остается единственным коррект-

ным и инвариантным способом выражения минимальности

Стоит отметить, что логическая индукция по построению вовсе не

требует однозначности представления объекта в форме, соответствую-

щей одному из пунктов его определения. Но для задания функций ин-

дукцией по построению такая однозначность необходима.

Теперь рассмотрим другие возможности, связанные с индуктивны-

ми определениями. Часто несколько понятий вводятся совместным ин-

дуктивным определением, в котором в каждом шаге могут участвовать

уже построенные понятия разных типов. Для того чтобы превратить

раздельные определения формулы и терма в совместное, достаточно вве-

сти пункт типа: если

A(x) — формула, то εx A(x) — терм

. В совмест-

ных определениях индукцию и рекурсию по построению приходится ве-

сти одновременно для всех понятий. Далее, в математических теориях

широко применяются определения, в шагах которых могут быть ссыл-

ки на бесконечное множество ранее построенных понятий. Они также

допустимы, но, конечно, уже не могут быть прямо перенесены на пред-

ставление данных в программах.

Часто отмечается возможность представления логических формул в

виде дерева. На самом деле в такой же структуре представляются любые

индуктивно определенные понятия. Но называть структуру данных, со-

ответствующую индуктивным определениям, просто деревом несколь-

ко неточно.

Как известно, дерево — это ориентированный граф, в котором име-

ется корень и в любую другую вершину ведет ровно один путь из кор-

ня. Таким образом, по определению графа, ребра, выходящие из любой

вершины дерева, равноправны. Структура же, соответствующая индук-

тивному понятию, является нагруженным деревом, вершинам которого

сопоставлены слова, а ребра помечены согласно роли их назначения в

В теории множеств часто определяют множество объектов типа B при помощи сле-

дующей процедуры: возьмем пересечение всех множеств объектов, включающих базис

определения и замкнутых относительно его шага. Но такое определение, с одной сторо-

ны, включает в себя скрытый порочный круг (

B определяется в том числе и через само

B); с другой стороны, оно не сохраняется при переходе к неклассической логике.

Эти термы были введены Д.Гильбертом. Их семантика — выбрать такое x, что A(x),

если такое

x существует; в противном случае взять некоторое стандартное значение.

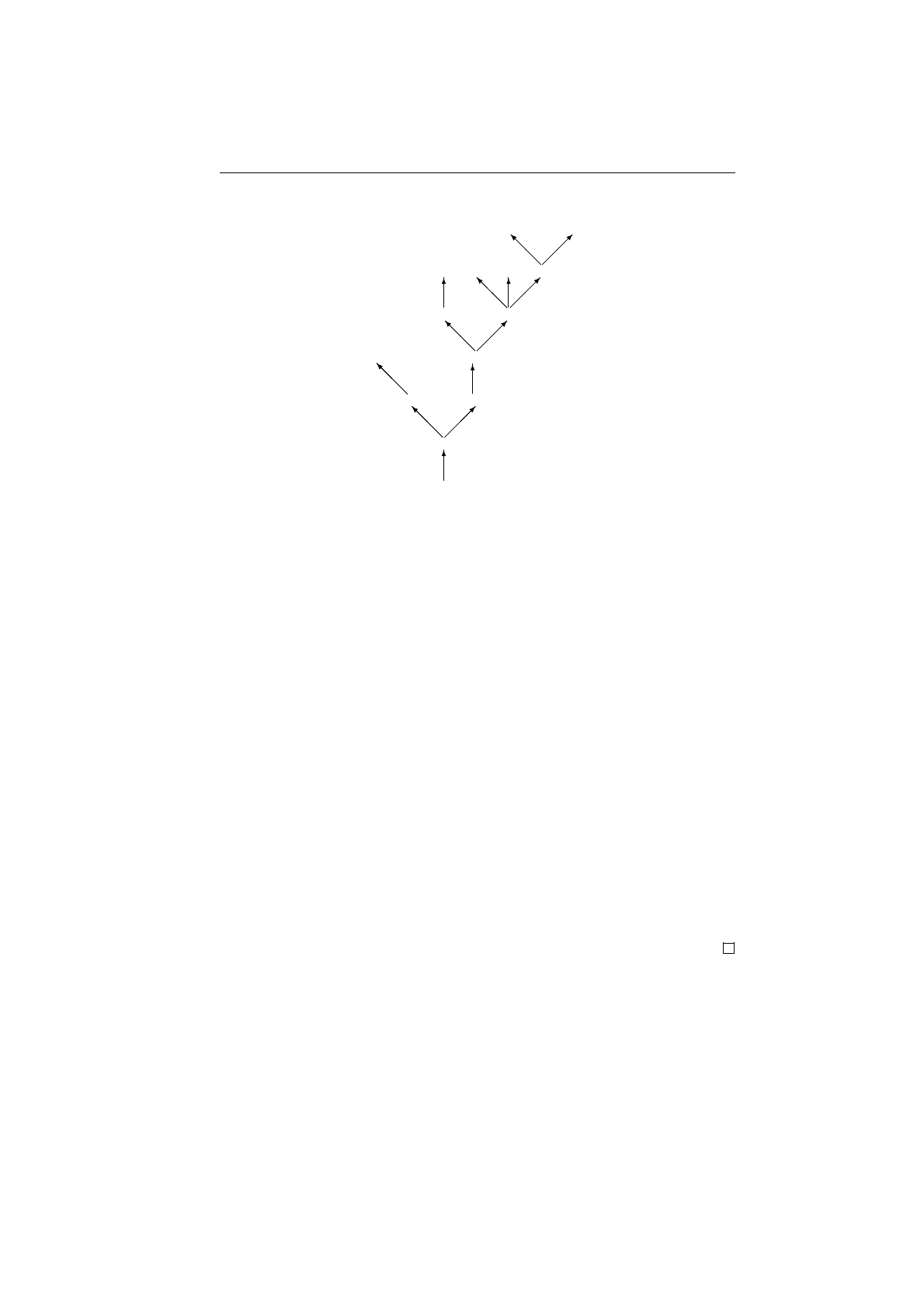
150

ГЛАВА 6. ИНДУКЦИЯ И ОПРЕДЕЛЕНИЯ

∀x (A(x) ⇒ ∃y (B(y) & D (x, y, ϕ(x, y))))

∀x

⇒

∃y

x y ϕ

x y

Рис. 6.2: Формула и соответствующее ей дерево

структуре понятия. Например, на рис. 6.2 даны формула и соответству-

ющее нагруженное дерево.

Рассмотрение деревьев, соответствующих построениям индуктив-

ных объектов, позволяет вывести мощную и не очень зависящую от из-

менений взгляда на математику характеризацию минимальности класса

объектов, задаваемых индуктивным определением. Дерево с конечными

путями — такое, в котором нет ни одного бесконечного пути, и значит,

каждый путь, который не может быть продолжен,заканчивается в листе.

Теорема 6.1. Каждому примеру индуктивно определенного понятия со-

поставляется нагруженное дерево с конечными путями.

Доказательство. Рассуждаем индукцией по построению. Понятиям,

построенным согласно базисам определения, сопоставляются деревья

из одной вершины. Если всем

, участвующим в определении B, со-

поставлены деревья T

, то B сопоставляется дерево, корнем которого

является построение самого B, ветви, выходящие из корня, помечены

номерами i, и за i-той дугой следует дерево T

. Любой путь, выходящий

из B, проходит через какую-то i-тую ветвь и продолжается как путь в T

который конечен по предположению индукции.

Итак, индукцией по определению мы установили соответствие по-

нятий и деревьев с конечными путями. И обратно, деревья с конечны-