Непейвода Н.Н. Прикладная логика

Подождите немного. Документ загружается.

11.2. ПРАВИЛА ЕСТЕСТВЕННОГО ВЫВОДА

301

Рассуждения, в которых применяется правило снятия двойного от-

рицания, называются непрямыми рассуждениями или доказательства-

ми от противного. Порою их путают с приведением к абсурду, но ло-

гический статус этих рассуждений совершенно разный: приведение к

абсурду является определением отрицания, а рассуждение от против-

ного — уже использование нетривиальных его свойств. Докажем теперь

важное выводимое правило: из противоречия следует все что угодно.

Пусть доказаны

A и ¬A. Выведем из них произвольное B.

∗ ¬B



¬A

¬¬B

(11.1)

Итак, доказываем B от противного. Предполагаем его отрицание и, вос-

пользовавшись уже имеющимся противоречием, приходим к ¬¬B, а от-

туда к B. Данный трюк нужен прежде всего затем, чтобы установить,

что правило “из лжи следует все что угодно” (

ex falso quodlibet

средне-

вековых логиков) не нуждается в том, чтобы быть постулированным в

нашей системе. Но пользоваться, конечно, теперь мы им будем.

Поскольку из любого противоречия следует все что угодно, все про-

тиворечия для нас равноправны, и в качестве обозначения произвольно-

го противоречия возьмем логическую константу ⊥ (ложь).

Докажем теперь важную теорему,а именно:закон исключенного тре-

тьего. Тут даже не ясно сначала, с какой стороны подступиться, посколь-

ку дизъюнкцию вроде бы надо выводить при помощи разбора случаев,

а разбирать нечего. Но рассуждая от противного, удается запутаться в

противоречиях, из которых нет другого выхода, кроме того, что при-

знать, что закон исключенного третьего не может быть ложным.

∗ ¬(A ∨ ¬A)



∗ A

|A ∨ ¬A ?!

¬A

A ∨ ¬A ?!

¬¬(A ∨ ¬A)

A ∨ ¬A

(11.2)

Получающиеся противоречия помечены знаком ?! То, что столь простая

формула имеет столь неестественное доказательство, на самом деле до-

302

ГЛАВА 11. ЕСТЕСТВЕННЫЙ ВЫВОД

статочно глубокий факт. Естественный вывод гораздо более тонкий ин-

струмент, чем семантические таблицы, обладающий большой аналити-

ческой силой и легко модифицируемый. Здесь мы получаем первый сиг-

нал о том, что не все тавтологии классической логики равноправны, что

некоторые из них могут иметь более высокий статус, чем другие.

11.2.4. Некоторые полезные выводимые правила

Рассмотрим еще несколько широко применимых выводимых правил.

Во-первых, опираясь на наше доказательство логического закона A ∨

¬A, можно в любой момент разбирать случаи A и ¬A. Далее, пользу-

ясь тем, что из лжи следует все что угодно, можно обосновать правило,

известное нам как сокращающее в семантических таблицах:

A ∨ B ¬A

Как известно, этим правилом часто пользовался Шерлок Холмс, отбра-

сывая все возможные случаи, пока не оставался правильный. А из при-

ведения к нелепости следует правило

modus tollens

традиционной логи-

ки:

A ⇒ B ¬B

¬A

После того, как на практическом занятии разобраны их выводы, вы-

водимыми правилами можно свободно пользоваться при решении задач.

11.2.5. Кванторы

Перейдем теперь к кванторам. Как доказывается утверждение вида

∀x(A(x) ⇒ B(x))?

Берется «произвольное x,такое,что A(x)»и для него доказывается B(x).

В заключительной части этого приема легко узнать правило дедукции

для доказательства импликации A(x) ⇒ B(x). Но вот что такое «про-

извольное x»? Ведь произвольного объекта вообще не бывает, любой

взятый объект конкретен.

На самом деле и здесь мы сталкиваемся с одной из важнейших сто-

рон математической абстракции. Она может включать в себя доброволь-

ный отказ от того, чтобы пользоваться некоторой информацией. В част-

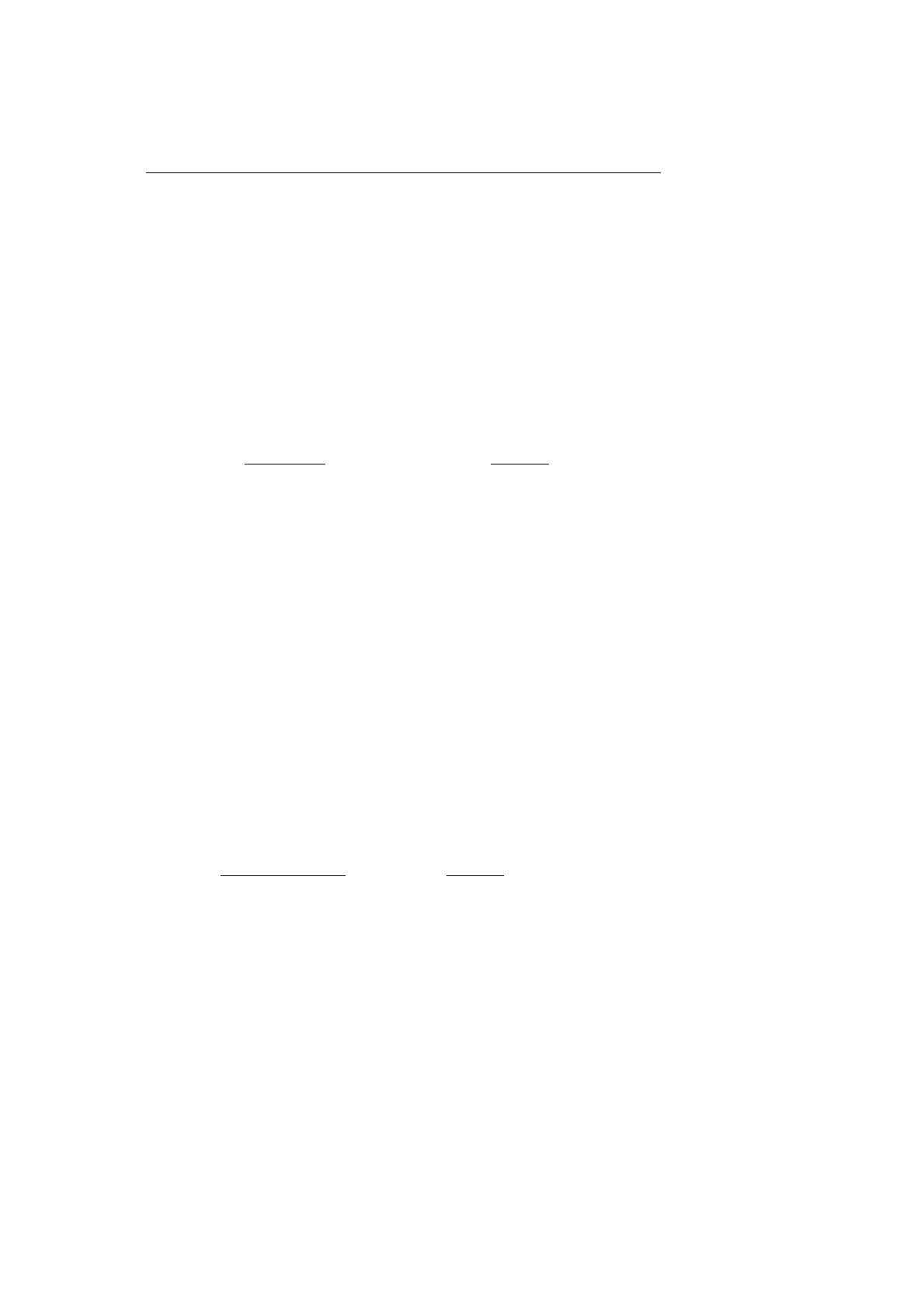
11.2. ПРАВИЛА ЕСТЕСТВЕННОГО ВЫВОДА

303

ности, в части 1, «Язык математики», разбиралось определение ра-

венства Лейбница, которое, по сути дела, устанавливает, что мы не име-

ем права пользоваться какими-либо свойствами,различающими равные

предметы. Здесь происходит аналогичное самоограничение.

Говоря,что объект

x произволен,мы лишаем себя права поль-

зоваться какими-либо ранее установленными фактами о дан-

ном объекте.

Правила, касающиеся квантора

∃, следующие:

Доказательство на примере:

A(y | t)

∃x A(y | x)

Вспомогательная константа:

∃x A(x)

A(c

n+1

)

Отметим две тонкости, которые есть в этих правилах. Во-первых, как

и в семантических таблицах, вспомогательная константа должна быть

девственной, отсутствующей и в нашей сигнатуре, и в ранее постро-

енной части вывода. Но использоваться она может лишь внутри того

вспомогательного вывода, в котором была введена. Когда этот подвы-

вод заканчивается, заканчивается и ее область действия. Во-вторых, в

правиле доказательства на примере подстановка должна прослеживать-

ся в обратном направлении, от результата к примеру. Так что не обяза-

тельно все вхождения терма t в посылку должны заменяться на связыва-

емую переменную x. В частности, корректен переход по этому правилу

от z = z к ∃x(z = x), поскольку z = z может рассматриваться как

результат подстановки z вместо y в z = y.

Правила для всеобщности следующие:

Обобщение: Переход от общего к частному:

∗ x произволен



∙∙∙

A(x

)

∀x A(x)

∀x A(x

)

A(x | t)

Во вспомогательном выводе правила обобщения нельзя пользоваться

никакими ранее появившимися формулами, содержащими x свободно.

Конечно же, выводы, касающиеся произвольной переменной x, делать

можно и нужно, но помогает при этом лишь правило перехода от обще-

го к частному: доказанное общее утверждение, содержащее y связанно,

304

ГЛАВА 11. ЕСТЕСТВЕННЫЙ ВЫВОД

может быть использовано при любом конкретном его значении, в том

числе и при x.

Рассмотрим пример доказательства с кванторами. Докажем фор-

мулу

∀x(A(x) ⇒ B(x)) & ∃x A(x) ⇒ ∃x B(x).

∗ ∀x(A(x) ⇒ B(x)) & ∃x A(x)



∀x(A(x) ⇒ B(x)) ∃x A(x)

A(c

)

A(c

) ⇒ B(c

)

B(c

)

∃x B(x)

∀x(A(x) ⇒ B(x)) & ∃x A(x) ⇒ ∃x B(x)

В этом доказательстве имеется единственная тонкость. Пока не по-

явилось c

, не стоит переходить от общего к частному, чтобы не ском-

прометировать эту константу преждевременно. Следующее доказатель-

ство напоминает наш первый пример из данной главы,но с добавлением

квантора всеобщности.

∗ ∀x(A(x) ⇒ B(x)) & ∀x(B(x) ⇒ C(x))



∀x(A(x) ⇒ B(x)) ∀x(B(x) ⇒ C(x))

∗ z

произвольно



A(z) ⇒ B(z)

B(z) ⇒ C(z)

∗ A(z)



B(z)

C(z)

A(z) ⇒ C(z)

∀x(A(x) ⇒ C(x))

∀x(A(x) ⇒ B(x)) & ∀x(B(x) ⇒ C(x)) ⇒ ∀x(A(x) ⇒ C(x))

В этом доказательстве интересно соотношение произвольных и не-

произвольных переменных. z объявляется как произвольное, остается

произвольным до того момента, когда открывается еще один подвывод,

в нем оно уже не произвольно, поскольку от него зависит допущение,

но после его завершения z вновь становится произвольным. Формулы

типа A(z) ⇒ B(z) не нарушают произвольности z, поскольку следуют

из посылок, не зависящих от значения z.

11.2. ПРАВИЛА ЕСТЕСТВЕННОГО ВЫВОДА

305

А вот следующий пример иллюстрирует типичную ошибку: мы “до-

кажем”, что поскольку все люди — мужчины или женщины, то все лю-

ди — мужчины или все люди — женщины.

∗ ∀x(A(x) ∨ B(x))



∗ x

произвольно



A(x) ∨ B(x)

∗ A(x) ∗ B(x)



A(x)

∀x A(x)

∀x A(x) ∨ ∀x B(x)



B(x)

∀x B(x)

∀x A(x) ∨ ∀x B(x)

∀x(A(x) ∨ B(x)) ⇒ ∀x A(x) ∨ ∀x B(x)

Здесь два структурных нарушения: во-первых, допущение, что x —

произвольно, используется не в том же подвыводе, а во вложенных, и

во-вторых, в этих вложенных подвыводах допущения уже зависят от x.

Если первое из нарушений хотя бы не противоречит самому духу систе-

мы, то второе, безусловно, противоречит всему.

Упражнения к § 11.2

11.2.1. Рассмотрите следующее исправление, внесенное в предыдущее

доказательство студенткой Примерной:

∗ ∀x(A(x) ∨ B(x))



A(x) ∨ B(x)

∗ A(x) ∗ B(x)



∗ x

произвольно



A(x)

∀x A(x)



∗ x

произвольно



B(x)

∀x B(x)

∀x A(x) ∨ ∀x B(x)

∀x(A(x) ∨ B(x)) ⇒ ∀x A(x) ∨ ∀x B(x)

11.2.2. Докажите следующие формулы:

A & (B ∨ C) ⇒ (A & B) ∨ (A & C).

2. (A & B) ∨ (A & C) ⇒ A & (B ∨ C).

3. A ∨ (B & C) ⇒ (A ∨ B) & (A ∨ C).

306

ГЛАВА 11. ЕСТЕСТВЕННЫЙ ВЫВОД

4. (A ∨ B) & (A ∨ C) ⇒ A ∨ (B & C).

5. (A ⇒ B ∨ C) & (C ⇒ D) & (B ⇒ ¬A) ⇒ (A ⇒ D).

(A & B ⇒ C) & (E ⇒ A) & (G ⇒ B) & (¬G ⇒ B) ⇒

(E ⇒ C).

7. (A & B ⇒ C ∨ D) & ¬D ⇒ (¬C & A ⇒ ¬B).

8. (A ⇒ B ∨ C) ⇒ (A ⇒ B) ∨ (A ⇒ C).

9. (A & B ⇒ C) ⇒ (A ⇒ C) ∨ (B ⇒ C).

10. (A ∨ B ⇒ C) ⇒ (A ⇒ C) & (B ⇒ C).

11. ((A ⇒ B) ⇒ A) ⇒ A.

12. ((A ⇒ B) ⇒ C) & ((B ⇒ A) ⇒ D) ⇒ C ∨ D.

11.2.3. Докажите следующие формулы:

∃x(A(x) & B(x)) ⇒ ∃y A(y) & ∃z B(z).

2. ∀x( A(x) ∨ B(x)) & ∃x ¬A(x) ⇒ ∃x B(x).

3. ∃x(A(x) ∨ B(x)) & ∀x ¬A(x) ⇒ ∀x B(x).

4. ∀x(A(x) ∨ B(x)) & ∃x(A(x) ⇒ C(x)) & ∀x(B(x) ⇒

C(x)) ⇒ ∃x C(x).

5. ∀x(A(x) ∨ B(x)) & ∀x(A(x) ⇒ C(x)) & ∀x(B(x) ⇒

D(x)) ⇒ ∀x(C(x) ∨ D(x)).

6. ∃y A(y) ∨ ∃z B(z) ⇒ ∃x(A(x) ∨ B(x)).

§ 11.3. ЕСТЕСТВЕННЫЙ ВЫВОД КАК ГРАФ

Здесь дается строгое определение естественного вывода через графы.

При этом выявляются еще два правила, обычно скрытые в традицион-

ной формулировке вывода как последовательности формул.

Прежде всего опишем типы вершин и ребер, присутствующих в гра-

фе вывода. Вершины делятся на формулы, описания, подвыводы и пра-

вила.Вершине-формуле приписывается формула;вершине-описанию —

переменная либо вспомогательная константа; вершине-правилу — на-

именование этого правила. Формулы и описания часто объединяются

под именем информационных вершин. Далее, ребра делятся на три ти-

па. Использующие выходят из информационной вершины или подвыво-

да и заканчиваются в правиле; порождающие — выходят из правила и

11.3. ЕСТЕСТВЕННЫЙ ВЫВОД КАК ГРАФ

307

заканчиваются в информационной вершине; структурные, или подчи-

няющие, — выходят из подвывода и заканчиваются в информационной

вершине или подвыводе. Среди структурных ребер выделяются ребра

допущение и результат. На структурные ребра накладываются следу-

ющие

Условия иерархии

1. Каждая информационная вершина является концом одного и толь-

ко одного структурного ребра.

2. Подграф,состоящий из подвыводов,является деревом.Корень это-

го дерева называется главным выводом.

3. В каждом подвыводе, кроме главного, начинается ровно одно ре-

бро “допущение”.В каждом подвыводе начинается ровно одно ре-

бро “результат”.

Таким образом, однозначно определяется подвывод, которому под-

чинена данная формула. Вершину, в которую ведет ребро “допущение”,

называют допущением данного подвывода; вершину, в которую ведет

ребро “результат”, — его результатом. Результат главного подвывода

называют теоремой. Формулы не могут быть связаны друг с другом не-

посредственно, они связываются посредством правил. Вершины, соеди-

ненные с правилом использующим ребром, называются посылками дан-

ного правила, а вершины, в которые входят порождающие ребра, — его

заключениями. Посылки используются данным правилом, а заключения

порождаются им. Структура взаимосвязи правил с информационными

вершинами и иерархией подвыводов описывается следующими услови-

ями:

Условия структуры

1. Каждая информационная вершина,кроме допущений,является за-

ключением одного и только одного правила.

2. Допущения не являются заключениями никакого правила.

3. Каждая информационная вершина, кроме результатов, использу-

ется не более чем одним правилом.

4. Результаты не используются никаким правилом.

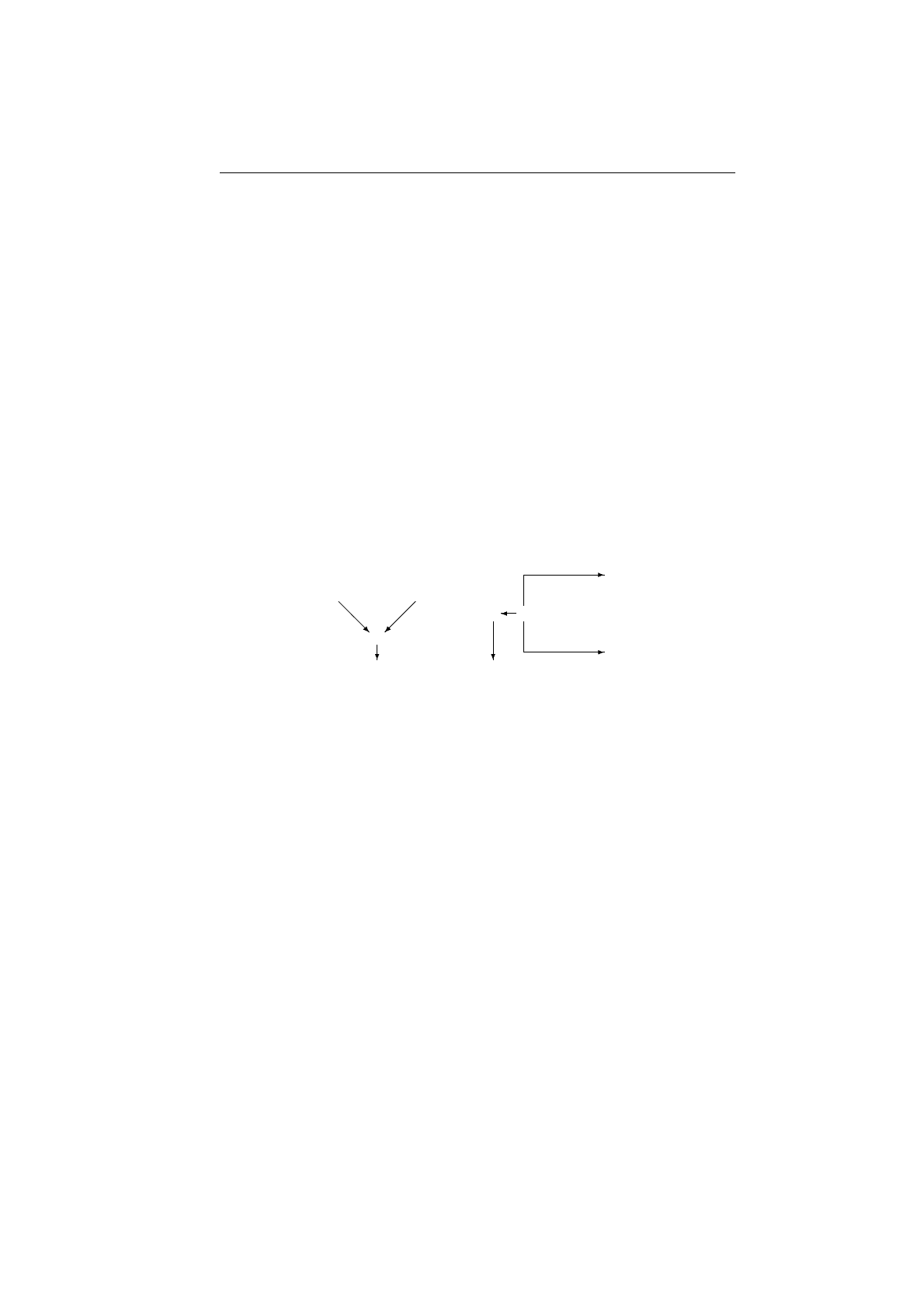
308

ГЛАВА 11. ЕСТЕСТВЕННЫЙ ВЫВОД

5. Посылки и заключения всех правил, кроме правила передачи ин-

формации, подчинены одному и тому же подвыводу.

6. Граф вывода не имеет циклов.

Итак, лишь правило передачи информации (ППИ) может перено-

сить формулы из одного подвывода в другой; все остальные действу-

ют строго внутри некоторого подвывода; данный подвывод называется

подвыводом правила.

Правила вывода описываются через их окрестности в графе вывода.

Эта окрестность включает посылки и заключения, а также допущения

и результаты посылок, если посылки являются подвыводами. Для пра-

вила передачи информации она включает также подвыводы, которым

подчинены посылка и заключение.

Опишем применения правил для импликации.

Modus ponens

•

A ⇒ B

•

МП ГП

◦

•

Правило дедукции

•

Допущение

Результат

•



◦

•

A ⇒ B

Здесь квадратик обозначает подвывод, кружочек означает правило. К

ребрам приписаны их типы. ‘МП’ означает малую посылку, ‘ГП’ —

главную посылку, ‘Допущение’ — допущение вспомогательного выво-

да, ‘Результат’ — его результат.

Правила для других связок описываются аналогично.

Дополнительным условием применения правила вспомогательной

константы является то, что вводимая в нем вспомогательная константа

отличается от любых констант, вводимых другими правилами. Далее,

вспомогательная константа не может входить в допущение или резуль-

тат соответствующего подвывода. Таким образом, она не может быть

вынесена наружу.

Еще два структурных правила вывода выделяются именно в гра-

фовом представлении, хотя имеют достаточно ясное значение и неявно

подразумеваются в традиционных определениях вывода. Это:

11.4. СОГЛАСОВАННОСТЬ С ИСТИННОСТЬЮ

309

Правило размножения

•

◦

•

. . .

•

Правило передачи информации

• •

 

◦

Первое из них имеет произвольное ( > 1) число заключений, повторяю-

щих ту же формулу, что была в посылке. Без него невозможно вывести

A ⇒ A, поскольку одна и та же вершина не может быть и допущением,

и результатом. Второе жизненно важно для взаимосвязи между подвы-

водами. На него накладывается следующее ограничение.

Передаваемая формула

A не может свободно содержать пе-

ременной,объявленной произвольной в подвыводе,куда она

передается.

Выводом называется граф, удовлетворяющий всем перечисленным

условиям и такой, что окрестность каждого применения правила имеет

соответствующий вид. Итак, правила задают условия на локальную пра-

вильность переходов, и она должна быть поддержана глобальной пра-

вильностью структуры вывода.

§ 11.4. ПРАВИЛА ФОРМУЛИРОВКИ ОТРИЦАНИЙ

И СОГЛАСОВАННОСТЬ

С КЛАССИЧЕСКОЙ ИСТИННОСТЬЮ

Приведем выводы ряда формул, доказываемых достаточно искусствен-

но, но необходимых для того, чтобы убедиться, что понятие естествен-

ного вывода действительно отражает классическую истинность. Далее,

их выводы позволят в дальнейшем „отделить овец от козлищ“: резуль-

таты, доказываемые прямо, от результатов, требующих косвенного до-

казательства от противного.

Прежде всего убедимся, что из заданных значений истинности со-

ставляющих формул следует истинность либо ложность сложной фор-

мулы. Например, A & ¬B ⇒ A ∨ B. Здесь, предположив A & ¬B

и получив из него A, по правилу ослабления можно немедленно выве-

сти A ∨ B. На самом деле ¬B оказывается просто ненужным. Столь

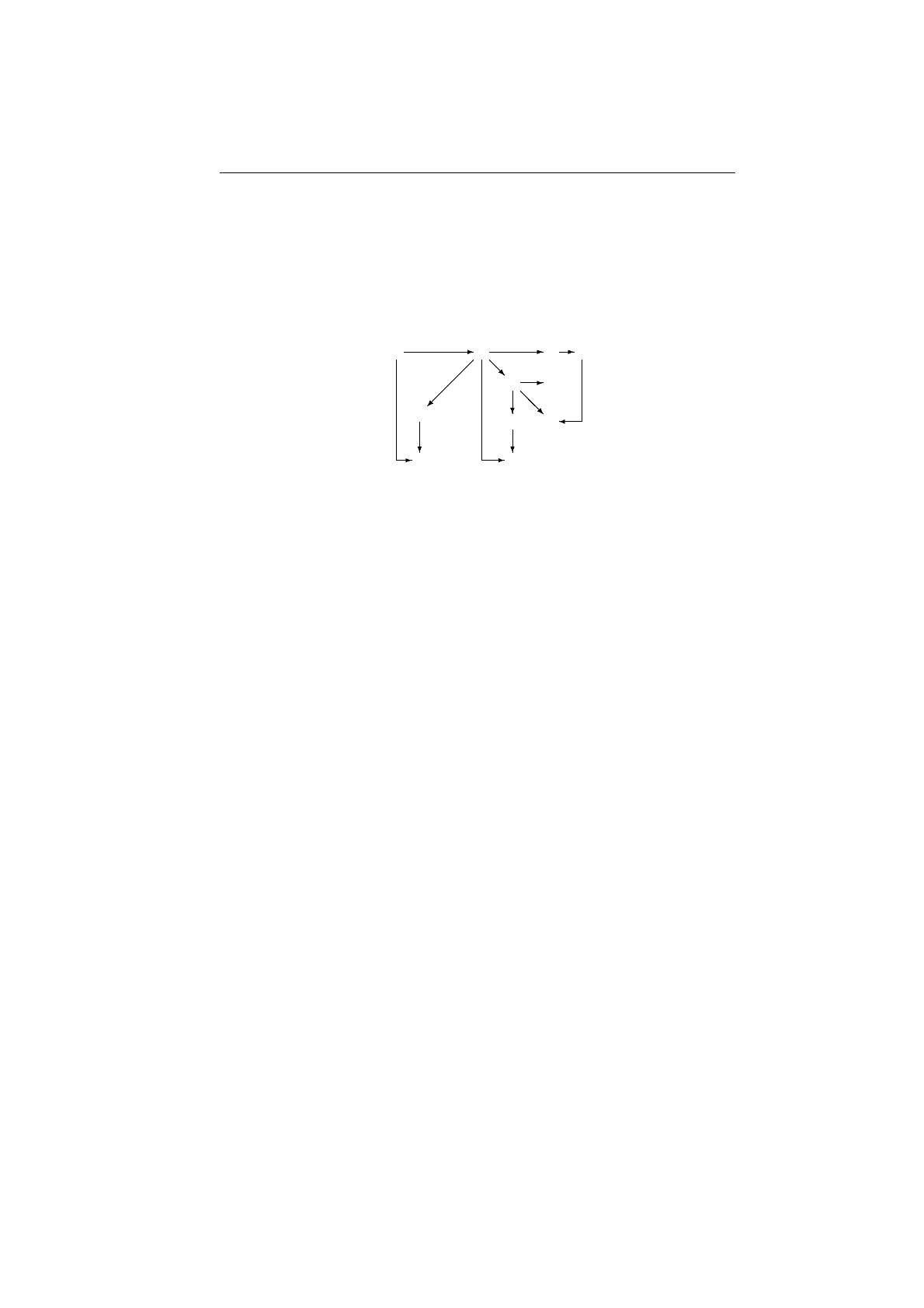
310

ГЛАВА 11. ЕСТЕСТВЕННЫЙ ВЫВОД

же тривиально доказывается B ⇒ A ∨ B. Далее, A & B ⇒ A &

B является тавтологией в любом смысле этого слова. Для установле-

ния ¬A ⇒ (A ⇒ B) достаточно воспользоваться правилом ex falso

quodlibet. B ⇒ (A ⇒ B) требует всего лишь аккуратного оформления,

которое и проделаем в виде графа:

 



Рез

•

B ⇒ (A ⇒ B)

◦

Рез

•

A ⇒

◦

•

Доп

◦

Доп

Рез

•

◦

Здесь видно, что во внутренний вспомогательный вывод с допуще-

нием B передается допущение внешнего вспомогательного вывода при

помощи правила передачи информации. Не намного труднее и доказа-

тельство ¬A ⇒ ¬(A & B). Здесь достаточно лишь корректно распоря-

диться правилом приведения к нелепости.

∗ ¬A



∗ A & B



⊥

¬(A & B)

¬A ⇒ ¬(A & B)

¬A

проносится во внутренний вывод при помощи правила передачи

информации. Интереснее вывод ¬A & ¬B ⇒ ¬(A ∨ B).

∗ ¬A & ¬B



¬A ¬B

∗ A ∨ B



∗ A ∗ B

|⊥ |⊥

⊥

¬(A ∨ B)

¬A & ¬B ⇒ ¬(A ∨ B)