Непейвода Н.Н., Скопин И.Н. Основания программирования

Подождите немного. Документ загружается.

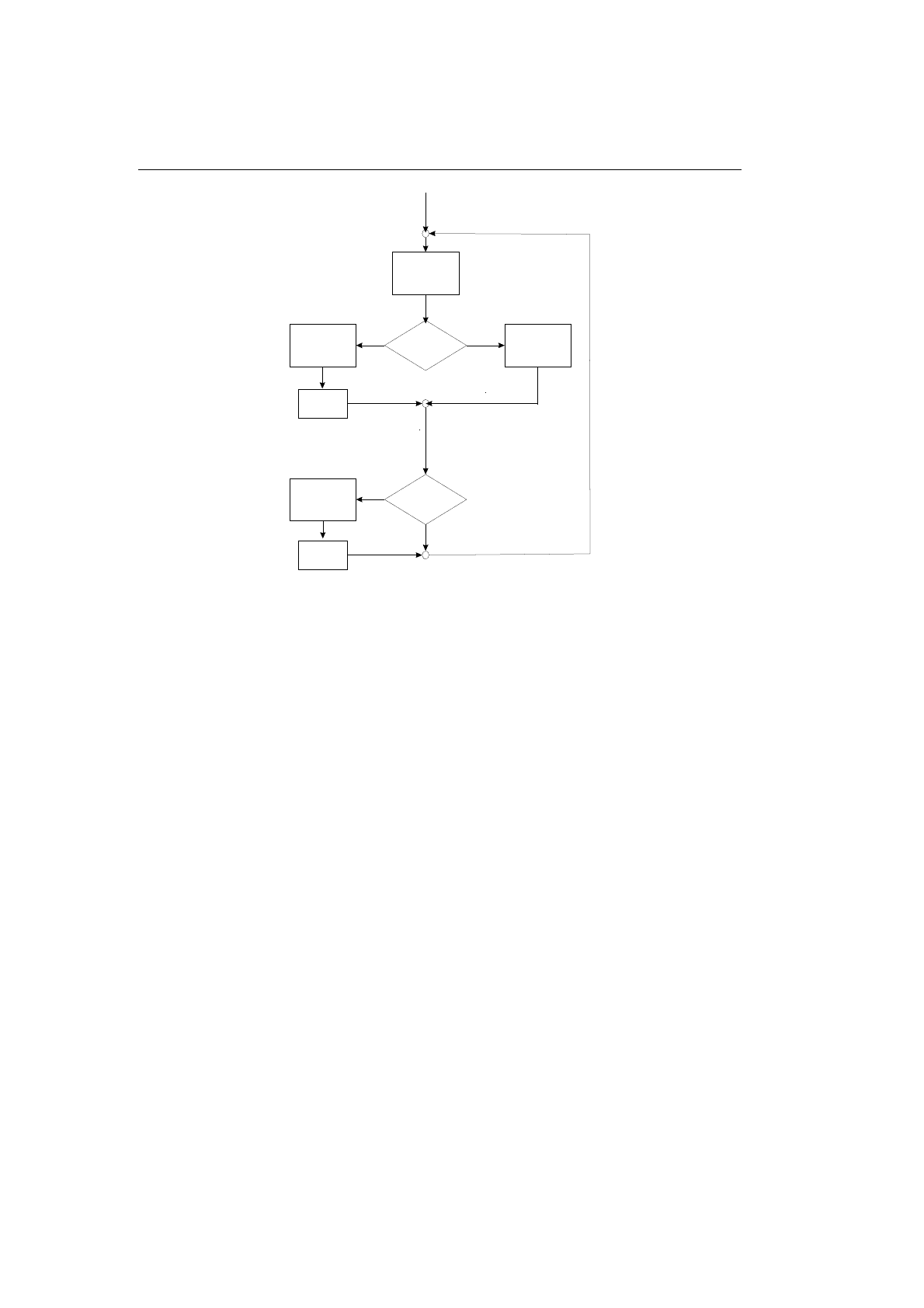
A.4. АВТОМАТЫ И МАШИНЫ ТЬЮРИНГА

845

Break

Рис. A.2. Структурирование цикла Бема-Джакопини

Конец определения A.3.1.

В схеме Янова присваивание обычно сокращается просто до f, и единствен-

ный параметр у предиката также опускается.

Для схем Янова разрешимо понятие функциональной эквивалентности

и имеется полная система функционально эквивалентных преобразований

этих схем. Однако перевести схему Янова в структурированную форму так,

чтобы она осталась схемой Янова, невозможно.

Более того, это не может быть преодолено добавлением структурных пе-

реходов на любое ограниченное число этажей иерархии вверх. Но после до-

бавления произвольных структурных переходов схемы Янова поддаются струк-

турированию (см. рис. A.2).

§ A.4. АВТОМАТЫ И МАШИНЫ ТЬЮРИНГА

Начнем с предельно абстрактного определения.

Определение A.4.1. Автомат A — отображение I × S → S. Множество I

называется множеством входных символов, множество S — множеством со-

846

ПРИЛОЖЕНИЕ A. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

стояний автомата. Автомат называется конечным, если множества входных

символов и состояний конечны. В множестве состояний выделяется некото-

рое состояние s

, называемое начальным состоянием автомата.

Конец определения A.4.1.

Если данное определение рассмотреть более операционально, то получаются

следующие трактовки:

a) Автомат — устройство, реагирующее на входные воздействия и меняю-

щее свое состояние в зависимости от предыдущего состояния и очеред-

ного входного воздействия.

b) Автомат — функция, преобразующая последовательности входных сим-

волов в последовательности состояний. Функция преобразования после-

довательностей Φ

определяется рекурсивно:

(a) Если Λ — пустая последовательность, то Φ

(Λ) = [s

(b) Если s — последний член Φ

(X), то

(X ∗ [a]) = Φ

(X) ∗ [A(a, s)].

(X) = lim

n→∞

([X

, . . . , X

]).

c) Автомат — устройство, читающее очередной символ из “последователь-

ного файла” входных символов и выдающее очередной символ в “после-

довательный файл” состояний. Решение автомата может зависеть от по-

следнего выданного символа.

Имеется еще одно, более ‘механическое’, представление конечного автомата.

Автомат —машина с центральным процессором, имеющим конечное число

состояний, одной входной и одной выходной лентами. И входная, и выходная

лента движутся каждый ход налево на один символ. Команды процессора

имеют вид

s : [a

, . . . , a

где s

— состояния, a

— символы входного алфавита, b

— символы выход-

ного алфавита. Это определение отличается от предыдущего тем, что автомат

может перекодировать пары

(

текущее состояние, входной символ

)

A.4. АВТОМАТЫ И МАШИНЫ ТЬЮРИНГА

847

в выходные символы. Наглядное представление работы такого автомата дано

на рис. A.3.

| | ... |a|...| |...

| | ... |b|...| |...

Рис. A.3. Автомат

В этой модели символ,помещаемый на выходную ленту, может интерпре-

тироваться как действие, выполняемое системой, формализацией которой

служит конечный автомат. Соответственно, символ на входной ленте может

пониматься как результат распознавания некоторых характеристик модели-

руемой системы некоторой системой предикатов.

Имеется одна вариация в определении конечного автомата, которая фор-

мально приводит к эквивалентному понятию, а на практике к другому ви-

ду программных представлений автоматных структур. До сих пор рассмо-

тренные формализмы допускали варьирование совершаемого автоматом дей-

ствия в зависимости от того, какой символ стоит на входной ленте (автоматы

Мура). В этом смысле действие является атрибутом не состояния, а перехода.

В программах часто действие выполняется до распознавания характеристик

и определения последующего перехода (автоматы Мили).

Множество называется автоматно разрешимым или регулярным

, если

оно представимо как множество таких последовательностей, для которых ко-

Последний термин часто встречается в литературе, мы им пользоваться не будем, по-

скольку вводить для каждого типа разрешимости свое слово — пережиток тех времен, когда

общей теорией вычислимости еще не занимались.

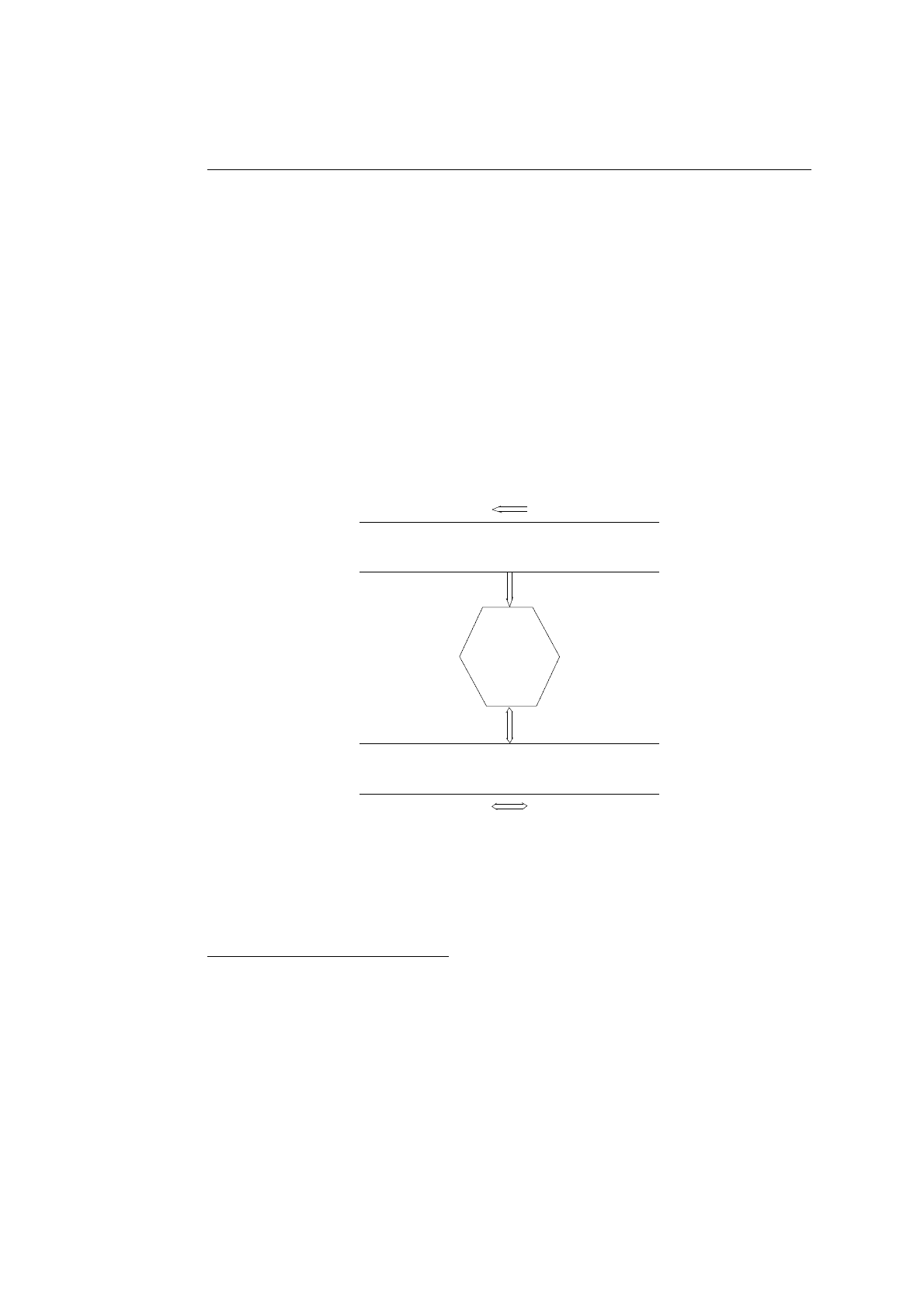
848

ПРИЛОЖЕНИЕ A. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

нечный автомат A переходит в одно и то же состояние. Автоматная разреши-

мость множества очень сильно зависит от кодирования его элементов. На-

пример, множество степеней двойки автоматно разрешимо лишь в таких си-

стемах счисления, основания которых сами являются положительными сте-

пенями двойки.

Если разрешить автомату не только писать на выходную ленту, но и чи-

тать с нее, и, соответственно, двигать ее в двух направлениях, то получается

модель вычислений, известная под названием машины Тьюринга. Машина

Тьюринга (в принципе) позволяет вычислить любую вычислимую функцию.

Поскольку принципы работы процессора машины Тьюринга подобны прин-

ципам работы процессора конечного автомата, программа машины Тьюринга

также часто задается таблицей переходов. Наглядное представление работы

машины Тьюринга дано на рис. A.4

| | ... |a|...| |...

| | ... |b|...| |...

Рис. A.4. Машина Тьюринга с оракулом

§ A.5. АЛГОРИТМЫ НАД СТРУКТУРАМИ

Для большего подчеркивания похожести моделей и одновременно решающих различий

между ними, мы изобразили на рисунке машину Тьюринга с оракулом: основное поня-

тие, используемое в тех случаях, когда изучается вычислимость относительно уже заданной

функции (записанной на входной ленте).

A.6. РЕКУРСИИ

849

Если рассматривать в качестве аргументов алгоритмов более сложные

структуры данных, то возникают другие понятия, в принципе сводимые к ма-

шинам Тьюринга, но представляющие самостоятельный интерес. Некоторые

из них уже послужили идейной основой интересных концепций программи-

рования, а другие еще ждут своего использования.

Прежде всего, рассмотрим понятие алгорифмов Маркова. Данными для

алгорифмов Маркова являются слова в произвольном конечном алфавите A.

Множество слов обозначим A

∗

. Элементарные действия — продукции вида:

a → b a → ·b

где a, b ∈ A

∗

. Такая продукция означает замену подслова a на подслово b.

Управляющая структура алгорифма Маркова в корне отлична от управля-

ющей структуры машины Тьюринга. Команды не имеют меток. Каждый раз

ищется первая из применимых команд и она применяется в первом возмож-

ном месте. Таким образом, неприменимо понятие состояния, в которой нахо-

дится исполняемая программа. Все определяется лишь состоянием памяти.

Если исполненная команда содержала точку либо ни одна из команд непри-

менима, исполнение завершается.

Рассмотрим пример. Алгорифм











ba → ab

ca → ac

cb → bc

→ ·

(A.1)

сортирует буквы в слове в алфавитном порядке. Последняя команда → ·при-

менима всегда, она введена для того, чтобы исполнение завершалось явной

остановкой, когда неприменимы существенные правила.

Заметим, что для другого алфавита алгоритм сортировки пришлось бы

переписать заново.

Еще одним нетрадиционным понятием алгоритма, также тесно связан-

ным (особенно в перспективе) с сентенциальным программированием слу-

жат алгоритмы Колмогорова.

§ A.6. РЕКУРСИИ

Еще одно определение алгоритма, принадлежащее Дж. Маккарти (автору,

в частности, языка

LISP

), лучше всего приспособлено для импортирования

850

ПРИЛОЖЕНИЕ A. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

типов данных, и, самое главное, концентрируется на важнейшем для про-

граммирования понятии рекурсивного описания системы функций и ставит

его в фундамент всей теории.

Входными данными и результатами алгоритма в данном случае являют-

ся списки. Они годятся для сочленения данных любых типов. Элементарные

данные естественно считать атомами, внутренняя структура которых неви-

дима для наших алгоритмов. Будем считать, что задано некоторое множество

атомов, обязательно включающее true и false Эти два атома будем называть

логическими значениями.

Определение A.6.1. Списки задаются следующим индуктивным определе-

нием.

1. Пустой список () (обозначаемый также nil) является списком.

2. Если l

,..., l

, n > 1 — атомы либо списки, то (l

, . . . , l

) — также

список.

Равенство списков задается следующим индуктивным определением.

1. l = nil тогда и только тогда, когда l также есть nil.

2. (l

, . . . , l

) = (k

, . . . , k

) тогда и только тогда, когда n = m и соответ-

ствующие l

= k

Конец определения A.6.1.

Таким образом, поскольку понятие, задаваемое индуктивным определением,

должно строиться в результате конечного числа шагов применения опреде-

ления, мы исключаем списки, ссылающиеся сами на себя, и списки в нашем

рассмотрении изоморфны упорядоченным конечным деревьям, листьями ко-

торых являются nil либо атомы. Списки считаются равными в том и только

в том случае, если у них одинаковое число членов и их члены равны.

Пример A.6.2. Все списки (), (()), ((())) и т. д. различны. Различны также и

списки nil, (nil, nil), (nil, nil, nil) и так далее. Попарно различны и списки

((A, B), C), (A, (B, C)), (A, B, C), где A, B, C — различные атомы.

Конец примера A.6.2.

Определение A.6.3. Элементами списка (l

, . . . , l

) называются l

, ..., l

Вершины списка L задаются следующим индуктивным определением.

A.6. РЕКУРСИИ

851

1. Элементы списка являются его вершинами.

2. Вершины элементов списка являются его вершинами.

Длиной списка называется количество элементов в нем. Глубиной списка на-

зывается максимальное количество вложенных пар скобок в нем. Соедине-

нием списков (l

, . . . , l

) и (k

, . . . , k

) называется список

, . . . , l

, k

, . . . , k

Замена вершины a списка L на атом либо список M получается заменой

поддерева L, соответствующего a, на дерево для M. Замена обозначается

L[a | M]. Через L[akM] будем обозначать результат замены нескольких вхо-

ждений вершины a на M.

Конец определения A.6.3.

Списки естественно изоморфны упорядоченным конечным деревьям, у ко-

торых листьями являются атомы и nil. Соответственно, появляются три чи-

словые характеристики списка. Длина списка — это количество членов в

нем. Глубина списка — наибольшая длина пути в дереве, задаваемом данным

списком. Ширина списка — наибольшее число вершин на одном из уровней

дерева.

Если мы стремимся определить в некотором смысле множество программ,

то нужно определить элементарные операции над списками (примитивы).

Как всегда, выбор их допускает некоторый произвол, но известные базисы

почти изоморфны. Мы выберем следующий базис из трех функций:

HD(x), выделяющая первый аргумент списка;

TL(x), выделяющая хвост списка x, т. е.

список без первого элемента;

ADD(a, x), добавляющая атом либо список

первым членом к x;

трех констант nil, true, false и четырех предикатов:

ATOM

проверяет, является ли x

элементом исходного множества U;

TRUE

проверяет, что x — атом, равный true;

FALSE

проверяет, что x — атом, равный false;

NULL

проверяет, что x — пустой кортеж [ ].

852

ПРИЛОЖЕНИЕ A. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Значениями предикатов считаются атомы true, false.

Пример A.6.4. Список (true, false, nil) выражается в нашем базисе как

ADD(true, ADD(false, ADD(nil, nil))).

Вообще,одноэлементный список с элементом A выражается как ADD(A, nil).

Конец примера A.6.4.

В связи с тем, что рассмотрено в предыдущем примере, вводится следующее

сокращение.

Выражение

ADD(t

, ···ADD(t

, nil) . . . )

обозначается

, . . . , t

)

Если мы желаем рассмотреть алгоритмы над некоторой алгебраической

системой Σ, то элементы ее носителя рассматриваются как атомы, вводит-

ся новый предикат, например, SIGMA(x), выделяющий среди атомов те, ко-

торые являются элементами Σ, а константы, предикаты и функции данной

алгебраической системы вводятся в число примитивов.

Внимание!

Поскольку равенство отнюдь не для всех типов данных является вычисли-

мым предикатом (например, равенство действительных чисел либо равен-

ство объектов никакого вычислительного смысла не имеет), мы не считаем,

что алгебраическая система обязательно содержит в числе элементарных

предикатов предикат равенства.

Мы не считаем, что все функции алгебраической системы Σ всюду опре-

делены (но предикаты, как правило, считаются всюду определенными).

Пример A.6.5. Если мы импортировали как алгебраическую систему поле

действительных чисел с обычными алгебраическими операциями, то следу-

ющее выражение

(HD(X) + HD(TL(X)))/HD(TL(TL(X)))

делит сумму первых двух элементов списка на третий. Конечно же, можно

было записать алгебраические операции как двухместные функции, но до

такого педантизма мы в данном изложении не дойдем. Тем не менее стоит

отметить, что, как всегда, сохранение привычных способов записи при до-

бавлении новых структур приводит к новым сложностям. Скобки вокруг ал-

гебраического выражения и скобки вокруг выражения, превращающие его в

одноэлементный список, становятся неразличимы.

Конец примера A.6.5.

A.6. РЕКУРСИИ

853

Термы, построенные из заданных известных функций, констант и предика-

тов при помощи перечисленных выше операций, называются простейшими

композициями.

Внимание!

Примитивные функции считаются неопределенными в тех случаях, которые

не заданы явно в их определении. Например, не определено значение HD(x),

если x является атомом или nil.Соответственно,функции,импортированные

из некоторой алгебраической системы, являются неопределенными, если их

аргументы выходят за пределы носителя этой системы. Предикаты же счи-

таются определенными, но ложными.

Таким образом, мы обошли проблему отсутствия типов данных в нашем

языке, просто описывая каждый тип данных своим предикатом. Это — стан-

дартный способ определения типов данных в логическом языке.

Определение A.6.6. Условные термы сигнатуры σ задаются следующим ин-

дуктивным определением.

1. Терм является условным термом.

2. Если P — n-местный предикат, t

, . . . , t

, r, s — условные термы, то

if P (t

, . . . , t

) then r else s ﬁ

также условный терм.

Выражение P (t

, . . . , t

) называется условием терма, а r и s — его альтерна-

тивами.

Конец определения A.6.6.

Значение условного терма вычисляется следующим образом. Вычисля-

ются значения всех аргументов предиката P . Если они оказались определе-

ны, то вычисляется значение P. Если оно оказалось истиной, то вычисляется

r, если оно оказалось ложью, то s. Итак, условные термы представляют из

себя просто условные выражения. При вычислении условного терма вычи-

сляется лишь одна из его альтернатив.

Логический условный терм определяется индуктивно.

1. Выражение P (t

, . . . , t

), где P — предикат, а t

, . . . , t

— произволь-

ные условные термы, является логическим условным термом.

854

ПРИЛОЖЕНИЕ A. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

2. Условный терм

if P (t

, . . . , t

) then r else s ﬁ

является логическим, если обе его альтернативы являются логически-

ми.

Аналогично можно дать определения условных термов любого данного типа,

только условия останутся логическими.

Без расширения класса вычислимых функций можно разрешить в каче-

стве условий термов произвольные логические условные термы. В самом де-

ле, результаты вычисления

if if P (t

, . . . , t

) then r1 else s1 ﬁ then r else s ﬁ

if if P (t

, . . . , t

) then if r1 then r else s ﬁ else

if s1 then r else s ﬁ ﬁ

совпадают.

С помощью условных термов можно дать определение всех логических

связок.

Определение A.6.7. Пополним сигнатуру σ конечным числом функциональ-

ных символов f

, . . . , f

арности соответственно m

, . . . , m

. Обозначим по-

лученную сигнатуру σ

Рекурсивная схема над σ — совокупность определе-

ний







, . . . , x

) ← t

, . . . , x

)

. . .

, . . . , x

) ← t

, . . . , x

)

(A.2)

где все t

— условные термы сигнатуры σ

, содержащие лишь переменные

, . . . , x

Конец определения A.6.7.

Таким образом, совокупность функций f

рекурсивно определяется сама че-

рез себя. Рассмотрим несколько примеров.

Пример A.6.8. Последний элемент списка.

LAST(x) ← if NULL(TAIL(x)) then HEAD(x) else LAST(TAIL(x)) ﬁ.

Конец примера A.6.8.