Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

402 Chapter

example, when the accuracy is nearly ideal, e.g. when the calculated rather

than the experimental Bragg angles are used to determine d*hkl, indexing is

usually straightforward and consistent even for large and low symmetry unit

cells. However, the presence of systematic errors combined with multiple

and sometimes severe overlaps of Bragg reflections (the latter are often

observed in complex crystal structures characterized by low symmetry, high

unit cell

volunle lattices) reduces the accuracy of peak positions and

therefore, decreases the chances of successful indexing from first principles.'

As established earlier (see section 2.8, Chapter 2), the interplanar

distances, d, are related to both the unit cell dimensions and Miller indices of

the families of crystallographic planes by means of a well defined function,

which in general form can be written as follows:

Peak positions,

€Ihkl, are measurable from a powder diffraction

experiment, for example using any of the approaches discussed in Chapter

Thus, the observed d-spacing for any given combination

(hkl)

is established

by means of the Braggs' equation, in which

is the wavelength used to

collect the data and

i.e. only the first order reflections are included

into the consideration:

d;;;

sin

8",;

By combining Eqs. 5.2 and 5.3, the observed positions of Bragg peaks

may be used to calculate the corresponding unit cell dimensions, but first,

the triplets of integer indices, h,

and

should be assigned to all observed

diffraction maxima or in other words, all observed Bragg peaks should be

indexed in agreement with Eqs. 5.1 to

5.3.

The algorithm of the indexing

process in powder diffraction is usually dependent on whether or not the

shape and dimensions of the unit cell are known at least approximately.

5.3

Known versus unknown unit cell dimensions

Indexing of powder diffraction data when unit cell dimensions are known

with certain accuracy includes:

Similar to structure solution from first principles, the

initio

indexing implies that no

prior knowledge about symmetry and approximate unit cell dimensions of the crystal

lattice exists. Indexing from first principles, therefore, usually means that Miller indices

are assigned based strictly on the relationships between the observed Bragg angles.

Unit cell determination and refinement

403

Generating a list of all possible combinations of symmetrically

independent

hkl

triplets, which can be observed within the studied range

of Bragg angles.

Calculating interplanar distances using the generated list of hkl, the best

estimate of the unit cell dimensions (a, b,

and

and the

appropriately simplified form of Eq.

5.2

(see Eqs. 2.29 to 2.34).

3. Assigning hkl triplets to the observed Bragg peaks based on the minimum

difference between ~P~%nd dcalchkl (or gobs and 9calchk~).

4. Refining the unit cell dimensions using 9•‹b~oupled with the assigned hkl

triplets,

i.e. using 0Ob$kl.

Although the indexing process may take several iterations, each resulting

in a more accurate assignment of indices and in a better approximation of the

unit cell, finding the best solution is usually trivial.

When both the symmetry of the lattice and unit cell dimensions are

unknown, the ab initio indexing of powder diffraction data often becomes a

trial-and-error process and finding the correct unit cell may be a challenge.

This occurs because the assignment of hkl triplets to each observed Bragg

peak is done without prior knowledge of the unit cell parameters (a total of

six in the most general case). Clearly, this task is equivalent to restoring the

directions of all observed reciprocal vectors based only on their lengths, so

to say one needs to restore a three-dimensional image from a single one-

dimensional projection. Referring to Figure 5.1, it is nearly as easy to obtain

the lower part of the figure from its upper part, as it is difficult to reconstruct

the latter if only the former is known.

The difficulty of the ab initio indexing may be further illustrated using a

non-crystallographic geometrical example by considering a cone, a cylinder

and a sphere, all of which have identical radii. Under certain conditions, it is

possible that their projections are reduced to identical circles in two

dimensions and then to indistinguishable lines in one dimension,' as shown

in Figure 5.2. Assuming that there is no additional information about these

objects and their projections, it is impossible to restore the correct shape of

the object in three dimensions based on a single one-dimensional projection.

The problem of indexing powder diffraction data is intricate but not as

hopeless as it may appear from Figure 5.2 due to the presence of governing

laws,

i.e. Eqs. 5.1 to 5.3. They define a set of rules for the reconstruction of

the reciprocal lattice, in which a vector of a given length may only realize a

limited number of orientations. The ab initio indexing is, therefore, possible

because vector directions should be such that their ends form a three-

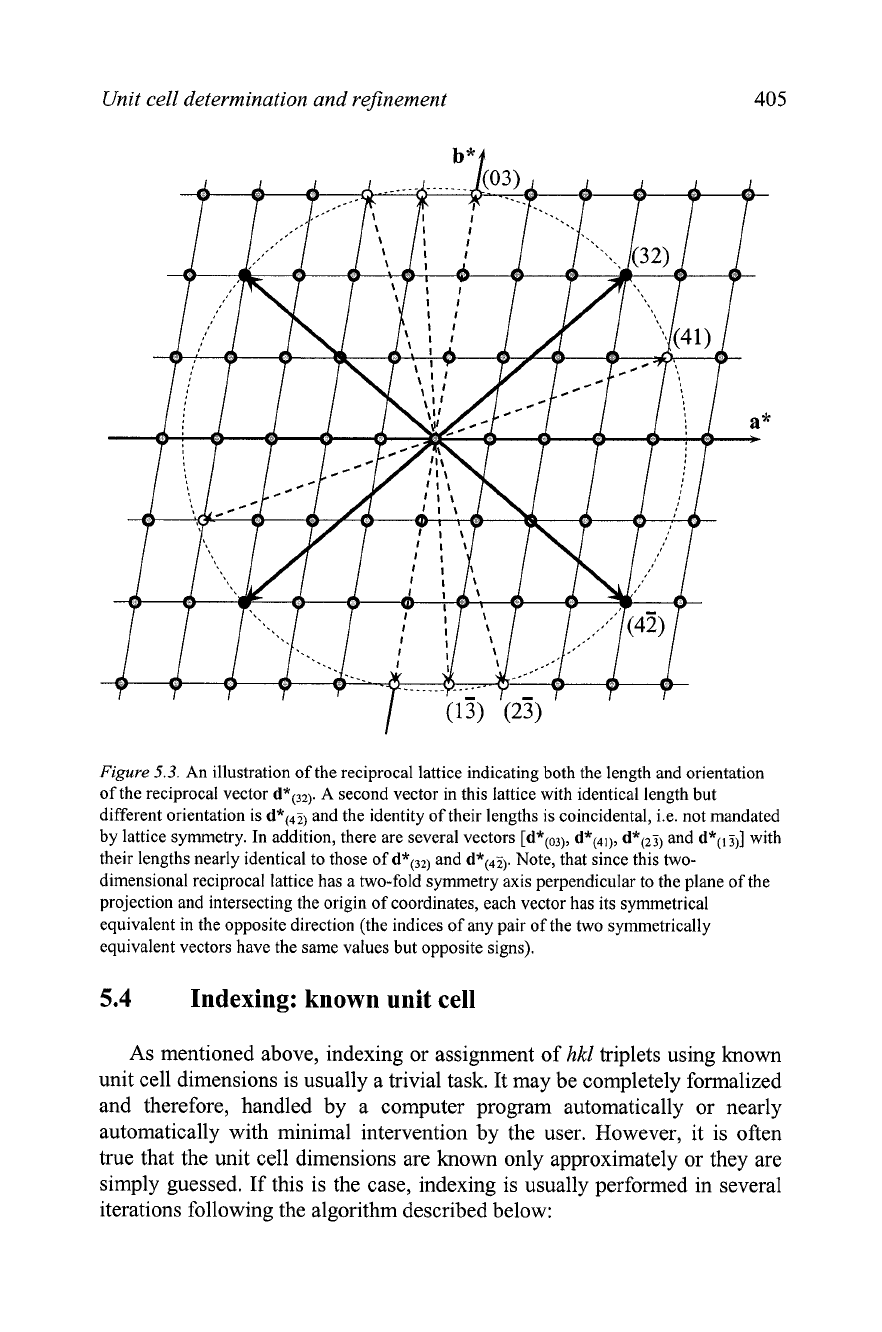
dimensional lattice. A two-dimensional example is found in Figure 5.3,

Strictly speaking, the shape of each figure could be restored from two-dimensional

shadows (projections) if the objects are semitransparent. Recognition becomes impractical

from one-dimensional projections.

404

Chapter

where the reciprocal lattice is identical to that shown in

Figure

5.1

and is

depicted with both the positive and negative directions of the two basis

lattice vectors

and

b*.

the absence of numerous overlapping Bragg peaks, which is the same

as the absence of numerous independent reciprocal lattice vectors with

identical lengths, the solution of the

ab initio

indexing problem is relatively

straightforward. This is, however, the case only in the highest symmetry

crystal system, i.e. cubic. As the symmetry of the lattice lowers, and

especially when the unit cell volume of the direct lattice increases, multiple

vectors with equal lengths but different directions will appear in the

reciprocal lattice, e.g. d*(32) and d*(45) where d*(32)

d*(4j) in

Figure

5.3.

Furthermore, numerous vectors will have nearly identical lengths but

different directions, e.g. d*@3), d*(41), d*(23) and d*(13) in addition to d*(32)

and d*(43. Since both the resolution of the instrument and the accuracy of

Bragg angle measurements are finite, the proper indexing of complex

powder diffraction

pattern(s) may be difficult or nearly unattainable from

first principles.

We conclude this section with a simple notion: it is impossible to solve

the crystal structure of a material using an incorrect unit cell. Thus, proper

indexing of the experimental powder diffraction pattern is of utmost

importance, and in this chapter we shall consider various strategies leading

to the solution of the indexing problem and how to find the most precise unit

cell dimensions.

Figure

5.2.

The illustration of three indistinguishable one-

and

two-dimensional projections

obtained from three different three-dimensional objects. The projection directions are shown

by dash-dotted arrows.

Unit cell determination and refinement

405

Figure

5.3.

An illustration of the reciprocal lattice indicating both the length and orientation

of the reciprocal vector

d*(32).

second vector in this lattice with identical length but

different orientation is

d*(',i)

and the identity of their lengths is coincidental, i.e. not mandated

by lattice symmetry. In addition, there are several vectors

[d*(03), d*(4,), d*(2j)

and

d*(,j,]

with

their lengths nearly identical to those of

d*(32)

and

d*(45).

Note, that since this two-

dimensional reciprocal lattice has a two-fold symmetry axis perpendicular to the plane of the

projection and intersecting the origin of coordinates, each vector has its symmetrical

equivalent in the opposite direction (the indices of any pair of the two symmetrically

equivalent vectors have the same values but opposite signs).

5.4

Indexing: known unit cell

As mentioned above, indexing or assignment of

hkl

triplets using known

unit cell dimensions is usually a trivial task. It may be completely formalized

and therefore, handled by a computer program automatically or nearly

automatically with minimal intervention by the user. However, it is often

true that the unit cell dimensions are known only approximately or they are

simply guessed. If this is the case, indexing is usually performed in several

iterations following the algorithm described below:

406

Chapter

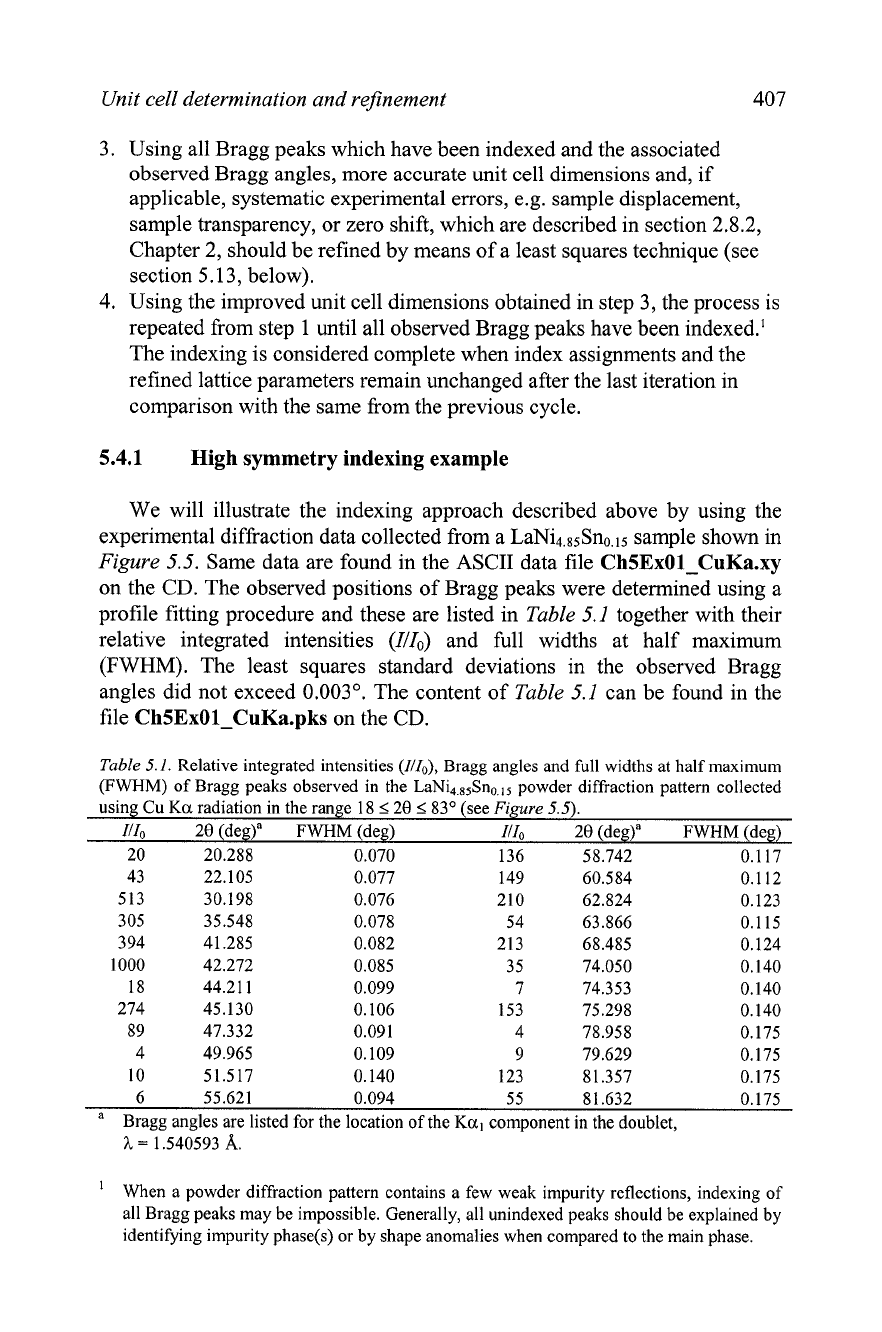
Expected Bragg peak positions, 2~~~'~hkl, shall be computed for all

possible combinations of Miller indices using the best available estimate

of the unit cell dimensions coupled with the appropriate form of

Eq.

5.2,

suitably simplified to reflect the symmetry of the reciprocal lattice. Only

those combinations of h, k and

that are allowed by symmetry of the

crystal lattice should be included in the calculations. The proper

computation process is illustrated by a flowchart in Figure

5.4.

When

available, Bragg peak positions coupled with known hkl triplets taken

from a literature reference or from a database

(e.g. the ICDD's Powder

Diffraction File') can be used instead of a computed list of 2eCalchk[.

2. Assignment of indices should always start from a peak observed at the

lowest Bragg angle and proceed towards the higher Bragg angles. The

low Bragg angle peaks are usually well resolved and are located far apart

from one another

(e.g. see Figure

5.1)

and therefore, it is relatively easy

to decide which triplet of indices corresponds to which observed peak.

The indexing should only continue as long as there is no ambiguity in the

assignment of indices.

Start

Yes

Figure

5.4.

The flowchart illustrating a generic algorithm designed to generate all allowed

combinations of Miller indices and compute ~ra& angles from known unit cell dimensions.

Only the values with

20Ca'chk,

not exceeding the maximum observed

are retained for further

use. Both minimum and maximum

and

values are calculated from the maximum

observed

20.

See section

4.4

in Chapter

and http://www.icdd.com/ for more information about the

Powder Diffraction File.

Unit cell determination and

refinement

407

Using all Bragg peaks which have been indexed and the associated

observed Bragg angles, more accurate unit cell dimensions and, if

applicable, systematic experimental errors,

e.g. sample displacement,

sample transparency, or zero shift, which are described in section 2.8.2,

Chapter 2, should be refined by means of a least squares technique (see

section 5.13, below).

Using the improved unit cell dimensions obtained in step

the process is

repeated from step 1 until all observed Bragg peaks have been indexed.'

The indexing is considered complete when index assignments and the

refined lattice parameters remain unchanged after the last iteration in

comparison with the same from the previous cycle.

5.4.1 High symmetry indexing example

We will illustrate the indexing approach described above by using the

experimental diffraction data collected from a LaNi4,85Sno.15 sample shown in

Figure

5.5.

Same data are found in the ASCII data file

Ch5ExOl-CuKa.xy

on the CD. The observed positions of Bragg peaks were determined using a

profile fitting procedure and these are listed in

Table

5.1

together with their

relative integrated intensities (IIIo) and full widths at half maximum

(FWHM).

The least squares standard deviations in the observed Bragg

angles did not exceed 0.003". The content of

Table

5.1

can be found in the

file

Ch5ExOl-CuKa.pks

on the CD.

Table

5.1. Relative integrated intensities (Ill,,), Bragg angles and

full

widths at half maximum

(FWHM) of Bragg peaks observed in the LaNi485Sno,15 powder diffraction pattern collected

using Cu Ka radiation in the range

83"

(see

Figure

5.5).

Ill,

(deg)a

FWHM (deg) IIIo

(deg)a

FWHM

(deg)

20 20.288

0.070

136 58.742 0.117

43 22.105 0.077

149 60.584 0.112

513

30.198

0.076

210 62.824 0.123

305

35.548

0.078 54 63.866 0.115

3 94

41.285

0.082

213 68.485 0.124

1000

42.272

0.085

3 5 74.050 0.140

18 44.2 1 1

0.099

7 74.353 0.140

274 45.130

0.106 153 75.298 0.140

89 47.332

0.091

4 78.958 0.175

4 49.965

0.109 9 79.629 0.175

10 51.517

0.140 123 8 1.357 0.175

6 55.621

0.094 5 5 8 1.632 0.175

Bragg angles are listed for the location of the

Ka,

component in the doublet,

1.540593

When a powder diffraction pattern contains a few weak impurity reflections, indexing of

all Bragg peaks may be impossible. Generally, all unindexed peaks should be explained by

identifying impurity

phase(s) or by shape anomalies when compared to the main phase.

Chapter

LaNi

,,,,

,,,,,

20 25 30 35 40 45 50 55

65 70 75 80

Bragg angle,

(deg.)

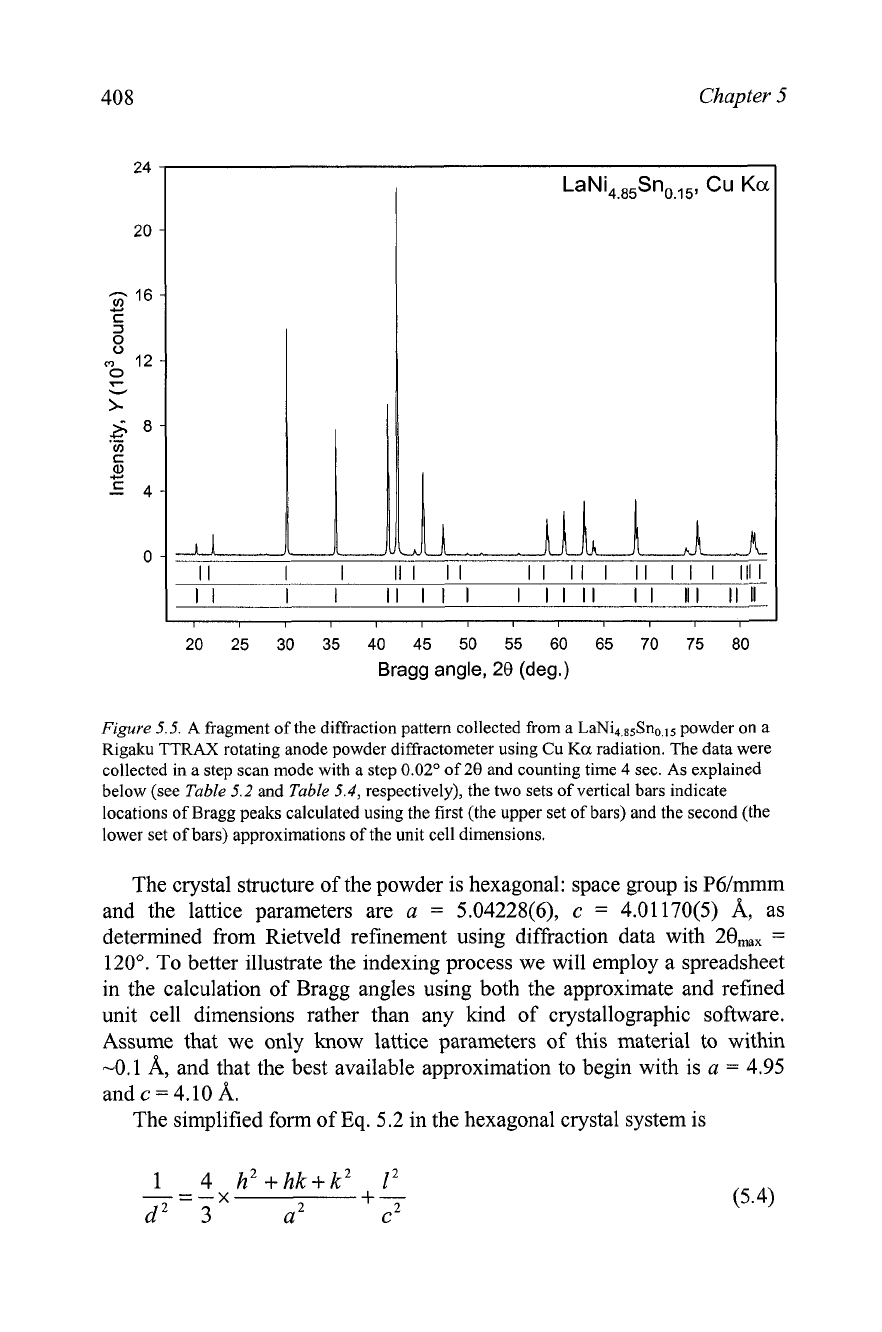
Figure

5.5.

A fragment of the diffraction pattern collected from a LaNi4 85Sno

powder on a

Rigaku TTRAX rotating anode powder diffractometer using Cu

Ka radiation. The data were

collected in a step scan mode with a step

0.02"

and counting time

sec. As explained

below (see

Table

5.2

and

Table

5.4,

respectively), the two sets of vertical bars indicate

locations of Bragg peaks calculated using the first (the upper set of bars) and the second (the

lower set of bars) approximations of the unit cell dimensions.

The crystal structure of the powder is hexagonal: space group is P61mmm

and the lattice parameters are

5.04228(6),

4.01170(5) A, as

determined from Rietveld refinement using diffraction data with 20,,,

120'. To better illustrate the indexing process we will employ a spreadsheet

in the calculation of Bragg angles using both the approximate and refined

unit cell dimensions rather than any kind of crystallographic software.

Assume that we only know lattice parameters of this material to within

-0.1 A, and that the best available approximation to begin with is

4.95

andc=4.10

The simplified form of

Eq.

5.2 in the hexagonal crystal system is

Unit cell determination and refinement

409

After combining Eqs.

5.4

and 5.3 we get the following equation relating

Bragg angles, lattice parameters and Miller indices:

To ensure that no possible combination of indices have been missed (see

Figure

5.4) it is best to create a spreadsheet, in which the columns are

labeled with values of

varying from

ldn

-1,,

I,,,,,.

The value of

Inlax

determined from Eq.

5.5

by substituting 28,,, for 28 and letting

The rows are labeled with the values of

and k.

general, both

and k

should vary between their respective minimum and maximum values

determined in the same way as

ld,

and

I,,,,,.]

the hexagonal crystal system,

however, there is no need to include negative values of indices due to

limitations imposed by symmetry of the reciprocal lattice, and the smallest

values of all three indices are set at 0. Furthermore, reciprocal lattice points

that are different from one another by a permutation of

and k are

symmetrically equivalent in this hexagonal lattice. As a result, we have an

additional restriction, i.e.

k (or

k) that limits the possible

combinations of indices. No other limitations are imposed on the allowed

combinations of indices in the case of LaNi4.85Sno.15, since the space group

symmetry of the material is

PGImmm, which according to

Table

2.15, has no

forbidden reflections.

The spreadsheet, used to calculate

Table

5.2, may be found on the

CD,

the file name is

Ch5ExOl~BraggAngles.xls.

The calculated Bragg peak

positions from

Table

5.2 are plotted as the upper set of vertical bars in

Figure

5.5. It is easy to recognize that only four lowest Bragg angle peaks

can be decidedly indexed using the first approximation of the unit cell

dimensions. The corresponding assignment of the triplets of indices is shown

Table

5.3, which is the result of combining the experimental data listed in

Table

5.1 with the calculated Bragg peak positions listed in

Table

5.2.

Based on the results of the first round of indexing the least squares

refinement of the lattice parameters yields the following values:

5.047(1), c

4.017(2)

The recalculated Bragg angles are shown in

Table

5.4 and they are plotted in

Figure

5.5 as the lower set of vertical bars. It is

clear that nearly all observed Bragg peaks may now be unambiguously

indexed as shown in

Table

5.5, where all differences between the observed

more precise definition of

Ih,,l, Ik,,\

and

Il,,I

can be given in terms of the maximum

reciprocal lattice vector length, which is

Id*hkllmax

211.

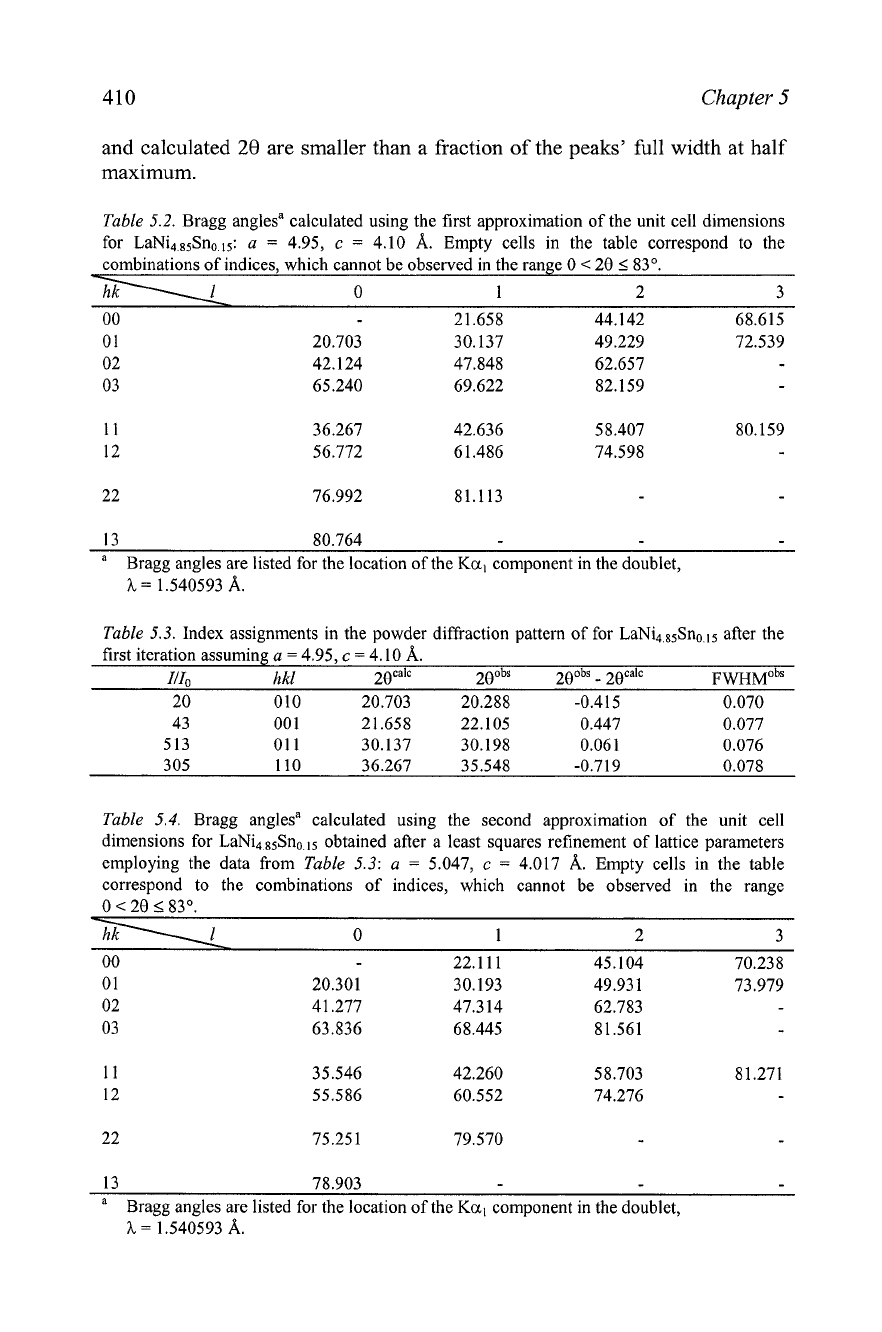
410

Chapter

and calculated

are smaller than a fraction of the peaks' full width at half

maximum.

Table

5.2. Bragg anglesa calculated using the first approximation of the unit cell dimensions

for LaNi4,85Sno.ls:

4.95,

4.10

Empty cells in the table correspond to the

combinations of indices, which cannot be observed

the range

83".

-1

80.764

Bragg angles are listed for the location of the Ka, component in the doublet,

1.540593

Table

5.3. Index assignments in the powder diffraction pattern of for LaNi4,85Sno.15 after the

first iteration assuming

4.95,

4.10

hkl

2g~al~ 280bS 2gob~

2g~al~

FWHMO~

20 010 20.703 20.288 -0.415 0.070

Table

5.4.

Bragg anglesa calculated using the second approximation of the unit cell

dimensions for LaNi4,8sSno.15 obtained after a least squares refinement of lattice parameters

employing the data from

Table

5.3:

5.047,

4.017

Empty cells in the table

correspond to the combinations of indices, which cannot be observed in the range

28 583'.

Bragg angles are listed for the location of the Kal component in the doublet,

1 .NO593

Unit cell determination and refinement

41 1

Table

5.5.

Assignment of indices after the unit cell dimensions of LaNi,,,5Sno,15 have been

refined using four lowest Bragg angle peaks:

5.047,

4.017

Illo

hkl

2ecalc

200b

2e0by

2ecalc

FWHMO~~

20 010 20.301 20.288 -0.013 0.070

032

1.632 0.071 0.175

The

1 11

Bragg reflection of

impurity phase (a solid solution of Sn in Ni).

The

002

Bragg reflection of an impurity phase

solid solution

Sn in Ni).

A least squares refinement of the unit cell dimensions of LaNi4,85Sno,15

based on the observed Bragg angles and indices listed in

Table

5.5 yields the

following unit cell:

5.042 1(1), c

4.0 1 18(l)

The lattice parameters

have been refined together with a zero shift correction, which was

determined to be 0.032". The final indexing of this diffraction pattern is

shown in

Table

5.6, where the observed Bragg angles have been corrected

for the zero shift error by adding 0.032" to each observed 20.

There are two weak Bragg peaks in this diffraction pattern, which could

not be indexed since they do not belong to the hexagonal crystal lattice with

the established unit cell. As we will find out later (Chapters

and

7),

these

two peaks manifest the presence of a small amount of an impurity phase

solid solution of Sn in Ni, which has a face-centered cubic crystal structure

with the space group symmetry Fm3m and

3.543

Only one

theoretically possible Bragg peak of the major hexagonal phase (003) is

unobserved in this powder diffraction pattern because its intensity is below

the limits of detection.