Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

Thermodynamics of Continuous Media 73

3) Mixed condition: where a linear relationship exists between the wall flux-

density and the temperature difference between the wall temperature T

(M) and

a given temperature T



)( TTh



The coefficient h of the above relation is called the heat-transfer coefficient

of the wall. It can represent diverse phenomena, such as an external wall, heat

transfer across the boundary layer of a flowing fluid, etc.

Furthermore, as we have already said, it is necessary to fix the initial

temperature distribution in the domain being studied.

In addition to a detailed knowledge of temperature fields, other important

unknown quantities are:

– either the wall heat-flux-density and the thermal power issuing from the

domain studied when the wall temperature is given;

– or the wall temperature in the case where the heat-flux wall is given.

Finally, in the case where chemical reactions occur at the boundary

(evaporation, fusion, catalytic reactions, oxidation, electrolytic reactions, etc.),

we have more complex conditions. So, it is often at the boundary that heat is

released (positively or negatively) with a power proportional to the speed of a

reaction. As the reaction is often limited with respect to the transfer towards the wall

of certain reactants present in the fluid, we have a coupling between a thermal

problem and a problem related to the diffusion of the fluid constituents in which the

presence of flows plays an essential role. For example, in evaporation of a wet wall

in an air flow (temperature measured by a wet-bulb thermometer), the quantity of

liquid evaporated and heat absorbed in the wall surface are increasing functions of

the flow velocity, but the wall temperature is quite independent of the flow velocity

([BIR 01]).

2.4. Diffusion

2.4.1. Introduction

2.4.1.1. Definition

When a fluid F

is carefully introduced to a recipient which contains a fluid F

which is miscible with F

, after a certain duration we notice that movements related

74 Fundamentals of Fluid Mechanics and Transport Phenomena

to mixing have ceased, and that hydrostatic equilibrium is attained; however, an

inhomogeneity can persist in the concentration (this can be observed by differences

in color for example). This indicates that the phenomenon is an extremely slow

function of time. This migration of the components with respect to one another

constitutes a phenomenon known as material diffusion which is characterized by the

fact all of the components of a mixture do not have exactly the same speed, and

these differences lead to variations in the composition of the mixture.

The molecular velocity of a body of given chemical species which makes up a

mixture is thus engendered by two causes: the diffusion and the bulk movement of

the mixture (convection). The separation of these two causes must be very carefully

considered, as the bulk movement results from the behavior of all of the

constituents. Interactions between the two kinds of phenomena (convection and

diffusion) are encountered in all mixing processes with or without chemical

reactions (for example, sugar, which dissolves in coffee).

2.4.1.2. Microscopic interpretation of diffusion

This difference in the behavior of the two components is obviously related to

molecular agitation, which leads to a macroscopic displacement and is different for

the two components. The molecular agitation can be directly visible under certain

conditions in the presence of very small particles (in the order of a few micrometers)

in suspension in a fluid. Examined under a microscope these particles present erratic

behavior: this is known as Brownian movement, which is a macroscopic

manifestation of molecular agitation. These movements obey diffusion equations.

Let us consider two molecular species (black and white molecules in Figure

2.9a). By supposing that the two categories of molecules have the same energy (in

other words the same temperature), each molecular species moves as a result of

collisions. These collisions have a random character; for a resting gas made up of

one or many species of molecule, uniformly distributed, we see that the molecules

are statistically stationary, because each species only permutes between themselves.

During collisions and molecular interactions in the volume shown in Figure 2.9a,

there are more black (or respectively white) molecules at the bottom (or at the top),

but they will end up uniformly distributed in the container considered. The statistical

aspects of the second principle of thermodynamics leads to a complete mixing of the

two species, whose concentrations become uniform.

However, in this container, where the pressure is supposed constant, the total

molar concentration remains constant at all points, with the species whose

concentration decreases being replaced by the other species whose concentration

increases. This pressure constraint leads to a relation between migrations of the two

species.

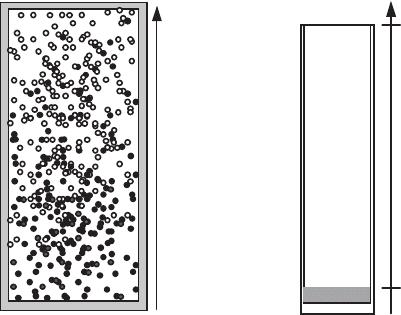
Thermodynamics of Continuous Media 75

(a) (b)

Figure 2.9.

(a) Gaseous diffusion in a volume; (b) evaporation of a liquid

Evaporation towards the atmosphere of a liquid contained in a tube (Figure 2.9b)

is another example of gaseous diffusion where we have a vapor flux from the liquid

towards the exterior across air, which is at rest in the tube. Note that the vapor

crosses the free surface of the liquid (at the lower wall where evaporation takes

place) and diffuses towards the exterior air, whereas the air, which does not dissolve

in the liquid, does not cross the free surface.

For the sake of simplicity, we will consider the case of mixing between two

perfect gases: gravity here often plays a negligible role at the laboratory scale.

Kinetic gas theory allows the modeling of phenomena at the molecular scale. We

will limit the discussion to cases where the temperature of the systems studied is

uniform; if this was not the case, it would be necessary to introduce a further

phenomenon: thermal diffusion. The interested reader should refer to classic texts on

the subject (see section 2.4.5).

It should nevertheless be noted that, depending on the problem studied, the

influence of external forces or accelerations on diffusive phenomena should be taken

into account (centrifugation for example).

2.4.1.3. Extensive variables of a mixture

The composition of a continuous medium where k chemical species are present

can be characterized by the local reduced extensive concentration variables which

can be either:

76 Fundamentals of Fluid Mechanics and Transport Phenomena

 the number of moles n

of each species per unit volume (molar

concentration);

 the partial density

of the species i, which is the mass per unit volume

(

iii

) of the molecules of species i, of molar mass M

(mass

concentration);

 the partial pressure p

i associated with the molecules of species i supposed

only to occupy an elementary local volume of the mixture.

As the preceding quantities are additive, we can define the total number of moles

n (or molecules) per unit volume, and the density

of the mixture:

¦¦¦

Mnnn

111

;

[2.20]

If the system comprises a perfect gas, which we assume in what follows, the

total pressure is equal to the sum of the partial pressures of the different

constituents.

We also consider the concentrations of the species i by means of relative values:

– molar fraction

;

– mass fraction

;

[2.21]

According to [2.20], these variables respect the relations:

1;1

¦¦

While the density

or the number of moles n per unit volume of a mixture

appear in the global mixing equations, the composition of the mixture is in fact

characterized by the given concentrations of only k  1 components.

In a liquid medium, the molar concentration C

(also called molarity) is

expressed as the number of moles of a species contained in a volume equal to 1 liter.

It often happens that the mixture contains a constituent 1, which is dominant, and

a weak proportion of a species i:

Thermodynamics of Continuous Media 77

111

or: or: ....

iii

nn pp   

All relative concentrations of species 1 then have the same first order value. For

example, it is thus possible to confuse the molar fraction

= n

/ n with the quantity

= n

/ n

, the errors thus committed being in the order of (n

/ n

)

. The same goes

for the mass fraction

and the quantity

, the partial pressure p

/ p

and p

/ p

. All these variables of relative concentration are proportional. We will

note as c

the species concentration i present in small quantities in a mixture.

2.4.2. Molar and mass fluxes

2.4.2.1. Flux of a component

We have seen (see section 2.1.3.1) that for any scalar extensive quantity G, we

can identify a corresponding vector flux density

, whose flux across the surface

(S) (equation [2.3]) represents the quantity of G which crosses S per unit time. The

extensive quantities of a pure body (volume, energy, etc.) are associated with the

matter which we suppose fixed in the reference frame. In the presence of diffusion,

not only does this reference not exist, but the flux densities of the components, as a

result of their movement, depend on the particular reference which is chosen. We

will return to this choice at a later stage...

It can easily be seen that the matter which crosses a surface ds at a velocity

over a period of length

G

t, comprises a cylinder of length

whose volume is

equal to

V.n į t.

Figure 2.10.

Balance in an elementary displacement across ds

78 Fundamentals of Fluid Mechanics and Transport Phenomena

Letting

be the volume density of the quantity G (see section 2.1.1), we can

derive expressions for the vector flux density

of G

and the flux

of the

quantity

G across the surface S:

³³

GGSg

dsnVgdsnqVgq

By considering

to be the number of moles per unit volume, we obtain

respectively for the

molar flux density

and the molar flux

across (S) of the

constituent

i with velocity

³³

nniii

dsnVndsnqVnq

..;

[2.22]

If we now choose mass to be the extensive quantity, we obtain, respectively for

the mass flux density

and the mass flux

of the component i across (S):

³³

mimiiimi

dsnVdsnqVȡq ...

 [2.23]

The molar flux

and the mass flux

represent, respectively, the number

of moles and the component mass i crossing S per unit time.

2.4.2.2. Balance equations

The balance equation of each constituent i (i =1, 2,…, k) can be obtained by

applying equation [2.8] to the volumic number of moles n



nini

nij

qdiv

The volume source

is the (volumetric) volumic number of moles in

component i created by homogenous chemical reactions. By replacing the molar flux

density with expression [2.22]:



.,..2,1 kiun

niiji



[2.24]

2 We shall study convective fluxes in more detail later (section 3.3.3.2).

Thermodynamics of Continuous Media 79

Balance equations can be written for the density

, which are equivalent to

[2.24], by multiplying each of these by the molar mass M

of the corresponding

component:



.,..2,1 kiMu

niiiji



[2.25]

2.4.2.3. Global fluxes and mean velocities

For the set of components of a mixture, we define:

– the total density

of the molar flux and the total molar flux

inn

Vnqq

¦¦

dsnq

[2.26]

– the

total density

of the mass flux

and the total mass flux

imm

Vqq

¦¦

dsnq

[2.27]

The global molar and mass balances for the mixture allow average mixing

velocities to be defined according to the methodology described in section 1.4.2.5

for the intensive quantities

. We thus define:

– the

molar average velocity

(which is independent of the molar mass) using

the molar balance [2.26]:

[2.28]

– the

mass average velocity

(velocity of the inertia center of a fluid particle

using mass balance [2.27]:

[2.29]

where

iii

is the partial density of the species i of molar mass M

3 The velocity is an intensive quantity (see section 1.2.1).

4 See section 3.2.1 and following sections.

80 Fundamentals of Fluid Mechanics and Transport Phenomena

The velocities

and

are the same only if the continuous medium comprises

a homogenous mixture of constant composition or of identical molecules (a pure

substance).

The molar fluxes

and

represent, respectively, the number of moles and

the total mass of a mixture which are crossing a surface

S per unit time:

³³

dsVndsq ..

³³

dsVdsq ..



By summing equations [2.24], term by term, and taking account of definition

[2.28], we obtain the balance equation for the total volumic number of moles





Vndiv

[2.30]

The quantity

is the number of moles created by chemical reactions.

We do the same for equations [2.25] and [2.29]; however, the sum

nii

zero as there is no mass source. We obtain the conservation equation for the total

mass:



0 

Vdiv

[2.31]

We will encounter the preceding equation again in the next chapter, during our

study of fluid flows, where it plays a fundamental role.

The reader will note that the

k equation [2.24] (or [2.25]) is equivalent to the

system of

k-1 equation [2.24] (or [2.25]) and equation [2.30] (or [2.31]). In other

words, it suffices to describe

k-1 component balance equations in addition to the

global balance equation for the mixture.



2.4.3. Choice of reference frame

2.4.3.1. Introduction

In this chapter, we have already studied the transfer of diverse quantities G

(energy, entropy, etc.) with respect to matter which was supposed stationary; in

Thermodynamics of Continuous Media 81

Chapter 3 we will examine the transport of a quantity G associated with convection

of matter, in other words associated with a bulk movement of the continuous

medium.

In an inhomogenous mixture, each component

i has its own velocity

. There is

therefore no preferred reference frame in which all of the matter is stationary. It is

for this reason that we did not specify the reference frame used in the preceding

definitions of flux.

As diffusion is a

differential phenomenon between the components, it is

necessary to identify a global condition which defines the bulk movement of the

matter, in other words it is necessary to fix the local mean velocities field for the

matter, as diffusion is a phenomenon which must be considered relative to a mean

velocity. The reference frame chosen for a study of diffusion is thus determined by

the choice of reference frame for the mean velocity. It depends on the kind of

problem studied, as the following examples demonstrate.

The quantities which characterize diffusion (velocities, flux densities), which

depend on the reference frame

R chosen for their study, will be represented between

brackets

with a superscript (*,G or 1) indicating the reference frame.

2.4.3.2.

Diffusion in a fluid at mechanical rest

Let us now consider an isothermal fluid mixture containing k components.

Diffusion phenomena are here characterized by very slow velocities associated with

negligible accelerations. The local composition is characterized by the number of

moles

per unit volume for each species. Suppose that the total number of moles n

per unit volume is constant at all points in the mixture (for example, in an ideal

isothermal gas). In the absence of chemical reactions, equation [2.30] can thus be

written:

Vdiv

[2.32]

We will limit our discussion to a simple case involving a configuration in stable

equilibrium (section 2.2.1.6), in which the concentration is constant in horizontal

planes, the diffusion velocities being vertical and parallel to the axis Ox. The field



txV

, which thus respects the condition

dxdV

, derived from [2.32], is

uniform at each instant and the molar average velocity



is only a function of

time.

The preceding situation is observed for isothermal gaseous mixtures whose

pressure is uniform and constant. In a gravitational field, diffusion only occurs

82 Fundamentals of Fluid Mechanics and Transport Phenomena

without natural convection for fluids in situations of 1D equilibrium. In other cases,

the inevitable density gradients created by variations in the component

concentrations must be taken into account: these induce complex movements due to

natural convection in the fluid.

2.4.3.3.

Diffusion in a closed container

Let us now consider a perfect, isothermal, gaseous mixture, contained in a fixed

container (Figure 2.9a), whose total volumic number of moles

n is constant. We will

suppose that the walls are impermeable; this results in a

molar average velocity

which is zero in the reference frame of the container

, which can thus be considered a

preferred reference frame:

0, with:

ii i i

nV n V V V V



¯ ¯

 

¡° ¡°

¢± ¢±



GG GGG

This results in the molar flux densities playing an important role in this reference

frame:

, with: 0

ni ni

qnV q

¯ ¯

¯



¡°

¡° ¡°

¢±

¢± ¢±



2.4.3.4

. Diffusion in steady evaporation

Let us now examine the 1D problem of steady evaporation of a liquid contained

in a vertical tube as shown in Figure 2.9b. As before, the pressure is constant in the

tube. We suppose that the temperature is constant and the composition is

independent of time, but not uniform in space. The total volumic number of moles

and the molar velocity

(section 2.4.3.2) are steady and uniform in space. The

molar flux densities of air (species 1) and vapor (species 2) are steady (section

2.4.3.2).

As the free surface of the liquid at the bottom of the tube is impermeable to air,

the flux density and velocity of the air are both zero at all points within the tube:

the

air is at rest in the reference frame of the tube

(

) and so diffusion velocity

of vapor in air can be written:

VVV

GGG



Since we have a steady evaporation regime, we can conclude that the

flux of

liquid evaporated

Vn across a cross-section of the tube is independent of the