Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.


Fluid Dynamics Equations 173
The quantity g is here the total specific energy 2
2
Ve whose balance is
obtained by writing that its variation in a domain
D is due to the external addition of
energy:
mecth
dv
V
e
dt
d
PP
D
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
³
2
2
U
[4.44]
The external additions of energy are:
– mechanical power
mec
P
provided from the exterior, which includes:
- the specific mechanical power f
i
u
i
due to the specific force f
i
in the domain
D
;
- the surface power
V
ij
n
j
u
j
due to external stresses
V
ij
n
j
on the outer surface
6of the domain
D
;
³³³³
w
w
6 DDD
P
dvu
x
dvufdsundvuf
iij
j
iiijijiimec
VUVU
– thermal power
P
th
received from the exterior, which includes:
- volume power
V
T
generated by volume source in the domain
D
;
- thermal fluxes across the outer surface 6 due to the thermal flux vector
density
T
q
G
:
dv
x
q
dvdsnqdv
j
Tj
TjTjTth
³³³³
w
w
¦ DDD
P
VV
Replacing the powers
P
th
and P
mec
in [4.44] with their values, we obtain:
³³
³³³
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
DD
DDD
PP
dv
x
u
dvuf
dv
x
q
dvdv
V
e
dt
d
j
iij
ii
j
Tj
Tmecth
V
U
VU
2
2
[4.45]
Using Ostrogradsky’s theorem to transform the surface integrals, and relation
[4.45], we get the local equation:
j
Tj
T
j
iij
ii
x
q
x
u
uf
V
e
dt
d
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
V
V
UU
2
2
[4.46]
or by introducing the viscous stress tensor [3.39]:

174 Fundamentals of Fluid Mechanics and Transport Phenomena
j
Tj
T
j
iij
i
i
ii
x
q
x
u
x
pu
uf
V
e
dt
d
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
V
W
UU
2
2
[4.47]
4.3.4.1.2.
Expression using the total enthalpy
Taking the divergent form (see [4.10]) of the left-hand side of [4.47], we have:
j
Tj
T
j
iij
ii
jj
j
x
q
x
u
uf
puu
V
e
x
V
e
t
w
w
w
w
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
V
W
U
UU
22
22
Using the definition of enthalpy (
U
peh ) then gives:
j
Tj
T
j
iij
ii
j
j
x
q
x
u
uf
u
V
h
x
V
e
t
w
w
w
w
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
V
W
U
UU
22
22
[4.48]
4.3.4.1.3.
The internal energy equation
Subtracting equation [4.26] from equation [4.46] gives:
j
Tj
T
j
i
ij
j
j
x
q
x
u
x
ue
t
e
dt
de
w
w
w
w
w
w
w
w
VV
U
U
U
[4.49]
Expanding the stress tensor, we obtain:
j
Tj
T
j
i
ij
i
i
x
q
x
u
x
u
p
dt
de
w
w
w
w
w
w
VWU
[4.50]
4.3.4.1.4.
Enthalpic and entropic forms of the energy equation
Equation [4.47] can also be written as a function the other extensive variables:
the internal energy e, the enthalpy h or the entropy s, defined by the thermodynamic
relations:
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
UU
p
ddhTdspdde
1

Fluid Dynamics Equations 175
or, taking account of relation [4.7]:
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
UU
U
U
U
p
dt
d
dt
dh
dt
ds
T
x
u
p
dt
ds
T
dt
dp
dt
ds
T
dt
d
p
dt
de
i
i
2
1
The energy equation can thus be written in one of the following forms:
j
Tj
T
j
i
ij
i
i
x
q
x
u
dt
ds
T
dt
dp
dt
dh
x
u
p
dt
de
w
w
w
w
°
°
°
¿
°
°
°
¾
½
w
w
VW
U
U
U
[4.51]
The third equation of [4.51] allows us to define the dissipation function ):
j
i
ij
x
u
w
w
)
W
[4.52]
which represents the thermal power released locally per unit volume by viscous
friction.
4.3.4.1.5.
Entropy balance
The entropic form of energy equation [4.51] is of some interest, as it in fact
constitutes an entropy balance, which is not surprising since on account of the
assumption of local equilibrium, the entropy is a state function related to the internal
energy. This equation contains the flux terms
jTj
xq ww
(divergence terms), and
volume source terms associated with
jiij
xu ww
W
and
T
V
. The entropy balance
equation can thus be written:
j
Tj
T
j
i
ij
x
q
TTx
u
Tdt
ds
w
w
w
w
1
V
W
U
[4.53]
4.3.4.1.6.
Other forms of the energy equation
The left-hand side of the energy equation can also be written using other
thermodynamic variables. For example, formula [1.27] allows us to write (
E
is
expansion coefficient [1.26] at constant volume):
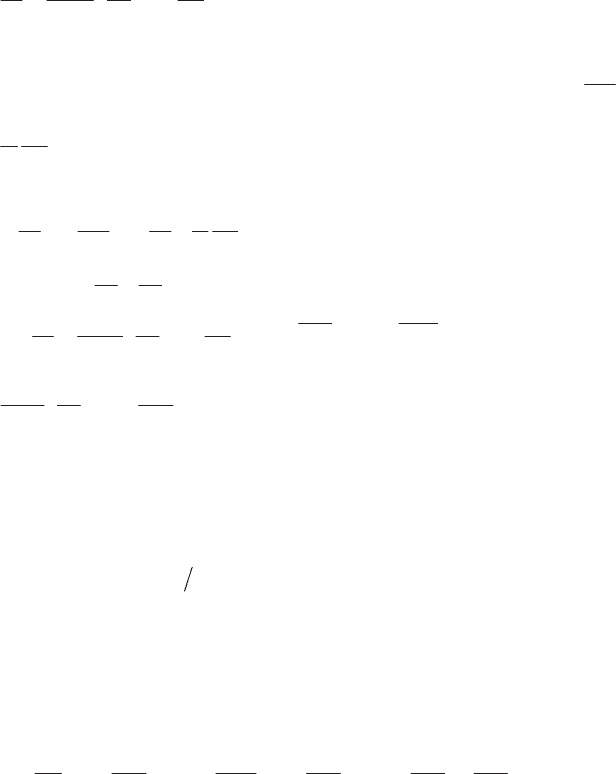
176 Fundamentals of Fluid Mechanics and Transport Phenomena
¸
¸
¹
·
¨
¨
©
§
dt
d
c
dt
dp
pT
C
dt
ds
v
U
E
2
[4.54]
Finally, equation [4.6] for the conservation of mass allows us to replace
i
i
x
u
w
w
with
dt
d
U
U
1
and to obtain other forms for the left-hand side of equation [4.51]:
j
Tj
T
j
i
ij
j
j
v
v
i
i
x
q
x
u
x
u
c
dt
dp
p
C
dt
d
c
dt
dp
p
C
dt
ds
T
dt
dp
dt
dh
dt
dp
dt
de
x
u
p
dt
de
w
w
w
w
°
°
°
°
°
¿
°
°
°
°
°
¾
½
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
VW
U
E
U
U
E
U
U
U
U
U
UU
2
2
[4.55]
The heat convection equation can be obtained from an expression of equation
[4.51] for a transformation:
at constant pressure (dp/dt = 0) using specific enthalpy h;
at constant volume (
0 ww
jj
xu
) using specific internal energy e.
For a perfect gas or an incompressible liquid, these quantities can be expressed
as a temperature function (
dTCdh
p
and dTCde
v
) and [4.51] can be written
in the following form, where, depending on the case considered, we take either C
p
or
C
v
as the specific heat C:
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
w
w
jj
T
j
i
ij
j
Tj
T
j
i
ij
x
T
xx
u
x
q
x
u
dt
dT
C
OVWVWU
4.3.4.1.7.
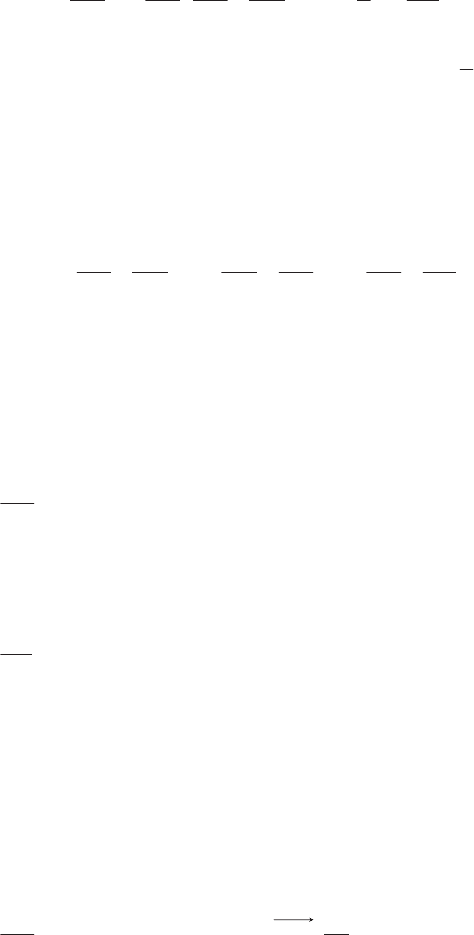
Expression of the dissipation function for a Newtonian fluid
Substituting [3.57] for the viscous tensor of a Newtonian fluid into [4.52], we
obtain ( Vdiv
G
T
):
Fluid Dynamics Equations 177
22
33
2
22
2
11
2
31
2
23
2
12
2
3
2
24
3
2
TPKHHHPHHHP
PKPW
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
w
w
)
i
i
i
j
j
i
j
i
j
i
ij
x
u
x
u
x
u
x
u
x
u
Very often, the shear velocities are much greater than the expansion velocities
and the expression for the dissipation function is simplified:
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
)
2
3
1
1
3
2
2
3
3
2
2
1
2
2
1
2
31
2
23
2
12
4
x
u
x
u
x
u
x
u
x
u
x
u
P
HHHP
[4.56]
4.3.5. Balance of chemical species
Equation [2.25] for the mass balance of a chemical species can be written using
the partial density
U
i
and the local velocity
i
V
G
of the component i:
miii
i
Vdiv
t
VU
U
w
w
G
[4.57]
The volume source of mass
V
mi
of species i is a homogenous chemical reaction.
Introducing the local mass average velocity V
G
[2.29] gives:
>@
VVdivVdiv
t
iimii
i
G
G
G
w
w
UVU
U
[4.58]
The mass flux density
VVq
iimi
G
G
U
is associated with diffusive
phenomena considered here in the reference frame of the inertia center (section
2.4.3.5). For the case of a binary mixture, this can be expressed using formula [2.69]
for non-isothermal mixtures.
In the case of isothermal diffusion, the mass flux density of the species i is given
by relation [2.57]. We thus obtain the diffusion equation of the flow:
2,1
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
igradDdivVdiv
t
i
mii
i
U
U
UVU
U
G
[4.59]

178 Fundamentals of Fluid Mechanics and Transport Phenomena
In the case where species 1 is in weak concentration, a discussion analogous to
that of section 2.4.4.2.7 leads to the following equation:
111
1
cDVcdiv
t
c
c
'
w
w
V
G
[4.60]
Recall that for a binary mixture, diffusion is represented by the balance equation
of one species, associated with the mass conservation equation for the mixture. In
simple cases, we can consider that the creation of species 1 is due to a homogenous
reaction of order
m
:
m
c
kc
11
V
[4.61]
The coefficient
k
for the reaction kinetics varies according to a law of the form:
¸
¸
¹
·
¨
¨
©
§
RT
U
kk
exp
0
The quantity
U
is the activation energy;
T
designates the absolute temperature.
The form of the preceding relation shows a strong coupling between the temperature
and the reaction speed.
4.4. Boundary conditions
4.4.1. General considerations
The partial differential equations satisfied by the preceding quantities are not
sufficient for the definition of a particular problem. We must also specify boundary
conditions of different kinds. The definition of the domain studied
D constitutes the
first step. It is defined by the surface which bounds
D and on which we will impose
conditions for the unknowns of the problem (boundary conditions). Because of the
particular nature of the time variable, we must also specify the
initial conditions
.
In fluid mechanics the boundary conditions must be carefully considered, as we
rarely encounter physical problems in entirely closed domains, since the flow must
be generated by some appropriate device (a pump, a fan, a moving vehicle, a
meteorological situation, an acoustic cavity, etc.). The domain studied is generally
limited by solid walls and zones which are connected to other zones being studied.
Fluid Dynamics Equations 179
4.4.2. Geometric boundary conditions
4.4.2.1.
Solid walls
The usual solid walls are relatively easy to treat, since the fluid touches the wall:
the velocities of the solid wall and the fluid are equal where they are in contact
. The
reason for this fact is related to the roughness of the walls on the molecular level,
and to the thermal excitation by which mean momentum is transferred from one
medium to another (it is incidentally the same as the interpretation of viscosity and
contact action). This interpretation is such that the physico-chemical nature of the
wall does not influence the adherence condition.
This adherence condition of the fluid at the wall is always very well satisfied in
ordinary conditions where the mean free path of the molecules is small compared
with the roughness. The same is not true in the study of rarefied gases, where we
must take account of the properties of the wall and introduce a slipping coefficient.
In certain cases, the walls are permeable, in other words they let some matter
pass through them. This is the case when we suck or blow through a porous
medium. In these conditions, the difference between the tangential fluid velocities
and the wall are zero at the wall. The normal fluid velocity with respect to the wall
depends on the fluid injection process. An analogous condition is encountered in the
presence of
phase changes at the wall
: evaporation, fusion, and other heterogenous
chemical reactions which consume or produce fluid.
The boundary conditions for thermal and diffusion problems were discussed in
sections 2.3.2 and 2.4.6, which the reader can refer to.
4.4.2.2.
Flow entry and exit zones
In addition to the walls which guide the flow, we generally need to specify the
conditions at the entrance or exit of the domain studied. Real flows are always
generated by machines (solid surface in movement) or by differences in conditions
between upstream and downstream reservoirs. In practice, we know how to impose
wall velocities, injection or extraction flow rates, unsteady forces on a wall (by
means of electromagnetic devices). However, it should be noted that we do not
know how to impose a given pressure or velocity distribution throughout a fluid.
In fact, the entrance of a flow into a domain is a rather particular zone, as we
have an
initial condition
which is largely analogous to that of the temporal variable
(it is in fact an initial condition in Lagrangian variables). In practice, such a zone is
found at the exit of another fluid domain and we need to specify a velocity or
pressure distribution which is compatible with the equations of motion. This is
straightforward when we can take a uniform flow or zone at rest with a constant

180 Fundamentals of Fluid Mechanics and Transport Phenomena
driving pressure in a section perpendicular to the velocity relatively far upstream of
the walls which are to guide the flow. However, in general, this is not the case, and
the choice of an incompatible velocity profile leads to difficulties (“numerical
shocks”) in the subsequent numerical solutions. The same difficulties are
encountered in thermal and acoustic studies, where initial conditions for the entropy
or other material quantities are required. We will come back to this point in section
5.6.2 when we consider the classification of partial differential equations.
Further to the preceding difficulties, we will see in Chapter 5 that certain
material properties can also be transported by waves which propagate in different
directions, including in the upstream direction. This means that the very idea of the
flow entrance (“upstream” and “downstream”) may depend on what it is we wish to
study. Remember also that the idea of an extensive quantity leads to conservation
properties which must be satisfied in the global balances, and it is not always
obvious that this condition is respected.
Finally, for flows which possess unstable zones, it is not sufficient to specify
velocity or pressure distributions: the perturbations which enter the domain must be
defined so as to fully determine the problem to be solved.
In conclusion, it is clear that we are a long way from understanding how to
proceed in all cases in order to obtain a well-posed problem.
1
4.4.2.3.
Free surfaces
The free surface of a flow
2
(or the interface between two immiscible fluids) is an
unknown boundary, on which the two following properties need to be ensured:
1) The
free surface (or the interface) is a material boundary between two
immiscible fluids
: it comprises the locus of fluid particle trajectories. Let
z
be the
altitude of this free surface
3
:
),,(
tyxz
[
The
w
component of the velocity in the O
z
direction satisfies the relation (known
as the
kinematic relation
):
1 We will here define a well-posed theoretical problem (to be solved analytically or
numerically) or an experiment whose solution is reproducible, even if we change a calculation
method or an experimental process.
2 For instance, water flows in open channels, rivers, etc.
3 The axis Oz is the opposite of the direction of external forces field, usually gravity field.

Fluid Dynamics Equations 181
y
v
x
u
tdt
d
w
w
w
w
w
w
w
[[[[
2) The physical nature of this surface must provide the conditions necessary for
the stress tensor. The pressure discontinuity
21
pp
across the surface is given by
Laplace’s law:
¸
¸
¹
·
¨
¨
©
§
'
11
21
RR
pp
V
where the quantities
V
,
R
and
R’
are, respectively, the surface tension and the radii
of curvature of the free surface at the point considered (section 2.2.1.4.2).
For nearly all industrial flows of water and aqueous solutions, surface tension
does not play an important role: we can assume pressure continuity at the free
surface.
The discontinuity of the tangential stresses is related to the physico-chemical and
flow conditions of the free surface; in particular, if the free surface contains a
surface active substance (a mono-molecular thickness layer can suffice) and is not
regenerated, it behaves like a solid surface. In many cases of water flow, the free
surface is regenerated and we have continuity of the tangential stresses between the
two media. In hydraulics, we can consider that the viscous stress is nearly equal to
zero at the free surface of a flow.
4.4.2.4.
Fully immersed flows
Fully immersed flows are flows without free surface whose upstream and
downstream conditions are hydrostatic. We have seen that in the Navier-Stokes
equations, gravity can be eliminated by using a driving pressure variable
p
g
= p +
U
gz
. This change of variables is only of interest so long as it does not result in
gravity reappearing in the boundary conditions, which should be expressed in terms
of the driving pressure and not pressure itself. This excludes flows with free surfaces
which are not horizontal (sea swells, rivers, surface runoff, etc.) for which we have,
for example, a constant pressure condition.
4.4.3. Initial conditions
No physical problem is timeless. There is always a beginning to an experiment
and therefore to its modeling. From this point of view, flow problems can be
difficult, because even if the boundary conditions are steady (independent of time),
182 Fundamentals of Fluid Mechanics and Transport Phenomena
the solution may present diverse and complex characteristics. Some examples will
demonstrate the degree of these difficulties:
– a steady solution may be established after a transition period, but this solution
may depend on the initial conditions (such properties are used in fluidics when we
manipulate the eventual hysteresis of separated flow zones);
– no steady solution may exist, but a more or less complexly established
unsteady flow regime may occur, which is determined and predictable;
– the flow may become more or less chaotic while maintaining a more or less
organized unsteadiness;
– an established turbulence may be present in certain domains of the established
flow: in other words the flow, while unsteady, may have stable statistical
characteristics;
weak perturbations, which are difficult to characterize, may be present in the
initial or boundary conditions, and these may be of considerable importance for the
evolution of the flow.
We will come back to some of these points in section 6.6.
4.5. Global form of the balance equations
4.5.1. The interest of the global form of a balance
Even the most rudimentary model must satisfy conservation laws for extensive
quantities. The interest in a global balance is that it allows us to observe a system
from the exterior. Balance equation [4.1] for a quantity
G
in the domain
D
can be
written by replacing the material derivative by its expression (section 3.3.3.3); it
can be written in one of the following two forms, as a function of the volume
quantity
g
or of the mass quantity
g
:
dsnqdvdsnugdv
t
g
jGjGii
³³³³
¦6
w
w
q
DD
V
[4.62]
dsnqdvgdqdv
t
g
jGjGm
³³³³
¦6
w
w
q
DD
V
U
[4.63]
Note that it is equivalent to writing a Eulerian balance in a domain
D which is
assumed fixed
. As we saw in section 1.1.4.2, this balance corresponds to an
open
system
.
