Попов Ю.Д., Тюптя В.І., Шевченко В.І. Методи оптимізації
Подождите немного. Документ загружается.

ax ar b i I
xr j
ij
j
n
j
s
ij
j
n
j
s
is
j
s
j
s
s
==
∑∑
+≤
+∈
11
ρ
ρ
,,
,. J
∈
J
J
Звiдки, враховуючи умови
ax b i I
xj
ij
j
n
j
s
is
j
s
s
=
∑
=∈
=∈
1
0
,,
,,
та
ρ
>0 маємо
ar i I
rj
ij
j
n
j
s
s
j
s
s
=
∑
≤∈
≥∈
1
0
0
,,
,.
(11.11)
До останньої системи додаємо умову нормування, яка обмежує довжину
вектора r
s
− 1≤ r
j
s
≤ 1, j=1,...,n. (11.12)
Серед всіх можливих напрямків знаходимо напрямок r
s
, який мінімізує
похідну по напрямку r
s
від функції f (x ) в точці x
s
. Він є оптимальним розв’язком
задачі мінімізації
,
s
),
ss
s
ffD min)((=)(
→∇ rxx
r
(11.13)
з обмеженнями (11.11) i (11.12).
Розв'язавши задачу (11.11)–(11.13), перевіряємо умову:
• якщо оптимальне значення функції (11.13) невід'ємне, то кінець обчислень,
оскільки підхожих напрямків в точці x
s
не існує; x
s
— стаціонарна точка
функції f (x ) в області D ;
• якщо оптимальне значення функції (11.13) від'ємне, то виконуємо дії пунктів 4,
5, 6, замінивши антиградієнт −∇f (x
s
) вектором знайденого можливого i
підхожого напрямку r
s
.
I pbdeZ^ 11.2. Розв'язати задачу комбінованим методом
f (x
1
,x
2
) = (x
1
− 6 )
2
+ (x
2
− 4 )
2
→ min,
x
1
+ x
2
≤ 8,
x
1
+ 3 x
2
≤ 18,
x
1
≥ 0, x
2
≥ 0,
вибираючи x
0
=(2,4).
Розв’язування. Обчислимо градієнт ∇ f (x
1
,x
2
)
∇ f (x
1
,x
2
) = (2 x
1
− 12 , 2 x
2
− 8 ).
201
1-а iтеpацiя.
∇ f (x
0
) = (− 8 , 0) ≠ 0 .
Визначаємо активні обмеження в точці x
0
:
2 + 4 = 6 < 8 ,
2 + 3 × 4 = 14 < 18 ,
2 > 0 ,
4 > 0 .
Активних обмежень немає. Точка x
0
є внутрішньою точкою допустимої області
задачі, тому напрямок антиградієнта −∇f (x
0
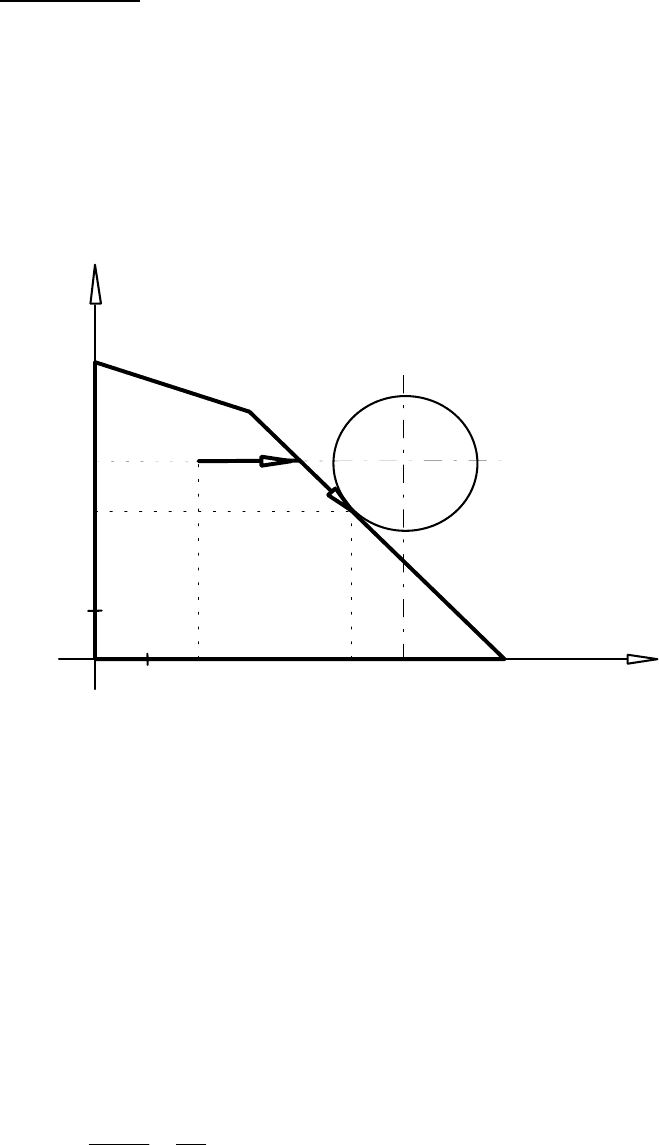
) є можливим. Будуємо
O
x
x
2
1
1
1
x *
x
0
0
r
D
.
x
1
r
1
2
4
3
6
56
8
Рис. 11.2
промінь x(
ρ
), що виходить із точки x
0
в напрямі антиградієнта −∇f (x
0
):
x(
ρ
) = x
0
−
ρ
∇ f (x
0
) = (2,4) −
ρ
(−8,0) = (2 +8
ρ
,4 ),
ρ
>0.
Визначаємо інтервал допустимих значень
ρ
:
28 48
2 8 12 18
28 0
40
0
++≤
++≤
+≥
>
>
ρ
ρ
ρ
ρ
,
,
,
,
.
Звідки маємо
ρ
∈ (0,1/4 ].
Знаходимо найменше значення функції g(
ρ
)=f (x
0
−
ρ
∇ f (x
0
))на відрізку
(0,1/4 ]. Скоpистаємось необхідними умовами екстpемуму функції однієї змінної:
dg
d
d
d
ff
()
((
ρ
ρρ
ρ
=−∇xx
00
))= ( −∇f (x
0
−
ρ
∇ f (x
0
),∇ f (x
0
))=
= −((2(2+8
ρ
)−12,0),(−8,0))=8(16
ρ
−8)=0,
звідки маємо
ρ
= 1/2 .
202

Так як
dg
d
2
2
128 0
()
ρ
ρ
=>, то
ρ
=1/2 є точкою мінімуму функції g(
ρ
) для всіх
ρ
.
Оскiльки ця точка лежить праворуч від допустимого інтервалу, а функція g(
ρ
)
опукла донизу, то мінімальне значення функції g(
ρ
) досягається на правому кінці
допустимого інтервалу для
ρ
. Отже,
ρ
0
= 1/4.
Обчислюємо x
1
= x
0
−
ρ
0
∇ f (x
0
) = (2,4) −(1/4 )(−8,0) = (4 ,4 ).
2-а iтеpацiя
.
∇ f (x
1
) = (− 4 , 0) ≠ 0 .
Визначаємо активні обмеження в точці x
1
:
4 + 4 = 8, (Активне обмеження)
4 + 3 × 4 = 16 < 18,
4 > 0,
4 > 0.
Пеpевipяємо, чи є антиградієнт −∇f (x
1
) можливим напрямком. Будуємо
промінь x(
ρ
), що виходить з точки x
1
в напрямі антиградієнта −∇f (x
1
):
x(
ρ
) = x
1
−
ρ
∇ f (x
1
) = (4,4) −
ρ
(−4,0) = (4 +4
ρ
,4 ),
ρ
>0.
Пiдставляємо точку x
1
в активне обмеження: 4 +4
ρ
+4 ≤ 8, звідки
ρ
≤ 0.
Водночас повинно бути
ρ
>0. Тому −∇f (x
1
) не є можливим напрямком.
Визначимо можливий напрямок. Hехай r
1
=(r
1
1
,r
2
1
) — вектор невідомого
можливого напрямку. Будуємо промінь x
′
(
ρ
), що виходить із точки x
1
в напрямі
r
1
:
x
′
(
ρ
) = x
1
+
ρ
r
1
= (4, 4 ) +
ρ
(r
1
1
,r
2
1
) = (4+
ρ
r
1
1
,4+
ρ
r
2
1
),
ρ
>0.
Пiдставляючи точку x
′
(
ρ
) в активне обмеження, отримаємо
4+
ρ
r
1
1
+4+
ρ
r
2
1
≤ 8,
або
r
1
1
+r
2
1
≤ 0.
Додаємо до останньої нерівності умову нормування
− 1 ≤ r
1
1
≤ 1,
− 1 ≤ r
2
1
≤ 1.
Знаходимо похідну за напрямком r
1
від функції f(x ) в точці x
1
:
D
r
1
f (x
1
)= (∇ f (x
1
), r
1
) = ((
−
4, 0), (r
1
1
,r
2
1
)) =
−
4 r
1
1
.
Остаточно отримуємо задачу ЛП для визначення підхожого i можливого
напрямку
− 4 r
1
1
→ min,
r
1
1
+r
2
1
≤ 0,
− 1 ≤ r
1
1
≤ 1,
− 1 ≤ r
2
1
≤ 1.
Оптимальним pозв'язком цієї задачі є вектор r
1
=(1,-1). Відповідні значення
r
1
1
, r
2
1
дорівнюють r
1
1
=1, r
2
1
=−1. Значення похідної за напрямком r
1
D
r
1
f (x
1
)=
−
4 r
1
1
=
−
4< 0.
203

Отже, напрямок r
1
=(1,−1) є можливим i підхожим. Будуємо промінь x
′
(
ρ
), що
виходить із точки x
1
в напрямку r
1
:
x
′
(
ρ
) = x
1
+
ρ
r
1
= (4, 4 ) +
ρ
(1,−1) = (4+
ρ
,4−
ρ
),
ρ
>0.
Пiдставляючи x
′
(
ρ
) у неактивні обмеження, визначаємо допустимий інтервал
для
ρ
:
434 1
40
40
0
++ − ≤
+≥
−≥
>
ρρ
ρ
ρ
ρ
(),
,
,
.
8
Розв'язуючи систему, отримаємо 0 <
ρ
≤ 4.
Обчислимо найменше значення функції g(
ρ
)=f (x
1
+
ρ
r
1
) на відрізку (0,4 ].
Маємо
dg
d
d
d
f
()
(
ρ
ρρ
ρ
=+
x
1
r)
1
= ( ∇ f (x
1
+
ρ
r
1
),r
1
)=
= ((2(4+
ρ
)−12 ,2(4−
ρ
)−8) , (1,−1))=4
ρ
−4=0,
звідки знаходимо
ρ
=1.
Так як
dg
d
2
2
40
()
ρ
ρ
=>, то
ρ
=1 є точкою мінімуму опуклої донизу функції g(
ρ
).
Точка
ρ
=1 належить допустимому інтервалу для
ρ
. Тому
ρ
1
=1 i
x
2
= x
1
+
ρ
1
r
1
= (4, 4 ) + (1,−1) = (5,3).
3-я iтеpацiя
. Обчислюємо
∇ f (x
2
) = (− 2 , − 2 ) ≠ 0 .
Визначаємо активні обмеження в точці x
2
:
5 + 3 = 8, (Активне обмеження)
5 + 3 × 3 = 14 < 18,
5 > 0,
3 > 0.
Пеpевipяємо, чи буде антиградієнт −∇f (x
2
) можливим напрямком. Будуємо
промінь, що виходить з точки x
2
в напрямі антиградієнта −∇f (x
2
):
x(
ρ
) = x
2
−
ρ
∇ f (x
2
) = (5,3) −
ρ
(−2,−2 ) = (5 +2
ρ
,3+2
ρ
),
ρ
>0.
Пiдставляємо точку x(
ρ
) в активне обмеження: 5 +2
ρ
+3+2
ρ
≤8, звідки
ρ
≤ 0.
В той же час
ρ
>0. Тому −∇f (x
2
) не є можливим напрямком.
Будуємо допоміжну ЗЛП для відшукання можливого напрямку. Hехай
r
2
=(r
1
2
,r
2
2
) — вектор невідомого можливого напрямку, x
′
(
ρ
) — промінь у
напрямку r
2
. Маємо
x
′
(
ρ
) = x
2
+
ρ
r
2
= (5,3) +
ρ
(r
1
2
,r
2
2
) = (5+
ρ
r
1
2
,3+
ρ
r
2
2
),
ρ
>0.
Пiдстановка x
′
(
ρ
) в активне обмеження дає нам
5+
ρ
r
1
2
+3+
ρ
r
2
2
≤ 8 ,
ρ
>0,
або з умовами нормування
204

r
1
2
+r
2
2
≤ 0,
− 1 ≤ r
1
2
≤ 1,
− 1 ≤ r
2
2
≤ 1.
За цих умов ми повинні мiнiмiзувати функцію
D
r
2
f (x
2
)= (∇ f (x
2
), r
2
) = ((−2,
−
2), (r
1
2
,r
2
2
)) =
−
2 r
1
2
−
2 r
2
2
.
Оскiльки r
1
2
+r
2
2
≤ 0, то −2 (r
1
2
+r
2
2
)≥ 0, тобто підхожих напрямків не існує. Отже,
точка x *=x
2
=(5 ,3 ) є оптимальним pозв'язком задачі, f (x *)=f(5,3)=2.
§ 3. F_l h^ ijh_dp ]jZ^}gl Z
Розглянемо задачу пошуку умовного екстремуму, яка полягає в мінімізації
цільової функції z=f
0
(x ), x ∈ E
n
, f (x )∈ C
1
, за умови, що x ∈ D, де D — опукла
множина, зокрема,
D = {x ∈ E
n
: f
i
(x )≤0, f
i
(x ) — опуклі функції, i=1,...,m, x ≥ 0 }.
Як вже зазначалось, в градієнтних методах у разі виходу точки x
s
на границю
допустимої множини напрямок антиградієнта перестає бути, взагалі кажучи,
можливим. У цьому випадку замість процедури
x
s+
1
=x
s
−
ρ
s
∇ f
0
(x
s
), s =1,2,..., (11.14)
повинна бути розглянута інша процедура, яка дозволяє перейти від допустимої
точки x
s
до іншої допустимої точки x
s+
1
таким чином, щоб значення цільової
функції f
0
(x ) зменшилось. Іншими словами, у співвідношенні (11.14) необхідно
замість неможливого напрямку −∇f
0
(x
s
) розглянути деякий можливий напрямок
r
s
. Для знаходження цього напрямку розглянемо точку x
s
−
ρ
∇ f
0
(x
s
) (
ρ
>0) та
спроектуємо її на область D. Одержимо точку y
s
=
π
D
(x
s
−
ρ
∇ f
0
(x
s
)), де
π
D
—
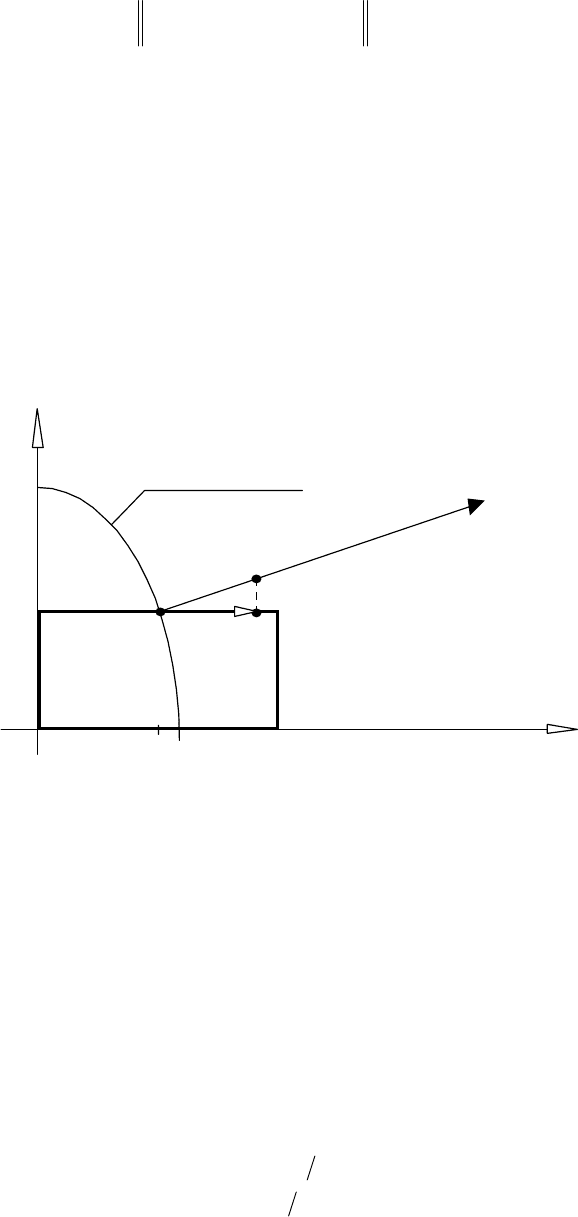
оператор проектування на область D. Оскільки множина D — опукла, то відрізок
[x
s
,y
s
] ∈ D, а, отже, напрямок r
s
=y
s
–x
s
— можливий (див. рис. 11.3).
D
Z
2
Z
1
z
s
x
s
r
s
y
s
−∇
f
(
x
s
)
x
s
−ρ
∇
f
(
x
s
)
z
1
<
z
2
<…<
z
s
Рис. 11.3
Тепер замість процедури (11.14) в методі проекції градієнта розглянемо
процедуру
x
s+
1
=x
s
−
ρ
s
r
s
, s =1,2,..., (11.15)
де
ρ
s
>0 обирається так, щоб f
0
(x
s+
1
)<f
0
(x
s
) та x
s+
1
∈ D.
205
У випадку довільної опуклої області D задача пошуку проекції y
s
надто
складна. З аналітичної точки зору, як вже відзначалось (див. Розділ 6, §4), вона
полягає у знаходженні точки y
s
∈D, найближчої до даної точки x
s
−
ρ
∇ f
0
(x
s
)∉ D:
.
2
s0ss
f yxxy
Dy
−∇=
−
∈
))((minarg
ñ (11.16)
У задачі (11.16) цільова функція — квадратична та опукла донизу. Отже, якщо
допустима множина D задається лінійними обмеженнями, то ця задача є задачею
опуклого квадратичного програмування, яка може бути розв'язана квадратичним
симплекс-методом.
I pbdeZ^ 11.3. Розв'язати методом проекції градієнта задачу
z=f
0
(x
1
,x
2
)=− x
1
4
−x
2
→min,
0 ≤ x
1
≤ 2,
0 ≤ x
2
≤ 1.
Проведемо одну ітерацію методу, вибираючи x
s
= (1,1) (див. рис. 11.4).
O
1
1
x *
D
x
s
−ρ∇
f
(
x
s
)
−∇
f
(
x
s
)
x
1
x
2
y
s
r
s
−
x
1
4
−
x
2
=
−
2
Рис. 11.4
Маємо
f
0
(x
s
)=2, ∇ f
0
(x
1
,x
2
)=(−4x
1
3
,−1), ∇ f
0
(x
s
)=(−4,−1),
x
s
−
ρ
∇ f
0
(x
s
)= (1+4
ρ
,1+
ρ
).
Ясно, що x
s
−
ρ
∇ f
0
(x
s
)∉ D при будь-якому
ρ
>0, і тому напрямок −∇ f
0
(x
s
) —
неможливий. Для знаходження проекції y
s
точки x
s
−
ρ
∇ f
0
(x
s
) на множину D
необхідно розв'язати таку задачу опуклого квадратичного програмування:
(1+4
ρ
–y
1
)
2
+(1+
ρ
–y
2
)
2
→ min,
0 ≤ y
1
≤ 2,
0 ≤ y
2
≤ 1.
Розв'язком вказаної задачі є вектор
y
s
=
+<
>
( )
( )
14 1 0 14
21 14
ρρ
ρ
,,
,, ,
≤,
206
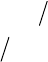
звідки маємо
ryx
sss
=−=
<≤
>
( )
( )
400 14
10 14
ρρ
ρ
,,
,, .
,
m01
Зрозуміло, що обидва варіанти останнього співвідношення задають один і той
же напрямок. За цей напрямок можна обрати вектор r
s
=(1,0 ). Після обчислення
величини можливого, а потім і оптимального, кроку у заданому напрямку
(
ρ
s+1
=1 ) отримуємо: x
s+
1
= (2,1) і при цьому f
0
(x
s+
1
)=−9 . Можна впевнитись,
що знайдений розв'язок — оптимальний. Отже, остаточно маємо: x
*
= (2,1),
f
0
(x
*
)=−9 .
Зауважимо, що у випадку, коли f
0
(x )∉ C
1
, але f
0
(x ) — опукла функція,
заміна градієнта ∇ f
0
(x
s
) на субградієнт f
0
(x
s
) у процедурах, що описані вище,
дає метод проекції субградієнта. Цікаво, що при цьому вихідна задача є задачею
опуклого програмування, і тому її розв'язок забезпечує глобальний мінімум
цільової функції.
$
∇
Jha^e 12. F_lh^b rljZngbo lZ [Zj '}jgbo nmgdpc
Iдея методів штрафних та бар'єрних функцій полягає в зведенні ЗНЛП з
обмеженнями до спеціальної задачі безумовної оптимізації. При цьому обмеження
вихідної задачі включаються в цільову функцію цієї допоміжної оптимiзацiйної
задачі. Зауважимо, що ця ідея вже використовувалась при розв'язуванні класичної
задачі пошуку умовного екстремуму методом Лагранжа, а також в задачі опуклого
програмування (теорема Куна-Таккера).
Нехай маємо задачу
min {f
0
(x ): f
i
(x )≤ 0 , i=1,...,m, x ∈ E
n
}. (12.1)
Введемо до розгляду функцію
P
DEf i
D
ni
()
{ ( ) , = ,..., },
x
xx x
x
=
∈= ∈ ≤
∞∉
0,:
,.
(12.2)
Замiнимо задачу умовної оптимізації (12.1) задачею безумовної оптимізації
min {F (x ): F (x ) = f
0
(x ) + P (x ), x ∈ E
n
}. (12.3)
Функцiю P (x ) називають штрафною, оскільки вона викликає нескінченний
штраф за вихід з області D.
Очевидно, що оптимальні розв'язки задач (12.1) i (12.3) однакові.
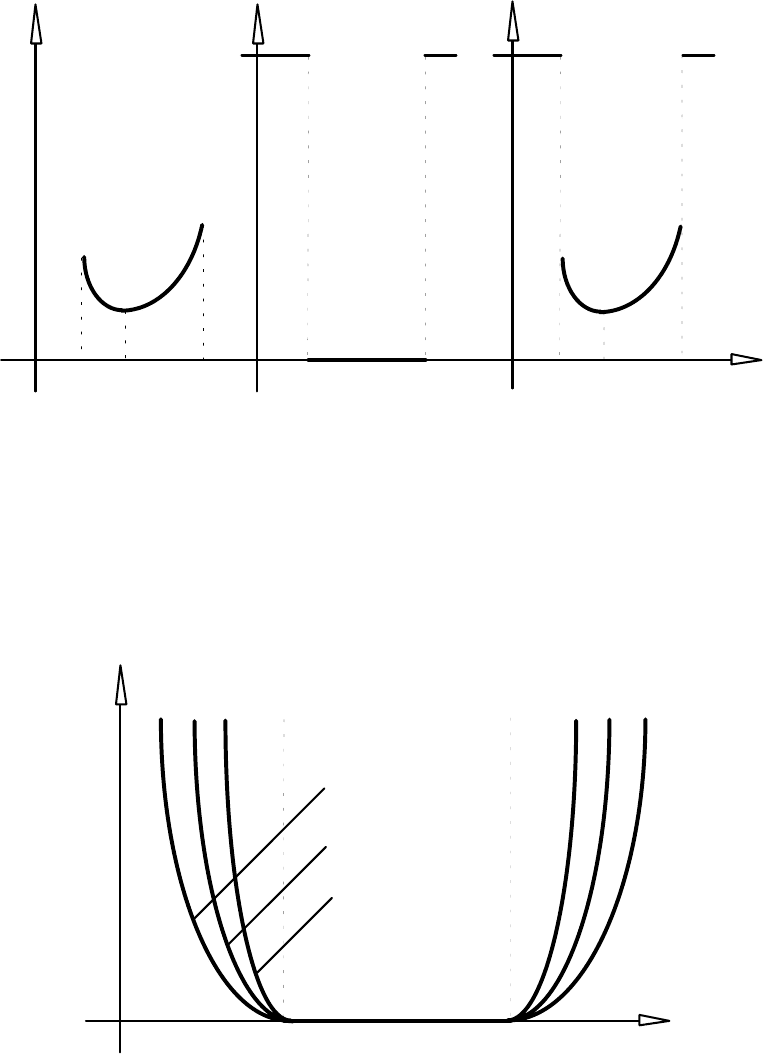
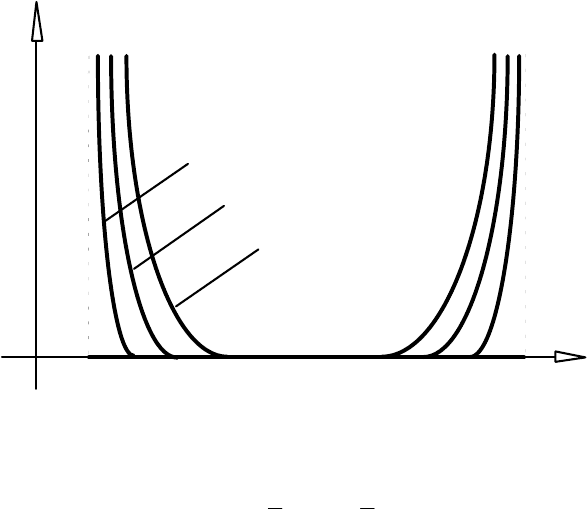
Геометрична інтерпретація викладеного для функції однієї змінної приведена
нижче (див. рис. 12.1).
Очевидно також i те, що для так введеної функції штрафу P(x ) (див.
співвідношення (12.2)) задача (12.3) розв'язуванню не піддається. Тому в дійсності
замість вказаної P(x ) розглядається послідовність штрафних функцій, які
апроксимують P(x ) i мають хороші аналітичні властивості.
HagZq_ggy 12.1. Функцiя P(f
1
(x ),...,f
m
(x ),r ), де r =(r
1
,...,r
m
) — деякий
вектор керуючих параметрів, а f
i
(x ), i=1,...,m, — функції обмежень задачі (12.1),
називається штрафною, якщо
207
lim ( ,..., , )
, = ,..., ,
()rim
m
i
i
Py y
yi m
віншому
→∞ =
=
≤
∞
1
1
001
,...,
,
,.
r
випадку
O
x
f x( )
P x( )
F x( )
O
O
x*
x*
oooo
Рис. 12.1
Замiсть задачі (12.3) введемо до розгляду послідовність задач безумовної
оптимізації
min {F (x,r) = f
0
(x ) + P (f
1
(x ),...,f
m
(x ),r )}. (12.4)
Метод штрафних функцій полягає в переході від задачі (12 .1) до
послідовності задач безумовної оптимізації (12 .4) з наступним їх розв'язуванням
яким-небудь методом безумовної оптимізації.
O
x
P x
( )
r
D
P
P
P
3
2
1
Рис. 12.2
При вдалому виборі штрафних функцій P(f
1
(x ),...,f
m
(x ),r ) можна
очікувати, що послідовність розв'язкiв задач (12.4) буде збігатися до розв'язку
задачі (12.1).
Вкажемо на відмінність методу бар'єрних функцій від методу штрафних
функцій. В методі штрафних функцій апроксимацiя функції P(x) здійснюється зовні
208
області D (див. рис. 12.2), а в методі бар'єрних функцій функції
B (f
1
(x ),...,f
m
(x ),r ) наближають P(x) зсередини області D (див. рис. 12.3).
O
x
B x
( )
r
D
B
1
B
B
2
3
Рис. 12.3
Найчастiше за штрафну вибирають функцію такого вигляду
,fP
r
1
P
r
1
rffP
m
1i
i
i
m1
∑
=
))( (=)(=)),(),...,( (
xxxx
(12.5)
де r — керуючий параметр, а функції P
i
(y ) визначені, неперервні i невід'ємні для
довільного y, причому: P
i
(y )=0 при y ≤0 і P
i
(y )→∞ монотонно при y →∞.
Прикладами функцій P
i
(f
i
(x )) можуть бути такі функції:
P
i
1
(f
i
(x )) = max {0, f
i
(x )}, (12.6)
P
i
2
(f
i
(x )) = [max {0, f
i
(x )}]
2
. (12.7)
Зауважимо, що функція (12.6) в загальному випадку недиференцiйовна,
навіть, якщо f
i
(x )∈ C
1
, в той час як функція (12.7) — диференцiйовна, якщо
диференцiйовна f
i
(x ).
Якщо ж обмеження задачі (12.1) мають вигляд рівнянь f
i
(x )=0 , i=1,...,m, то
функції P
i
(y ) у (12.5) повинні задовольняти такі умови: P
i
(y )=0 при y =0 і
P
i
(y )→∞ монотонно при y →∞. Для цього випадку функції P
i
(f
i
(x ))
найдоцільніше вибирати у вигляді
P
i
(f
i
(x )) = [f
i
(x )]
2
.
L_hj_fZ 12.1 (ijh a[‘gkl v f_l h^m rl jZn gbo nmgdp c ). Нехай x * є
розв'язком задачі (12.1)
),(minarg
xx
x
0
D
f*
∈
=
(12.8)
а x * (r ) ∀r>0 є розв'язком задачі (12.4)
209

).(minarg)( r,Fr*
n
E
xx
x
∈
= (12.9)
Якщо штрафна функція визначається рівністю (12.5), функції f
i
(x ),
i=1,...,m, неперервні i існує замкнена множина Y⊂ E
n
така, що x * (r )∈ Y ∀ r >0 ,
то
.*fr,rF
0
0r
)())(*(lim xx =
→
(12.10)
Доведення. Доведемо, що одночасно мають місце дві нерівності
.*fr,rF
0
0r
)())(*(lim xx ≤
→
(12.11)
.*fr,rF
0
0r
)())(*(lim xx ≥
→
(12.12)
Це i буде означати, що виконується рівність (12.10).
Доведемо нерівність (12.11). Маємо ∀r
2
> 0 в силу (12.9)
.r,rFr,Fr,rF
121
E
11
n
))(*()(min))(*( xxx
x
≤=
∈
(12.13)
Нехай r
1
≥ r
2
> 0. Оскiльки за означенням (12.5) P (x )≥0, то
(1
/
r
1
) P (x * (r
2
)) ≤ (1
/
r
2
) P (x * (r
2
)).
Тоді
F (x * (r
1
), r
1
) ≤ F (x * (r
2
), r
1
) = f
0
(x * (r
2
)) + (1
/
r
1
) P (x * (r
2
)) ≤
≤ f
0
(x * (r
2
)) + (1
/
r
2
) P (x * (r
2
)) = F (x * (r
2
), r
2
).
Отже при r
1
≥ r
2
> 0
F (x * (r
1
), r
1
) ≤ F (x * (r
2
), r
2
), (12.14)
тобто при спаданні r функція F (x * (r ), r ) не спадає.
За означенням (12.5) P (x )=0 при x ∈ D. Тому P (x * )=0, оскільки x * ∈ D, i
.fP1/rfr,Fr,Fr,rF
00
E
n
*)(*)()(*)()*()(min))(*( xxxxxx
x
=+=≤=
∈
(12.13)
Отже, ∀r > 0
F (x * (r ), r ) ≤ f
0
(x * ). (12.15)
Тоді існує границя
*Fr,rF
0r
=
→
))(*(lim x (12.16)
i виконується нерівність
.*)())(*(lim xx
0
0r
fr,rF*F ≤=
→
(12.17)
Доведемо тепер нерівність (12.12). Маємо ∀r
1
> 0
.r,rFr,Fr,rF
212
E
22
n
))(*()(min))(*( xxx
x
≤=
∈
(12.18)
210
