Qiu X.G. (Ed.) High Temperature Superconductors

Подождите немного. Документ загружается.

342 High-temperature superconductors

43X

barrier thickness too much. The use of noble elements Au und Ag for non-epitaxial

types of junctions is possible but the problems with the control of the interfaces

(e.g. growth and interface resistance) are a handicap to these junctions.

Very promising results were obtained for ‘native’ or ‘natural’ barriers where

etched surfaces of high-T

superconductors are used as interface-engineered barriers.

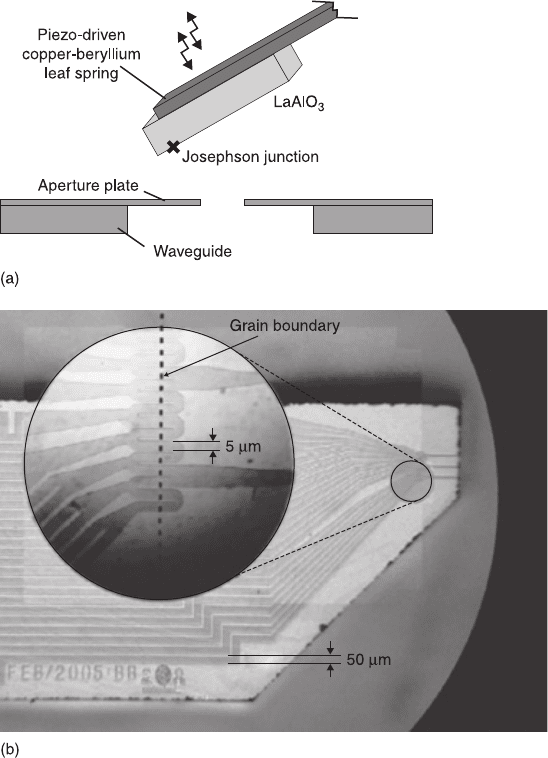
8.21 (a) Schematic drawing of the setup used for microwave scanning

microscopy and (b) layout of the Josephson cantilever (Schilling

et al., 2006, Figs 1 and 2, Copyright (2006) by the American Institute of

Physics). Reprinted with permission from Schilling M, Kaestner A, and

Stewing F (2006), ‘Room temperature near ﬁeld microwave imaging

with an YBa

Josephson cantilever’, Appl. Phys. Lett. 88, 252507,

Figs 1 and 2, Copyright (2006) by the American Institute of Physics.



High-T

Josephson junctions 343

43X

These thin parts of the superconductor show modiﬁed properties and act as normal or

semiconducting barriers. An impressive TEM picture of such a ramp-edge junction

with a ‘native’ barrier of about 2 nm thickness from Wen et al. (2000) is shown in

Fig. 8.22. For an excellent review of TEM on ramp-edges with different materials

including ‘interface engineered’ barriers see Merkle et al. (1999). The nature of the

barrier material determines the transport mechanism. Tunnelling through insulators

requires very thin layers which can be hardly realized in planar SIS junctions with

insulating barriers. Up to now there exist only a few groups successfully working

with such planar SIS junctions and it is not clear if additional current contributions

like tunnelling via traps or hopping processes dominate the simple tunnelling

mechanism. Kito et al. (2002) therefore introduced an additional PrGaO

layer and

got excess-current free junctions with I

products of about 2 mV at 4.2 K. For

semiconducting (Sm) barrier materials the thickness can be enhanced, but the

problem with additional current contributions is enhanced too. Also the effect of

induced superconductivity (proximity effect) has to be taken into account.

For some materials even an anomalous or ‘gigant proximity effect’ was

reported, e.g. Golubov and Kuriyanov (1998), leading to barrier thicknesses of up

to 200 nm. This gave a good chance to use the simple trench geometry of Sm-S

bilayers (Fig. 8.9b) but problems with interface resistance as well as with

microshorts across the trench appeared (Barholz et al., 2000). The trench geometry

8.22 TEM picture of a ramp-edge junction with a ‘native’ barrier

(thickness about 2 nm) indicated by dashed lines, so-called interface-

engineered junction. The crystallographic c-axis direction of the YBCO

ﬁlms is given by arrows (Wen et al., 2000, Fig. 2, Copyright (2000) by

Elsevier Science Ltd). Reprinted with permission from Wen JG, Satoh

T, Hidaka M, Tahara S, Koshizuka N, and Tanaka S (2000), ‘TEM study

on the microstructure of the modiﬁed interface junction’, Physica C 337,

249–255, Fig. 2, Copyright (2000) by Elsevier Science Ltd.



344 High-temperature superconductors

43X

with a N-S bilayer also was used for MgB

epitaxially grown on normal conducting

TiB

ﬁlms on SiC substrate by Chen et al. (2006). A trench smaller than 50 nm

was realized by e-beam lithography and ion milling or by focussed ion beam. The

junctions show RSJ-like IV-characteristics up to 31 K.

The use of normal conducting barriers gives the chance to enhance the barrier

thickness again but leads to other transport mechanisms as proximity effect and

multiple Andreev reﬂections have to taken into account. Additional problems

appear because materials usable for epitaxy often show magnetic ordering effects

leading to strong inﬂuences on superconductivity and Josephson effects.

The directly written junctions or modiﬁed bridges use barrier material which is

produced by electron or ion beams, thus many aspects of technology can use these

materials and their properties. The changes in the material by electron beams

mostly are not stable at room temperature but this can be improved by a thermal

annealing step. An excellent review on these FEBI junctions was given by

Pauza et al. (1997) and the proximity effect coupling was described by Booij

et al. (1997). On the other side, the ion beam modiﬁed materials are stable but

were dominated by complex behaviour, e.g. bridges work as Josephson

junctions only in a very limited temperature range, see e.g. Schmidl et al. (1997),

Katz et al. (2000), and the short review of Tinchev (2007) including the references

therein.

8.4.2 Preparation and performance of artiﬁcial barrier

junctions

Most of the problems in preparation of artiﬁcial barrier junctions are based on

their physical problems given above. The heteroepitaxy problem is mainly solved

for selected material combinations. Two examples are shown in Fig. 8.23, for

details see the review of Merkle et al. (1999). Molecular beam epitaxy (MBE),

laser MBE and pulsed laser deposition (PLD) show excellent results for multilayer

systems with crystallographically ﬁtting materials. The metal electrodes (mainly

Au) are included in devices as well as passivation and protection layers.

The simple technology for modiﬁed microbridge junctions seems to be of

interest for many junction circuits where the junction can be placed everywhere

on the substrate, but their quite low reproducibility, large parameter spread and

stability problems up to now have limited applications. The junction behaviour is

strongly dependent on the barrier properties and the transport and coupling

mechanisms. Instead of clear Josephson coupling these additional effects lead to

differences in the IV-characteristics (often ﬂux-ﬂow like but RSJ-like at lower

temperatures, Fig. 8.24), the microwave response, the temperature dependence of

the junction parameters or additional noise. Focused electron-beam irradiated

junctions with I

products of about 2 mV at 4.2 K, 650 µV at 40 K, and 120 µV

at 77 K have been demonstrated by Pauza et al. (1997). Ion beam modiﬁed

microbridges reach 200 µV at 45 K but have a spread in critical currents of up to



High-T

Josephson junctions 345

43X

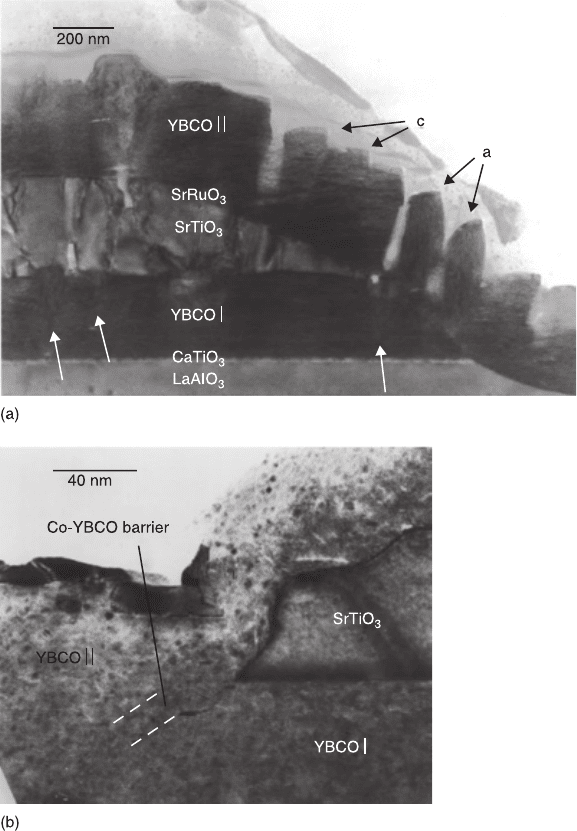
8.23 TEM pictures of artiﬁcal barrier junctions: (a) YBCO/SrRuO

YBCO ramp-edge, (b) Co-YBCO barrier SNS ramp-edge. In (a) some

a- and c-oriented grains are marked by arrows (Merkle et al., 1999, Figs

9 and 16b, Copyright (1999) by Elsevier Science Ltd). Reprinted with

permission from Merkle KL, Huang Y, Rozeveld S, Char K, and Moeckly

BH (1999), ‘Electron microscopy of high-T

Josephson junctions formed

in the epitaxial layer ramp-edge geometry: YBCO/barrier/YBCO’,

Micron 30, 539–559, Figs 9 and 16b, Copyright (1999) by Elsevier

Science Ltd.



346 High-temperature superconductors

43X

40% (Katz et al., 2000). Further improvement of the I

product was obtained

by Sirena et al. (2007) by increasing the ion energy.

It should be mentioned that ion beam modiﬁed junctions have been realized too

for MgB

superconductors by Cybart et al. (2006). Twenty-junction arrays and

single junctions with an I

product of 75 µV at 37.2 K have been demonstrated.

In contrast to low-T

devices the artiﬁcial barrier layer type is not the

standard junction technology for HTS. The interface-engineered barriers will be

a way out towards applications, because I

products over 5 mV at 4.2 K with a

good uniformity in I

for more than 100 junctions were obtained by Shimakage

et al. (2001).

8.4.3 Selected applications of artiﬁcial barrier junctions

The recent progress in single ﬂux quantum (SFQ) device technology in Japan is

based mainly on the development of interface-engineered ramp-edge junctions

(Tanabe and Hidaka, 2007). The spread in the critical current for one hundred

junctions is smaller than 10% (Satoh et al., 2001) while the I

product is larger

than 1 mV at 40 K (Morimoto et al., 2006). SFQ circuits with up to 200 Josephson

junctions were realized. A variety of elementary SFQ circuits such as a toggle

ﬂip-ﬂop, switches and an analog-to-digital converter have been designed for

operation temperatures of 30 to 50 K, while a prototype on-chip sampler system

is being developed by Maruyama et al. (2007) for demonstration of bandwidth

over 100 GHz for optical input signals, Fig. 8.25.

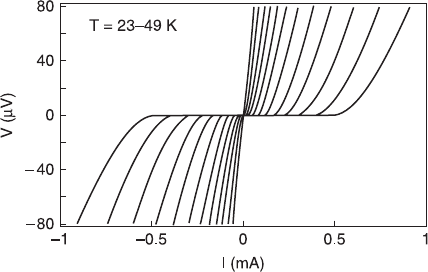
8.24 IV-characteristics of ion beam modiﬁed microbridges (ﬁlm

thickness 50 nm, slit width 250 nm) showing in general a ﬂux-ﬂow

behaviour depending on preparation and working temperature. Only

at lower temperatures is there an RSJ-like behaviour (Schmidl et al.,

1997, Fig. 7, Copyright (1997) by Springer Science and Business Media).

Reprinted with permission from Schmidl F, Dörrer L, Wunderlich S,

Machalett F, Hübner U, et al. (1997), ‘Superconducting properties of ion

beam modiﬁed YBCO microbridges’, J. Low Temp. Phys. 106, 405–416,

Fig. 7, Copyright (1997) by Springer Science and Business Media.



High-T

Josephson junctions 347

43X

As one example for application of ion beam modiﬁed junctions, the

superconducting quantum interference ﬁlters (SQIFs) of Cybart et al. (2008)

should be mentioned, even if they could be included in the SQUID chapter, too.

The SQIFs are SQUID-like arrays with a special variation of loop size leading to

8.25 SFQ sampler system using interface-engineered ramp-edge

junctions: (a) block diagram and microphotograph of the on-chip

sampler for pulse measurement. The inset shows an enlargement of the

circuit. (b) Measured current pulse (Maruyama et al., 2007, Figs 2 and

5, Copyright (2007) by Elsevier Science Ltd). Reprinted with permission

from Maruyama M, Wakana H, Hato T, Suzuki H, Tanabe K, et al. (2007),

‘Observation of SFQ pulse using HTS sampler’, Physica C 463–465,

1101–1105, Figs 2 and 5, Copyright (2007) by Elsevier Science Ltd.



348 High-temperature superconductors

43X

one single peak in their voltage-ﬂux dependence with very large transfer

coefﬁcients

∂

B (see e.g. Schultze et al., 2003 and references therein). Series

arrays of 280 such incommensurate SQUIDs from YBCO ion damage Josephson

junctions show a spread of critical currents of 12% only and result in a maximum

transfer function of 105 V/T.

8.5 Intrinsic Josephson junctions

8.5.1 Physics of intrinsic Josephson junctions

Since the discovery of the intrinsic Josephson effects by Kleiner et al. (1992) a lot

of works have been published concerning the physics of the intrinsic junctions,

e.g. Kleiner and Müller (1994), Kim et al. (1999), Yurgens (2000), Wang et al.

(2001a, 2001b, 2005, 2009), Tachiki et al. (2005, 2009), Gray et al. (2009). Thus

we will restrict ourself here to facts which are relevant for application.

The crystal structure of the high-T

superconducting cuprates offers a natural

way to realize Josephson junctions on an atomic scale. The superconducting CuO

planes are separated by coupling layers of some tenth of a nanometer. This leads to

many differences compared to artiﬁcially prepared planar barrier junctions with

quite compact superconducting electrodes and much thicker single barrier layers.

For example the magnetic ﬁeld dependence of the critical Josephson current is still

a Fraunhofer-like dependence, eq. [8.2], but relating to the atomic size of the

junction (total junction thickness is about 1.5 nm) a ﬂux quantum requires new

ﬁelds in the Tesla range. This is an advantage for some applications where stable

Josephson currents even in higher ﬁelds are necessary. The other main difference

to artiﬁcial junctions is that intrinsic junctions are naturally series arrays instead of

single junctions. Thus the observed IV-characteristic is a sum of single junction

characteristics leading to many branches up to high voltages, Fig. 8.26. For very

high voltages the heat dissipation leads to non-equilibrium effects and negative

differential resistance parts in the IV. While the number of junctions in the intrinsic

arrays is quite easy to control by thickness of the stack of superconducting unit

cells their homogeneity is still a problem. Thus there is a quite large spread in

single junction parameters. If the spread can be reduced, the internal synchronization

of the junctions improves the dynamic of these arrays. Additional shunting or

resonance environment can further improve the synchronization leading to a

collective many-junction behaviour (Grib and Seidel, 2009; Grib et al., 2002;

Seidel et al., 2001; Wang et al., 2000). This is of relevance, for example, for

radiation sources realized by intrinsic arrays. The lateral dimensions of intrinsic

Josephson junctions play a crucial role, too. Perpendicular to the atomic arrays

there is ﬂux-ﬂow of Josephson vortices corresponding to these dimensions. This

results in plasma waves and additional dynamic effects; for details see the reviews

of Saval’ev et al. (2010) and Hu and Lin (2010). On the one hand, such effects can

be applied for radiation sources (Gray et al., 2009; Tachiki et al., 2005), while on



High-T

Josephson junctions 349

43X

the other hand they lead to a complex behaviour and additional noise contributions,

see e.g. Wang et al. (2009), Tachiki et al. (2009) and references therein.

8.5.2 Preparation and performance of intrinsic Josephson

junctions

While the ﬁrst investigations on the intrinsic junctions used single crystals like

whiskers or etched parts out of them, different thin ﬁlm technologies have since been

developed. Thin ﬁlm structures used a mesa-type geometry whereas the high-T

ﬁlm

is patterned with lateral dimensions in the µm range, e.g. Schmidl et al. (1995),

Haruta et al. (2009) and references therein. The problem of metal electrodes to the

mesas was solved by Seidel et al. (1996) even for a four-point-measurement which

requires two separated contacts on top of each mesa, see Fig. 8.27. A very interesting

technology of preparation of quite homogeneous and well-deﬁned junction arrays

was proposed by Kim et al. (1999) for single crystal whiskers and later adapted by

Wang et al. (2001b) to single crystal pieces mounted on substrates. Focussed ion

beams were used to etch the small well-deﬁned stack of junctions out of the material

from two sides in a way that the remaining high-T

materials act as electrodes to the

stack. By this ‘double-sided fabrication method “or” ﬂip-chip technique’ the quality

and homogeneity of the intrinsic junction arrays was dramatically improved.

Other technologies were developed to realize a very small junction number

down to the single junction limit, see e.g. Yurgens (2000), You et al. (2006), and

Yurgens et al. (2008). Koval and co-workers (2010) showed that T

, I

and R

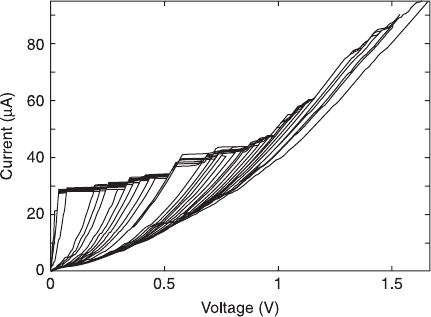
8.26 Typical IV-characteristics of an intrinsic Josepshon junction array

(1995) by IOP Publishing Ltd). Reprinted with permission from

Schmidl F, Pfuch A, Schneidewind H, Heinz E, Dörrer L, et al. (1995),

‘Preparation and ﬁrst measurements of TBCCO thin ﬁlm intrinsic

stacked Josephson junctions’, Supercond. Sci. Technol. 8, 740–743,



350 High-temperature superconductors

43X

intrinsic Bi-2212 Josephson junctions can be tuned in a large range by current

injection. This carrier injection effect is reversible and persistent.

An alternative way to realize a thin ﬁlm intrinsic stacked junction array uses

substrates with a surface not parallel to the CuO

-planes (Chana et al., 2000). On

such vicinal cut substrates the ﬁlm grows with CuO

-planes tilted with respect to

the surface (Fig. 8.14c). Patterning of a microbridge results in a nearly horizontal

stack of junctions and the length of the microbridge corresponds to the number of

junctions in series. Intrinsic Josephson behaviour of the microbridges was observed

for misorientation angles equal or larger than 15 degrees (Mans et al., 2006). This

kind of array offers new possibilities for synchronization (Grib et al., 2006).

8.5.3 Selected applications of intrinsic Josephson junctions

Wang et al. (2001a, 2001b) have demonstrated the impressive performance of

their devices, like the response to microwaves up to the THz range. Additionally,

complex 2-D arrays, 3-D arrays and artiﬁcial shunted junctions with improved

synchronization have been realized leading to components and performance

required for applications, see Wang et al. (2002, 2003). Based on the high-quality

complex devices, a voltage standard using intrinsic junctions was proposed and

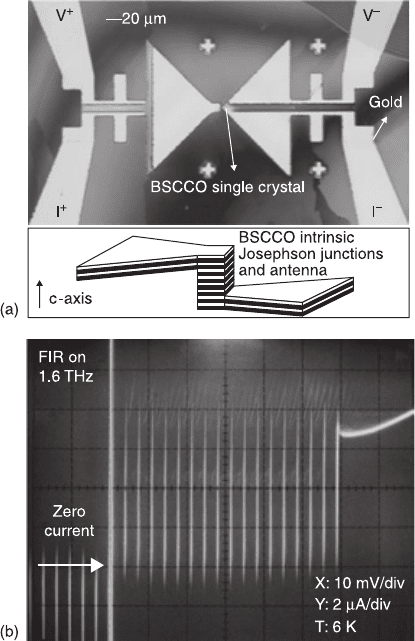
tested by Wang et al. (2001b, 2002, 2003). Zero-crossing Shapiro steps with

irradiation at 1.6 THz have been observed, Fig. 8.28. The ‘double sided fabrication

method’ was extended to 3-D stack arrays with up to 2500 intrinsic junction

stacks on a chip, Fig. 8.29. For a 256-stack array with about 11 000 junctions,

zero-crossing steps up to a voltage of 2.4 V have been observed. The advantage

8.27 Thin ﬁlm intrinsic Josephson junctions using a mesa-like geometry

(six mesas from 3 × 3 to 10 × 10 µm

) and electron beam cut Au electrodes

by IOP Publishing Ltd). Reprinted with permission from Seidel P, Schmidl

F, Pfuch A, Schneidewind H, and Heinz E (1996), ‘Investigations on high-T

thin ﬁlm intrinsic stacked Josephson junctions’, Supercond. Sci. Technol.

9, A9–A13, Fig. 2c, Copyright (1996) by IOP Publishing Ltd.



High-T

Josephson junctions 351

43X

would be the high working temperature which can be realized by liquid nitrogen

or a cryocooler leading to very compact voltage standards.

The use of intrinsic arrays as radiation sources up to some THz, i.e. especially

for the FIR range where such compact small sources can replace big CO

-laser

pumped systems, is restricted by the low power of emission of non-synchronized

arrays. Even if this power was enhanced by several µW within the last few years,

these sources are far from real applications.

8.28 Terahertz response of intrinsic Josephson junctions: (a) optical

image of a stack prepared out of a BSCCO single crystal with an

integrated bow-tie antenna (schematically shown at the bottom) and r.f.

ﬁlters all glued onto a silicon substrate; (b) zero-crossing Shapiro steps

under microwave irradiation of 1.6 THz (Wang et al., 2001a, Figs 1 and

3b, Copyright (2001) by the American Physical Society). Reprinted with

permission from Wang HB, Wu PH, and Yamashita T (2001a), ‘Terahertz

response of intrinsic Josephson junctions in high-T

superconductors’,

American Physical Society.

