Qiu X.G. (Ed.) High Temperature Superconductors
Подождите немного. Документ загружается.

70 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
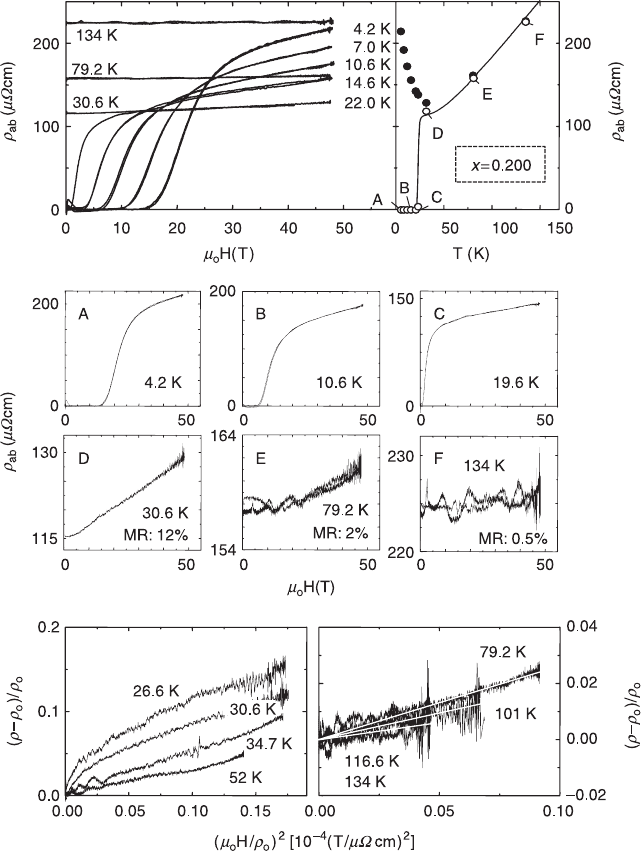
2.17 The left side of the upper frame gives an overview of the field
dependence of the in-plane resistivity
ρ
ab
(
µ
0
H) of La
1.8
Sr
0.2
CuO
4
at
different temperatures. The right side of the upper frame depicts the
temperature dependence of the in-plane resistivity
ρ
ab
(T) at zero magnetic
field (solid line). The open circles denote the values of the resistivity at
zero field, derived from pulsed field measurements; filled circles mark
the resistivity values at 45 T. For the positions labeled A, B, C, D, E and
F, the magnetoresistivity is shown in more detail in the middle part of
the figure. The magnetoresistivity at 45 T (MR) is indicated in percent
at T > T
c
. The lower frame shows the Kohler plots for the La
1.8
Sr
0.2
CuO
4
sample at selected temperatures used for the 48 T pulsed field data.
Transport properties of high-T
c
cuprate thin films 71
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
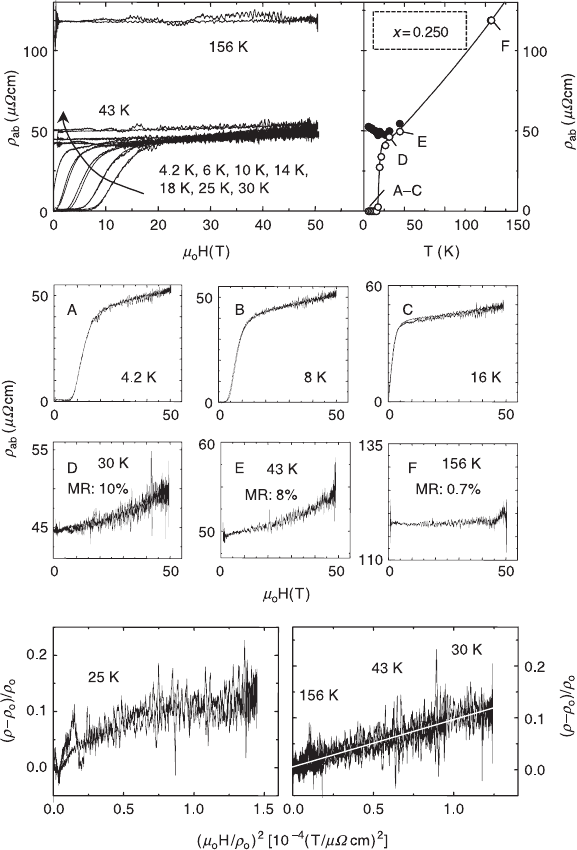
2.18 The left side of the upper frame gives an overview of the field
dependence of the in-plane resistivity
ρ
ab
(
µ
0
H) of La
1.75
Sr
0.25
CuO
4
at
different temperatures. The right side of the upper frame depicts the
temperature dependence of the in-plane resistivity
ρ
ab
(T) at zero magnetic
field (solid line). The open circles denote the values of the resistivity at
zero field, derived from pulsed field measurements; filled circles mark
the resistivity values at 45 T. For the positions labeled A, B, C, D, E and
F, the magnetoresistivity is shown in more detail in the middle part of
the figure. The magnetoresistivity at 50 T (MR) is indicated in percent at
T > T
c
. The lower frame shows the Kohler plots for the La
1.75
Sr
0.25
CuO
4
sample at selected temperatures used for the 50 T pulsed field data.
72 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
could be related to a weak pseudogap feature, present even in this compound, and
to disorder effects.
La
1.73
Sr
0.27
CuO
4
(x = 0.270, highly overdoped, superconducting)
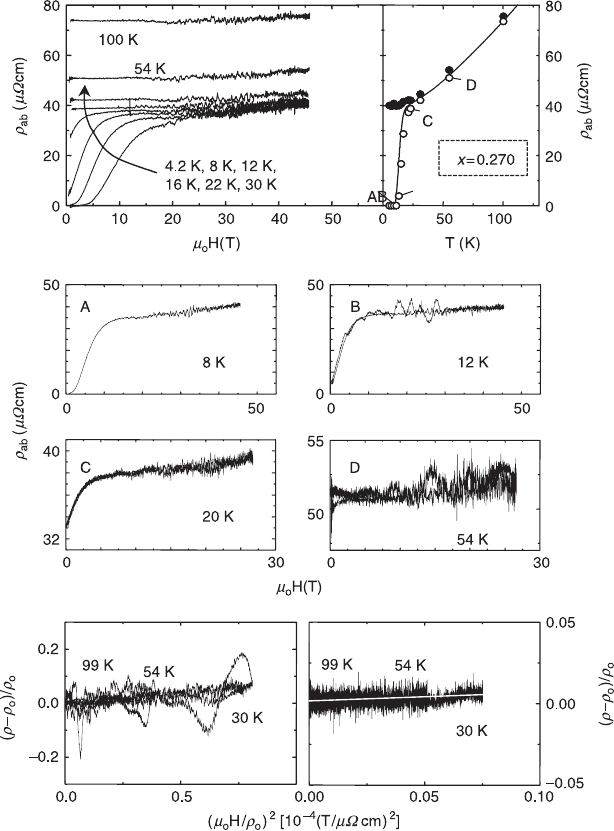
Finally, Fig. 2.19 gives the field dependent in-plane resistivity data of
La
1.73
Sr
0.27
CuO
4
(T
c
= 9.2 K), our strongest overdoped sample in this study. The
superconducting transitions are clear and sharp, just like in La
1.75
Sr
0.25
CuO
4
.
Since La
1.73
Sr
0.27
CuO
4
has, of all our samples, the lowest normal state resistivity,
the mechanical vibrations, caused by the high field-pulses, have a stronger impact
on its resistivity data. The effects of the vibrations, particularly present during the
lowering branch of the pulse, are clearly visible in the data taken at 12 K and
54 K, respectively, shown in graphs B and D in Fig. 2.19. The other
magnetoresistivity curves presented in Fig. 2.19 contain only the data taken
during increasing magnetic field for clarity. In contrast with the previous samples,
the
ρ
ab
(
µ
o
H)-curves of La
1.73
Sr
0.27
CuO
4
do not cross each other at fields below
45 T. Above T
c
, the magnetic field dependencies of the resistivity are essentially
quadratic, thus without tendency towards saturation.
In the field and temperature range used in our experiments, the magnetoresistivity
is positive for all our films, in agreement with the results of (Harris et al. 1995,
Kimura et al. 1996, Malinovski et al. 1997). Our data on thin films differ from the
results of references (Ando et al. 1995, Boebinger et al. 1996) on single crystals
of La
2 – x
Sr
x
–CuO
4
with x = 0.08 and x = 0.13, where the magnetoresistivity in the
limit of high fields was found to be negative.
Influence of the normal state magnetoresistivity for (strongly) overdoped
La
2 – x
Sr
x
CuO
4
The lower frames of Fig. 2.17–2.19 present the Kohler plots for the overdoped
samples La
1.8
Sr
0.2
CuO
4
(T
c
= 22.8 K), La
1.75
Sr
0.25
CuO
4
(T
c
= 15.6 K) and
La
1.73
Sr
0.27
CuO
4
(T
c
= 9.2 K). We see that the part of the magnetoresistivity,
which has no quadratic behavior with respect to the applied field diminishes upon
increasing the charge carrier concentration and finally becomes undetectable in
the La
1.73
Sr
0.27
CuO
4
sample.
This observation can be consistently interpreted in the context of our previous
results that the one-dimensional character of the charge transport (stripes) fades
away upon doping (Vanacken et al. 2001). As the effective dimensionality of the
electrical transport increases from 1D to 2D (or 3D), the fluctuations become
indeed less pronounced.
So far, we have ignored the part of the magnetoresistivity that appears in a
Kohler plot as a straight line. In Fig. 2.19, we see that magnetic field dependencies
of the La
1.73
Sr
0.27
CuO
4
data are essentially H
2
up to 45 T. Moreover, the straight
lines coincide, which implies that H/
ρ
o
scales the magnetoresistivity and hence
Transport properties of high-T
c
cuprate thin films 73
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
2.19 The left side of the upper frame gives an overview of the field
dependence of the in-plane resistivity
ρ
ab
(
µ
0
H) of La
1.73
Sr
0.27
CuO
4
at
different temperatures. The right hand side of the upper frame depicts
the temperature dependence of the in-plane resistivity
ρ
ab
(T) at zero
magnetic field (solid line). The open circles denote the values of the
resistivity at zero field, derived from pulsed field measurements; filled
circles mark the resistivity values at 45 T. For the positions labeled
A, B, C and D, the magnetoresistivity is shown in more detail in the
middle part of the figure. The lower frame shows the Kohler plots for
the La
1.73
Sr
0.27
CuO
4
sample at selected temperatures used for the 45 T
pulsed field data (left side) and the 12 T pulsed field data (right side).
74 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
that the classical Kohler’s rule is valid in La
1.73
Sr
0.27
CuO
4
. Its magnetoresistivity
can safely be attributed to the normal state. The data for the other strongly
overdoped sample, La
1.75
Sr
0.25
CuO
4
, follows Kohler’s rule above 30 K. For the
superconducting samples with a lower Sr content (Fig. 2.13 to 2.17, lower frames),
the dependence with (H/
ρ
o
)
2
remains linear over a wide temperature range (far
above T
c
) but the slopes increase when lowering the temperature. The deviations
are more pronounced in the underdoped samples. Many authors observed this
apparent violation of Kohler’s rule in high-T
c
systems and speculated on its origin
(Lacerda et al. 1994, Harris et al. 1995, Kimura et al. 1996, Semba and Matsuda
1997, Balakirev et al. 1998, Abe 1999). In early reports, it was assumed that the
violation of Kohler’s rule reflected the influence of superconducting fluctuations
(Kimura et al. 1996, Semba and Matsuda 1997). However, the observed
temperature and field dependencies could not be reproduced by any fluctuation
theory.
Since the contrast of the stripes with respect to their surrounding decreases
upon doping (Fig. 2.8), the dimensionality of the charge-transport in the overdoped
samples is not well defined. Although La
1.8
Sr
0.2
CuO
4
and La
1.75
Sr
0.25
CuO
4
reveal
distinct pseudogap features, they partially recover a 2D (or 3D) character. It is
therefore not surprising that the magnetoconductivity of the overdoped samples
could not be fitted with a simple power law with respect to the temperature.
Moreover, as follows from the data on La
1.73
Sr
0.27
CuO
4
, the normal-state
contribution to the magnetoresistivity cannot be neglected in samples with a high
doping level. At the moment, however, there is no theory available showing an
accurate evaluation of this normal-state background. It is even not ‘a priori’ clear
whether the violation of Kohler’s rule should be attributed to fluctuations or to the
normal state (or to both). For example, if the mobile stripes bend in a magnetic
field, they may influence the normal state magnetoresistivity in an unconventional
way. In this context, we would like to mention the result of Ando and co-workers
(Ando et al. 1999), who have reported a possible influence on the striped structure
in non-superconducting underdoped cuprates by a magnetic field, in the
configuration where the magnetic field is applied parallel to the ab-plane. Kimura
et al. (Kimura et al. 1996) found a strong suppression of the magnetoresistivity in
La
2 – x
Sr
x
CuO
4
around the hole concentration with x = 1/8, a concentration that is
related to a more static nature of the stripes (Tranquada et al. 1995). Their results
underline the importance of the striped structure in the analysis of magnetoresistivity
measurements.
Role of the pseudogap and pre-formed pairs
The pseudogap is emerging as an important indicator revealing the nature of the
superconductivity as well as the normal state in high-T
c
samples. A possible
scenario relates the pseudogap with the presence of electronic pair states far above
T
c
(Tranquada et al. 1995, Randeria 1997, Bianconi et al. 1998, Maly et al. 1998,
Transport properties of high-T
c
cuprate thin films 75
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
Emery 1999, Zaanen 1999, Moshchalkov et al. 1999, Vanacken et al. 2001). The
idea is that Cooper pairs are already formed at a temperature T* far above T
c
, but
bulk phase coherent superconductivity is only established when long-range phase
coherence is achieved below T
c
. The models, which are based on this precursor
superconductivity scenario, get experimental growing support. Scanning tunneling
spectroscopy measurements clearly demonstrate that the pseudogap evolves into
the superconducting gap at low temperatures (Kugler et al. 2001). Moreover,
ARPES data indicate that the pseudo- and the superconducting gap both have
d-wave symmetry (Loeser et al. 1996). Our experimental observation of a close
relation between the pseudogap and the superconducting fluctuations (= precursor
pairs) strongly favor these models as well. Altshuler et al. (Altshuler et al. 1996)
questioned the interpretation of the pseudogap as the superconducting gap because
a large fluctuation diamagnetism has not been observed between T
c
and T*. Emery
et al. [1999] stated however that the absence of strong diamagnetic effects is
expected if the superconducting fluctuations are one-dimensional, and if the
Josephson coupling between stripes is weak. In this case, an applied magnetic
field does not cause any significant orbital motion until full phase coherence
develops, close to T
c
.
The magnetoresistivity data for La
1.9
Sr
0.1
CuO
4
, presented in Fig. 2.16, do not
show either clearly marked second critical fields H
c2
(T) or saturation at high
fields. Fluctuating Cooper pairs seem to exist up to very high fields, most probably
above the field range accessible by our pulsed field setup. Following the ideas
outlined in (Emery 1999, Kugler et al. 2001), T* is the mean-field critical
temperature of the superconductor rather than T
c
. When T* is used to obtain the
paramagnetic limiting field for sample La
1.9
Sr
0.1
CuO
4
(T* ≈ 400 K, T
c
= 17.5 K)
instead of T
c
, a value of
µ
o
H
p
≈ 700 T is obtained, illustrating that a field of 50 T
is indeed not high enough to destroy completely the preformed pairs. The ARPES
study by Loeser et al. of the pseudogap state in Bi
2
Sr
2
CaCu
2
O
8 +
δ
(Loeser et al.
1996) revealed a binding energy of 75 meV in the precursor pairs. Thus a magnetic
field of about 130 T (
µ
o
µ
B
H = k
B
T) would be needed to destroy them completely.
If the idea of precursor pairs is correct, the temperature seems to be a much more
critical parameter for the existence of the pairs than a magnetic field up to 50 T.
The ‘resistive upper critical field’, as defined by a line construction, is certainly a
questionable concept with respect to the underdoped high-T
c
compounds. It is
possible that the magnetoresistivity data of the samples, which show a pseudogap
behavior, just reflect the behavior maybe even the localization, and of the precursor
pairs in a magnetic field.
Superconductivity in metals is the result of two distinct quantum phenomena,
pairing and long-range phase coherence. The influence of the stripes on
superconductivity is therefore two-fold. First of all, the one-dimensional character
of the charge transport favors pair formation as follows from the similarities
between the pseudogap in high-T
c
superconductors and the spin-gap in ladder
cuprates and from experiments that demonstrate a connection between the
76 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
superconducting- and the pseudogap properties. On the other hand, the low
dimensionality hinders the long-range phase coherence needed to establish bulk
superconductivity. It is a well-known fact that long-range phase coherence is
impossible in a purely one-dimensional system. This is in agreement with the
observation that (La,Sr,Ca)
14
Cu
24
O
41
, the only known superconducting ladder
compound, becomes superconducting under high pressure when the interactions
between the ladders are enhanced.
As already stated above, the broadening of the superconducting transitions in
underdoped cuprates, both in field and temperature, is most probably due to
sample inhomogeneities. However, in this case the inhomogeneities do not reflect
a bad sample quality but rather an intrinsic property, related to a low charge carrier
concentration and the presence of stripes (intrinsic phase separation).
Generic phase diagram including fluctuation area
The pulsed field transport measurements at temperatures T > T
c
revealed a sudden
appearance of a large positive in-plane magnetoresistivity in La
2 – x
Sr
x
CuO
4
close to the insulator-superconductor transition at x = 0.055. This suggests that
the effect can be attributed to superconducting fluctuations. The fluctuations
appear at temperatures which exceed T
c
by several times. It is therefore reasonable
to speak about precursory pairing far above T
c
. By presenting the magnetoresistivity
data in the form of classical Kohler-plots, we found that the superconducting
fluctuations are very pronounced in underdoped samples. At the same time, the
normal-state contribution to the magnetoresistivity dominates in overdoped
samples. The region where we observed superconducting fluctuations is
schematically shown in the phase diagram of Fig. 2.20 by the shaded area. In
order to evaluate this region exactly, an adequate theory is needed which allows
the separation of fluctuations and normal-state contributions to conductivity.
However, it is clear from our data that there is a close link between the presence
of strong superconducting fluctuations and the pseudogap phase. Since fluctuations
are expected to become more pronounced in systems with a reduced dimensionality,
the following section will deal with this analysis.
Fluctuation analysis of underdoped La
2 – x
Sr
x
CuO
4
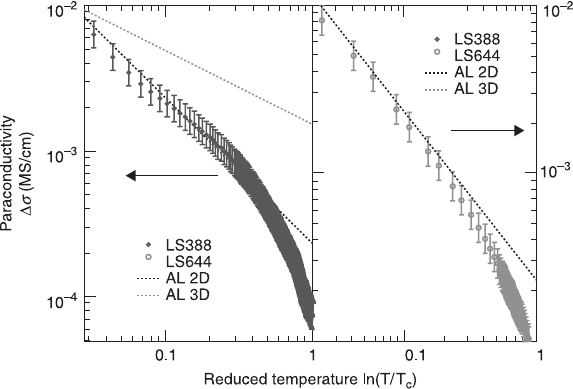
To find the correct fluctuation dimensionality of our system, a typical plot can be
used (Fig. 2.21). On the x-axis,
ε
= ln(T/T
c
) is plotted and on the y axis the log of
the difference in conductivity, the paraconductivity =
σ
50T
–
σ
0T
. If
ε
is small, i.e.
near the transition temperature, then
ε
is equal to (T – T
c
)/ T
c
. For the 2D
fluctuations, in accordance with the Lawrence-Doniach model (Lawrence and
Doniach 1971), a distance between the Cu-O planes is chosen, d = 6.6Å. This
distance is almost doping independent. For both the 1D and 3D fluctuations, a
zero level adjustment can be done by choosing the correct
ξ
. It can be seen that ∆
σ

Transport properties of high-T
c
cuprate thin films 77
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
2.20 The same (T,x)-phase diagram of the La
2 – x
Sr
x
CuO
4
samples as
shown in Fig. 2.2. The Néel phase is omitted for clarity. Region III,
bordered by the T
MI
line, labels the insulating region of the phase
diagram. Region III is divided into two parts by a gray line. On the left
side of the gray line, variable range hopping conductivity characterizes
the insulating phase. On the right side of the gray line the diverging
resistivity upon a temperature decrease can be described by
ρ
(T) ~
ln(1/T) or a power law. The shaded region above the superconducting
region (SC) depicts the fluctuation area.
data show a good agreement with the 2D AL-fluctuations, not only with the slope,
but also the exact value between
ε
= 0.02 and
ε
= 0.2 is obtained. In the original
paper (Aslamazov and Larkin 1968), the coherence length
ξ
is considered to be
larger than the sample thickness. This is, however, not the case in the samples we
used. What could happen is that the superconducting carriers only flow completely
inside the Cu-O planes if the temperature is low enough (
ξ
≤ t and
ξ
≤ d). Then,
the coherence length should be bigger than the thickness where the superconducting
carriers flow and the 2D formula should be valid. Indeed, taking the results
presented in Fig. 2.21, the experimental data fit quite well to the 2D AL formula,
indicating the fluctuations are of the two-dimensional type. This might look like a
contradiction to the fact that we rather expect the normal state transport mechanism
in these underdoped material to be 1D, but when superconductivity occurs, the 1D
normal conductivity paths (stripes) seem to couple to allow the appearance of the
2D superconductivity.
78 High-temperature superconductors
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
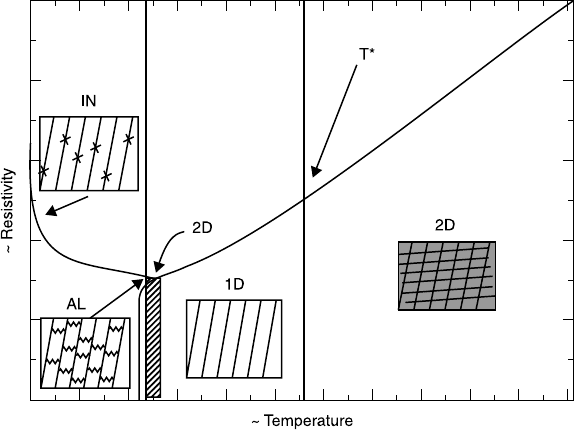
2.3.4 Conclusion: temperature dependence of the
resistivity
After studying the field induced normal state conductivity and the superconducting
fluctuations, we are now able to describe the effective dimensionality of the
normal state conductivity and the superconducting state. In Fig. 2.22, we show
schematically the different charge order states in the Cu-O planes at different
temperature regions. The resistivity
ρ
(T) shows a transition at T*(x) from a linear
to a superlinear temperature dependence. In the model proposed by Moshchalkov
et al. (Moshchalkov 1999; Moshchalkov et al. 1999, 2001; Vanacken et al. 2001),
this corresponds, respectively, to a two- and a one-dimensional conductivity. At
low temperatures T < T*, a stripe structure (1D) is observed, while at high
temperatures T > T*, the charges have enough thermal energy to also flow in
the interstripe region (2D). When the temperature is close to T
c
, the stripes
become coupled, resulting in 2D-superconductivity. In the vicinity of T
c
, the
superconducting fluctuations show a two-dimensional Aslamasov–Larkin behavior
(AL). At temperatures lower than T
c
, a magnetic field has to be applied to
investigate the field-induced normal state. This magnetic field also suppresses the
inter-stripe coupling. Hence the stripe structure is recovered, but due to the low
temperatures and the impurities, the charges become localized. An insulating-like
behavior is thus found for
ρ
(T→0) (IN) in high magnetic fields.
2.21 The paraconductivity as a function of the reduced temperature
for samples with x = 0.08 and x = 0.09. Both samples closely follow
the dotted AL 2D lines, and are distinctly different from the dashed
3D AL line.
Transport properties of high-T
c
cuprate thin films 79
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
20
1
2
3
4
5
6
7
8
9
30
1
2
3
4
5
6
7
8
9
40
1
2
43X
© Woodhead Publishing Limited, 2011
2.4 Hall effect
In this section, the Hall number and its field and temperature dependencies are
investigated. The Hall coefficient data are discussed and the magnetic field
dependence of the Hall coefficient is analyzed. The carrier concentration will be
derived, followed by derivations of Hall mobility, Hall angle and Hall conductivity.
Then, a scaling with the pseudogap energy is used to analyze the temperature
dependence of the Hall coefficient data for different doping levels in a similar way
as is done for the resistivity.
2.4.1 Introduction
The Hall effect (Hall 1879) can provide valuable information about the electronic
structure of the high-T
c
superconductors. In this introduction, the origin of the
Hall effect is reviewed both in the normal state at temperatures T >> T
c
and in the
mixed state at temperatures close to T
c
. We describe below the field dependence
of the Hall resistivity
ρ
H
(
µ
o
H) of our La
2 – x
Sr
x
CuO
4
thin films in steady magnetic
fields up to 10 T and in pulsed magnetic fields up to 50 T. The data obtained on
the underdoped samples reveal clear evidence for the presence of strong
superconducting fluctuations, in agreement with the results presented in
section 2.4.2.
2.22 The different effective dimensionalities of high T
c
cuprates in the
resistivity–temperature plane.
