Романовский С.И. Седиментологические основы литологии
Подождите немного. Документ загружается.


метод квантилей разработан с целью
приближенной
графической
оценки
требуемых статистик.
Выбор
того или иного метода
оценки
перечисленных выше
статистических характеристик эмпирических распределений опре-
деляется исходной шкалой, в которой выражены результаты гра-
нулометрического анализа, и требуемой точностью оценивания.
В
ряде случаев, когда статистики рассчитываются с целью их
последующего изображения на генетических диаграммах, исполь-
зуют
оба метода и путем последовательного перебора найденных
характеристик фракционного состава добиваются наилучшего
разделения обстановок осадконакопления. Сразу же отметим, что
если таким путем разделяются современные обстановки, то в гео-
логическом аспекте эта задача тривиальна и особого смысла не
имеет, поскольку
найденная
комбинация статистических харак-
теристик будет иметь реальный смысл только для конкретгых
(опробованных) обстановок осадконакопления и потеряет свою
значимость дая^е для одноименных (но не опробованных) обстано-
вок
осадконакопления, а потому актуалистический подход не
поможет выявить требуемую комбинацию статистик с целью
реставрации обстановок
накопления
осадков геологического прош-
лого.
Если разделяются палеообстановки, то без использования
других лито логических и палеонтологических признаков, т. е.
без
внешнего контроля, истинность решения данной задачи оста-
нется недоказуемой *.
Рассмотрим последовательно оба метода оценивания. Метод
приближенных квантильных оценок разработан применительно
к Ф-шкале Крамбейна. Наиболее распространен этот метод в тех
странах, где принято изображать результаты гранулометрических
анализов в Ф-единицах. Первоначально эти
оценки
были пред-
лояч
р
ены П. Траском. В. Крамбейном, Ф. Петтиджоном, Г. Отто
и другими геологами. Однако в настоящее время их формулы
практически не используются. Зато весьма популярны квантиль-
ные статистики Д. Л. Инмана
[4331,
которые впоследствии модифи-
цировали (в плане усложнения) Р. Л. Фолк и В. С. Уард
[4021.
Некоторые примеры квантильных оценок среднего размера зерен,
стандартного отклонения, асимметрии и эксцесса приведены
в
табл. 4. Ясно, что эти 4 характеристики являются основными
не только потому, что они имеют однозначпую статистическую
интерпретацию, но и в связи с тем, что те же показатели могут
рассчитываться с помощью метода моментов, что дает возмояшость
сравнивать результаты, полученные разными методами.
Однако квантильный метод оценивания позволяет помимо
отмеченных 4 характеристик фракционного состава вычислять
практически неограниченное количество других мер, статисти-
ческий
смысл и содержательная интерпретация которых, как
правило, не обосновываются. К числу таких мер можно отнести
*
Более подробно
данный
тезис будет обоснован в гл. VII.
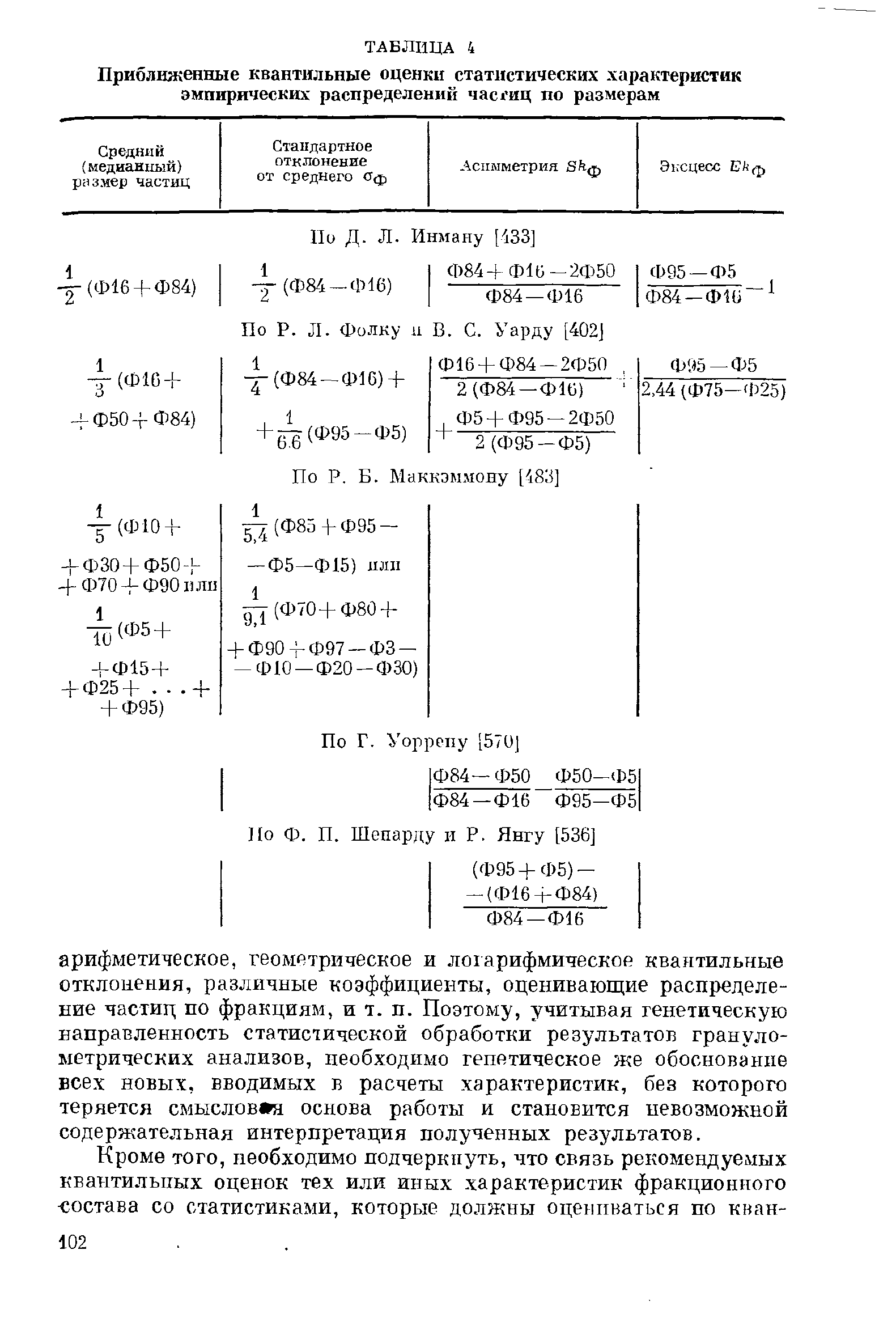
ТАБЛИЦА
4
Приближенные
квантильные
оценки
статистических
характеристик
эмпирических
распределений
часшц
по
размерам
арифметическое, геометрическое и логарифмическое квантильные
отклонения, различные коэффициенты, оценивающие распределе-
ние частиц по фракциям, и т. п. Поэтому, учитывая генетическую
направленность статистической обработки результатов грануло-
метрических анализов, необходимо гепетическое же обоснование
всех
новых, вводимых в расчеты характеристик, без которого
теряется смысловая основа работы и становится невозможной
содержательная интерпретация полученных результатов.
Кроме
того,
необходимо подчеркнуть, что связь рекомендуемых
кваитильных оценок тех или
иных
характеристик фракционного
состава
со статистиками, которые должны оцениваться по кван-
тилям, не всегда очевидна и в ряде случаев требует специального
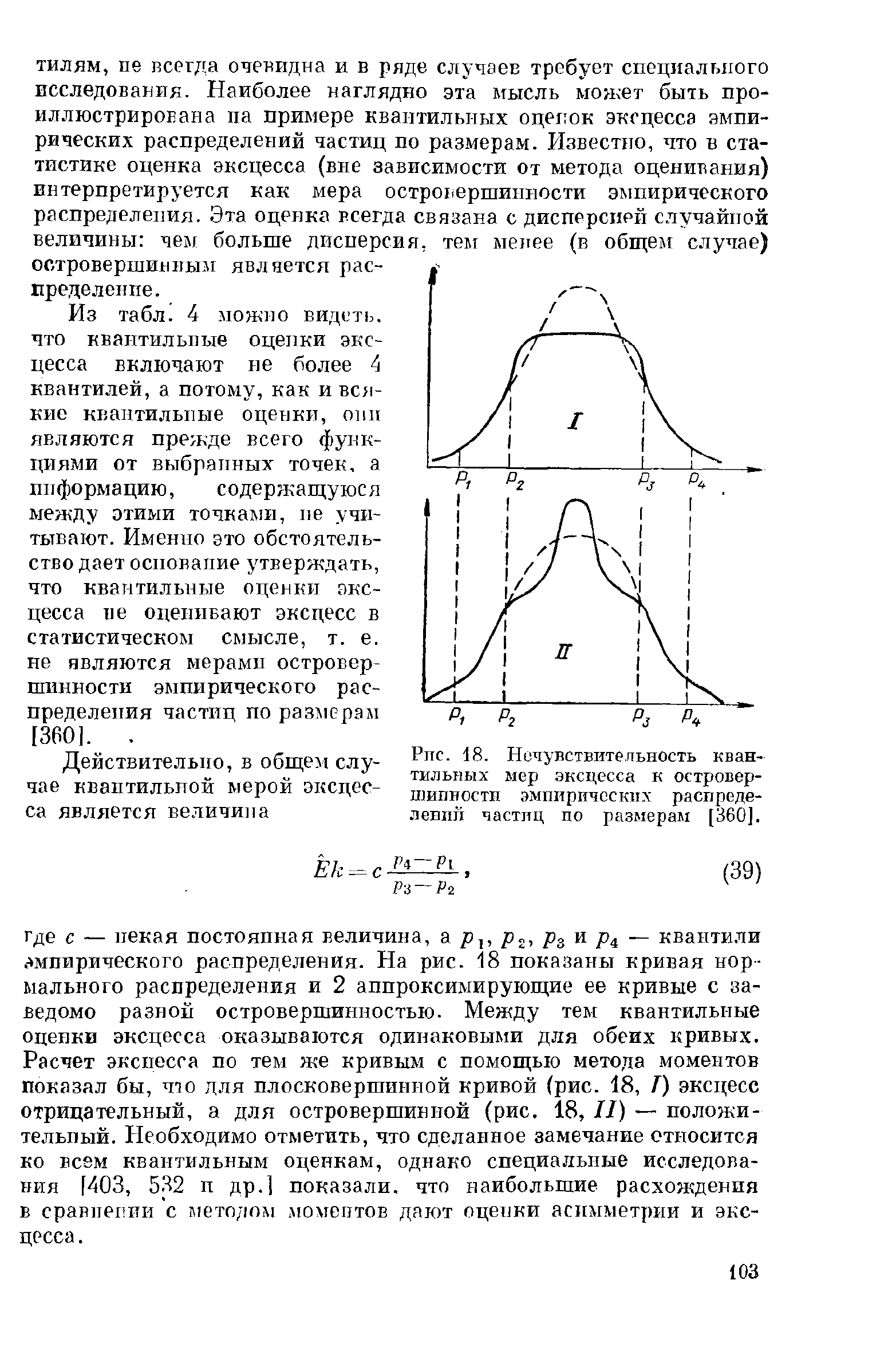
исследования. Наиболее наглядно эта мысль может быть про-
иллюстрирована па примере квантильных оценок эксцесса эмпи-
рических распределений частиц по размерам. Известно, что в ста-
тистике оценка эксцесса (вне зависимости от метода оценивания)
интерпретируется как мера островершинности эмпирического
распределения. Эта оценка всегда связана с дисперсией случайной
величины: чем больше дисперсия, тем менее (в общем случае)
островершинным является
рас-
пределение.
Из табл. 4 можно видеть,
что квантильиые
оценки
экс-
цесса
включают не более 4
квантилей, а потому, как и вся-
кие квантильиые оценки, они
являются
прелюде
всего функ-
циями
от выбранных точек, а
информацию, содержащуюся
между этими точками, не
учи-
тывают.
Именно это обстоятель-
ство
дает основание утверждать,
что квантильиые
оценки
экс-
цесса
не оценивают эксцесс в
статистическом смысле, т. е.
не являются мерами островер-
шинности эмпирического рас-
пределения частиц по размерам
[360].
.
Действительно, в
Общем
слу-
Рпс
-
18
* Нечувствительность кван-
^
о « тильных мер эксцесса к островер-
чае квантильнои мерой эксцес- шитгост
эмпирических
распреде-
са
является величина
ленип
частиц по размерам
[360].
Ek
= с
p
*~
Pl
,
Р3 —
Р2
(39)
где с — некая постоянная величина, а р,, р
2
, р
3
и /?
4
— квантили
эмпирического распределения. На рис. 18 показаны кривая нор-
мального распределения и 2 аппроксимирующие ее кривые с за-
ведомо
разной островершинностью. Между тем квантильиые
оценки
эксцесса оказываются одинаковыми для обеих кривых.
Расчет
экспесса по тем же кривым с помощью метода моментов
показал
бы, чю для плосковершинной кривой (рис. 18, T) эксцесс
отрицательный, а для островершинной (рис. 18, LT) — положи-
тельный. Необходимо отметить, что сделанное замечание относится
ко всем квантильным оценкам, однако специальные исследова-
ния [403, 532 и др.] показали, что наибольшие расхождения
в
сравнении с методом моментов дают
оценки
асимметрии и экс-
цесса
.

Резонным является следующий вопрос: коль скоро квантиль-
иые меры являются функциями от выбранных точек, то каково
оптимальное число этих точек, чтобы квантильиые оценки были
максимально эффективными? Эффективность в данном случае
понимается в чисто статистическом смысле, т. е. оценка является
максимально эффективной, если дисперсия этой оценки мини-
мальна.
Анализ этого вопроса в отношении квантильных оценок
среднего размера зерен и сортированности осадка проведен
Р. Б. Маккэммоном
[483].
Идея его подхода заключается в
срав-
нении
предлагаемых мер с оценками тех же характеристик для
нормального распределения. Моячно, конечно, критиковав такой
метод
оценивания эффективности на том основании, что размеры
зерен далеко не всегда распределены по нормальному закону.
Однако это единственно возможный путь, позволяющий конструк-
тивно решить поставленную задачу. Поясним практическую
реализацию идеи Р. Б. Маккэммоиа па примере оценки эффектив-
ности квантильпой меры среднего размера зерен.
Предположим, что фракционный состав осадка является вы-
боркой из нормального распределения N (а, а). Тогда известно,
что эффективной оценкой параметра а (математического ожидания)
является х (средний размер
«зерен).
Пусть далее медиана, т. е.
квантиль Ф50, является оценкой х. Необходимо определить
эффективность медианы как оценки среднего размера зерен.
Из курса математической статистики мы знаем (см., напри-
мер,
[280]),
что медиана распределена асимптотически нормально
с
дисперсией а
2
л/2тг), а среднее распределено нормально с дис-
персией
o
2
in.
Поэтому, исходя из определения эффективности,
легко находим, что эффективность медианы как оценки среднего
составляет
^1:^. =
1.^^0/
(40)
Пользуясь
данным приемом, можно оценить эффективность кван-
тильных мер среднего размера зерен, приведенных в табл, 4.
Так.
мера Д. Л. Инмана имеет эффективность 74%, мера
Р. Л.
Фолка
и В. С. Уарда — 88%, а меры Р. Б. Маккэммона
соответственно
93 и 97%. Из этих оценок вытекает следующее
очевидное заключение: квантильиые меры статистических харак-
теристик эмпирических распределений частиц по размерам тем
более
эффективны, чем большее число квантилей вовлечено в их
^расчеты.
Причем всегда существует оптимальное число квантилей,
увеличение которого уже практически не приводит к повышению
эффективности оценок.
Метод
моментов в отличие от приблия^енного метода квантилей
использует
всю информацию, содерялащуюся в эмпирическом
распределении частиц по фракциям. Мы не будем в данном случае
приводить расчетные формулы для оценки среднего размера
зерен,
стандартного отклонения, асимхметрии и эксцесса. Они
содержатся в любом учебнике по математической статистике и при-
менительно к гранулометрическому анализу воспроизведены в мо-
нографиях Л. Б. Рухина [258] и В. Н. Шванова
[3321.
Отметим
лишь, что при использовании метода моментов величина
оценки
зависит
от того, на сколько фракций разбит весь диапазон изме-
нения
размеров частиц. Причем величина погрешности прямым
образом
связана с видом теоретической
функции
распределения,
которой аппроксимируются данные гранулометрического анализа.
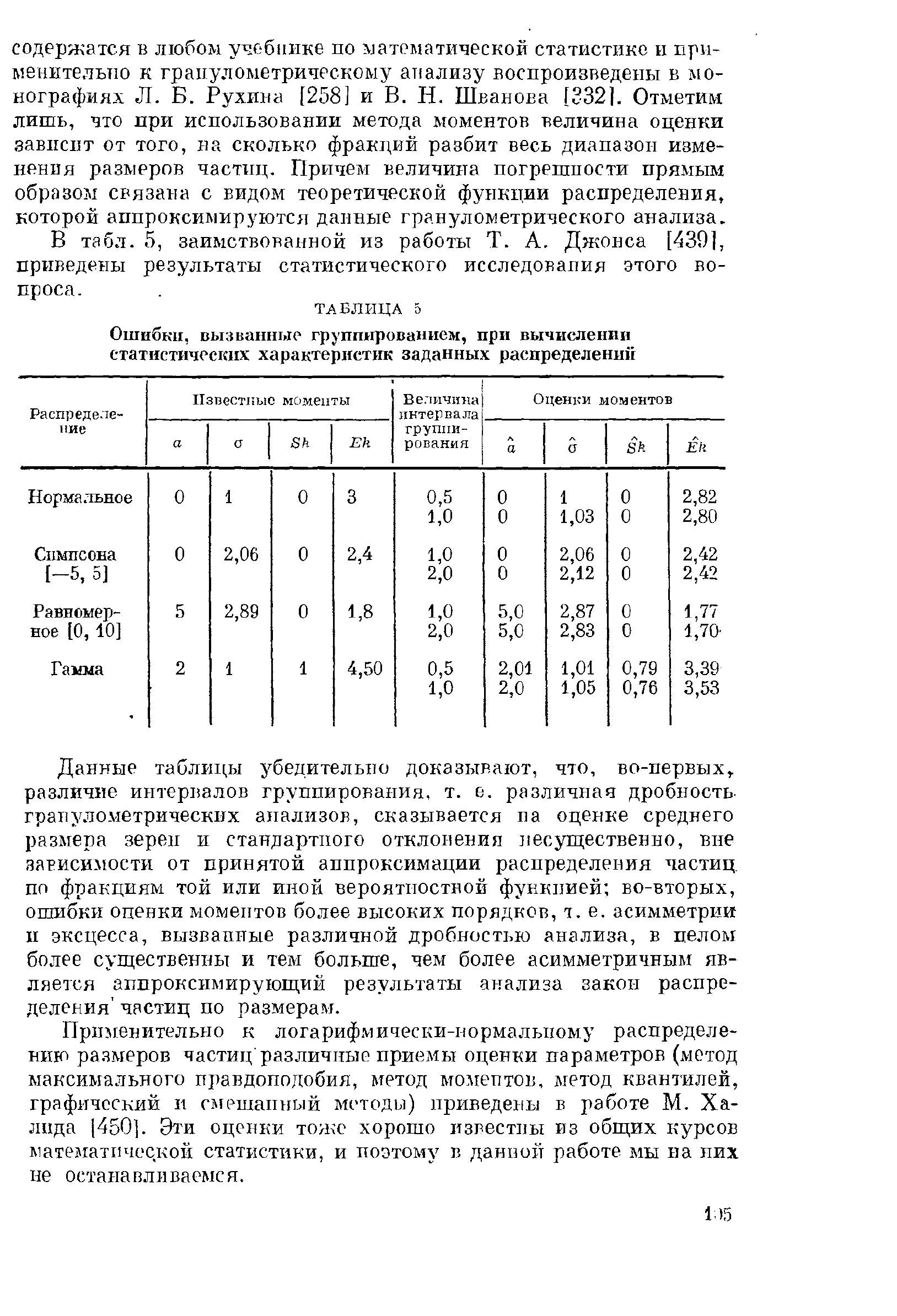
В
табл. 5, заимствованной из работы Т. А. Джонса
[4391,
приведены результаты статистического исследования этого во-
проса.
ТАБЛИЦА
5
Ошибки,
вызванные
группированием,
при
вычислении
статистических
характеристик
заданных
распределений
Распределе-
I
Известные
моменты
Величина
интервала
Оценки
моментов
ние
группи-
о
о
Sk Ek
рования
л
а
л
а
Sk
Ek
Нормальное
0
1
0
3
0,5
0
1 0
2,82
Нормальное
1,0 0 1,03 0
2,80
Спмпсона 0
2,06
0
2,4
1,0
0 2,06 0
2,42
[-5, 5] 2,0 0
2,12
0
2,42
Равномер-
5
2,89
0
1,8
1,0
5,0
2,87 0 1,77
ное [0, 40] 2,0 5,0 2,83 0 1,70
Гамма
2
1 1
4,50
0,5
2,01
1,01 0,79 3,39
Щ
1,0 2,0 1,05 0,76 3,53
Данные таблицы убедительно доказывают, что, во-первых,,
различие интервалов группирования, т. е. различная дробность
гранулометрических анализов, сказывается на оценке среднего
размера
зерен и стандартного отклонения несущественно, вне
зависимости от
принятой
аппроксимации распределения частиц,
по фракциям той или
иной
вероятностной функцией; во-вторых,
ошибки
опенки
моментов более высоких порядков, т.е. асимметрии
и эксцесса, вызванные различной дробностью анализа, в пелом
более существенны и тем больше, чем более асимметричным яв-
ляется аппроксимирующий результаты анализа закон распре-
деления' частиц по размерам.
Применительно к логарифхмически-нормалыюму распределе-
нию размеров частиц различные приемы
оценки
параметров (метод
максимального правдоподобия, метод момептов, метод квантилей,
графический и смешанный методы) приведены в работе М. Xa-
лида
[450].
Эти
оценки
тояхо хорошо известны из общих курсов
математической статистики, и поэтому в данной работе мы на них
не останавливаемся.
1)5
Таким образом, резюмируя изложенные выше соображения,
можно заключить, что в целом
оценки
статистических характери-
стик распределения частиц по фракциям, полученные с помощью
метода моментов, должны быть предпочтительнее приближенных
квантильных оценок. Причем чем выше порядок оцениваемого
момента, тем различия между этими двумя методами становятся
более существенными. В. Д. Сэвон
[532J
по данным более 300 об-
разцов песчаных осадков рассчитал коэффициенты
корреляции
ме;кду статистиками,
найденными
с помощью различных методов.
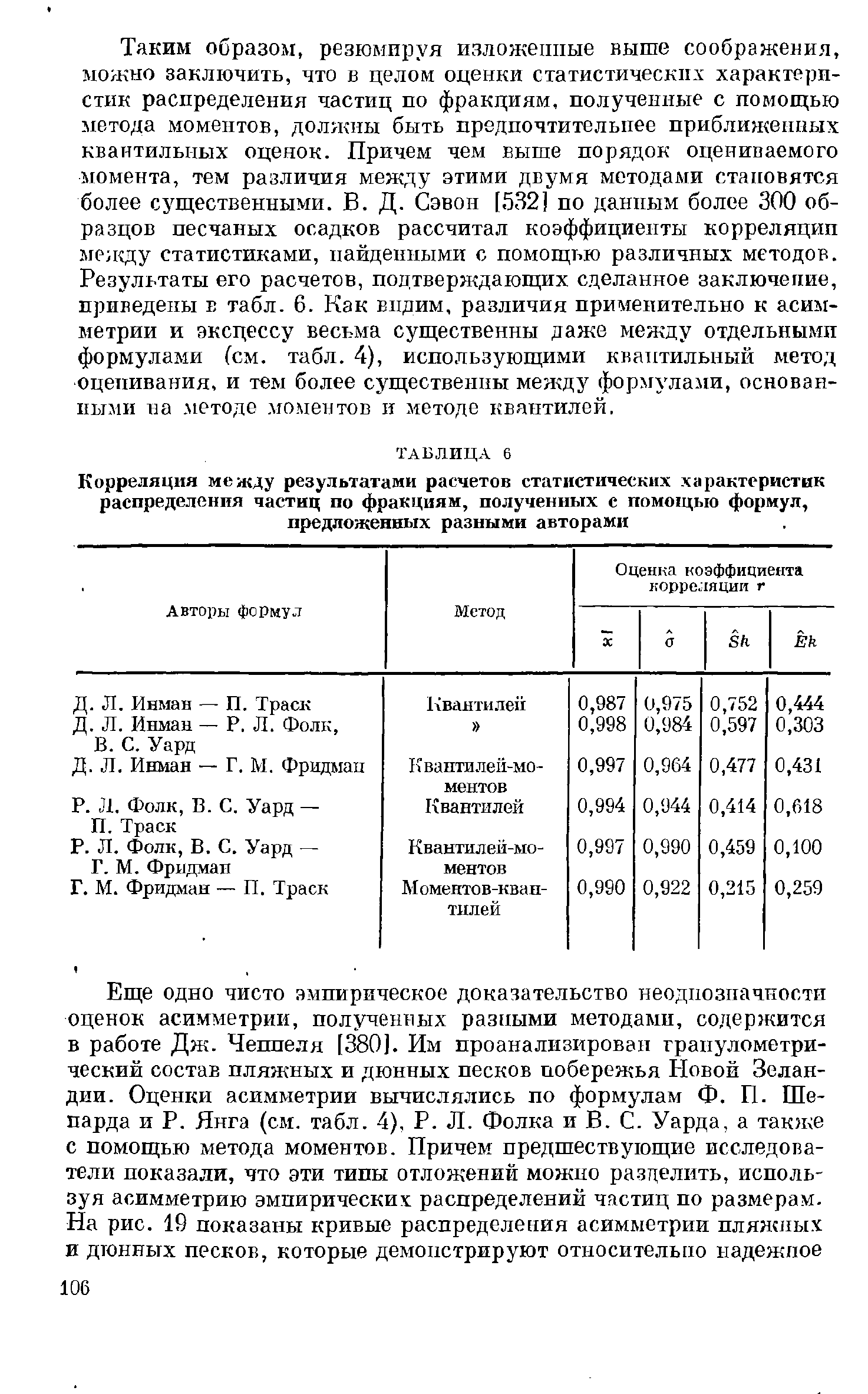
Результаты его расчетов, подтверждающих сделанное заключение,
приведены в табл. 6. Как видим, различия применительно к асим-
метрии и эксцессу весьма существенны даже между отдельными
формулами (см. табл. 4), использующими кваитильный метод
оценивания, и тем более существенны между формулами, основан-
ными на методе моментов и методе квантилей.
ТАБЛИЦА
6
Корреляция
между
результатами
расчетов
статистических
характеристик
распределения
частиц
по
фракциям,
полученных
с
помощью
формул,
предложенных
разными
авторами
Оценка
коэффициента
•
корреляции
г
Авторы формул
Метод
ОС
о
Sk
Ek
Д. Л. Инман — П. Траск
Квантилей
0,987
0,975 0,752
0,444
Д. Л. Инман — Р. Л. Фолк,
»
0,998 0,984 0,597 0,303
В.
С. Уард
0,998 0,984 0,597 0,303
Д. Л. Инман — Г. М. Фридман
К
ванти лей-мо- 0,997 0,964 0,477 0,431
ментов
Р. Л. Фолк, В. С. Уард — Квантилей 0,994 0,944 0,414 0,618
П.
Траск
0,994 0,944 0,414 0,618
Р. Л. Фолк, В. С. Уард — Квантилей-мо- 0,997 0,990 0,459 0,100
Г.
М. Фридман ментов
0,997 0,990 0,459 0,100
Г.
М. Фридман — П. Траск Моментов-кван- 0,990 0,922 0,215 0,259
тилей
Еще
одно чисто эмпирическое доказательство неоднозначности
оценок асимметрии, полученных разными методами, содержится
в
работе Дж. Чеппеля
[380].
Им проанализирован гранулометри-
ческий
состав пляжных и дюнных песков побережья Новой Зелан-
дии.
Оценки
асимметрии вычислялись по формулам Ф. П. Ше-
парда и Р. Янга (см. табл. 4), Р. Л. Фолка и В. С. Уарда, а также
с помощью метода моментов. Причем предшествующие исследова-
тели показали, что эти типы отложений можно разделить, исполь-
зуя асимметрию эмпирических распределений частиц по размерам.
На рис. 19 показаны кривые распределения асимметрии пляжных
и дюнных песков, которые демонстрируют относительно надежное

разделение этих генетических типов, отложений по данным асим-
метрии, вычисленной только с помощью метода моментов.
Этот
пример, разумеется, нельзя рассматривать как критерий
доказательства
преимуществ метода моментов в сравнении с при-
ближенным квантршьным методом оценивания статистических
характеристик эмпирических распределений частиц по размерам,
тем
более применительно к задачам генетического характера,
поскольку можно указать много других примеров, когда именно
квантильные меры оказывались наилучшими в отношении диагно-
стики обстановок осадконакопления по данным гранулометрии.
Он лишний раз демонстрирует методологическую несостоятель-
ность подхода к решению проблемы реконструкции обстановок
.
6 6
\
!
Асимметрия
7
Ф-единицы
Рис. 19. Эффект использования разных формул вычисления асимметрии
по данным гранулометрических анализов пляжных тт дюнных песков побе-
режья Новой
Зеландии
[380].
а
—
квантильная формула
Ф. П.
Шепарда
и Р.
Янга
[536];
б —
квантильная формула
Р.
Л.
Фолка
и В.
С.
Уарда
[402];
в —
формула
Г.
Фридмана [404], полученная
по
методу
моментов.
осадконакопления, которая реализуется, как правило, путем
перебора
статистических характеристик без предварительной (до
получения конечных результатов разделения обстановок накопле-
ния осадков) содержательной проработки проблемы, т. е. без
формулировки и интерпретации альтернативных гипотез, связы-
вающих
гилродинамические параметры среды с конечным распре-
делением частиц по фракциям.
Некоторые исследователи [439, 525] предлагают более строгие
методы
оценивания статистических характеристик фракционного
состава
пород, основанные на приближении эмпирической кривой
распределения частиц по фракциям полиномами Грам-Шарлье
[525]
либо на разлоячепии аппроксимирующей кривой распределе-
ния в ряд Эджворта
[439].
Следует отметить, что достигаемая
при этой точность не компенсируется вычислительными трудно-
стями при реализации этих методов на ЭВМ и требованиями к ко-
нечным результатам, которые прея^де всего долялны быть устой-
чивы в отношении различных методов оценивания. Поэтому прак-
тически и кваптильпый метод (средний размер зерен и стандартное
отклонение) и метод моментов (асимметрия и эксцесс) остаются
наиболее оптимальными приемами оценки статистических харак-
теристик распределения частиц по фракциям.

ЧИСЛЕННЫЕ
МЕРЫ СОРТИРОВКИ
Распределение частиц по фракциям принято характеризовать
особой мерой, которая получила название
«сортировка»
или
«фрак-
ционная
сортировка частиц». Иногда употребляется близкое по
смыслу понятие «однородность» осадка, которая также рассматри-
вается
в аспекте размеров слагающих осадок обломочных частиц.
Меры фракционной сортировки частиц доляшы учитывать харак-
тер распределения частиц по фракциям и фиксировать все фрак-
ции, в которых присутствует даже незначительное количество
частиц данной размерности. Кроме того, из смысла, вкладыва-
емого в понятие
«сортировка»
осадка, должна вытекать независи-
мость
численных мер, оценивающих сортировку, от вида распре-
деления
частиц в вероятностном смысле.
Рассмотрим с этих позиций наиболее распространенные в на
стоящее
время меры сортировки — коэффициент Траска [562]
и другие квантильиые оценки, а также стандартное отклонение
от
среднего размера частиц, которое почти всеми геологами интер-
претируется как мера сортировки осадка. Коэффициент сорти-
ровки Траска S
0
является
функцией
от двух квантилей (Q
25
и Q
75
)
и рассчитывается по формуле
г
Д
е
Q25 — 25%-ньтй квантиль, соответствующий зоне больших
размеров,
и Q
75
— 75%-пый квантиль, лежащий в диапазоне
частиц меньшей размерности.
Осадок считается идеально отсортированным, если Q
25
= Q
75
,
что возможно только в том случае, когда все частицы имеют
раз-
мер какой-то одной фракции. S
0
при этом равняется единице. Во
всех
остальных случаях S
0
>1. Коэффициент Траска ненорми-
рованная величина, изменяющаяся в широком диапазоне — от
первых
единиц
до первых десятков, что, естественно, затрудняет
построение удобной в практическом отношении классификации
осадков по степени сортировки.
Кроме
того, коэффициент Траска дает искаженную картину
сортировки, когда осадок сосредоточен в двух крайних,фракциях
либо в двух фракциях, разделенных несколькими фракциями,
не содержащими осадка. Действительно, на рис. 20 показаны 3 слу-
чая возмояшого распределения частиц по фракциям. В первом
(рис. 20, а) весь осадок сосредоточен в двух
крайних
фракциях
песчаной совокупности. Во втором (рис. 20, б) весь осадок рас-
пался также на две фракции, но ь диапазоне частиц крупнопесча-
ной размерности, к тому же разделенных единственной фракцией,
которая оказалась не представленной осадком. И, наконец, третий
случай (рис. 20, в) демонстрирует относительно равномерное
распределение частиц по фракциям. В первом случае осадок
предельно неоднороден, но относительно хорошо отсортирован;
(41)
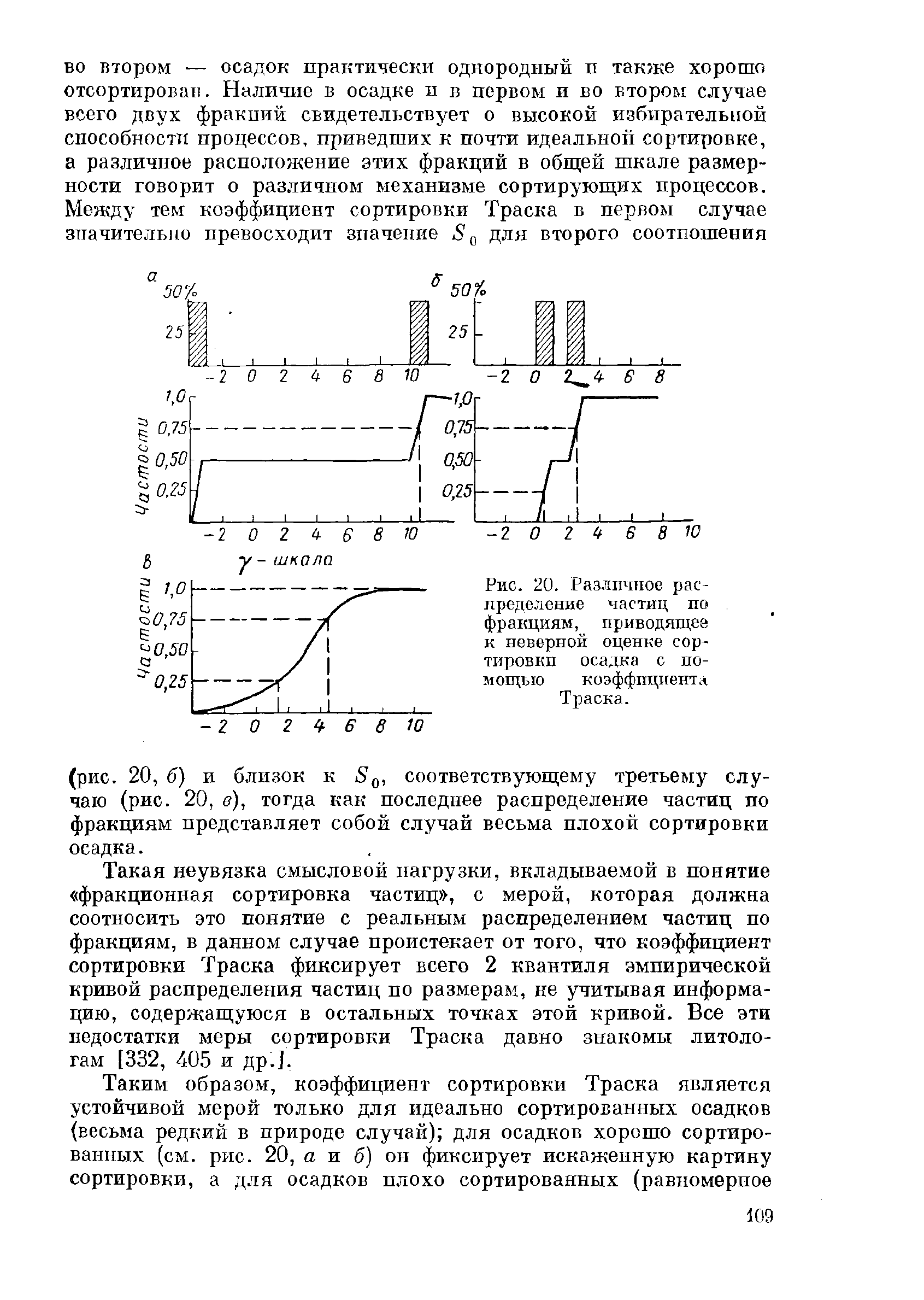
во
втором — осадок практически однородный п также хорошо
отсортировав.
Наличие
в осадке и в первом и во втором случае
всего
двух фракций свидетельствует о высокой избирательной
способности процессов, приведших к почти идеальной сортировке,
а
различное расположение этих фракций в общей шкале размер-
ности говорит о различном механизме сортирующих процессов.
Между тем коэффициент сортировки Траска в первом случае
значительно превосходит значение S
0
для второго соотношения
а
50%
25
-2
0 2 4-68
1
0,75
ь
1
50%
25
Ii
-2
0 2 4-68
у -
школа
8
Ю
Рис. 20. Различное рас-
пределение
частиц по
фракциям, приводящее
к неверной
оценке
сор-
тировки осадка с по-
мощью коэффициента
Траска.
-20
2468
W
(рис. 20, б) и близок к S
0
, соответствующему третьему слу-
чаю (рис. 20,
<?),
тогда как последнее распределение частиц по
фракциям представляет собой случай весьма плохой сортировки
осадка.
Такая неувязка смысловой нагрузки, вкладываемой в понятие
«фракционная сортировка частиц», с мерой, которая должна
соотносить это понятие с реальным распределением частиц по
фракциям, в данном случае проистекает от того, что коэффициент
сортировки Траска фиксирует всего 2 квантиля эмпирической
кривой распределения частиц по размерам, не учитывая информа-
цию, содержащуюся в остальных точках этой кривой. Все эти
недостатки меры сортировки Траска давно знакомы литоло-
гам
[332, 405 и др.].
Таким образом, коэффициент сортировки Траска является
устойчивой мерой только для идеально сортированных осадков
(весьма
редкий
в природе случай); для осадков хорошо сортиро-
ванных (см. рис. 20, а и б) он фиксирует искаженную картину
сортировки, а для осадков плохо сортированных (равномерное

распределение частиц по фракциям) он может рассматриваться
в
качестве грубой
оценки
сортировки частиц по фракциям.
Приведенные нами примеры (см. рис. 20), для которых коэф-
фициент Траска не только приближенно характеризует сорти-
ровку осадка, как это считалось ранее, а даже иская^ает картину,
наводит на мысль о том, что от коэффициента Траска лучше отка-
заться
совсем, тем более что существуют меры сортировки, ли-
шенные всех этих недостатков. Помимо меры сортировки, пред-
ложенной П. Траском, неоднократно вводились и другие меры,
основанные как на квантильных, так и на момеитных оценках.
Все
они так или иначе фиксировали совпадение стандартного
отклонения от среднего а, как
численной
меры, с понятием
«фрак-
ционная
сортировка частиц», которое отражается этой мерой.
Ряд этих характеристик приведен нами в табл. 4 (меры сорти-
ровки Д. JI. Инман а, Р. Л. Фолка и В. С. Уарда, Р. Б. Маккэм-
мона).
Причем все они исходят из предположения о логарифми-
чески-нормальном распределении размеров частиц и соответ-
ственно из унимодальности этой кривой распределения.
Г.
М. Фридман [405] на материале 612 образцов песчаников
и песков рассчитал сортировку с помощью квантильных мер,
предложенных разными авторами, и стандартного отклонения,
сосчитанного по методу моментов. Оказалось, что все они прак-
тически
идентичны
друг другу (за исключением коэффициента
Траска).
Так, коэффициент
корреляции
г между сортировкой
по Д. Л. Инману и стандартным отклонением равен 0,99; менаду
сортировкой по Р. Л. Фолку и В. С. Уарду истандартньщ отклоне-
нием — 0,98; между сортировкой по Р. Л. Фолку и В. С. Уарду
и сортировкой по Д. Л. Инману — 0,96. Однако численное совпа-
дение
всех этих мер еще не означает, что все они столь я^е аде-
кватны самому понятию
«сортировка»,
которое они призваны отра-
я^ать.
Следует заметить, что всем квантилышм и моментпым мерам
сортировки в
принципе
может быть придай «реальный» смысл
только для унимодальных ,кривых, для которых определены
статистические приемы
оценки
значимости стандартного отклоне-
ния от среднего. Для бимодальных, а тем более полимодальных
кривых все численные
оценки
стандартного отклонения (сорти-
ровки),
которые мы приводили, оказываются весьма грубыми
и в этом смысле практически неприемлемыми. С переходом же на
дробные гранулометрические анализы, когда анализируется весь
диапазон размерностей, включая песчаную, алевритовую и гли-
нистые совокупности,
наличие
дефицитов на рубея\е этих совокуп-
ностей предопределяет появление локальных минимумов кривой
распределения и как следствие этого би- или полимодальность
этой кривой. Унимодальные распределения при дробных ситовых
анализах составляют редкое исключение, а потому и меры сорти-
ровки, которые мы обсуячдали, остаются справедливыми только
для узких
популяций
частиц, распределение которых характери-
