Розанов Н.Н. Нелинейная оптика. Часть I. Уравнения распространения излучения и нелинейный отклик среды
Подождите немного. Документ загружается.


где
33 3 3
2
33
(, 1,2)
lm l m
ml
ml
ε
εεε
α
ε
−
==. (1.6.8)
Для среды с пренебрежимо слабой анизотропией первый член в левой
части (7) отсутствует, а во втором члене
ml ml
α
δ
=
, так что в этом случае
приходим к (1.5.19).
Ввиду анизотропии среды изменения возникают и в описывающем
частотную дисперсию 3-м члене (1). Дисперсия определяется заданием
фурье-разложений поля и электрической индукции (знак вещественной
части опускается):
00
()
00
exp( ) exp[ ( ) ] ,
ˆ
exp( ) ( ) exp[ ( ) ] .
l
ik z i t d
ik z i t d
δω
δω
ωδω δω
ε
δω ω δω δω
=−+
=−
∫
∫
EE
DE
+
(1.6.9)
Теперь
2()
2
00
22
1
ˆ
exp( ) ( ) exp[ ( ) ]
l
ik z i t d
ct
δω
δ
ωωδω
∂
−= −+
∂
∫
D
kE
δω
, (1.6.10)
где введен тензор
2
2
0
2
()
ˆ
ˆ
() (
c
ωδω
)
δ
ω
+
=k
εδω
. (1.6.11)
Разложение Тейлора этого тензора записывается в виде
2
2()()
0
0
ˆ
1
ˆˆ
ˆ
() (),
!(
n
nnn
n
n
d
nd
δω
δω δω
δω
∞
=
)
=
==
∑
k
kQQ . (1.6.12)
В частности,
представляет тензор обратной групповой скорости, а
– тензор квадратичной дисперсии. Теперь (10) примет вид
(1)
ˆ
Q
(2)
ˆ
Q
2()
()
00
22
0
1
ˆ
exp( )
!
lnn
N
n
n
n
i
ik z i t
ct n t
ω
=
∂∂
−= −
∂∂
∑
DE
Q
, (1.6.13)
где целое число N указывает порядок теории дисперсии. В правой части
(13) присутствуют продольные компоненты векторов
. Их можно выразить через поперечные
компоненты этих же векторов, продифференцировав (7) j раз по времени:
()
/ ( 0,1, 2,...)
jj j
tj=∂ ∂ =VE
()
22
() ()
33
1,1
33 0
1
j
jj
m
mm ml
mml
m
V
i
VV
kx
εα
ε
==
∂
=− +
∂
∑∑
. (1.6.14)
Тогда для поперечных компонент вектора
найдем (p = 1, 2)
() ()
ˆ
n
QV
j
()
22
3
() () () () () ()
33
1,
33 0
ˆ
()
1
j
q
nj n n j n
m
ppqpqpmn
qm
n
V
i
QQVQ
kx
ε
α
ε
==
⎛⎞
∂
=− +
⎜⎟
n
∂
⎝⎠
∑∑
QV
. (1.6.15)
Применяя эти соотношения к (13), получим
21
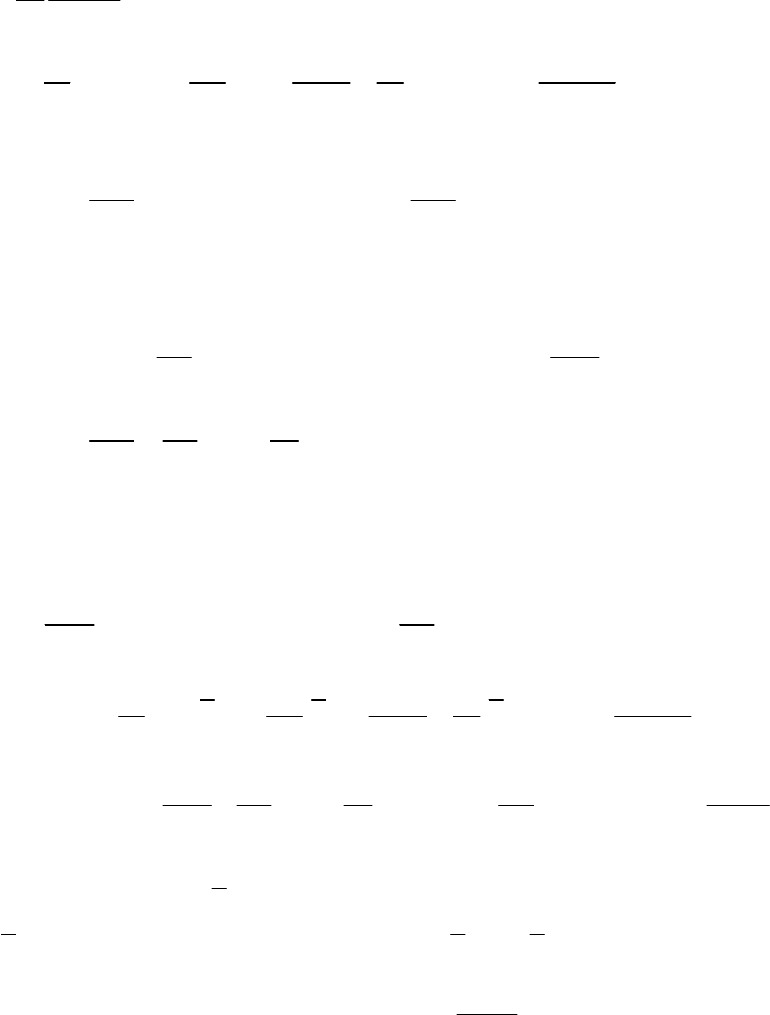
2()
00
22
1
2
3
() () ()
33
01 ,1
33 0
1
exp( )
.
!
l
p
n
n
n
N
qq
nn n
m
pq p p mj
nn
nq mj
j
D
ik z i t
ct
E
2
E
ii
QQ Q
ntk
ω
ε
α
ε
+
== =
∂
−=−×
∂
∂
⎛⎞
∂
×− +
⎜⎟
∂∂
⎝⎠
∑∑ ∑
xt
∂
(1.6.16)
Последний член левой части (1) имеет вид
0
grad grad grad exp( )
zz
z
EE
ik E ik z i t
zz
00
ω
⊥⊥⊥
∂∂
⎛⎞
−=− + −
⎜⎟
∂∂
⎝⎠
. (1.6.17)
После подстановки сюда (7) и введения двумерного вектора
3313
(,
2
)
ε
ε
⊥
=ε
найдем
2
0
03
,1
33
grad grad ( , ) grad
m
zm
mj
j
kE
ik E i
j
x
α
ε
⊥⊥⊥⊥⊥
=
⎛⎞
∂
=+
⎜
⎜
∂
⎝⎠
∑
ε E
⎟
⎟
, (1.6.18)
3
33
1
grad grad ( , )
z
E
zz
ε
⊥⊥
∂∂
−=
∂∂
ε E
⊥⊥
. (1.6.19)
В последнем выражении мы пренебрегли членом
22
0
~( ) ( / )kr E r
−
⊥
⊥⊥
.
Суммируя полученные выражения, мы получаем окончательно
квазиоптическое уравнение с поправочными членами:
0
03
33
1
22 2
3
() () ()
33
10 1 ,1
33 0
2
2
30
2
,1
33
2 grad div grad ( , )
!
14
grad grad ( , ) 2
n
n
n
N
qq
nn n
m
ppqp pmj
nn
pn q mj
j
m
mj
mj
j
k
ik i
z
E
E
ii
QQ Q
ntkxt
E
i
xzc
ε
ε
α
ε
π
αωδ
ε
⊥
⊥⊥ ⊥ ⊥⊥ ⊥ ⊥ ⊥
+
== = =
⊥⊥⊥⊥⊥
=
∂
+∆ − + +
∂
⎡⎤
∂
⎛⎞
∂
+−+ +
⎢⎥
⎜⎟
∂∂∂
⎢⎥
⎝⎠
⎣⎦
∂
∂
++ ++
∂∂
∑∑ ∑ ∑
∑
E
EE ε E
e
ε EP
2
0
0.
t
δ
ω
⊥
∂
⎛⎞
=
⎜⎟
∂
⎝⎠
P
(1.6.20)
Коэффициенты
()n
p
q
Q
совпадают с
()n
p
q
Q
при 0, 2n
≠
, при этом
(0) (0) 2
0
p
qpq
QQk
pq
δ
=−
, а различие между
(2)
p
q
Q
и
(2)
p
q
Q
связано с обсуждавшимся
в предыдущем разделе вкладом члена
2
2
z
⊥
∂
∂
E
, см. (1.5.24).
Уравнение (20) описывает, в частности, перемешивание поперечных
компонент огибающей вследствие анизотропии среды. Для изотропной
среды (20) сводится к (1.5.18).
1.7. Квазиоптическое уравнение для метаматериалов
Для естественных сред в оптической области магнитная
проницаемость µ близка к единице, и это условие до сих пор мы считали
выполненным. В последнее время развиваются технологии создания
искусственных сред с произвольными значениями эффективной
22

магнитной проницаемости, в том числе отрицательными. В этом разделе
мы выведем квазиоптическое уравнение, описывающее распространение
монохроматического излучения в изотропном метаматериале с
нелинейными диэлектрической проницаемостью ε и магнитной
восприимчивостью µ:
22
00
22
0
00
(| | ), (| | ),
|(||)|||,|(||)|| |,
Im Im 0.
εε δε µµ δµ
δε ε δµ µ
εµ
=+ =+
==
EH
EH
0
H
(1.7.1)
Будем исходить из уравнений Максвелла для монохроматического
излучения с частотой ω (комплексная форма записи):
rot , rotic i c
ωµ ωε
==−HEE
. (1.7.2)
Отсюда можно выразить
через (с учетом зависимости ,
строго говоря, определение этой зависимости сводится к решению
трансцендентного уравнения):
H
E
2
(| | )
δµ
H
rot
c
i
ωµ
=−H
E
. (1.7.3)
С учетом этого соотношения получаем замкнутое уравнение для
напряженности электрического поля
2
2
1
rot rot
c
ω
ε
µ
⎛⎞
=
⎜⎟
⎝⎠
E
E
, (1.7.4)
или
22
22
1
graddiv [grad rot ] 0
zc
ω
εµ µ
µ
⊥
⎛⎞
∂
+∆ + − − × =
⎜⎟
∂
⎝⎠
EE E E E
. (1.7.5)
В невозмущенной прозрачной линейной среде (
0
δ
εδµ
=
=
) решение
имеет вид плоской волны с зависимостью напряженностей поля от z (в
комплексной форме записи) вида exp(ikz), где волновое число
00
k
c
ω
ε
µ
= ,
причем считается
00
0
ε
µ
>
(в противном случае распространение волны
невозможно). Существенно, что напряженности электрического и
магнитного поля связаны соотношениями
0
00
[],
z
ε
µµ
=× =HeEH
0
ε
E
. (1.7.6)
Для вывода квазиоптического уравнения полагаем
Re{ exp( )}, Re{ exp( )}ikz ikz==
EE HH
. (1.7.7)
В стандартных для квазиоптики приближениях получаем искомое
уравнение в виде
23
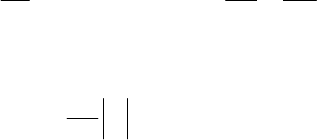
2
00
2ik k
z
δε δµ
εµ
⊥⊥⊥ ⊥
⎛⎞
∂
+∆ + + =
⎜⎟
∂
⎝⎠
EE E
0
. (1.7.8)
При этом без потери точности можно считать
2
0
0
ε
δµ δµ
µ
⎛⎞
=
⎜
⎝⎠
E
⎟
−
. (1.7.9)
Замечание. Подход работы N. Lazarides, G.P. Tsironis. Phys. Rev. E.
Vol. 71. 036614 (2005), в которой вводятся связанные квазиоптические
уравнения для напряженностей электрического и магнитного полей,
некорректен.
1.8. Приближение слабой непараксиальности
Хотя квазиоптический подход чрезвычайно плодотворен и позволяет
решить большое число нелинейной оптики, область его применимости
ограничена пучками сравнительно большой ширины (в единицах длины
волны) и импульсами достаточно большой длительности (в единицах
периода оптических колебаний). В то же время в ряде ситуаций такое
предположение неприемлемо. Например, для сред с керровской
самофокусировочной нелинейностью
(см. гл. 2) квазиоптический подход
описывает так называемый коллапс пучка с мощностью, превышающей
критическую. При приближении к точке нелинейного фокуса
максимальная интенсивность излучения стремится к бесконечности, а
ширина пучка – к нулю. Понятно, что последнее обстоятельство нарушает
условия применимости квазиоптического подхода и требует уточнения
рассмотрения.
Непосредственное решение нелинейных уравнений Максвелла
затруднительно и
на сегодня практически возможно лишь для одномерной
или двумерной геометрии (следующая часть Пособия). В данном разделе
мы представим вывод более точного, чем квазиоптическое, уравнения
распространения широких пучков монохроматического излучения в среде
с кубичной нелинейностью, причем непараксиальные члены служат малой
поправкой к основным параксиальным [18].
Вывод близок к представленному выше в разделах 1.5-1.7, но
теперь
мы учтем некоторые дополнительные члены. Исходим из тех же
уравнений Максвелла и пренебрегаем для простоты частотной дисперсией.
Среда вновь считается изотропной и немагнитной (µ = 1). Положим вместо
(1.5.5)
0
Re{ ( , )exp( )}zizit
ω
⊥
=ΓEEr
. (1.8.1)
Сдвиг постоянной распространения (Г вместо
) удобен, например, для
описания пространственных солитонов (следующая часть Пособия) с
огибающей , которая зависит только от поперечных координат
0
k
()
s ⊥
Er
24

(, )
x
y
⊥
=r
. Теперь точным следствием волнового уравнения служит
соотношение
22
22
0
0
22
2 ( ) grad div 0
k
ik
zz c
δ
⊥⊥
⊥⊥ ⊥ ⊥
∂∂
Γ+ +∆−Γ− + − =
∂∂
EE
EEDE
)
. (1.8.2)
Это уравнение незамкнуто относительно поперечных составляющих
огибающей (,
x
y
E
E
⊥
=E из-за формы последнего члена в левой части (2).
Как и ранее, замкнутое уравнение может быть получено при
использовании приближенного выражения для продольной компоненты
z
E
через вида (1.5.19). Тогда, пренебрегая членами высшего порядка
по малому параметру непараксиальности
⊥
E
2
0
()kr
−
⊥
, находим
2
22
0
0
2
2()
k
ik
zc
δ
⊥
⊥⊥ ⊥ ⊥ ⊥
∂
Γ+∆−Γ− + =
∂
E
EEDQ
. (1.8.3)
Правая часть (3) представляет малую непараксиальную поправку вида
s
z⊥
=+QQQ
, причем в случае кубичной нелинейности среды вида (см.
гл. 2)
*
(, ) (,)
δα β
=+DEEEEE
*
E (1.8.4)
получим
22*
0
22*
22
1
{|div | (div )
grad [div ( | | )]
grad [| | (div )] grad ( div )},
s
EE
EE
αβ
ε
αβ
αβ
⊥⊥ ⊥ ⊥⊥ ⊥
⊥⊥ ⊥⊥ ⊥⊥
⊥ ⊥ ⊥⊥ ⊥ ⊥ ⊥⊥
=− − +
++−
−+
QEEEE
EE
EE
*
()
2
2
22 2
0
0
22
00
2
22 2 2*
0
0
0
**
0
1
()||
() ||
[( , ) ( , )]
4
z
k
kE
zk
k
kEE
α
ε
αβ
ε
α
ε
⊥
⊥⊥
⊥⊥ ⊥ ⊥ ⊥ ⊥⊥
⊥⊥ ⊥ ⊥⊥ ⊥ ⊥
⎡⎤
∂
=− = ∆ − Γ − + ×
⎢⎥
∂
⎣⎦
⎡⎤
×∆ −Γ− + + +
⎢⎥
⎣⎦
+∆ −∆ +
E
Q
EE EE
EE EE E
*2* 222*
0
0
22
22* 4
00
00
[2( , ) ( )
4
(2)|| || ].
EkE
kk
EE E
β
ε
αβ β
εε
⊥⊥ ⊥ ⊥ ⊥⊥⊥ ⊥⊥
⊥⊥⊥ ⊥⊥
+∆ −∆−Γ−
++ −
EEE E E
EE
+
(1.8.5)
В низшем (параксиальном, или квазиоптическом) приближении
правая часть (3) обращается в нуль,
0
⊥
=
Q
, и тогда (3) сводится к
варианту (1.5.18) для монохроматического излучения. Можно сказать, что
параксиальный подход реализуется как предел при стремлении ширины
пучка к бесконечности. В отличие от исходного волнового уравнения это
25
уравнение эволюционного типа с первой производной по z. Поэтому оно
позволяет находить огибающую поля в любом сечении z, если она задана в
исходном сечении z = 0. Одним из следствий непараксиальности служит
повышение степени нелинейности. Так, если, как это принято в (4),
δ
D –
3-го порядка по огибающей, то
⊥
Q
содержит и члены 5-го порядка.
Естественно, что их учет обоснован, если коэффициенты членов 5-го
порядка в самой нелинейности
δ
D достаточно малы. Учет
непараксиальных эффектов принципиально важен в пограничных
(вырожденных) ситуациях, когда даже малые поправки могут качественно
изменять характер результата (например, устранение коллапса при
самофокусировке в среде с керровской нелинейностью, см. следующую
часть Пособия). Также в следующей части Пособия будут обсуждены
особенности эволюционных уравнений в случае предельно коротких
оптических
импульсов.
Литература к главе 1
1. S.I. Wawilow, W.L. Lewschin. Z. Physik. 1926. № 35. P. 932.
2. Л.Д. Ландау, Е.М. Лифшиц. Электродинамика сплошных сред. М.,
Физматлит, 1982.
3. C. Cohen-Tannoudji, A. Kastler. Progress in Optics. 1966. Vol. 5. P. 1.
4. P. Franken, A. Hill, C. Peters, G. Weinreich. Phys. Rev. Lett. 1961. V. 7. № 3.
P. 118.
5. Е.Б. Александров, А.А. Ансельм, А.Н. Москалев. ЖЭТФ. 1985. Т. 89.
С. 1181.
6. Н.Н. Розанов. ЖЭТФ. 1993. Т. 103. № 6. С. 1996.
7. Н.Н. Розанов. ЖЭТФ. 1998. Т. 113. № 2. С. 513.
8. N.N. Rosanov. Phys. Vibration. 1999. Vol. 7.
№ 1. P. 28.
9. В.Б. Берестецкий, Е.М. Лифшиц, Л.П. Питаевский. Квантовая
электродинамика. М., Наука, 1989.
10. Л.Д. Ландау, Е.М. Лифшиц. Квантовая механика. Нерелятивистская
теория. М., Наука, 1989.
11. В.И. Денисов. Введение в электродинамику материальных сред. М.,
МГУ, 1989.
12. И.Р. Шен. Принципы нелинейной оптики. М., Физматлит, 1989.
13. Н.Н. Розанов, В.
А. Смирнов. Опт. спектроск. 2004. Т. 97. № 4. С. 638.
14. М.А. Леонтович. Изв. АН СССР. Сер. физ. 1944. Т. 8. № 1. С. 16.
15. М.А. Леонтович, В.А. Фок. ЖЭТФ. 1946. Т. 16. № 7. С. 557.
16. Л.Д. Ландау, Е.М. Лифшиц. Теория поля. М., Физматлит. 1960.
17. Ф.Б. Васильева, В.Ф. Бутузов. Асимптотические разложения решений
сингулярно возмущенных
уравнений. М., Наука, 1973.
18. N.N. Rosanov. Spatial hysteresis and optical patterns. Springer, Berlin, 2002.
26
Глава 2. МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
Для замыкания приведенных в гл. 1 уравнений распространения
излучения необходимо еще конкретизировать материальные уравнения,
описывающие линейные и нелинейные оптические свойства среды и ее
взаимодействие с излучением. Идеальным было бы задание
квантовомеханического уравнения Шредингера или матрицы плотности
(см. ниже п. 2.3) для составляющих среду элементов – электронов, ядер и
ионов, – но
такой путь на сегодня, как правило, нереалистичен из-за
чрезвычайной сложности решения этих уравнений. Поэтому здесь
рассматриваются два подхода. Первый связан с упрощенными моделями
среды, включая классическую модель Друде – Лоренца (п. 2.1) и
квантовомеханические модели (п. 2.2 – 2.4). Второй подход основан на
макроскопических моделях (п. 2.5) и феноменологическом описании
(п. 2.6). В заключении приведен вид
нелинейных уравнений Максвелла,
включающих материальные соотношения, для электрон-позитронного
вакуума (п. 2.7); актуальность этого вопроса связана с прогрессом в
получении высоких интенсивностей лазерного излучения.
2.1. Классические модели среды
Классические модели имеют ограниченную область применимости;
в частности, отличие магнитной проницаемости естественных сред от
единицы последовательно объясняет только квантовая теория. Однако они
просты и
по крайней мере качественно описывают многие аспекты
линейного и нелинейного отклика среды на оптическое излучение.
В основной классической модели Друде – Лоренца (п. 2.1.1 и 2.1.2)
среда представляется набором осцилляторов (молекул или, в случае
искусственных метаматериалов, более сложных «элементарных блоков»).
Наводимый излучением дипольный момент одного осциллятора
,
где 0 – заряд электрона и
– смещение электрона от положения
равновесия. Поляризованность
для одинаковых молекул с
концентрацией
, или
e=−dr
e−<
r
0
N=P
d
0
N
ii
i
N=
∑
Pd
для различающихся молекул.
Концентрация молекул считается малой (нет диполь-дипольного
взаимодействия, например, разреженный газ, поэтому можно не учитывать
различия между локальным и действующим полем, см. ниже п. 2.3.3 и
2.4.4). Другие классические модели (п. 2.1.3 и 2.1.4) отвечают как
молекулярным моделям среды (в том числе состоящей из анизотропных
молекул с собственным дипольным моментом),так
и метаматериалам, в
которых «элементарная ячейка» состоит из столь большого числа молекул,
что может рассматриваться классически.
27
2.1.1. Линейная модель Друде – Лоренца
Уравнение движения одного линейного (гармонического)
осциллятора является конкретизацией второго закона Ньютона:
2
0
mmm e
γω
=− − −rrr
E. (2.1.1)
Здесь m – масса электрона,
0
ω
– резонансная частота колебаний
(линейный закон Гука), γ – коэффициент трения, пропорционального
скорости (
0
0
γ
ω
<
). Скорость движения электрона много меньше
скорости света, поэтому в силе Лоренца (1.2.33), с которой
электромагнитное поле действует на электрон, достаточно сохранить
только член
, пренебрегая воздействием магнитного поля (последнее
проявляется в возникновении слабой квадратичной нелинейности [1]).
Смещения электрона порядка размера атома или молекулы (
см), что
много меньше длины волны оптического излучения (
см). Поэтому
напряженность электрического поля
не зависит от координаты. Если
среда состоит из одинаковых осцилляторов с концентрацией
(однородное уширение), то из (1) находим материальное соотношение в
виде ( – поляризованность, точки сверху означают
дифференцирование по времени):
eE
8
~10
−
5
~10
−
E
0
N
0
Ne=−P
r
2
2
0
4
p
ω
γω
π
++ =PP P
E
, (2.1.2)
где введена плазменная частота
p
ω
соотношением
2
2
0
4
p
Ne
m
π
ω
=
. (2.1.3)
Для излучения с фиксированной (линейной) поляризацией достаточно
рассмотреть скалярное уравнение
2
2
0
4
p
PP P
ω
γω
E
π
++ =
0
. (2.1.4)
Если среда состоит из набора осцилляторов с различающимися
параметрами, например, резонансной частотой, то выражение для
поляризации среды описывается интегралом
00
()()PgPd
ω
ωω
+∞
−∞
=
∫
, (2.1.5)
где введена весовая функция
0
(g )
ω
. Это уравнение представляет один из
простейших вариантов материального уравнения для сплошных сред.
Феноменологическая модель согласуется с последовательной
квантовомеханической (см. ниже п. 2.2–2.4) в тех ситуациях, когда
существенное значение имеет только один резонанс в среде, отвечающий
28
электродипольному переходу. Если положить в (4)
0
0
ω
=
, то это
уравнение будет описывать оптические свойства плазмы (модель Друде).
Модель (4) обычно используется в рамках спектрального подхода,
оправданного ввиду линейности задачи. Поле излучения разлагается в
спектр монохроматических волн с помощью интеграла Фурье
*
1
( ) exp( ) , ( ) exp( ) ,
2
E
tEitdE Et itdtEE
ωω
ω
ωω
ωω ω
π
++
−
−∞ −∞
==−
∫∫
ω
=
. (2.1.6)
Аналогичным образом раскладывается поляризованность среды
() exp( )Pt P i t d
ω
ω
ω
ω
+
−∞
=
∫
. (2.1.7)
Линейную восприимчивость среды
(1)
()
χ
ω
, определяемую соотношением
(1)
()PE
ω
ω
χω
= , (2.1.8)
находим подстановкой (6) и (7) в (4):
2
(1) 2 2
0
() , ()
4()
p
Di
D
ω
χ
ωωω
πω
==−
γωω
−
. (2.1.9)
Два простых нуля знаменателя последней дроби
ω
±
располагаются в
нижней полуплоскости комплексной переменной ω:
2
2
00 0
,
24
i
γ
γ
ωωωω
±
=− ± = −
. (2.1.10)
Этот вывод имеет общий характер, не ограниченный рассматриваемой
моделью термодинамически равновесной среды, и отвечает принципу
причинности. Из последнего, в свою очередь, вытекают соотношения
Крамерса – Кронига [2] между вещественной и мнимой частями линейной
восприимчивости. Так как ввиду (9) и (3) восприимчивость
пропорциональна концентрации осцилляторов
, то можно ввести не
зависящую от концентрации поляризуемость осциллятора
0
N
2
(1) (1)
0
1
() ()
()
e
Nm
αω χω
D
ω
==
. (2.1.11)
Поляризуемость характеризует отклик на излучение одиночного
осциллятора.
Ввиду слабости затухания (
0
γ
ω
) описываемый (9) отклик среды
обладает резким резонансом при
0
ω
ω
≈
, причем ширина резонанса
. Комплексность восприимчивости, существенная вблизи
резонанса, отвечает сдвигу фазы колебаний поляризованности по
отношению к колебаниям поля. С другой стороны, это обстоятельство
означает комплексность линейной диэлектрической проницаемости
9-1
~~10c
γ
2
(1) (1)
() 1 4 () 1
()
p
D
ω
εω πχω
ω
=+ =+
, (2.1.12)
29

то есть наличие частотной дисперсии у показателя преломления и
коэффициента поглощения.
Задание восприимчивости среды не полностью эквивалентно
заданию динамического материального уравнения (4). Действительно, для
решения последнего нужно еще фиксировать начальные условия,
отсутствующие в выражении (9). Фактически при переходе от (4) к (9)
было учтено только установившееся решение (4) и игнорировалось
свободное решение (4) (при 0
E
=
), которое экспоненциально, со
скоростью γ, затухает от некоторого исходного начального значения.
Ввиду линейности задачи знание восприимчивости (8) позволяет
описать и отклик среды на импульс излучения произвольной формы. При
этом начальные условия отвечают тому, что до падения импульса
осцилляторы неподвижны. Заметим, что даже в случае коротких
импульсов возбуждающего излучения затухание имеет принципиальное
значение. Если пренебречь им, то после прохождения импульса
осцилляторы колебались бы неограниченно долго и, соответственно,
испускали в виде излучения бесконечную энергию.
Как мы видели, линейность задачи не означает, что излучение не
меняет состояния среды. Напротив, излучение приводит к раскачке
осцилляторов среды, наиболее выраженной вблизи резонансных частот.
На отклик среды накладывается
лишь требование его малости
(линейности). В рамках данной модели полезно рассмотреть следующую
задачу [3]. Пусть из вакуума на границу среды, моделируемой набором
линейных осцилляторов, падают два коротких импульса, разделенные
временным интервалом
1
τ
γ
−
<
. Первый импульс вызывает в среде
осцилляции и потому меняет условия прохождения и отражения второго
импульса. Оказывается, что при определенных условиях второй импульс
не отражается от границы среды, хотя в отсутствие первого импульса
имеет место обычное френелевское отражение. Однако, такой эффект не
означает подлинного нелинейного взаимодействия импульсов. Его
природа – интерференционная и
отвечает взаимному гашению
отраженного излучения второго импульса и излучения осцилляторов,
продолжающегося в течение времени
1
~
γ
−
.
2.1.2. Осцилляторы с квадратичной и кубичной нелинейностью
Теперь среда моделируется ангармоническими осцилляторами, так
что «возвращающая сила» отвечает нелинейному закону Гука (сила не
пропорциональна растяжению пружины, а содержит нелинейную
составляющую). Считая нелинейность слабой, обобщим (4)
2
223
02 3
...
4
p
PP P P P
ω
γω κ κ
E
π
++ + + +=
. (2.1.13)
Слабость нелинейности отвечает условиям
30
