Савельвев А.Я. Основы информатики

Подождите немного. Документ загружается.

6 I Методы деления двоичных чисел

В общем случае «школьный» алгоритм деления на примере двоичных

чисел выглядит следующим образом:

1100100 IIOIO —делитель

1010

делимое —

делитель —

остаток —

1010 -—частное

0101

1010

воссчаиовление остатка -

1011

1010

01010

1010

0000

Здесь цифры частпою получаются последовательно, начиная со стар-

шего разряда иугем вычитания делителя из полученного остатка. Ксли по-

лучен Гюложигельный остаиж, то цифра частного равна единице; если ос-

таток очрнцательный, го цифра частного равна нулю, при этом

восстанавливается предыдущий положительный остаток.

В случае ноложите;гьного остатка для гюлучения следующей цифры

частого 1юсле/(ннй остаток сдвигается влево на один разряд (либо дели-

мгпъ и11[);1во па один разряд) и из него вычитается делитель и т. д.

И cjiy4ae отрицателыюго остатка восстанавливается предыдущий тю-

JK)жиleJи>ilЫH ociaTOK прибавлением к отрицательному остатку делителя, и

В(юс1аиовлеппый остаюк сдвигается на один разряд влево (либо сдвигается

дcJrпieJи. вправо па один разряд) и из него вычитается делитель. Такой ал-

inpniM деления получил название алгоритма деления с восстановлением

осинка. <|)ормально все действия можно описать следующим образом.

Пусп. А делимое, В — делитель и С — частное, при этом

А =0, а^а^

"•(•'„'-

В -О, h^2 •••b„,C - О, CjC^ ...с„.

Для реализации алгоритма деления двоичных чисел, представленных в

(|)орме с ((шксированной занятой, необходимо, чтобы выполнялось условие

\yi\

[Я[. IxjHi ло условие не выполпяегся, ю в первом шаге возникает пе-

peiHunienne разрядной сетки и операция не выполняется. Если Ы<|5|, то

иц первом maie операции проводится сдвиг делителя и определяется оста-

ток А^=- А -В'2 '.

Пусть /J| >0, тогда С, = I . Процесс деления продолжается дальше:

Ау^А^-В-2 ^

141

6 Выполнение операций деления чисел на двоичных сумматорах

Пусть А<0, тогда С^ =

и проводится восстановление остатка /(,:

Aj -Д

^В-Т'-.

Эгот остаток принимается за A'j и деление продолжается дальше сле-

дующим образом: А^ - A'j- В- 2"^.

Таким образом, алгоритм деления можно описать в общем виде на 7-м

шаге:

4 =4_i-fi-2"'. (6.1)

Ecjm Д >0, то С,=] и переход к следующему шагу; если Д <0, то

С\ ^

и восстановление остатка

Д_1 =А,^-В-2-',

(6.2)

который принимается за остаток А], и процесс продолжается но формуле

(6.1).

Следовате;гьно, операция деления сводится к носледовачельпому вы-

полнению вычитании (сложений) в сумматоре и сдвигам делителя. Сдви|-

дeJПJтeля может быть заменен сдвигом содержимого сумматора в противо-

положную сторону.

Алгоритм деления, основанный на реализации формул (6.1) и (6.2), на-

зывается делением с восстановлением остатка.

Рассмотрим процесс восстановления остатка. -4, <

н С, ={), то fia

следующем шаге выполняются действия по формуле А,^^ - ,4^'- Л-2"''*'* =

А^

+ В-2~'

-5-2^''*".

После преобразования получим

<1 =4+fi-2""^". (6.3)

Таким образом, появляется возможность построить алгоритм деления

по следующей схеме: Д - Д_| - fi

•

2"^',

если Д

О, то С, = I и переход к

следующему шагу; если Д<0, то С, =

и продолжение по формуле

Д^1 - Д + fi- 2 '"^'*. При этом, если Д^, >

, то С,^|

=: I

н переходим к фор-

муле (6.1), если Д^, <0, то C^^i -О и переходим к формуле (6.3). Такой

алгоритм называется делением без восстановления остатков.

Реализация рассмотренных алгоритмов деления возможна с гюмощью

двоичных сумматоров обратного или дополнителыюго кода. /1^ля хранения

дели1еля, де1Н1Мого и накопления очередных разрядов частного выдсля101ся

регистры. Минимальный состав блоков, необходимый для вьиюлиения де-

лений, показан на рис. 6Л в двух вариантах. Варианты отличаются сгюсо-

142

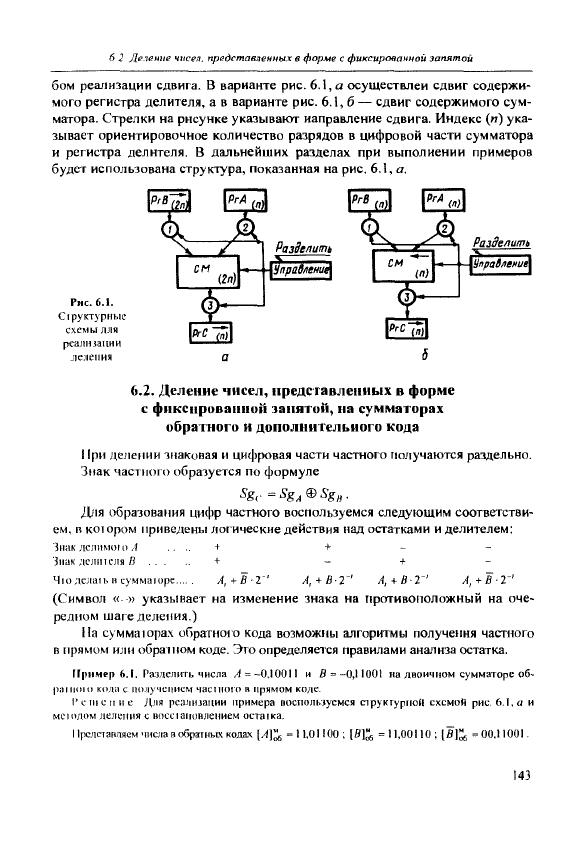
6 2 Де-ь

? чисел, представленных в форме с фиксированной запятой

бом решшзации сдвига. В варианте рис. 6.1, а осуществлен сдвиг содержи-

мого регистра делителя, а в варианте рис. 6.1, б — сдвиг содержимого сум-

матора. Стрелки на рисунке указывают направление сдвига. Индекс (и) ука-

зывает ориентировочное количество разрядов в цифровой части сумматора

и регистра делителя. В дальнейших разделах при выполнении примеров

будет использована структура, показанная на рис. 6.1, а.

Рис.

6.1.

CrpyKTvpfrbie

схемы ляя

реализации

6.2. Деление чисел, представленных в форме

с фиксированной запятой, на сумматорах

обратного и дополнительного кода

i !ри делении знаковая и цифровая части частного получаются раздельно.

Знак част1гого образуется по формуле

1Ь\я образования цифр частного воспользуемся следующим соответстви-

ем,

котором приведены логические действия над остатками и делителем:

Знак делимого/) , . .. + +

'Знак делителя Й + - +

Чю ;ie;iafb » ey\fMaiope /J, + В -2"' А, + В-2~' А,

В-2~' А,

В -2'

(Символ « » указывает на изменение знака на противоположный на оче-

редном шаге деления.)

Иа суммаюрах обратною кода возможны алгоритмы получения частного

в прямом ш\и обратном коде. Это определяется правилами анализа остатка.

[[ример 6.1. Разделить числа А

-UJOOI \ и В

-0,11001 на двоичном сумматоре об'

рапиио коли с получением частого в прямом коде-

Ре m с и и е }[пя реализации примера воспользуемся с1рукгурпоИ схемой рис, 6.1, а и

меюдом деления с воссюповлеиием остатка,

11релстапляемчиславобрагнычкодах

l^l^ls

=11,01100; [В]'^ =11,00110; [В]'^ =00.11001.

из

б Иылолнеипе onepatiiiii деления чисел

на

двоичных сулшаторал

Определим знак частного:

Sg,• ^

Sg^

®Sg/f

=1Ф1

= 0.

При этом руководствуемся следующими правилами:

Вариант

I 2

Знак лелимого J-. + +

Знак лелтеля/i +

1,^,+11-2'"'"

А^>0

Л,

с, =

с,

= О

Послелова1ельность действий

для

получения цифр частно!

показана

1аблиис

6 I

Oimew

(Г ] =

0.11000.

Чго делать

С\М.

3FFaK ociaiKa

А^..

Цифра часттюго

••«,-1

+ й 2'" '

А,

>и

А,

с ,= I с, = О

А,_,

В2'<''"

Л,

А, < О

с = О с

•1,

в 2 I""

.4,

I, < О

с,

= О

с,

Т а б

и па

6.1

Суммаюр

1101100

11111001

0011001

1110010

1100101

00110111

1111110

1111101

0011001

0010111

ИЙОИО

11III01

null

0011001

0010101

поопо

1111011

III01II

ШЩ}

0010001

Регистр с

00000

оооо-

00001

0001-

0001

0011-

00110

lo-

ll 000

100-

11000

11римечание

И,

11.

СМ :=

{А\;^,.

РгЛ :=

{В\"^. l>iC

|CM):]ivr]:

1СМ]:=1СМ] + |ВЙ;

Л, <0-,С| =U

lCM);lKc|.

|CM):=|CM|

|«0,;

/1,

< 0: с,

lCM);irVr):

|CMl.= lCM)

lBft;

/f,

= 0;

Восстановление остатка

|СМ]:=1СМ]+|й1:5;

1СМ];|РГС|:

|СМ1:=1СМ1

|йа;

А,

> 0: с, = 0:

Восстановление осгагка

|СМ]:=1СМ] + 1ВЙ;

1СМ];1РГГ]:

|СМ]:=|СМ] + №;

А,

> 0:

<-•,

= 0;

Ко[!ен операции

6 2 Деление чисел, представленных в форме с фиксированной запятой

По своему характеру операция деления относится к операциям,

дающим не всегда точный результат, поэтому признаком окончания опе-

рации деления может быть достижение заданной точности (по сумме

сдвиговых сигналов). Если в процессе деления получили остаток Д =0,

то операция останавливается и в оставшиеся разряды частного записы-

вается нуль. Обычно формальным признаком конца операции деления

является количество сдвигов: при достижении числа сдвигов, равного

количеству разрядов в частном, вырабатывается сигнал окончания опе-

рации деления.

Требуется несколько интерпретировать правила определения цифры

час

ною. В примере 6.1 проводится сравнение знаков делимого и остатка

иа каждом шаге: при совпадении знаков в частном записывается единица,

при иесовпадеиии — нуль. Можно сравнивать знаки делителя и остатка,

тогда единица в 1)черелиой разряд частного записывается при иесовггадении

знаков, а нуль — при совпадении.

Для получения частного, представлен

HOI

о в обратном коде, все дейст-

вия должны осуществляться по следующим правилам:

Вариант

Знак ;!t'jmMm(i

3ii;iK jicjiHFCJiH

Чк) ;Eeii;irb » CM

Знак- ociaiKa .(,

Un(|)pa частою i

..(,

, +

Br^'-»

Л,

> и

с, =1

А,<0

с, =0

вое,

ост.

А,_,

В^2-"-»

Л, >0

?, =0

с, =1

А,<0

с, =1

с, =0

вое,

ост.

А,_,

+В 2 "^'>

/(,

г,

= 1

с, =0

вое.

ост.

/f, <0

/(,_,

+S'2-<'-"

/f, >0

с, =0

вое.

ост.

/1,

с, =1

г,

Пример fi.2. 1';илсл111ь числа .^==-0,10101 и Д = 0,11ШО на двоичном сумматоре обрат-

[I01

о кода с iinjiyHciHicM частного в обратном коде.

1'е

111

с и и с CipyKiypnaH схема и метол деления те же, что в примере 6.1.

!релс1?.!!им числа п обратных кодах:

|.4|^

= 11.01010; 1Д]^ =

11,00011;

[Щ"^ = 00.11100 .

Знак рс(ул1.!а[а Л^,. ^^ |фО = i .

I iocjiwioiiaiejibiiocib дейсший при решении задачи показана в таблице 6.2

Оптет {С^^^, ^П.ООШ.

Выполнение

операций

деления

чисел

на

двоичных

сумматорах

Г а б

л и

11 а 6.2

Сумматор

И010Ш

I010I0I

0011100

II10001

1100011

0011100

IIIMII

iiiim

0011100

IIOOOII

mini

iiiiiii

OUIIIOO

0011100

IIOOOII

IIIIIII

\nmi

0011100

Регистр С

««)00

0000-

00000

oooo-

00000

0000-

00001

0001-

0001 1

0011-

001II

И. ri,CM:=l/IU;Pfe.=

|см];

|Pi<1;

ICM]:=ICM]

IBC:

/fi < 0; c, = 0;

1СМ1;1РГС];

ICM]:=1CM]

+ IBU;

A,<0:cj=0: (.-lj=0);

lCM];liwi;

|CM1:=ICM] +

|«C;

/1,

>0;c, =0;

Восстановление остатка

[СКТЦКТ];

[CM1:=|CM] +

IBC;

>0.c,= 1;

Восстанонлеиие остатка

fcMl.lpSl;

|CM]:=ICM] + |B]^;

.4,

> 0; c, =

Хслв = 5 . Коней

Примечание

[Bu.i>rt-.= «.

Затраты времени на выполнение операции деления можно определить

по формуле

'де,

="['«. +(! +

/')'„].

(б'»)

где п — длина разрядной сетки;

1^^^

— время выполнения сдвига на один

разряд; /„ — время выполнения операции сложения; р ~ вероятность по-

явления нулей в разрядах частного.

На двоичных сумматорах дополнительного кода можно получить частное

как в прямом, так и в дополнительном кодах. Знак частного образуется отдель-

но от цифровой части путем сложения знаковых разрядов но модулю 2.

146

6 2 Деление чисел, представленных

форме

фиксированной запятой

Для получения частного в прямом коде правила остаются теми же, что

и для сумматоров обратного кода (см, пример 6.!).

Пример 6.3. Разделить число /^ = 0,1000!

иа

Д=-ПОП

на

двоичном сумматоре

до-

полнительного кода, qacTiFoe получить

тфямом коде. Используется структурная схема,

представленная на рис.

6.1,

о-

Решение, Поспедовательность действий при решении примера показана в таблице 6.3,

[А]^

00,10001;

[Д]"

11.00101;

1Д]"

=00,11011. Используем алгоритм без восстановле-

ния остатка. Знак

частно!

о;

Sgf- =

О Ф1

Таблица

CyMMaiop

0010001

0100010

1100101

00()() 111

0001110

1100101

II 1(1011

1100110

OOIHIJI

«OOOOOI

0000010

1100101

11001

100(110

0011011

II0I00I

Регистр

00000

0000-

00001

0001-

00010

0010-

00101

0101-

01010

1010-

10100

И.П.СМ:=И1;;РгС

[СМ];

|РгС];

lCM]:=lCM]

[iS|;;

/<1

> 0; с, =

(сМ];|РгС1;

ICM];=|CM]

|B|;;

А^

< 0; с, = 0;

[сЩ1РгП;

ICM];=[CM]

1B|;;

А,

> 0; с, =

|СМ];1РгГ);

[СМ]-.= 1СМ]

(в];;

А,

< 0;

С4

= 0;

(СМЦРгС);

|СМ];=1СМ]

1в];;

/f, < 0;

= 0;

£„,

= 5,

Конец

Примечание

= 0;PrB:=[Bj;:

Ответ:

[С]„^

=1.10100.

Ллгори! м выполнения операции деления должен работать так, что если

делитель равен О или делимое равно максимальному отрицательному чис-

лу, то вырабатывается сигнал переполнения.

147

6 Выполнение onepaifuu деления чисел на

Овоинны.х

сумматорах

Сигна/1 нереполнення должен вырабатываться и в тех случаях, когда

делимое больше делителя по абсолютной величине для чисел с фиксиро-

ванной занятой.

6.3.

Особенности деления чисел, представленных в форме

с нлавающей занятой

^Для получения частного отделения двух чисел, нредсьтвлениых в форме

с плавающей запятой, необходимо определить m^ - т

//;г^( . /;, - р

- р^ .

Так как мантиссы делимого и делителя

—-

нормализованные числа, при

делении возможны случаи, когда \т^\

^тц\;

[т ,| < \т„\.

Вели MaiiTHCca делимого больше или равна мантиссе делн!еля. ю в

конце операции деления потребуется нормализация частного (пар>и1енис

правой границы). Таким образом, а/поритм деления начинайся с операции

вычитания делителя из делимого и записи единицы в целую час!ь часиюго.

Все остальные действия над мантиссами аналогичны действиям над числа-

ми,

представленными в форме с фиксированной запятой.

Если мантисса делимого меньше мантиссы делителя, то |юсле операции

вычитания па первом uiaie получи^гся отрицательный остаток, что означает

нуль в целой части мантиссь! частного и продолжение алгоритма деления гго

рассмотренным выше правилам для чисел, представленных в форме с фикси-

рованной запятой. Таким образом, частное всегда получается в прямом коде,

а действия над мантиссами осуществляются на ДСОК njin ДСДК.

Так как при операции деления порядки чисел вычитаются (изображения

складываются), возможно переполнение разрядной сетки в сумматоре г!оряд-

ков.

При иере1юлнении в сторону отрицательных величин 1горядка мантисса

результата превращается в машинный нуль, а порядку присваивается наи-

большее отрицательное значение. Если делитель равен нулю, то таюке выра-

батываются сигналь!

ц> =

\ и останов машины. Эти nacTHbie случаи преду-

смотрены iipH реализации алгоритмов в ЕС ЭВМ, где используется а?1Горигм

деления без восстановления остатков. При этом мантисса делимого имеет

длину в два раза больше, чем делитель, что иллюстрируется примером 6.4.

Пример 6,4. Рэ)лелить число /1 = 0,100011 И

•

2' на Д =

0.1

111

PeuFeuMe- Рассматривается случай, котда |"'^|<1"1д|- Прежде неси» заммиьшакися

машинные изображения мантиссы делимого |wi^)" = 00.100011 11; мантиссы лслигсля

l^'wl" -00,1111 и

[Ш/,]'^

11,0001.

6.4 Ускорение операции деления

Все действия выполняются

на

сумматоре дополнительного кода

послеловательности,

>к<ваи!!0й

1аблице6

Таблица

CyMMaloji

00,10001111

01,00011110

"^11,0001

00,00101110

00,01011100

* 11,0001

11,01101100

10,1101 1000

* 00,1111

11,11001000

11,10010000

00,11 11

00,1000000(1

Pefис1р

0000

000-

0001

001

0010

010,-

0100

100

1001

Примечание

И. П. СМ := [mj

]";

РгС := 0; РгВ := |т„

слвиг суммагоров и регистров

|CM|:=|CM|

lm];;

с,

t;lBHF-

суммаюров и регистров

|СМ|=|СМ1

|Я„];;

Ci=0,

елниг суммаюров и регистров

|CMl:=|CM|+[m,i;;

= 0;

слвиг суммагоров и регистров

|СМ|:=|СМ|

|т,];,

с, =

Koircii

i:;

O.'innupcMciiin)

н1.Г!!|сляе]ся порядок частного с1гедугог1гим обратом: Рс-Р^-Рн-

0,011

0,010-0,001

гтоггре.чеяясгся зггак частою .Vg,. = О®

0=^

О-

Оттт

-0,1001

6.4.

Ускорение операции деления

Идея метода ускорения операции деления заключается в том, что в случае

обра^тванпя досгаючпо мшюго или достаточно большого по абсолютной ве-

jrHMiine остагка очередные цифры частного будут группой одинаковых цифр

либо nyjreH. jni6o единиц, гюэтому продолжение процесса деления обычным

способом иигитпе, так как эту группу цифр можно записать в частное сразу,

Рассмогрим примеры деления десятичных и двоичных чисел:

2281825

"2275

0()()6825

2275

1003

1010001

1001

0001001

lOOi

1001

6825

0000

1001

0000

6 Выполнение операций деления чисел на двоичных

сулглгатора^^

Здесь на первом шаге получился малый по величине положительный

остаток, который содержит нули в трех старших разрядах. В частном после

первой цифры записаны нули в два следующих разряда. Можно утвер-

жда1ь, что при малом положительном остатке в частное можно сразу запи-

сагь к -

нулей в соответствующие разряды, остаток сдвинуть на к разря-

дов влево, BbiMecTb из него делитель и далее продолжить операцию деления.

Если в результате вычитания на каком-то шаге получается большой

положительный остаток, в котором к старших разрядов содержат единицы

(для двоичных чисел), то гю меньшей мере в (к~\)-е разряды частного

можно записать единицу;

1000000000... 110001

10001 ГТТТТО

omjo

10001

опою

10001

_0100(0

10001

000001...

Таким образом, в данном случае процесс деления должен осугцесгв-

лягься комбинирова1Н1ым сгюсобом, с анализом (юследовательносги нулей

(если остаток положительный) или последовательности единиц (если оста-

ток отрицательный) в старших разрядах остатка. При обнаружении такой

последовательности длиной к сразу можно записать в (А: -1 )-е разряды ча-

стного соответственно нули или единицы. После этого провести сдвиг" на

(^ -

) разряд и продолжить операцию деления.

В других случаях операция выполняется по обычному алгоритму.

Рассмотренный метод ускорения операции деления может дать эффею

только тогда, когда встречаются последовательности нулей или единиц в

остатках.

Для ускорения операции деления можно воспользоваться также мето-

дом одновременного определения двух цифр частного, который являе!ся

развитием изложенной выше идеи. Этот метод реализован в некоюрых

ЭВМ третьего поколения.

I\ycib А - делимое; В — делте;гь; Д_| — остаток па (/-I )-м шаге де-

ления.

Для остатка справедливо

> |Д_|| < В .

150