Щипицын А.Г., Кощеев А.А., Алешин Е.А., Павловская О.О. Элементы прикладной теории надежности
Подождите немного. Документ загружается.

плотности вероятности
() ( )
∫
ξξ=
t
dFtf
0
и конечные моменты 1-го и 2-го порядков (что достаточно очевидно):
[
]
i
MT
τ
=
0
,
.
[]
i
D τ=σ
2
Допущения о законах выполняются достаточно точно при замене отказавших
элементов на новые однотипные элементы и приближенно – при замене на отре-
монтированные элементы.
Моменты отказов (или восстановлений) t
i
образуют некоторый случайный по-
ток (последовательность случайных величин, рис. 3.1)
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
τ++τ+τ=
τ+τ+τ=
τ+τ=
τ
=
., . .
; ...
. . .
;
;
;
21
3213
212
11
nn
t
t
t
t
(3.1)
который является математической моделью процесса восстановления. Точки t
i
называются событиями этого потока. Изучение процесса восстановления сводится
к вычислению некоторых характеристик этого потока. Чаще всего интересуются
числом отказов ν(t) на интервале. Очевидно, что ν(t) является дискретной случай-
ной величиной, принимающей только целые и неотрицательные значения.
Найдем распределение случайной величины ν(t), т. е. вероятность того, что на
интервале
[
будет не менее n отказов:
]
t ,0
(){}
{
}
{
}
()
()
tFtPttPntP
nnn
=<
τ
+
+
τ
+
τ
=
<
=
≥ν ...
21
. (3.2)
Таким образом, задача сводится к нахождению закона распределения суммы
случайных величин τ
i
, которая в общем случае решается достаточно сложно. В
предположении о независимости слагаемых решение значительно упрощается.
Плотность вероятности суммы двух независимых случайных величин
можно найти как свертку плотностей вероятностей слагаемых:
21
τ+τ=t
()
() () () ( ) ( ) ( ) ()
τττ−=ττ−τ=∗=
∫∫
dftfdtfftftftf
tt
2
0
12
0
11212
(3.3)
или, учитывая, что , получаем .
() ()
ττ=
∫
dftF
t
0
()
() ( ) ()
ττ−=
∫
2
0
12
dFtftf
t
Обычно удобнее вычислять функцию распределения:
()
()
()
() ( ) () ( ) () () ( )
τ−τ=ττ−=τττ−=ττ=
∫∫∫∫∫
tdFFdFtFddFtfdftF
ttttt
2
0
12
0
1
0
2
0
1
0
22
. (3.4)
31

Для суммы трех случайных величин
(
)
321
τ
+
τ
+
τ
=
t
, очевидно, что
()
()
()
()(
ττ−=
∫
3
0
23
dFtFtF
t
)
)
)
. (3.5)
Вообще, для суммы n независимых случайных величин их функция распре-
деления находится как рекуррентная свертка:
()
()
()
()(
ττ−=
∫
− n
t
nn
dFtFtF
0
1
. (3.6)
Учитывая, что законы распределения случайных величин τ
i
одинаковы
( ), имеем
() ()
tFtF
i
=
(){}
()
()
()
()(
ττ−==≥ν
∫
−
dFtFtFntP
t
nn
0
1
. (3.7)
Таким образом, определение вероятности события
(
)
nt ≥
ν
сводится к вычис-
лению n-кратной свертки (3.7) законов распределения времени жизни.
Рассмотрим некоторые частные случаи.
1) . 0=n
Так как событие достоверно по построению, то
()
0≥ν t
(
){}
()
(
)
(
)
(
)
ttFtFtP 10
00
=
=
=
≥ν
.
2) . 1=n
()
() () (){ } ()()()()(){
τ<==ττ−=ττ−=≥ν==
∫∫
tPtFdFtdFtFtPtFtF
tt
00
011
11
}
. (3.8)
Вычисление в общем виде для 1 функции >n
(
)
tF
n
в большинстве случаев не-
возможно. Более того, даже для конкретного закона распределения
(
)
tF не всегда
получается аналитическое выражение для n-кратной свертки. Задача достаточно
легко решается только для экспоненциального закона надежности:
()
t
etF
λ
−
−=1,
(
)
dttdF
t
e
λ
−
λ= ,
()
()
()
[]
tt
t
t
eeee tdtF
λ−λ−λτ−τ−λ−
λ−−=τλ−=
∫
1 1
0
2
. (3.9)
Можно показать, что n-кратная свертка для экспоненциального закона имеет
вид
()
()
(
)
()
t
n
k
k
n
e
k
t
tF
λ−
=
−
∑
−
λ
−=
1
1
! 1
1
. (3.10)
Найдем вероятность того, что за время t произойдет ровно n отказов. Для этого
рассмотрим следующие события:
32

(){}
nt ≥ν=A,
(
)
{
}
1B
+
≥
ν
=
nt ,
(
)
{
}
nt =
ν
=
C.
В силу построения событий A, B и С видно, что ,
AB ⊂
B
\
AC = . Тогда
{}
{
}
{
}
{
}
BAB\AC PPPP
−
=
=
или в наших обозначениях
(){}()
(
)
{
}
(
)
{
}
()
()
()
(
)
tFtFntPntPtPntP
nnn 1
1
+
−
=
+
≥
ν
−
≥
ν
==
=
ν . (3.11)
В частности, при экспоненциальном законе надежности, учитывая соотноше-
ние (3.10), имеем
()
(
)
t
n
n
e
n
t
tP
λ−
λ
=
!
, (3.12)
откуда видно, что число отказов сильно уменьшается с ростом времени.
Выражения (3.2 – 3.7, 3.11) и дают искомую статистику процесса с мгновен-
ным восстановлением. Однако вычисление n-кратных сверток законов распреде-
ления (3.7) представляет собой трудоемкую задачу, поэтому рассматривают более
простые числовые характеристики процесса восстановления (или дискретной слу-
чайной величины ν(t)). Важнейшей из них является функция восстановления H(t),
равная среднему числу отказов на интервале времени
[
]
t ,0:
() ()
[]
()
()
()
()
()
[
∑∑
∞
=
+
∞
=
−==ν=
1
1
1 n
nn
n
n
tFtFntnPtMtH
]
. (3.13)
Непосредственное использование (3.13) неудобно, так как опять же требует
вычисление (n+1)-кратной свертки. Поэтому вместо функции восстановления час-
то применяют дифференциальную характеристику – плотность восстановления
h(t). Согласно определению имеем
() ()
(
)
(
)
t
tHttH
tH
dt
d
th
t
Δ
−
Δ
+
==
→Δ 0
lim , (3.14)
и плотность восстановления может быть интерпретирована как среднее число от-
казов, происшедших в единицу времени. Поэтому величина h(t) имеет еще и спе-
циальное название – средняя частота отказов и специальное обозначение ω(t).
По определению процесса восстановления оценкой средней частоты отказов
ω(t) является величина
() ()
(
)
tN
tn
tht
**
Δ⋅
Δ
==ω , (3.15)
где – число отказавших элементов за время Δt; N – число испытываемых
элементов, причем N = const, так как отказавшие образцы заменяются. При
(
tn Δ
)
∞→
N
эта оценка по вероятности сходится к средней частоте отказов.
Найдем связь функций H(t) и h(t) с характеристиками надежности самого эле-
мента, используя формулы (2.10, 3.15) для оценок
(
)
t
*
ω и . На интервале
возможны отказы двух видов (рис. 3.2).
()
tq
*
[
ttt Δ+ ,
]
33

1) Могут в первый раз отказать элементы, поставленные в работу в момент
времени 0
=
t
, т. е. работающие до первого отказа, с частотой отказов
(
)
tq
. Число
таких элементов
(
)
(
)
(
)
tNtqtNtqtn
*
Δ=Δ=
1
. (3.16)
2) Могут отказывать только элементы из числа восстановленных (заменен-
ных) на интервале 0 – t. Пусть
[
]
τ
Δ
+
τ
τ
, – некоторый промежуток времени, пред-
шествующий интервалу
[
ttt
]
Δ
+ ,, т. е. τ < t (см. рис. 3.2). За время Δτ из строя
выйдут
()
(
)()
tNttNtn
*
Δω=Δ=τ ω
2
элементов, которые восстанавливаются, и за
время
[
(элементы теперь работают до первого отказа) из них откажут
]
ttt Δ+ ,
()
(
)
(
)
(
)()
tttqNttqntn Δτ−
Δ
τ
ω
=
Δ
τ
−
τ
Δ
=
Δ
22
. (3.17)
t
0
τ
t
Рис. 3.2. Два типа отказов на интервале [t, t+
t+Δt
+
τ
Δ
τ
Δ
t]
Для нахождения общего числа отказов 2-го вида интегрируем (3.17) по всем
промежуткам Δτ от 0 до t:
() () () ()()
∫∫
Δτ−τωΔ=Δτ−Δτω=
tt
ttqtNtttqNtn
00
2
. (3.18)
Тогда общее число отказов всех типов на интервале
[
]
ttt Δ+ , равно
( ) () () () ()( )
∫
−Δ+Δ=+=Δ
t
dtqtNtNtqtntntn
0
21
τττω
. (3.19)
Разделив обе части (3.19) на NΔτ и учитывая (3.15), получим
() () ()( ) () ( )()
∫∫
−+=−+=ω
tt
dqttqdtqtqt
00
τττωτττω
(3.20)
или (так как )
() ()
tHt
′
=ω
() () ( ) () () ( ) ()
() () ( ) () ( )()
() ( ) ()
.τ
ττττωττ
τττωτττω
0
000
0000
τ−+=
=−+=−+=
=−+=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−+=
∫
∫∫∫
∫∫∫∫
FdtHtF
dqtHtFdttdqtF
dtdqttPdtdqttqtH
t
ttt
tttt
(3.21)
34
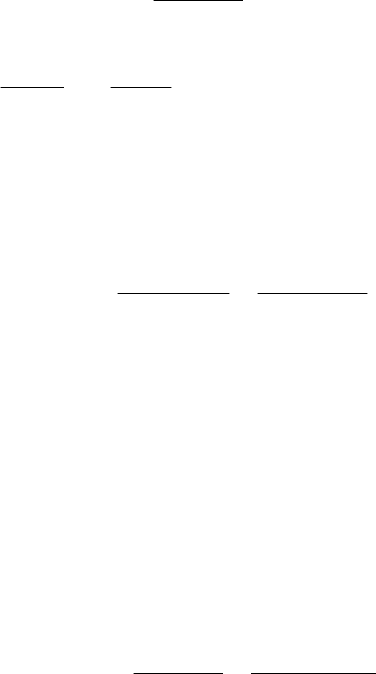
Уравнения (3.20, 3.21), представляющие собой интегральные уравнения Воль-
терра второго рода с разностным ядром, позволяют по известным плотностям ве-
роятности отказов или законам распределения
()
tq
(
)(
tQtF
)
=
найти среднее чис-
ло отказов (функцию восстановления)
(
)
tH
(
)
или среднюю частоту отказов t
ω
.
тных свер-
Решение уравнений (3.20, 3.21) обычно проще, чем вычисление n-кра
ток (3.13). Например, можно воспользоваться преобразованием Лапласа:
£ £
⎪
⎬
⎫
⎪
⎨
⎧
−+
∫
t
dtqtq τττω
£
()
=ω p
(){}
=ω t
() () ( )
=
⎪
⎭
⎪
⎩
0
=
£
(){}
tq
()( )
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
−
∫
t
dtq
0
τττω
+
⎧
(
)
(
)
(
)
pqppq
⋅
ω
+
=
,
откуда
(
)
()
()
pq
p
−
=ω
1
. (3.22)
Учитывая, что
pq
()
()
(
)
dt
tdP
dt
tdF
tq −==
, а
(
)
00
=
F и
(
)
10
=
P – начальные условия,
пол
учаем
(
)
(
)
(
)
ppPppFpq
−
=
=
1
.
а
Тогд
()
(
)
()
(
)
()
ppPppF
ppF
p
ppP
−
=
−
=ω
1
оотношения можно лучить фун
:
£
1
. (3.23)
Аналогичные с по и для кции восстановления
()
tH
()
=pH
(
){}
=tH £
=
£
() ( ) ()
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
τ−+
∫
FdtHtF
t
0
τ
(
){}
+tF £
()()
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
τ−
∫
FdtH
t
0
τ
(
)
(
)
(
)
pqpHpF
⋅
+
,
(
)
()
(
)
()
()()
pqppq
pH
−
=
−
=
11
. (3.24)
Такой прием позволяет просто вычислить изображение функции
pqpF
(
)
tH или
сложности возникают только при выполнении обратного преобразования
Лапласа.
Большинство практически важных задач решаются, используя введенные ха-
рактерист осстановления.
()
tω ,
ики процесса в
35

3.1.2. Задача о запасных элементах
Необходимо найти минимальное число запасных элементов n, которых с веро-
ятностью не меньшей
α
−=1
0
P
хватит на заданное время работы T. Выбор значе-
ния P
0
(доверительная вероятность) обычно производится из стандартного ряда
0,9; 0,95; 0,99 (или уровень значимости α берется из ряда 0,1; 0,05; 0,01).
Чтобы n элементов хватило (для замены отказавших) на время T, за этот про-
межуток времени должно быть не более n отказов, т. е.
()
nT ≤
ν
. Согласно усло-
вию задачи
(){}
α
−
==≤ν 1
0
PnTP
или
(
)
{
}
α
=
>
ν
nTP ,
тогда
(
)
{
}
α
≤
+
≥
ν
1nTP . (3.25)
Учитывая (3.7), получаем
()
(
)
α
1
≤
+
TF
n
. (3.26)
Наименьшее число n, при котором выполняется (3.26), и дает решение задачи.
Следовательно, при решении задачи о запасных элементах необходимо вычис-
лять n-кратные свертки функции
(
)
tF , что в общем случае возможно только чис-
ленно. В конечном виде свертка находится лишь для трех распределений – экспо-
ненциального, нормального и Г-распределения.
Пусть надежность элемента подчиняется экспоненциальному закону, для ко-
торого
()
t
etF
λ
−
−=1, а
()
t
etP
λ
−
= . Пусть
час
1
3
10
−
=λ
,
0,05=
α
. Тогда, с учетом
соотношений (3.10) и (3.26), получаем
()
()
(
)
()
0,05
! 1
9
19000
9
1
1
1
1
≤
−
−=
−
+
=
−
+
∑
e
n
k
k
n
k
F
.
Если n = 12, то
()
()
0,050,0749000
13
>
=
F . При n = 13,
()
()
0,050,0419000
14
<
=F .
Значит, n = 13 является решением задачи о запасных элементах.
Увеличивая доверительную вероятность P
0
(уменьшая уровень значимости α),
следует ожидать рост числа запасных элементов. Действительно, для тех же ис-
ходных данных, но при запасных элементов потребуется уже 17 (n = 16,
; n = 17,
0,01=α
()
()
0,010,0119000
17
>=F
()
(
)
0,010,0029000
18
<
=
F ).
3.1.3. Поток Пуассона
Для экспоненциального закона надежности вероятность того, что за время t
произойдет ровно n отказов, согласно выражениям (3.10 – 3.12), равна
(){}()
()
()
()
()
(
)
t
n
nnn
e
n
t
tFtFtPntP
λ−
+
λ
=−===ν
!
1
. (3.27)
Таким образом, распределение числа отказов ν(t) на интервале подчиняется
закону Пуассона.
[
t ,0
]
36

Согласно соотношениям (3.13) и (3.27), функция восстановления (для экспо-
ненциального закона) имеет вид
() ()
(
) ()
()
t
n
t
t
n
t
ntnPtH
n
n
t
n
t
n
n
n
ee λ=
−
λ
λ=
λ
==
∑∑∑
∞
=
−
λ−
∞
=
λ−
∞
= 1
1
11
! 1
!
(3.28)
(так как
()
()
t
n
n
e
n
t
λ
∞
=
−
∑
=
−
λ
1
1
! 1
), а средняя частота отказов определяется как
(
)
(
)
λ
=
′
=
ω
tHt . (3.29)
Эти же соотношения можно найти из решения интегральных уравнений Воль-
терра (3.20, 3.21). Действительно, так как
(
)
t
etF
λ−
−=1,
()
t
etq
λ
−
λ=
, то
()
()
λ+
λ
=
pp
pF
,
()
λ+
λ
=
p
pq
. Учитывая выражения (3.22 – 3.24), имеем
()
2
p
pH
λ
=
,
()
p
p
λ
=ω
.
Тогда
()
=
tH £
-1
(
)
{
}
=
pH
£
-1
t
p
λ=
⎭
⎬
⎫
⎩
⎨
⎧
λ
2
,
(
)
=
ω
t £
-1
λ=
⎭
⎬
⎫
⎩
⎨
⎧
λ
p
.
Из формул (3.28), (3.29) видно, что при экспоненциальном законе надежности
параметр потока отказов λ не зависит от времени, а среднее число отказов
(
)
tH
прямо пропорционально длине интервала времени. Процесс восстановления с та-
кими характеристиками образует, так называемый, простейший поток событий
(отказов) или однородный процесс Пуассона (пуассоновский поток). Естественно,
поток Пуассона является идеализацией реальных потоков отказов, (так как экспо-
ненциальный закон описывает нестареющие элементы), но, несмотря на это, ши-
роко применяется на практике.
Рассмотрим основные свойства пуссоновского процесса.
1) Стационарность
Вероятность того, что на некотором интервале времени произойдет опреде-
ленное количество событий (отказов), не зависит от расположения этого интерва-
ла на временной оси, а определяется только длиной интервала и числом событий
(т. е. процесс Пуассона является марковским случайным процессом).
2) Отсутствие последействия
Это означает, что вероятность наступления некоторого числа событий потока
на промежутке Δt не зависит от того, сколько отказов было до этого (условная ве-
роятность появления k отказов в интервале Δt совпадает с безусловной вероятно-
стью).
37
3) Ординарность
Вероятность наступления более чем одного события потока (отказ) за малый
промежуток времени есть величина бесконечно малая по сравнению с длиной ин-
тервала Δt:
(
)
{
}
(
)
tOtP
Δ
=
>
Δ
ν
1 . (3.30)
t
Δ
Это означает, что на малом интервале
практически невозможно наступле-
ние более чем одного отказа.
Во многих случаях поток Пуассона хорошо аппроксимирует реальные потоки
отказов (например, в сложных электронных схемах). Проверка на практике усло-
вий стационарности, отсутствия последействия и ординарности для установления
пуассоновости случайного процесса, как правило, является сложной процедурой.
Чаще пользуются теоремой Григелиолиса, смысл которой заключается в том, что
если система состоит из большого числа высоконадежных элементов, отказы ко-
торых можно считать независимыми, то суммарный поток отказов в системе бли-
зок к пуассоновскому.
Укажем еще два интересных свойства пуассоновского потока:
а) если известно, что в определенном интервале времени наступили n собы-
тий потока, то моменты наступления этих событий независимы между собой и
равномерно распределены в этом интервале;
б) суммарный поток, образованный наложением двух независимых потоков
Пуассона с интенсивностями λ
1
и λ
2
, также является пуассоновским с интенсивно-
стью λ = λ
1
+ λ .
2
Если время жизни элемента распределено не экспоненциально, то поток отка-
зов отличается от пуассоновского. Известно несколько различных моделей пото-
ков [8], каждая из которых применяется в своем конкретном случае.
3.1.4. Оценки функции восстановления
Сложности в вычислении n-кратных сверток приводят к тому, что часто при-
ходится строить оценки характеристик процесса восстановления. Например, оце-
ним функцию восстановления
(
)
tH .
По определению функции восстановления (3.13) имеем
()
()
()
()
()
[]
()
()
()
()
()
() ( )
()
()
()
()
.1
121
1
1
11
1
∑∑∑
∑∑∑
∞
=
∞
=
∞
=
∞
=
+
∞
=
∞
=
+
=−−=
=−=−=
n
n
n
n
n
n
n
n
n
n
n
nn
tFtFntnF
tnFtnFtFtFntH
. (3.31)
В частности,
() ()
()
()
∑
∞
=
=
′
=ω
1n
n
tftHt
. (3.32)
Так как члены ряда (3.31) – функции распределения, то они неотрицательны.
Тогда получаем нижнюю оценку функции восстановления:
38

(
)
()
(
)
(
)
tFtFtH
=
≥
1
. (3.33)
Для построения верхней оценки рассмотрим два события:
{
}
tt
n
<
= A
и ,
}{ maxB
1
t
k
nk
<τ=
≤≤
.
где
nn
t τ
+
+τ+τ= ...
21
Из очевидного неравенства
nnk
nk
t
τ
+
+
τ
+
τ
=
<
τ
≤≤
... max
21
1
следует, что
()
() ( )
max
1
⎟
⎠
⎞
⎜
⎝
⎛
<τ≤<=
≤≤
tPttPtF
k
nk
nn
. (3.34)
}
{
max
1
t
k
nk
<τ
≤≤
{
}
ttt
n
<
τ
<
τ
<
τ
..., , ,
21
События
и эквивалентны по построению.
Поскольку, по предположению, времена жизни τ
i
являются независимыми, одина-
ково распределенными случайными величинами, то
{ } { } () ()
tFtFtPtttPtP
n
n
i
i
n
i
ink
nk
==<τ=<τ<τ<τ=<τ
∏∏
==
≤≤
11
21
1
..., , , max }{
и, учитывая (3.34),
()
(
)
(
)
tFtF
n
n
≤ . (3.35)
Заменяя слагаемые в (3.31) их оценками (3.35), получаем верхнюю оценку
функции восстановления:
() ()
∑
∞
=
≤
1n
n
tFtH
. (3.36)
(
)
1
<
tF
Для любого конечного момента t функция
, тогда правая часть (3.36) –
бесконечно убывающая геометрическая прогрессия со знаменателем, равным
. Следовательно, верхняя оценка принимает вид
()
tF
()
(
)
()
tF
tF
tH
−
≤
1
. (3.37)
Таким образом, объединяя (3.33) и (3.37), получаем
() ()
(
)
()
tF
tF
tHtF
−
≤≤
1
. (3.38)
Из формулы (3.38) видно, что для начального участка эксплуатации, на кото-
ром функция распределения
(
)
1
<
<tF ,
(
)
(
)
tFtH
≈
.
Для экспоненциального закона надежности, согласно (3.38), получаем
(
)
11 −≤≤−
λ
λ
−
tt
ee tH . (3.39)
39
Точность оценок функции восстановления уменьшается с ростом t. На малом
интервале можно считать, что
] ,0[
оц
t
(
)
(
)
tFtH
≈
. Для практических приложений
приемлемо
λ≈ 3,0
оц
t
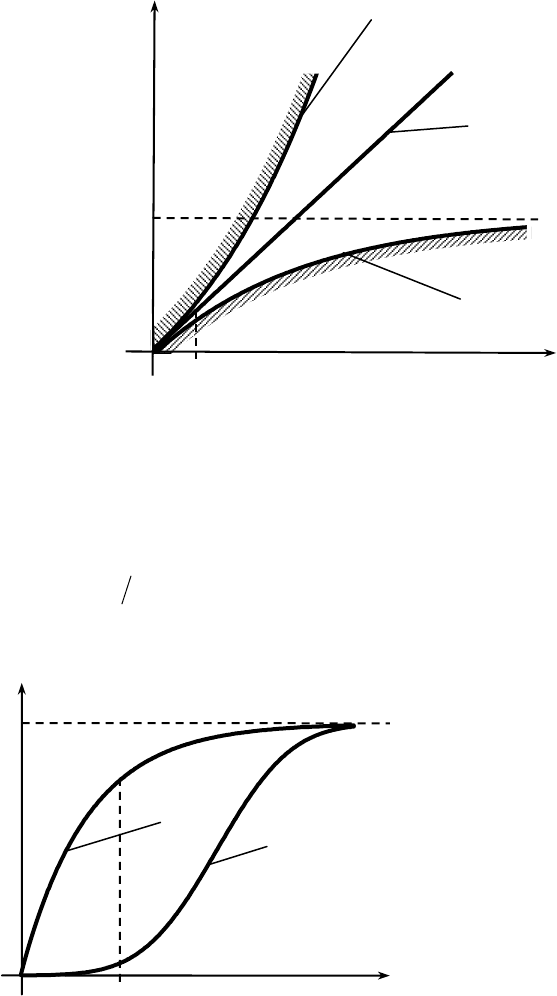
(рис. 3.3). По виду функции
(
)
tF можно судить о функции
восстановления (рис. 3.4).
3.1.5. Основные теоремы теории восстановления
Рассмотрим некоторые важные свойства процесса восстановления для доста-
точно большого интервала t, что представляет практический интерес, когда необ-
ходимо узнать поведение объекта после большого числа восстановлений. Мате-
матически это означает изучение асимптотических свойств характеристик про-
цесса восстановления при
∞
→
t
[12].
0
t
1
Рис. 3.4. Оценка среднего числа
отказов на малом промежутке
времени
] ,0[
оц
t :
для элементов вида 1 среднее
число отказов меньше, чем для
элементов вида 2
F(t)
1
2
оц
t
1
0
H(t) = λt
H(t)
t
Верхняя оценка,
1−
λ
t
e
Нижняя оценка,
t
e
−
λ
−1
t
оц
≈ 0,3/λ
Рис. 3.3. Оценки функции восстановления для
экспоненциального закона надежности
40
