Shani G. Radiation Dosimetry: Instrumentation and Methods

Подождите немного. Документ загружается.

350

Radiation Dosimetry: Instrumentation and Methods

rate

dose-response characteristics of a ferrous-sulphate-

doped chemical dosimeter system (Fe MRI) immobilized

in a gelatin matrix were explored by Hazle et al. [2] Samples

containing various concentrations of the FeSO

dosimeter

were irradiated to absorbed doses of 0–150 Gy.

relax-

ation rates were determined by imaging the samples at a

ﬁeld strength of 1.5 T(

H Lamor frequency of 63.8 MHz).

The response of the system was found to be approximately

linear up to doses of 50 Gy for all FeSO

concentrations

studied (0.1–2.0 mM). Changing concentrations in the

range of 0.1–0.5 mM affected both the slope and intercept

of the dose response curve. For concentrations of 0.5–2.0

mM, the slope of the dose-response curves remained con-

stant at approximately 0.0423 s



in the dose range of

0–50 Gy.

The gels were prepared by mixing 5% gelatin by

weight with 75% of the total desired volume of water

under constant heating and stirring. This particular gelatin

was used because of its high bloom rating (higher bloom

ratings indicate stronger or more viscous gels), allowing

for lower concentrations of the gel to achieve an accept-

able thickness. De-ionized water was used to avoid con-

tamination with other paramagnetic species. The inorganic

components were mixed in 25% of the desired total

volume at or below room temperature. The resulting ﬁnal

concentrations (for the total volume) were 0.1–2.0 mM

FeSO

, 1 mM sodium chloride and 0.5 M sulphuric acid.

After the gelatin had been allowed to melt completely at

55°C for at least 15 min, heating was discontinued and

the solution containing the inorganic components was

added. The gel was then allowed to cool with continual

mixing for 30–60 min. After the nominal cooling period,

the gel was transferred into 12-mm-diameter polypropy-

lene tubes and allowed to harden at room temperature for

at least 1 h. At this point the gels had congealed to a semi-

solid state and did not require refrigeration. After the

samples were positioned in the tank, the tank was ﬁlled

with tap water at room temperature and the gels were

allowed to equilibrate for approximately 15 min to the

ambient temperature of the tap water (typically 22–24°C).

The water tank served to maintain constant temperature

and to reduce magnetic susceptibility artifacts at the

external interface of the gel samples. Tap water was used

in the tank (

typically 0.333 s



) rather than paramag-

netically dopted water (

typically 1.25 s



), as is the

usual case in MRI studies, so that the ambient water

surrounding the samples would have low signal intensity

for all but the images obtained using extremely long

repetition times. [2]

The NMR experiments were carried out using a 1.5-T

Signa whole-body scanner. The longitudinal relaxation

rates were determined using seven single-slice images of

the same spatial location acquired with different repeti-

tion times by saturation recovery analysis. Typical rep-

etition times were 100, 300, 600, 1000, 1500, 3000, and

6000 ms. Single-slice images were obtained in lieu of

multi-slice images to avoid any out-of-plane saturation

effects.

was calculated using a three-parameter ﬁt of

the equation below, using the standard region-of-interest

software provided with the system:

(7.6)

where

(

) is the magnetization observed at a repetition

time

is the equilibrium magnetization (



0) and



is the read-pulse ﬂip angle (nominally 90°).

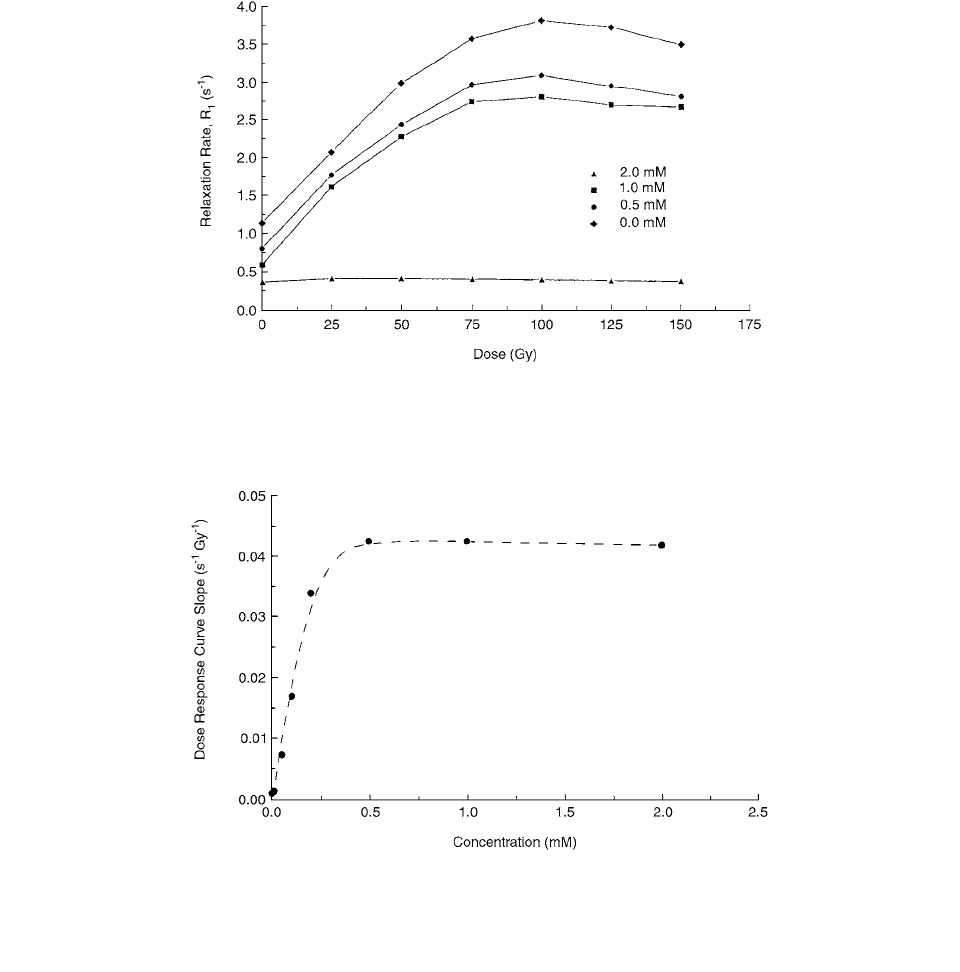
The general dose response of the dosimeter was deter-

mined by irradiating gels of 0.0, 0.5, 1.0, and 2.0-mM

FIGURE 7.1

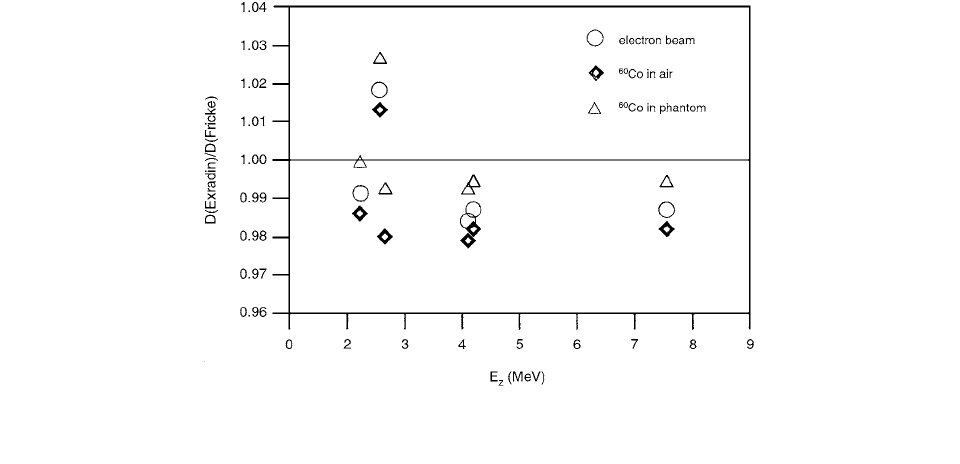
The ratio of the values of the absorbed dose to water determined with the Extradin chamber, calibrated using three

different calibration methods and Fricke dosimetry. (From Reference [1]. With permission.)

() M

1 1 cos



()e



[]

CH-07.fm Page 350 Friday, November 10, 2000 12:03 PM

Chemical Dosimetry

351

FeSO

to doses of 0–150 Gy. A single sample was irra-

diated for each dose level. The results of this experiment

(Figure 7.2) suggest that the linear range of the system

for the concentrations considered is 0–50 Gy, irrespec-

tive of FeSO

concentration. The useable range could be

extended to 100 Gy if higher-order response terms are

acceptable.

To demonstrate the effect of concentration on sensi-

tivity, the slopes of the response curves were plotted

against concentration (Figure 7.3). Increasing FeSO

con-

centration affects not only the initial

but also the slope

of the dose-response curves for concentrations up to about

0.5 mM. [2]

The mean absorbed dose in the detection volume of

Fricke dosimeters can be written

(7.7)

where

(Fe



) is the radiation chemical yield of the oxida-

tion of ferrous ions into ferric ions,



is the molar extinction

coefﬁcient of ferric ions at the considered wavelength,



is the density of Fricke solution,

is the light pathlength

through the spectrophotometer cell, and



(

) is the

increase in optical density of the solution. Direct dose mea-

surements require knowledge of all the above parameters.

FIGURE 7.2

The dose-response curve for a gel concentration of 5% and FeSO

concentrations of 0.0, 0.5, 1.0, and 2.0 mM are

shown for dose up to 150 Gy. The usable range seems to be 0–50 Gy. (From Reference [2]. With permission.)

FIGURE 7.3

The slopes of the dose-response curves plotted as a function of initial FeSO

concentration to demonstrate the effect

of concentration on dose-response sensitivity. In the range of 0 mM to about 0.5 mM, increasing the FeSO

concentration results in

increasing sensitivity. Concentrations in the range of 0.5 to 2.0 mM have approximately constant sensitivity (average



0.0423



). (From Reference [2]. With permission.)

〈〉  OD()/





G Fe

()

CH-07.fm Page 351 Friday, November 10, 2000 12:03 PM

352 Radiation Dosimetry: Instrumentation and Methods

The transfer method uses the ratio of absorbed doses in the

detection volume of the transfer dosimeter in both phan-

toms. After simpliﬁcation, this ratio reduces to the ratio of

instrument responses, either ionization currents or increases

in optical density. In particular, the constants W

air

G(Fe

3

) and their associated uncertainties are eliminated.

Chauvenet et al. [3] discussed the ratio of dose

absorbed in the detecting material vs. the dose to the

wall.The dosimeter is made of a detection volume V, ﬁlled

with material “det” surrounded by a wall of material

“wall.” The fraction of dosimeter response due to electrons

arising in the detection volume is noted



det

, and the frac-

tion of dosimeter response due to electron arising in the

dosimeter wall, is



wall

. The correction factor for the per-

turbation of photon energy ﬂuence at point C, caused by

the replacement of medium “med” by material “wall” in

the volume of the wall, is denoted

wall

(



)

med,wall

; the same

correction factor caused by the replacement of medium

“med” by material “det” in the detection volume is

denoted

med

(



)

med,det

. Similar symbols are used for stop-

ping power and absorption coefﬁcient ratios. The corre-

sponding absorbed-dose to collision-kerma ratios are

denoted



med,wall

and



med,det

. Using these notations, the

absorbed dose in medium “med” at point C without dosim-

eter, D

med

(C), and the mean absorbed dose in the detection

volume V of the dosimeter, are then related by [3]

(7.8)

Equation (7.8) is applied to two identical Fricke

dosimeters with glass walls. The optical density increase

caused by the production of Fe

3

ions under irradiation

was measured by spectrophotometry at a wavelength of

304 nm, relative to a blank realized with a non-irradiated

sample. The measured optical densities are corrected for

irradiation temperature (t

) and reading temperature (t



according to the following formula:

(7.9)

Correction factors for photon ﬂuence perturbation

wall

(



)

med,wall

and

det

(



)

med,det

are evaluated by derivation of

the ratio of transmissions through the zone corresponding

to the wall or to the detection volume ﬁlled with appropriate

materials. For this purpose, the following parameters are

introduced: (1) the effective attenuation coefﬁcient , (2)

the effective mean wall thickness x, and (3) the effective

mean distance d between the front face of the wall-detection

volume interface and the median plane of the detection

volume perpendicular to the beam axis. From these consid-

erations, the following relations can be derived:

(7.10)

(7.11)

Coefﬁcients



det

and



wall

can be expressed as follows,

with reasonably good approximation:

(7.12)

(7.13)

where u

wall

is the ratio of absorbed doses to the wall at the

outer interface and at the inner interface; t

wall

is the photon

energy ﬂuence transmission through the wall; is

the mean value of the ratios of absorbed doses to material

“det” at each point of V and at the wall interface, averaged

over the whole detection volume V; and is the mean

value of the photon energy ﬂuence transmission through

“del” from the wall interface to each point of volume V,

averaged over the volume V. According to the exponential

decay and build-up assumption of electron ﬂuence (Burlin

[10]) or, more exactly, of energy deposition, one can write

(7.14)

(7.15)

where



e,wall

and



e,det

are effective attenuation coefﬁcients

for electron energy deposition in materials “wall” and

“det,” respectively; is the mean wall thickness for

electrons arising in medium “med”, and is the mean

effective thickness of volume V(  2d).

The EGS4 Monte Carlo calculation for a 1-mm-thick

Pyrex wall yielded



det

 0.89 and



wall

 0.10. [3] Therefore,

(7.16)

Chauvenet et al. obtained

(7.17)

Dose conversion and wall correction factors for Fricke

dosimetry in high-energy photon beams were calculated

by Ma and Nahum [4], using both an analytical general

cavity model and Monte Carlo techniques. The conversion



det

〈〉

med

C() D

det

〈〉

wall



()

med,wall,det



()

med,det





wall





det

()S

med,det







wall





()

med,wall

wall,det





()

med,det

]

 OD()



 OD()

uncorrected

1 0.0069 t



20()()1 0.0012 t

20()()

---------------------------------------------------------------------------------------------------------------







()

wall med,wall

exp (





med

x )/exp (





wall

x )



()

det med,det

exp (





med

x) /exp (





det

x)



det

1 u

det

〈〉/ t

det

〈〉()



wall

1 u

wall

()()u

det

〈〉/ t

det

〈〉()

wall

()[]1



det

()

det

〈〉

det

〈〉

wall

exp



e wall,

x()

det

〈〉 1 exp



e,det

y()[]



e,det

y

x

y

C() D

〈〉 fP

wall

1.0037 10()

C() D

〈〉 1.0026 24()

CH-07.fm Page 352 Friday, November 10, 2000 12:03 PM

Chemical Dosimetry 353

factor is calculated as the ratio of the absorbed dose in

water to that in the Fricke dosimeter solution with a water-

walled vessel. The wall correction factor accounts for the

change in the absorbed dose to the dosimeter solution

caused by the inhomogeneous dosimeter wall material.

It is shown that Fricke dosimeters in common use cannot

be considered to be “large” detectors and, therefore,‘‘gen-

eral cavity theory” should be applied in converting the

dose to water. It is conﬁrmed that plastic dosimeter vessels

have a negligible wall effect. The wall correction factor

for a 1-mm-thick Pyrex-walled vessel varies with incident

photon energy from 1.001  0.001 for a

Co beam to

0.983  0.001 for a 24-M (  0.80) photon beam.

( is the ratio of absorbed dose at 20-cm depth to

that at 10 cm—‘‘tissue-phantom ratio”). This implies that

previous Fricke measurements with glass-walled vessels

should be re-evaluated.

For high-energy photon (and electron) beams, the

absorbed dose to water averaged over the volume occupied

by a wall-less Fricke dosimeter, D

, can be obtained as

(7.18)

where

f is the absorbed dose conversion factor and D

the dose calculated according to Equation (7.3) for a wall-

less Fricke dosimeter; Equation (7.18) effectively deﬁnes f.

For the case of a non-water-walled vessel with Fricke dose

, one can write

(7.19)

which deﬁnes P

wall

as the ratio of the absorbed dose to the

Fricke solution obtained with a wall-less dosimeter to that

with the non-water-walled dosimeter. Putting Equations

(7.18) and (7.19) together,

is given by

(7.20)

Instead of using two factors in determining the dose

to water, a general conversion factor F

can be used; i.e.,

(7.21)

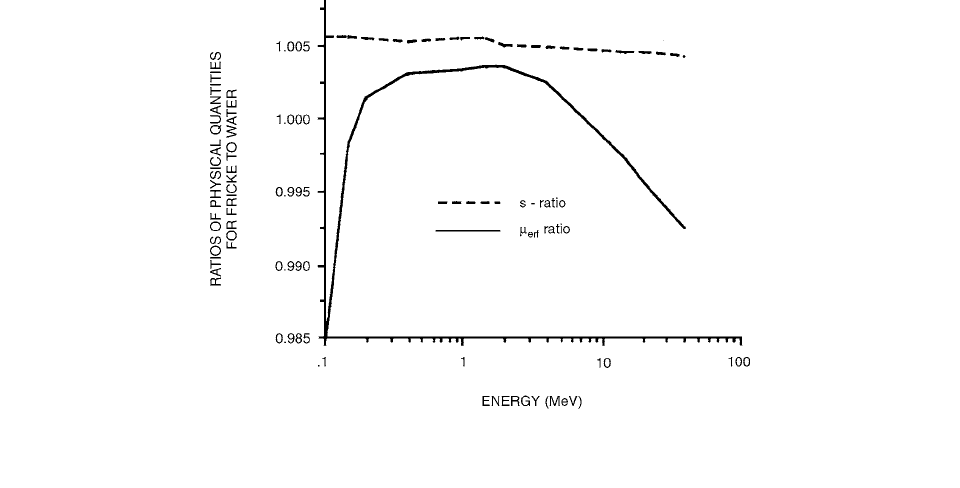
For megavolt photons, the ratio of the mass energy

absorption coefﬁcients for water to the Fricke dosimeter

solution, (







)

water,f

, decreases with increasing photon

energy (see Figure 7.4). The dose conversion factor

derived from general cavity theories should be somewhere

between (







)

water,f

and s

water,f

. The fractional dose result-

ing from the electrons generated by photon interactions

in the dosimeter solution decreases with increasing inci-

dent photon energy (see Figure 7.5).

EGS4 Monte Carlo calculations show for megavoltage

radiotherapy photon beams, and experimental measure-

ments conﬁrm with an accuracy of 0.2%, that glass- or

quartz-walled vials used in Fricke dosimetry increase the

dose in the Fricke solution. [5] This is caused mainly by

increased electron scattering from the glass, which increases

the dose to the Fricke solution. For plastic vials of similar

shapes, calculations demonstrate that the effect is in the

opposite direction, and even at high energies it is much less

(0.2% to 0.5%).

ICRU Report 35 [9] recommended the use of plastic

dosimeter vessels for Fricke dosimetry in the determina-

tion of absorbed dose in a phantom irradiated by high-

energy photon and electron beams. Plastic vessels have

FIGURE 7.4 The photon mass energy absorption coefﬁcients for water to the Fricke dosimeter solution. The dashed line shows the

electron mass stopping power ratio for water to the Fricke dosimeter solution. (From Reference [4]. With permission.)

TPR



D

wall

D



wall

D



wall



CH-07.fm Page 353 Friday, November 10, 2000 12:03 PM

354 Radiation Dosimetry: Instrumentation and Methods

linear attenuation coefﬁcients and stopping-power values

somewhat less than those for water, and this compensates

for the somewhat greater values in the ferrous sulphate

solution. The main purpose of using plastic vessels is to

minimize the perturbation effects on the electron scatter-

ing introduced by the presence of the Fricke dosimeter

in the water phantom. However, a great deal of care is

required with plastic vessels because of storage effects,

i.e., chemical effects on the ferrous sulphate solution when

stored in the plastic container. For glass vessels, the per-

turbation and cavity theory effects are potentially larger.

Burlin and Chan [11] showed both experimentally and

theoretically that the cavity-theory effects could be as

large as 7% with small volumes of Fricke solution in thick-

walled silica vessels in a

Co beam. This is because in

the normal, i.e., large volume detector, one considers the

Fricke solution to be a photon detector in which all the

dose is delivered by electrons starting in the Fricke

solution and, hence, D

med

 D

, where D

med

is the dose to the medium and D

is the dose to the Fricke

solution. In the small volume detector, one has an electron

detector in which the dose is delivered by electrons start-

ing in the walls; hence, Bragg-Gray cavity theory applies

and one has

med

 .

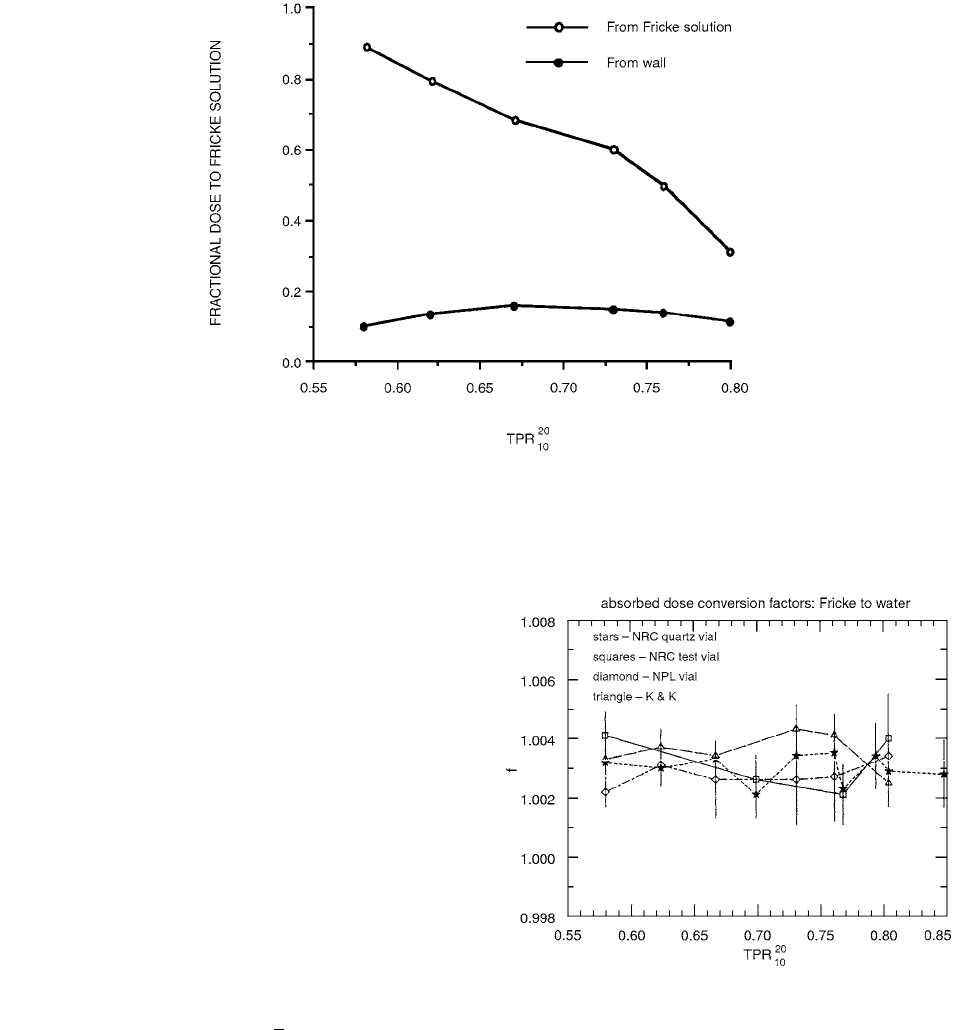
Results for the calculated absorbed-dose conversion

factors relating the absorbed dose in the Fricke solution

to the absorbed dose in the homogeneous water phantom

at the same point are presented in Figure 7.6.

Figure 7.7 presents summaries of the calculated wall-

correction factors

wall

for the standard coin-shaped,

quartz-walled Fricke vials used at NRC. These corrections

are substantial and must be taken into account. To facilitate

their use, these data have been ﬁt to a simple linear expres-

sion in terms of :

(7.22)

FIGURE 7.5 The fractional doses resulting from electrons generated by photon interactions in either the Fricke dosimeter solution or

in the wall material. The remaining contribution is from the medium. The dosimeter is 1.354 cm in diameter and 5.5 cm in length.

The wall material is Pyrex glass and the thickness is 1 mm. (From Reference [4]. With permission.)





()

Fricke

med





()

Fricke

wall





()

wall

med

FIGURE 7.6 Absorbed-dose conversion factors, f, for converting

dose to Fricke solution into dose to water for Fricke vials of

various shapes as described in the text. Stars, NRC standard vial

shape; squares, NRC test vial shape; diamonds, NPL vial shape

with no air gaps; triangles, long circular vial shape to model Kwa

and Kornelsen vials. (From Reference [5]. With permission.)

TPR

wall

1.0478 0.08223 TPR

()

CH-07.fm Page 354 Friday, November 10, 2000 12:03 PM

Chemical Dosimetry 355

The data show an apparent departure from a linear

relationship near  0.76. This may be associated

with the change in the reference depth from 5 to 7 cm at

this point, or it may indicate that is not a good

beam quality indicator for this correction, or it may just be

a statistical ﬂuctuation.

The polyethylene walls reduce the dose to the Fricke

solution.

The NRC vials are made of quartz because they were

designed for use in a calibration service in which the vials

were shipped to the clinic for measurements and hence

must not suffer from chemical storage effects. In view of

the correction factors, it may be more appropriate in-house

to use plastic-walled vials.

If electron transport is not included in the Monte

Carlo calculation, the effect of the front and back wall

is only a 0.27% reduction in dose; i.e., although the front

wall attenuates the primary beam by 0.55%, the addi-

tional dose from photon scatter changes the net effect to

0.27%. [5]

Ma and Nahum [6] presented Fricke-to-water dose

conversion and wall correction factors for Fricke ferrous

sulphate dosimetry in high-energy electron beams. The

dose conversion factor has been calculated as the ratio of

the mean dose in water to the mean dose in the Fricke

solution with a water-walled vessel, and the wall correc-

tion factor accounts for the change in the Fricke dose due

to the presence of the non-water wall material. The results

show that for a Fricke dosimeter of 1.354-cm diameter

and 5.5-cm length, the dose conversion factor is nearly

constant at 1.004 (within 0.1%) for electron energies of

11–25 MeV if the dosimeter is placed at the depth of

maximum dose, but it can vary by a few percent if the

dosimeter is placed on the descending portion of the

depth-dose curve. The wall corrections are smaller than

0.3% for 0.1-cm-thick polystyrene vessels. For 0.1-cm-

thick Pyrex glass vessels, the wall correction factor varies

from 0.989 for 11 MeV at 2.75-cm depth to 0.997 for 25

MeV at 7-cm depth. This conﬁrms recent experimental

ﬁndings that Fricke doses obtained with glass-walled ves-

sels were up to 1% higher than those with polystyrene-

walled vessels.

The wall correction factor p

wall

accounts for any

change in the absorbed dose in the Fricke dosimeter

solution due to the presence of the non-water-equivalent

FIGURE 7.7 Wall-correction factors p

wall

for converting absorbed

dose to Fricke solution measured in the standard quartz-walled vials

and the polyethylene-walled test vials to dose in wall-less detectors.

The dashed line shows the values from Equation (7.22). (From

Reference [5]. With permission.)

TPR

FIGURE 7.8 The Monte Carlo–calculated p

wall

for a Fricke dosimeter of 1.354-cm diameter and 5.5-cm length at a depth of either

d  2.75 cm or d  3.2 cm in water irradiated by monoenergetic electron beams of 10  10 cm

ﬁeld size. The wall thickness is

0.1 cm and the wall material is Pyrex. The Monte Carlo statistical uncertainties are shown as error bars on the curves. (From Reference

[6]. With permission.)

CH-07.fm Page 355 Friday, November 10, 2000 12:03 PM

356 Radiation Dosimetry: Instrumentation and Methods

wall material. The perturbation of the electron ﬂuence

in the phantom by the non-water-equivalent wall

depends on the combined effect of the difference in mass

stopping power, scattering power, and density between

the wall and phantom material. For a Pyrex glass wall,

for instance, the mass stopping power is lower than that

of water, but it has a much greater density (2.23 g cm

3

)

and scattering power compared to water. The glass-wall

effect will therefore mainly result from the high density

and scattering power of the wall material. On the other

hand, plastic wall materials such as polystyrene gener-

ally have smaller stopping powers and/or scattering

powers and hence may cause effects in the opposite

direction.

It is seen in Figure 7.8 that the high density of the

Pyrex glass causes more rapid fall-off of the dose with

depth and therefore reduces the dose in the Fricke dosim-

eter solution.

Aqueous coumarin was investigated by Collins et al

[7] as a possible dosimeter for radiation therapy appli-

cations. Coumarin-3-carboxylic acid in aqueous solu-

tions converts, upon irradiation, to the highly ﬂuorescent

7-hydroxy-coumarin-3-carboxylic acid. The intensity of

the ﬂuorescence signal is linearly proportional to the num-

ber of the formed 7-hydroxy-coumarin-3-carboxylic acid

molecules, which in turn is proportional to the radiation-

absorbed dose. The system exhibits nearly linear behavior

with dose, in the range of 0.1 to 50 Gy.

Concentrations in the range of 10

3

to 10

5

M were

prepared by diluting the appropriate amount of coumarin

in distilled water and heating the solution. Buffer (PBS

pH 7.4) was added at the end. The 7-hydroxy-coumarin-

3-carboxylic acid is easily soluble in water and heating

was not necessary.

Coumarin solutions were irradiated in polystyrene

or polymethylmethacrylate (PMMA) 1-cm-path-length

cuvettes (4.5-ml volume, 1-mm wall thickness) at room

temperature with either a

137

Cs gamma-ray source (dose

rate approximately 1 Gy/min) or a Varian Clinac 2100C

linear accelerator (nominal dose rates 0.8, 1.6, 2.4, and

4 Gy/min) in air or water. The absorption spectra of cou-

marin (10

4

M), 7-hydroxy-coumarin (10

4

M), and irra-

diated coumarin (10

4

M, dose of 250 Gy) are shown in

Figure 7.9.

Fluorescence spectra of 7-hydroxy-coumarin (10

7

M),

coumarin (10

4

M) and irradiated solution of coumarin

(10

4

M, dose of 10 Gy) are shown in Figure 7.10 in the

range of 350 to 600 nm. The 7-hydroxy-coumarin and the

irradiated coumarin spectra were generated under 388-nm

excitation. The coumarin emission was excited with 330 nm

(coumarin excited at 388-nm shows negligible ﬂuores-

cence). The spectra of the 7-hydroxy-coumarin and the irra-

diated coumarin exhibit the same emission peak centered

at 450 nm. The un-irradiated coumarin solution exhibits

a weak luminescence maximum at 410 nm. Both the 450-

nm emission band in hydroxy-coumarin and the 410-nm

FIGURE 7.9 Room-temperature absorption spectra of coumarin-3-carboxyl acid (10

4

M), 7-hydroxy-coumarin-3-carboxyl acid

(10

4

M), and coumarin-3-carboxyl acid (10

4

M) irradiated with 250 Gy. (From Reference [7]. With permission.)

CH-07.fm Page 356 Friday, November 10, 2000 12:03 PM

Chemical Dosimetry 357

band in coumarin are assigned to a transition from the

triplet



state to the ground state. [7]

Figure 7.11 depicts the ﬂuorescence of 10

4

coumarin solution irradiated in air with a linear accel-

erator 6-MV pulsed photon beam at a nominal dose

rate of 4 Gy/min in the dose range of 0 to 300 Gy.

The solution was irradiated and measured in PMMA con-

tainers with a volume of 3 ml. The measured signal was

compared to the signal of a standard solution of 10

7

7-hydroxy-coumarin.

Gupta et al. [8] gave the absorption spectra of the ferric-

xylenol orange complex and discussed the effect of acidity

on the absorption maxima in the presence of alanine,

glutamine, and valine. The irradiated alanine and glutamine

were read by ﬁve different methods:

1. Amino acid dissolved in 9.8 mL of aerated sul-

phuric acid. 0.1 mL each of xylenol orange and

ferrous ions were added one after the other.

2. Amino acid dissolved in 9.8 mL of aerated sul-

phuric acid. Then 0.1 mL each of ferrous ions

and xylenol orange were added one after the

other; xylenol orange was added after the reac-

tion with ferrous ions was over.

3. Amino acid dissolved in 10 mL of aerated FX

solution.

FIGURE 7.10 Room-temperature ﬂuorescence of coumarin-3-carboxyl acid (10

7

M) and coumarin-3-carboxyl acid (10

4

M) irra-

diated with 10 Gy. (From Reference [7]. With permission.)

FIGURE 7.11 Fluorescence of irradiated 10

4

M aqueous coumarin-3-carboxylic acid vs. radiation-absorbed dose. The excitation

was at 400 nm, the emission at 450 nm, and the resolution at 5 nm. (From Reference [7]. With permission.)

CH-07.fm Page 357 Friday, November 10, 2000 12:03 PM

358 Radiation Dosimetry: Instrumentation and Methods

4. Amino acid dissolved in 9.8 or 9.9 mL of aer-

ated ferrous sulphate solution, and 0.2 or 0.1

mL of 0.01 mmol dm

3

xylenol orange was

added later.

5. Amino acid was dissolved in 9.8 or 9.9 mL of

oxygenated ferrous sulphate solution, and 0.2

or 0.1 mL of 0.01 mmol xylenol orange

was added later.

Figures 7.12 and 7.13 show that the oxidation of fer-

rous ions for method 3 is almost double that for

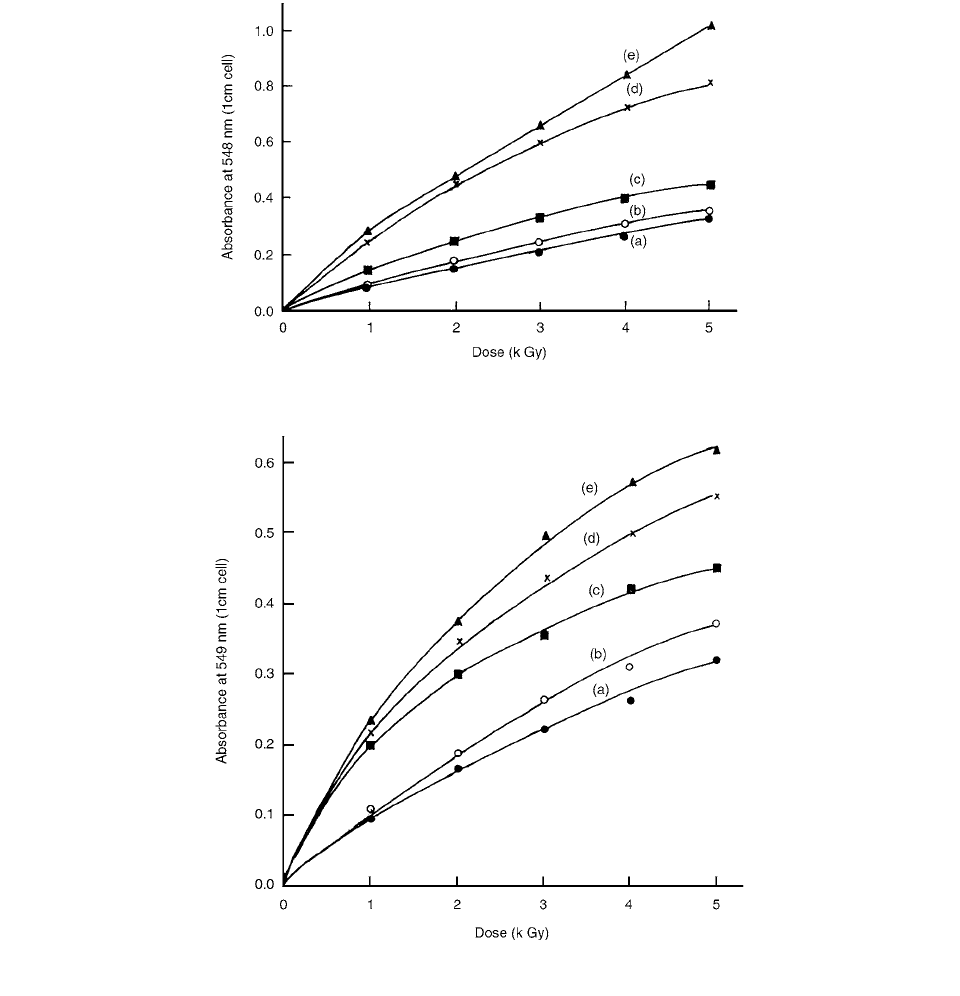
method 1. The oxidation increases further for methods

(4) and (5).

Glutamine powder was irradiated to 50-kGy and 5-

kGy doses. Twenty mg of irradiated powder was dis-

solved in 5 mL of 0.033 mol dm

3

aerated sulphuric

acid and 5mL of FX solution containing 0.4 mmol dm

3

of ferrous ammonium sulphate; 0.2 mmol dm

3

of xyle-

nol orange in 0.033 mol dm

3

sulphuric acid was added

later (method b). Ten measurements were done using

methods (3) and (6). Figure 7.14 shows the oxidation

of ferrous ions by the two methods for valine. [8]

FIGURE 7.12 Oxidation of ferrous ions by irradiated alanine. (From Reference [8]. With permission.)

FIGURE 7.13 Oxidation of ferrous ions by irradiated glutamine. (From Reference [8]. With permission.)

3

CH-07.fm Page 358 Friday, November 10, 2000 12:03 PM

Chemical Dosimetry 359

The oxidation of ferrous ions by the dissolution of

amino acids in aqueous aerated acidic solution can be

written as follows:

where and are two free radicals formed on the

radiolysis of amino acids. There is a competition between

reactions (1) and (2). Here R

is a stable product. Some

free radicals oxidize ferrous ions directly. This competition

kinetics gives the following relationship:

(7.23)

where

A is the absorbance of the ferric-xylenol orange

complex in the presence of the amino acid, D is the dose,

and C

are constants.

REFERENCES

1. Xu, Z. et al., Med. Phys., 23, 377, 1996.

Hazle, J. D. et al., Phys. Med. Biol., 36, 1117, 1991.

Chauvenet, B. et al., Phys. Med. Biol., 42, 2053, 1997.

Ma, C-M. and Nahum, A. E., Phys. Med. Biol., 38, 93,

1993.

Ma, C-M. et al., Med. Phys., 20, 283, 1993.

Ma, C-M. and Nahum, A. E., Phys. Med. Biol., 38,

423, 1993.

Collins, A. K. et al., Med. Phys., 21, 1741, 1994.

Gupta, B. L. et al., in Proc. High Dose Dosimetry for

Radiation Protection,

IAEA, 1991, 327.

ICRU 35, Radiation dosimetry: electron beam with

energy 1–50 MEV, 1984.

10.

Burlin, T. E., Br. J. Radiol., 39, 727, 1966.

11.

Burlin, T. E. and Chan, F. K., Int. J. Appl. Radiat. Isot.,

20, 767, 1969.

FIGURE 7.14 Oxidation of ferrous ions by irradiated valine (methods 3 and 6). (From Reference [8]. with permission.)

 R



HFe

 R



HFe

 products Fe



 Fe

products

1/ A[] C

/ D[] C



CH-07.fm Page 359 Friday, November 10, 2000 12:03 PM