Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

3.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

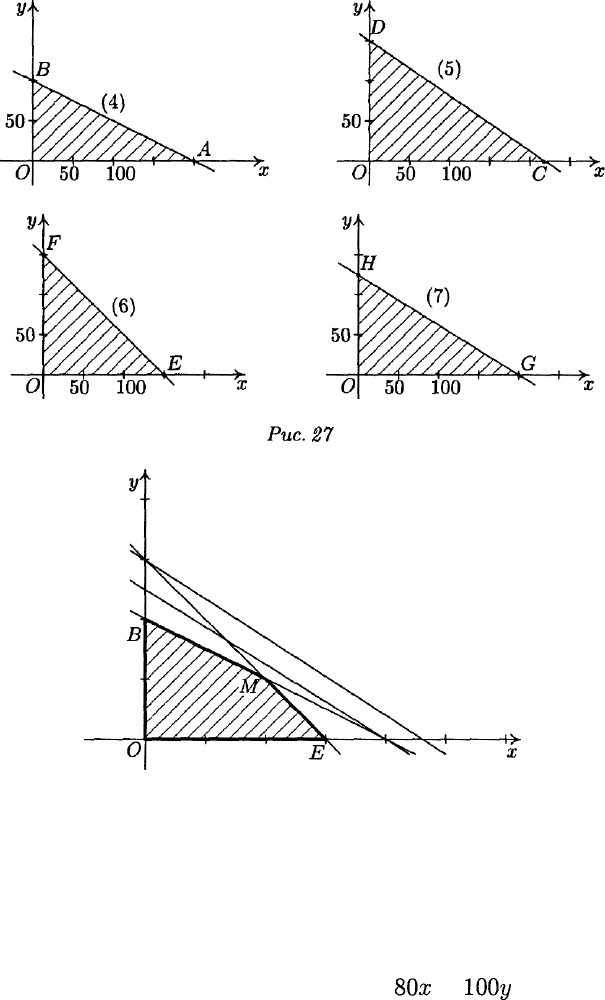
Рис.

Рис. 28

а затем, используя точку начала отсчета 0(0,0), определить соот-

ветствующие полуплоскости (рис. 27).

Пересечением полученных полуплоскостей будет четырех-

угольник, изображенный на рис. 28.

Напомним, что линейная функция z =

80a;

100у

достигает наи-

большего значения в одной из вершин этого четырехугольника. По-

этому для ответа на поставленный вопрос необходимо

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

3.2.3. Общая задача линейного программирования

В общем случае и число неизвестных, и число ограничений могут

достигать десятков, сотен, тысяч и т. д. Однако набор соответству-

ющих условий ничем (кроме количества) от рассмотренных выше

примеров не отличается. Это нетрудно заметить уже по общей по-

становке задачи линейного программирования.

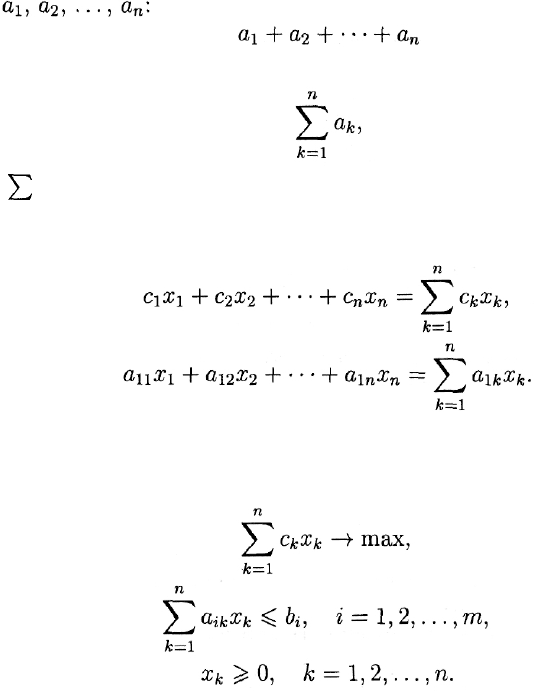
Стандартная математическая формулировка общей задачи ли-

нейного программирования выглядит так:

требуется найти экстремальное значение показателя эффектив-

ности (целевой функции)

(линейной функции элементов решения

Х\,

...,

)

при линейных

ограничительных условиях, накладываемых на элементы решения:

1) найти координаты точки пересечения прямых (4) и (6) — точки

М (координаты вершин В и Е известны):

решая систему уравнений

находим значения х и

у:

х = 100, у = 50;

2) вычислить значения z в точках

В(0,100),

£'(150,

0),

М(100,

50):

3) выбрать наибольшее:

Ответ:

3.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Что касается существующих методов решения этой задачи с чи-

слом переменных, большим двух, то в их основе лежат те же идеи,

на которые мы опирались при разработке графического подхода.

Конечно, в случае сильного увеличения числа переменных и огра-

ничений техника получения решения заметно усложняется, но она

опирается на совершенно стандартные, хорошо разработанные ал-

горитмы (возникающие трудности связаны лишь с ростом объема

необходимых вычислений).

Общую постановку задачи линейного программирования можно

записать в более компактной форме, если воспользоваться следую-

щим правилом.

А вот как выглядит запись общей задачи линейного программи-

рования:

где

— знак суммирования, а к — индекс суммирования.

Это обозначение очень удобно:

принята такая запись:

Правило сокращенного суммирования. Для обозначения суммы чи-

сел

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

3.2.4. Транспортная задача

Важный тип задач линейного программирования представляет зада-

ча о перевозках. Называется она так потому, что цель этой задачи

заключается в минимизации полной стоимости перевозок известного

количества товаров со складов к потребителю.

Мы поговорим здесь о так называемой сбалансированной транс-

портной задаче — задаче о перевозках, в которой общий объем то-

варов, готовых к отправлению, в точности равен объему товаров,

который готовы принять в пунктах назначения.

Пример 9. Компания имеет два товарных склада и трех опто-

вых покупателей. Известно, что общий объем запасов на складах

составляет 300 тыс. единиц продукции и совпадает с общим объемом

заказов покупателей.

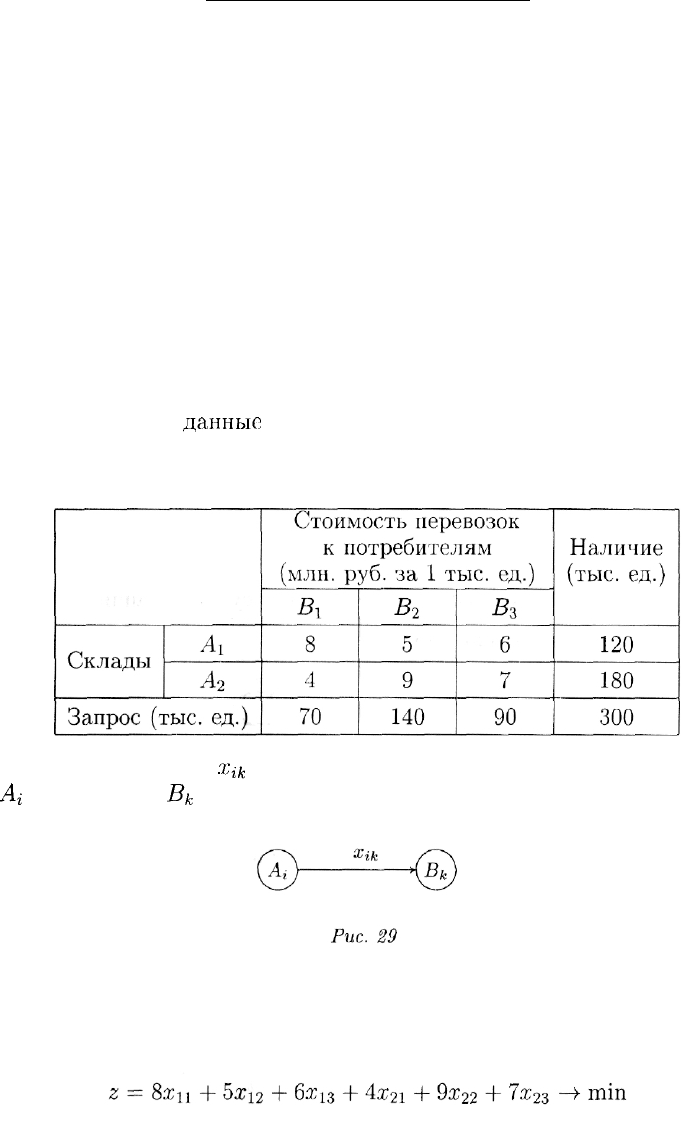
Конкретные

данные

о загруженности каждого из складов

(в тыс. ед.), потребности каждого покупателя (в тыс. ед.) и стоимо-

сти перевозки (млн. руб. за 1 тыс. ед.) приведены в таблице:

Обозначим через

%tu

количество товара, поставляемого со склада

покупателю

(рис. 29).

Тогда соответствующая транспортная задача может быть сфор-

мулирована следующим образом.

Минимизировать общую стоимость перевозок:

3.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

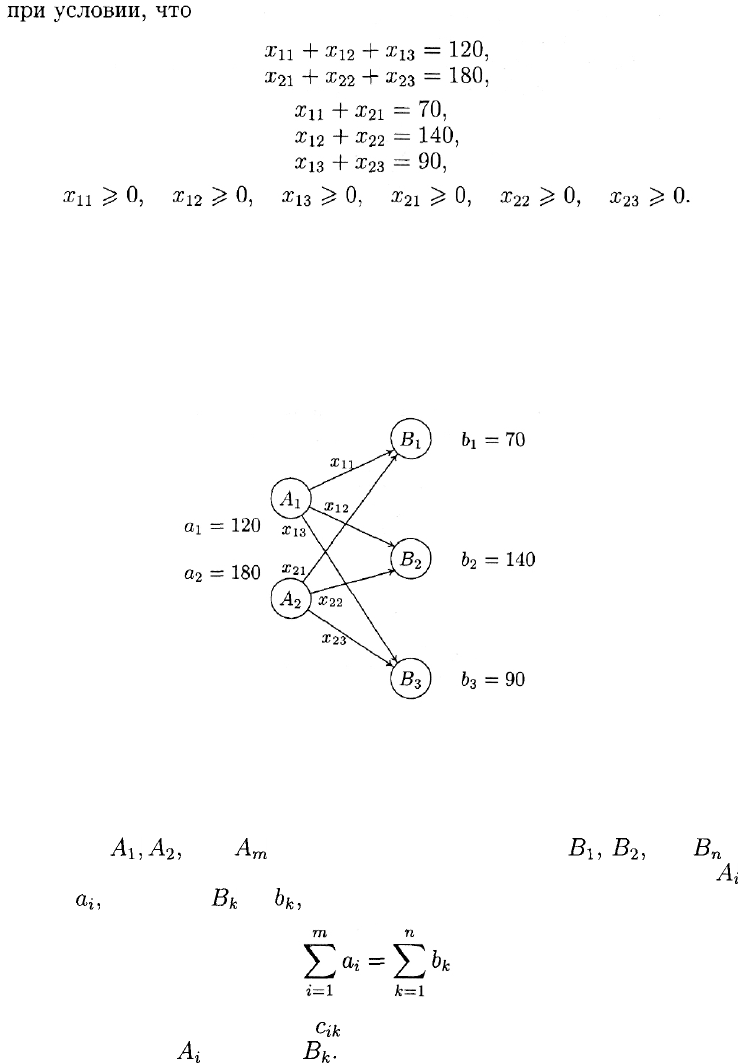
Получаем задачу линейного программирования, в которой основ-

ные ограничения вследствие того, что транспортная задача сбалан-

сирована, являются равенствами.

Замечание. Для лучшего понимания поставленной задачи часто по-

лезно воспользоваться сетью (рис. 30).

Рис. 30

Перейдем теперь к общей постановке сбалансированной транс-

портной задачи.

Пусть

А\, А

...,

— пункты отправления, а

В\, В

...,

—

пункты назначения. Известно, что число единиц товара в пункте

А{

равно

в пункте

—

bh,

причем

(задача сбалансирована), и

Qfc

— стоимость перевозки единицы то-

вара из пункта

в пункт

В^.

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

Обозначим через

ХЦ.

(искомое) число единиц товара, пересылае-

мого из пункта

в пункт

В^.

Тогда общее количество товара, которое можно отправить из

пункта

в пункты

, В

• •.,

равно

— общее количество товара, которое можно принять в пункте

из

пунктов

...,

Стоимость перевозки

х&

единиц товара из пункта

А(

в пункт

равна

CikXik,

а общая стоимость всех перевозок —

В результате мы получаем следующую задачу линейного про-

граммирования:

все

Xik^

Покажем, как в некоторых простых случаях транспортную зада-

чу можно решать графическим методом.

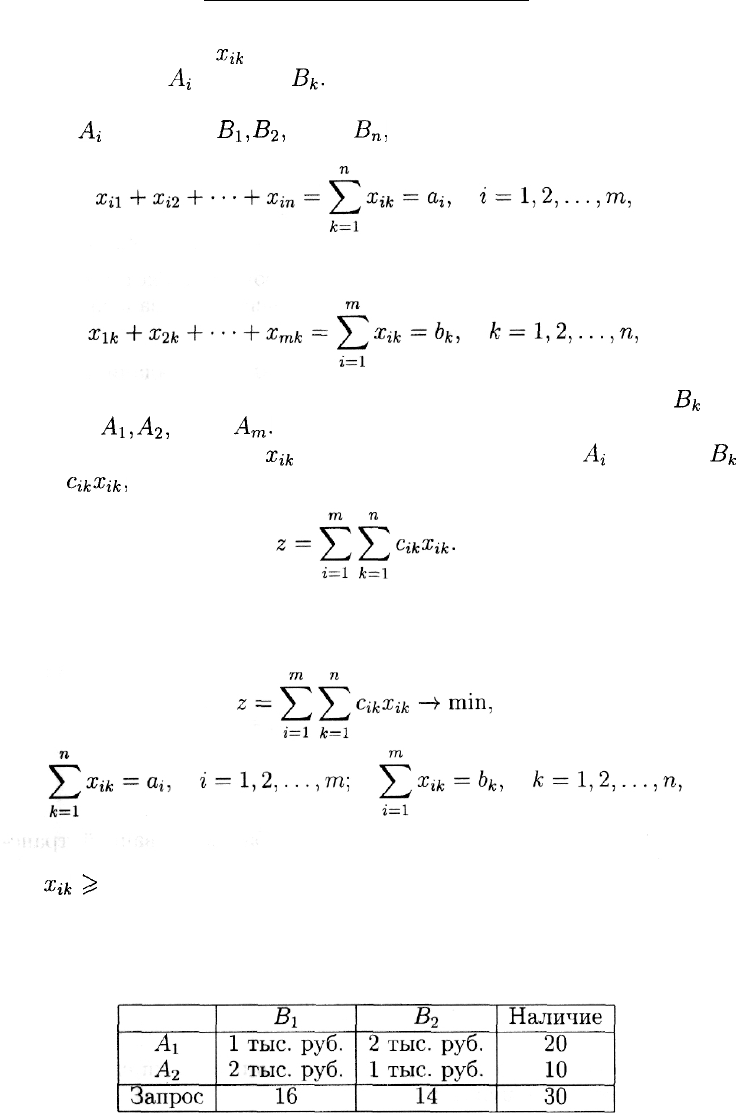
Пример 10. Рассмотрим транспортную задачу, заданную таб-

лицей

3.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Решение. Пусть

Xik

— искомое число единиц товара, пересылае-

мого из пункта

в пункт

В^.

Тогда данные таблицы можно пред-

ставить в следующем виде:

Рис. 31 Рис. 32 Рис. 33

На плоскости Otz уравнение z — 66 —

изображается прямой

(рис. 32). Из того, что все

Xik

неотрицательны, получаем, что пере-

менная t должна удовлетворять одновременно следующим четырем

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

3.2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

которую можно решить графическим методом.

Выписанные неравенства определяют на плоскости (и, v) пяти-

угольник с вершинами

(30,0), (70,0), (70,50), (0,120), (0,30).

Нетрудно убедиться в том, что z =

= 1690 при

= 0, v = 120.

Ответ:

= 0,

г2

= 120,

= 0,

= 70,

= 20,

90,

min

= 1690.

3.2.5. Целочисленное линейное программирование

Если переменные в задаче линейного программирования соответс-

твуют числу машин, станков, людей или каких-либо иных недели-

момых объектов, то имеют смысл только целочисленные (целые)

значения этих переменных.

Рассмотрим следующий пример.

Пример 11. Найти решение задачи

z = Их — у

—>

max,

Юх-у

40,

х + у

20,5,

0, у

ограничиваясь целочисленными значениями переменных х и у.

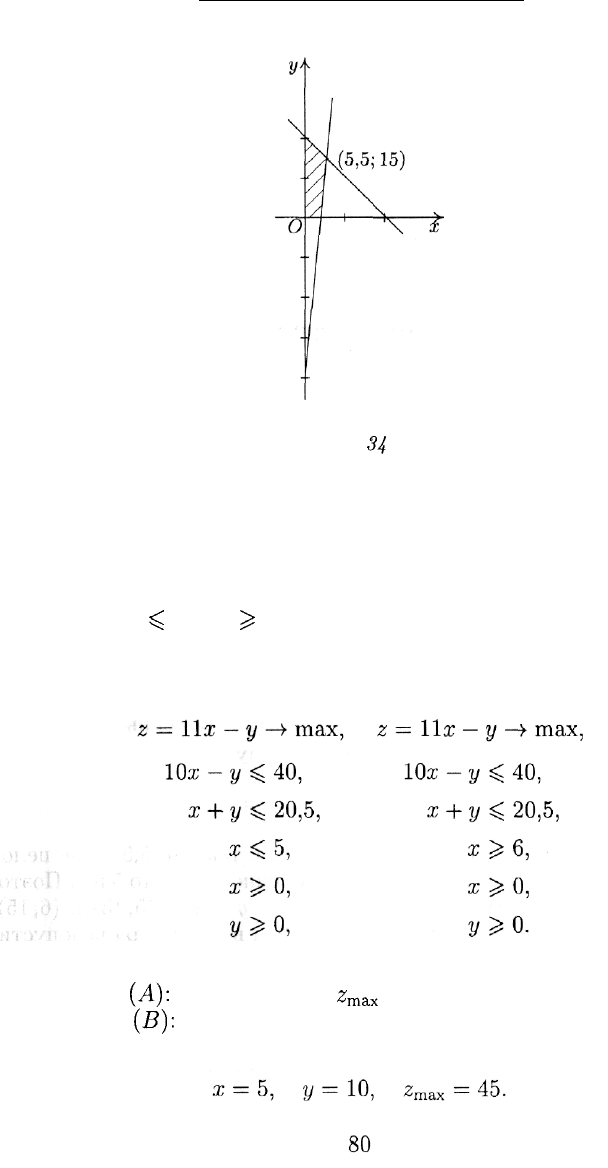
Решая задачу графическим методом, получаем

х = 5,5, у = 15, z

max

= 45,5

(рис. 34). Однако это решение недопустимо, так как 5,5 — не целое

число. Ближайшие целые значения переменной х — это 5 и 6. Поэто-

му кажется разумным рассмотреть для

(х,

у) пары (5,15) и (6,15).

Первая пара приводит к значению z = 40, а вторая пара недопусти-

ма: не удовлетворяет первым двум неравенствам задачи.

Однако, исследуя ситуацию графически, нетрудно показать, что,

ограничиваясь только целочисленными значениями переменных,

можно получить для величины z значение, большее 40. В самом де-

ле, пара (5, 10) приводит к z = 45, и это действительно оптимальное

решение задачи.

ГЛАВА 3. ЛИНЕЙНЫЕ ЗАДАЧИ

Рис.

Покажем, как его можно получить. Для того чтобы найти воз-

можные целые значения переменных х и у, исходная задача разби-

вается на две подзадачи, выбирается переменная с нецелочисленным

значением, в данном случае переменная х, вводятся два новых ог-

раничения: х ^ 5 и х ^ 6, где 5 и 6 — целые числа, ближайшие к

5,5, и рассматриваются две новые задачи:

(А)

(В)

Решая обе задачи графическим методом (рис. 35), получаем, что

подзадача

(А):

х — 5, у = 10,

max

= 45;

подзадача

(В):

решения не имеет (противоречивые условия).

Целочисленное решение подзадачи (А) и дает искомый ответ: