Шивринский В.Н. (под редак.) Проектирование приборов, систем и измерительно-вычислительных комплексов
Подождите немного. Документ загружается.

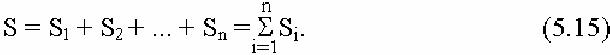
41
В установившемся режиме измерения
M
вр
= M
пр
. (5.10)
Решая совместно (5.8-5.10), получим
mal = C
пр
ϕ,
ϕ = mla/C
пр
= 12mlLa/(bh
3
E),
U
вых
= 12mlLU
o
a/(ϕ
o
bh
3
E). (5.11)
Уравнение (5.11) может быть получено непосредственно по структурной
схеме прибора (рис. 5.3), для этого необходимо определить передаточные ко-
эффициенты звеньев (1-4):
K
1
= ∂F/∂a = m; K
2
= l; K
3
= ∂ϕ/∂M = 1/C
пр
; K
4
= ∂U/∂ϕ = U
o
/ϕ
o
.
Учитывая, что U
вых
= Ka, где K = K
1
K
2
K
3
K
4
, получим статическую характе-
ристику акселерометра в виде (5.11).
Параллельное соединение (рис. 4.1, б). Если характеристики n параллельных
звеньев имеют вид
У
1
= f
1
(X);
У
2
= f
2
(Х);
. . . . . . . .
У
n
= f
n
(Х), (5.12)
а уравнение связи
У = У
1
+ У
2
+ ... + У
n
, (5.13)
то статическая характеристика системы получается подстановкой уравнений
(5.12) в уравнение связи (5.13):
У = f
1
(X) + f
2
(Х) + ... + f
n
(Х). (5.14)
Для определения чувствительности дифференцируем уравнение (5.14) по
входной величине Х:
S = ∂У
1
/∂X + ∂У
2
/∂Х + ... + ∂У
n
/∂Х.
Имея в виду, что
∂У
1
/∂X = S
1
, ∂У
2
/∂Х = S
2
, ..., ∂У
n
/∂Х = S
n
,
получим
При графическом расчете характеристики всех параллельных звеньев стро-
ят в прямоугольной системе координат (в I-й четверти). Суммируя ординаты
всех кривых при фиксированном значении Х, находят координаты точек ре-
зультирующей характеристики.
Встречно-параллельное соединение (рис. 4.1, в). Если характеристики двух
встречно-параллельных звеньев имеют вид
У = f
1
(X
1
);
Х
2
= f
2
(У), (5.16)
то, решая их совместно с уравнением связи
Х
1
= X ± Х
2
,
42
получим в неявном виде характеристику системы:
У = f
1
[X ± f
2
(У)]. (5.17)
В полученном уравнении знак «плюс» отвечает положительной обратной
связи, знак «минус» – отрицательной.
Чувствительность системы при встречно-параллельном соединении звеньев
определяется как
S = S
1
/(1±S
1
S
2
). (5.18)
Здесь знак «плюс» отвечает отрицательной обратной связи, знак «минус» –
положительной.
При графическом расчете характеристики обоих звеньев строят в прямо-
угольной системе координат (в I-й четверти). Суммируя абсциссы этих кривых
при фиксированном значении У, находят координаты точек результирующей
характеристики.
Методы расчета динамических характеристик
При расчете динамических характеристик приборов могут решаться задачи
анализа и синтеза.
Анализ динамических характеристик ведется с целью определения характе-
ра изменения выходного сигнала прибора во времени У(t) при известном законе
изменения входного сигнала Х(t) и при заданных параметрах прибора.
Задача синтеза заключается в выборе таких параметров прибора, при кото-
рых зависимость У(t) наилучшим образом приближается к желаемой.
Зависимость У(t) называют реакцией прибора на воздействие Х(t). Если бы
прибор был идеальным в динамическом отношении (безынерционным), то его
выходной сигнал реагировал бы без запаздывания на изменение входного сиг-
нала и воспроизводился бы в соответствии со статической характеристикой
У = f(Х), т. е.
У(t) = f[Х(t)]. (5.19)
В реальных приборах (вследствие наличия инерционных масс, демпфиро-
вания, тепловой инерции, емкостей и индуктивностей в электрических цепях и
т. п.) условие (5.19) не выполняется и возникает динамическая погрешность
∆У
дин
= У(t) – f[Х(t)]. (5.20)
В общем случае для расчетного определения У(t) необходимо два уравне-
ния, одно из которых выражает закон изменения Х:
Х = Х(t), (5.21)
а другое отображает физическую схему прибора и дает связь между У, Х и их
производными:
f
1
[У
(n)
, У
(n-1)
, ..., У] = f
2
[Х
(m)
, Х
(m-1)
, ..., Х], (5.22)
здесь У
(n)
= d
n
У/dt
n
; Х
(m)
= d
m
Х/dt
m
.
Совместное решение и интегрирование уравнений (5.21) и (5.22) позволяет
определить реакцию прибора У(t) на воздействие Х(t) при заданных начальных
условиях, учитывающих состояние координаты У и ее производных в момент
времени t = 0.
43
Число начальных условий равно порядку левой части уравнения (5.22). Та-
ким образом, реакция прибора У(t) зависит как от внешнего воздействия Х(t),
так и от собственных свойств прибора, определяемых уравнением (5.22).
Следовательно, один и тот же прибор обладает различной реакцией У(t) на
разные воздействия Х(t). Закон изменения Х(t) в условиях реальной эксплуата-
ции прибора может быть самым различным и содержать как детерминирован-
ную, так и случайную составляющие.
В целях унификации оценок и возможности сравнения динамических
свойств различных приборов при расчетах и экспериментах принято оценивать
динамические характеристики приборов при типовых воздействиях – ступенча-
том, импульсном, синусоидальном.
Реакцию прибора на ступенчатое воздействие называют переходной функ-
цией, а на импульсное – импульсной переходной функцией. При определении
реакции на синусоидальное воздействие обычно рассматривают только вынуж-
денную составляющую колебаний выходного сигнала, которую представляют в
виде частотных характеристик.
Чаще всего пользуются амплитудно- и фазочастотными характеристиками,
показывающими зависимость амплитуды и сдвига фаз выходного сигнала от
частоты при постоянной амплитуде входного сигнала.
Дифференциальные уравнения (5.22) многих приборов являются линейны-
ми или линеаризуемыми и приводятся к виду
a
0
У
(n)
+a
1
У
(n-1)
+...+a
n
У = b
0
Х
(m)
+b
1
Х
(m-1)
+...+b
m
Х. (5.23)
Совместное решение и интегрирование уравнений (5.21) и (5.23) позволяет
определить У(t). Другой способ нахождения У(t) для приборов, описываемых
линейным дифференциальным уравнением (5.23), основан на применении пре-
образования Лапласа. При этом определяется передаточная функция прибора,
равная отношению лапласовских изображений У(p) и Х(p) при нулевых на-
чальных условиях:
W(p) = У(p)/Х(p) =
= (b
0
p
m
+ b
1
p
m-1
+...+ b
m
)/(a
0
p
n
+ a
1
p
n-1
+...+ a
n
). (5.24)
Определяется лапласовское изображение выходного сигнала в виде
У(p) = W(p)Х(p),
здесь Х(p) – изображение функции Х(t).
Затем находят искомую реакцию
У(t) = L
-1
{У(p)} = L
-1
{W(p)Х(p)},
здесь L
-1
– обратное изображение функции.
В качестве примера рассмотрим движение подвижной части магнитоэлек-
трического измерительного механизма (гальванометра), схема которого приве-
дена на рис. 5.4, где приняты следующие обозначения: 1 – рамка, с ней связан
указатель (стрелка); 2 – постоянный магнит с полюсными наконечниками;
3 – сердечник; 4 – ось (керн); 5 – подпятник; 6 – противодействующие (токо-
подводящие) пружины.
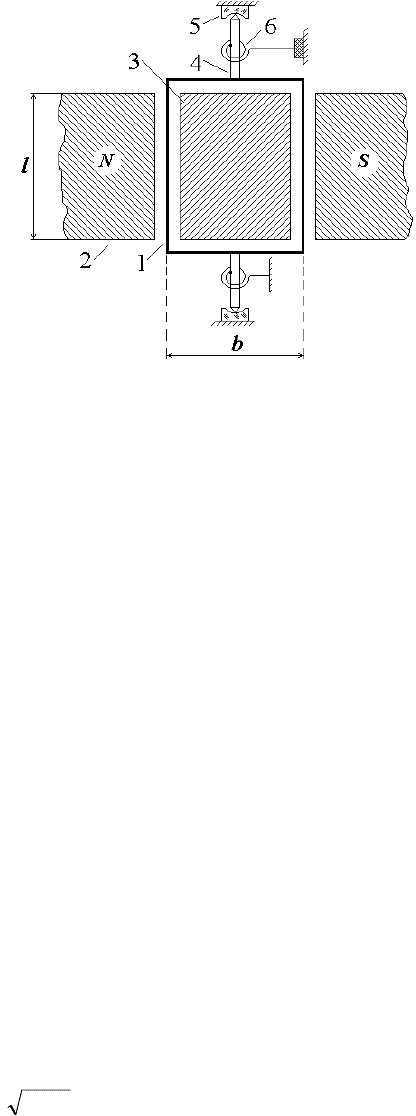
44
Рис. 5.4. Схема магнитоэлектрического механизма
Для рассматриваемой схемы механизма уравнение моментов сил имеет вид
M
и
+ M
д
+ M
п
= M
вр
, (5.25)
здесь M
и
– момент количества движения (инерционный момент); M
д
– демпфи-
рующий момент (момент успокоения); M
п
– позиционный момент (противодей-
ствующий момент); M
вр
– вращающий момент.
Моменты можно выразить через соответствующие коэффициенты:
M
и
= Jϕ''; M
д
= Kϕ'; M
п
= Cϕ; M
вр
= BSWI. (5.26)
Здесь ϕ – угол отклонения подвижной части от состояния равновесия; ϕ', ϕ'' –
первая и вторая производные; J – момент инерции подвижной системы; K – ко-
эффициент демпфирования; C – суммарная жесткость противодействующих
пружин; B – магнитная индукция в воздушном зазоре; W – число витков рамки;
S – активная площадь рамки (S = bl, b – ширина, l – длина активной стороны
рамки); I – ток, протекающий через рамку.
Подставляя (5.26) в (5.25), получим дифференциальное уравнение прибора
Jϕ'' + Kϕ' + Cϕ = BSWI. (5.27)
Характеристическое уравнение
Jp
2
+ Kp + C = 0
можно записать в виде
p
2
+ 2αp + ω
2
o
= 0, (5.28)
здесь α = K/2J; ω
o
=
JC /
.
Параметр ω
o
имеет определенный физический смысл – он определяет кру-
говую частоту собственных недемпфированных колебаний системы.
Для электромагнитного успокоения, при отсутствии металлического корпу-
са рамки, имеем
K = (BSW)
2
/(R
из
+ R
н
), (5.29)
здесь R
из
– сопротивление рамки измерительного механизма; R
н
– сопротивле-
ние внешней цепи (наружное).
В установившемся режиме производные ϕ'', ϕ' равны нулю, тогда
ϕ
уст
= (BSW/C)⋅I. (5.30)
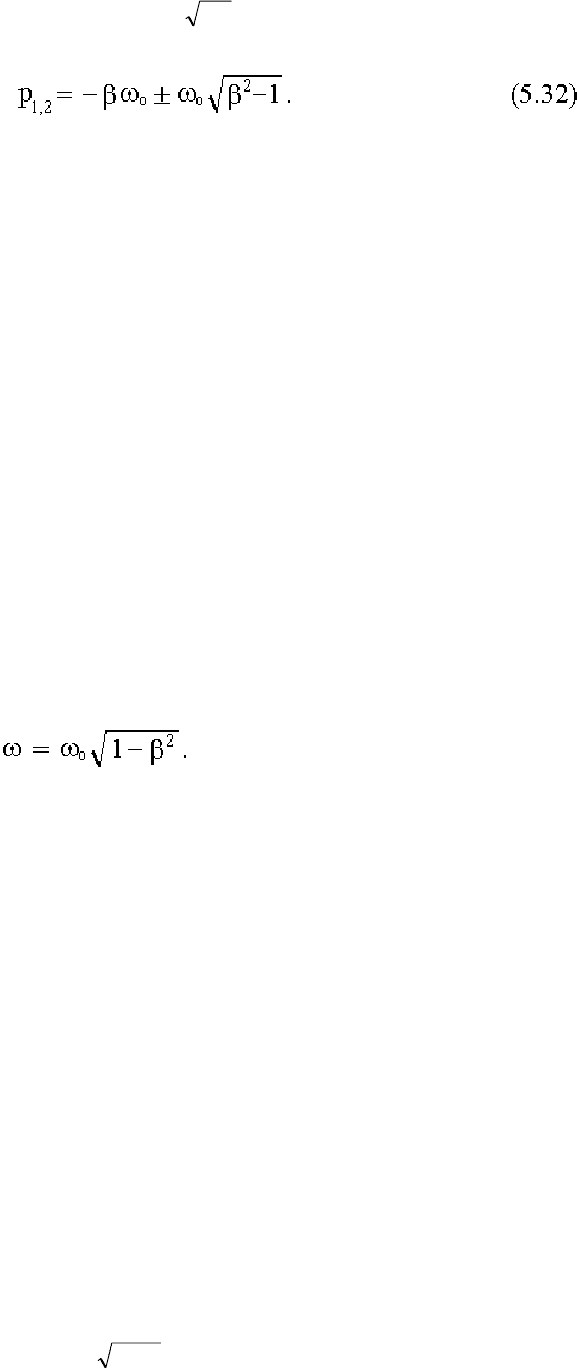
45
Введем безразмерный параметр, называемый степенью успокоения под-
вижной части прибора β:
β = α/ω
o
= K/2 CJ . (5.31)
Корни уравнения (5.28) определим из выражения
Вид переходного процесса зависит от характера корней p
1,2
. Здесь могут
быть три случая.
Случай 1. Степень успокоения β
>1, что приводит к неравным действитель-
ным корням. Переходный процесс в системе 2-го порядка при β
>1 и при нуле-
вых начальных условиях имеет апериодический характер (рис. 5.5).
Случай 2. Степень успокоения β
=1, чему отвечают равные корни. Пере-
ходный процесс является апериодическим.
Случай 3. Корни неравные и комплексные. Этот случай, отвечающий β
<1,
представляет наибольший интерес, так как в этой области существует некото-
рое оптимальное значение β, при котором длительность переходного процесса
получается минимальной.
Переходные процессы при β
<1 имеют колебательный характер. В частном
случае, когда отсутствует демпфирование (β
=
0), система совершает незату-
хающие колебания (при отсутствии сил трения) по закону
ϕ(t) = (BSW/C)(1 – cosω
o
t). (5.33)
Параметр ω
o
представляет собой частоту собственных колебаний недемп-
фированной системы. В случае 0
<β
<1 система совершает затухающие колеба-
ния (рис. 5.5). Частота демпфированных колебаний
Следовательно, с увеличением β от 0 до 1 частота демпфированных коле-
баний уменьшается от ω
o
до 0.
Помимо ω
o
и β, важными показателями колебательного переходного про-
цесса являются декремент затухания и перерегулирование. Декрементом зату-
хания d называют отношение абсолютных значений двух смежных максималь-
ных отклонений выходного сигнала от установившегося значения. Перерегули-
рование σ определяет относительную величину разности между первым макси-
мумом переходного процесса и его установившимся значением.
На рис. 5.5 представлены графики переходных процессов в системе второго
порядка при разных значениях степени успокоения β: β
<1 – колебательный ре-
жим, β
>1 – апериодический режим, β
=1 – критический режим. Изменяя сопро-
тивление цепи прибора (см. уравнение 5.29), можно получить различные режи-
мы его работы.
Опыт показывает, что при степени успокоения β
=
0.9 подвижная часть бы-
стрее всего устанавливается в положение равновесия. Если цепь гальванометра
разомкнута, то колебания рамки будут незатухающими (свободными). Период
собственных колебаний определяется по формуле (5.34).
T
O
= 2π
CJ /
. (5.34)
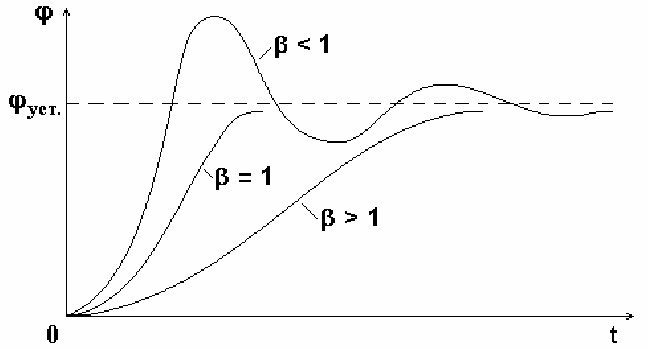
46
Рис. 5.5. График движения подвижной части
гальванометра при разных режимах
Методы расчета динамических характеристик звеньев и систем достаточно
подробно рассматриваются в курсах «Теория автоматического управления и ре-
гулирования» и «Системы автоматического управления».
Оптимизация параметров приборов и систем
Задачи синтеза динамических характеристик приборов и систем весьма
многообразны. Все они преследуют одинаковую цель, заключающуюся в соз-
дании измерительной системы, динамические характеристики которой наилуч-
шим образом приближаются к заданным. Наилучшее приближение достигается
обычно путем оптимизации некоторого заранее выбранного показателя дина-
мического качества.
При проектировании оптимальных по быстродействию или по динамиче-
ской точности измерительных систем могут выбираться различные критерии.
Возможно, например, решение следующих задач синтеза: минимизация дли-
тельности переходного процесса, максимизация полосы пропускания частот,
минимизация фазовых искажений, минимизация дисперсии динамической по-
грешности при действии случайного полезного сигнала и случайной помехи и
т. д. Для повышения быстродействия измерительной системы используют сле-
дующие методы, основанные на оптимизации параметров измерительной сис-
темы; на введении последовательных корректирующих звеньев; на введении
корректирующих обратных связей; на использовании систем с переменной
структурой [4].
В качестве примера рассмотрим оптимизацию параметров измерительной
системы второго порядка из условия минимума длительности переходного
процесса. На рис. 5.6 представлены графики переходных процессов в системе
второго порядка для трех близких значений β.
Минимум длительности переходного процесса будет при таком значении
β
=
β
1
, при котором кривая после первого перехода через установившееся зна-
чение совпадет с верхней границей допустимой динамической ошибки +∆ (кри-
вая 1 входит в зону допуска в точке A, длительность переходного процесса t
1
).
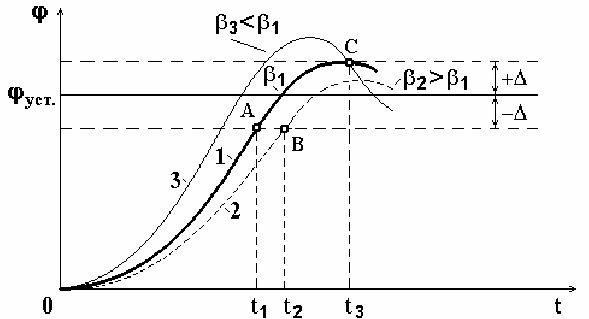
47
Допустим, что β
2
>
β
1
, тогда период колебаний увеличится, и переходный
процесс будет описываться кривой 2, расположенной правее кривой 1 и входя-
щей в зону ±
∆ в точке B, для которой t
2
>
t
1
.
Рис. 5.6. К расчету оптимальной степени успокоения по
критерию минимума длительности переходного процесса
Если же β
3
<
β
1
(кривая 3), то период колебаний уменьшится, но увеличится
величина перехода через установившееся значение, из-за чего максимальное
отклонение кривой 3 выйдет за пределы верхней границы допуска +∆. Дли-
тельность процесса t
3
будет определяться вторым пересечением кривой 3 с
верхней границей зоны допусков в точке C, следовательно, t
3
>
t
1
.
Более подробно вопросы синтеза систем и анализа их динамической точно-
сти рассмотрены в работе [5].
Глава 6. Расчет погрешностей приборов и систем
Определение погрешностей измерительного звена
по его расчетной характеристике
Оценка погрешностей прибора значительно упрощается, если их расчет
разделить на два этапа. На первом этапе определяются погрешности каждого
звена в отдельности по его расчетной характеристике. На втором этапе опреде-
ляются погрешности прибора в целом, с учетом его структурной схемы.
Такая последовательность расчетов не только упрощает вычисления, но и
повышает наглядность полученных результатов, так как выявляется роль каж-
дого звена в формировании общей погрешности прибора.
Кроме того, для выполнения расчета на втором этапе не обязательно иметь
расчетные данные о погрешностях каждого звена. Могут быть использованы
экспериментальные данные или взяты значения погрешностей отдельных
звеньев из технических условий (если используются типовые чувствительные
или преобразующие элементы).
Вернемся к расчетной (5.2) характеристике прибора:
У = f(X, q
1
, q
2
, ..., q
n
),
где q
1
, q
2
, ..., q
n
– параметры схемы и конструкции.
48
Первичные ошибки ∆q
1
, ∆q
2
, ..., ∆q
n
практически малы по сравнению с па-
раметрами q
1
, q
2
, ..., q
n
. Зависимость между приращением выходного сигнала
∆У и первичными ошибками, по аналогии с рассмотренными ранее уравнения-
ми (1.4-1.5), можно представить в виде
∆У = (∂у/∂q
1
)∆q
1
+ (∂у/∂q
2
)∆q
2
, ... + (∂у/∂q
n
)∆q
n
=
= Σ(∂у/∂q
i
)∆q
i
. (6.1)
Таким образом, абсолютная погрешность есть взвешенная сумма первич-
ных погрешностей. Коэффициентами веса являются частные производные по
параметрам, которые вызывают появление погрешностей. Частные производ-
ные вычисляются для расчетных (номинальных) значений q
1
, q
2
, ..., q
n
.
Уравнение (6.1) применимо как к прибору в целом, так и к отдельным его
элементам. Параметры q
1
, q
2
, ..., q
n
могут отличаться от номинальных значений
как по производственно-технологическим причинам (∆q
i
=∆q'
i
– основная по-
грешность), так и из-за отклонения условий эксплуатации (температуры, давле-
ния и др.) от нормальных (∆q
i
=∆q''
i
– дополнительная погрешность).
В качестве примера рассмотрим расчет погрешности маятникового акселе-
рометра (рис. 5.1). Статическую характеристику прибора (5.11) можно предста-
вить следующим образом
U
вых
= 12mlLU
o
b
-1
h
-3
E
-1
ϕ
o
-1
a. (6.2)
На основании уравнения (6.1) получим
∆U
вых
= 12lLU
o
b
-1
h
-3
E
-1
ϕ
o
-1
a∆m + 12mLU
o
b
-1
h
-3
E
-1
ϕ
o
-1
a∆l +
+ 12mlU
o
b
-1
h
-3
E
-1
ϕ
o
-1
a∆L + 12mlLb
-1
h
-3
E
-1
ϕ
o
-1
a∆U
o
–
– 12mlLU
o
b
-2
h
-3
E
-1
ϕ
o
-1
a∆b - 3⋅12mlLU
o
b
-1
h
-4
E
-1
ϕ
o
-1
a∆h –
– 12mlLU
o
b
-1
h
-3
E
-2
ϕ
o
-1
a∆E - 12mlLU
o
b
-1
h
-3
E
-1
ϕ
o
-2
a∆ϕ
o
. (6.3)
Выражение для относительной погрешности получим путем деления урав-
нения (6.3) на уравнение (6.2):
δ
Uвых
= ∆U
вых
/U
вых
=
= ∆m/m + ∆l/l + ∆L/L + ∆U
o
/U
o
– ∆b/b – 3∆h/h – ∆E/E – ∆ϕ
o
/ϕ
o
. (6.4)
Отсюда следует, что относительная погрешность маятникового акселеро-
метра есть взвешенная сумма первичных относительных погрешностей. Коэф-
фициентами веса являются показатели степени параметров.
Выражение (6.1) можно использовать для расчета температурных погреш-
ностей, если считать, что приращения ∆q
i
параметров q
i
произошли в результа-
те изменения температуры окружающей среды.
Полагая параметры q
i
линейно зависящими от температуры
q
i
= q
io
(1+α
i
Θ), (6.5)
получим приращения этих параметров в виде
∆q
i
= q
i
– q
io
= q
io
α
i
Θ, (6.6)
здесь α
i
– температурный коэффициент параметра; q
io
– значение параметра при
нормальной температуре.
49
Подставляя зависимость (6.6) в выражение (6.1), найдем температурную
погрешность прибора:
∆У = Σ(∂у/∂q
i
)q
io
α
i
Θ, (6.7)
откуда условие температурной компенсации будет
Σ(∂у/∂q
i
)q
io
α
i
Θ = 0. (6.8)
Определение погрешностей прибора по структурной схеме
Для расчета погрешности прибора по структурной схеме необходимо знать
погрешности всех его преобразующих звеньев, которые могут быть определены
различными способами: а) расчетным путем по методике, описанной в преды-
дущем параграфе; б) по результатам экспериментальных исследований образ-
цов; в) по справочным данным, если используются стандартные звенья.
Допустим, что прибор (или измерительная система) содержит n звеньев,
каждое из которых осуществляет определенное функциональное преобразова-
ние физических величин. Звенья соединены между собой любым способом (по-
следовательно, параллельно, встречно-параллельно или более сложным обра-
зом). Обозначим выходной и входной сигналы системы в целом через У и Х, а
выходные сигналы звеньев через У
1
, У
2
, ..., У
n
.
В реальной системе сигналы звеньев У
1
, У
2
, ..., У
n
, вследствие наличия у
них погрешностей, получают независимые приращения ∆У
1
, ∆У
2
, ..., ∆У
n
, кото-
рые в совокупности и дают суммарную погрешность системы ∆У.
Относительная погрешность системы в линейном приближении равна ли-
нейной комбинации относительных погрешностей звеньев:
δ = ξ
1
δ
1
+ ξ
2
δ
2
+ ... + ξ
n
δ
n
= Σξ
i
δ
i
, (6.9)
здесь δ = ∆У/У – относительная погрешность системы; δ
i
= ∆У
i
/У
i
– относи-
тельная погрешность i-го звена; ξ
i
– коэффициент влияния i-го звена.
Из уравнения (6.9) следует, что погрешность системы складывается из n со-
ставляющих, каждая из которых порождается соответствующим звеном струк-
турной схемы. Коэффициент влияния ξ
i
представляет собой безразмерный
множитель, на который нужно умножить относительную погрешность i-го зве-
на, чтобы определить порождаемую ею составляющую суммарной относитель-
ной погрешности системы.
Предположим, что все звенья, кроме i-го, абсолютно точны, а погрешность
системы вызвана лишь влиянием i-го звена. Тогда относительная погрешность
системы
∆У/У = ξ
i
∆У
i
/У
i
,
откуда
ξ
i
= (∆У/У)/(∆У
i
/У
i
). (6.10)
Ограничимся случаем, когда все звенья имеют линейные характеристики
У
i
= S
i
X
i
, (6.11)
здесь S
i
– чувствительность i-го звена; X
i
– входной сигнал i-го звена.
50
При установившемся режиме, когда X
i
= const, малое приращение функции
(6.11) можно выразить в виде
∆У
i
= ∆S
i
X
i
. (6.12)
Разделив (6.12) на (6.11), получим
∆У
i
/У
i
= ∆S
i
/S
i
. (6.13)
Аналогично для системы в целом
∆У/У = ∆S/S, (6.14)
здесь S – чувствительность системы в целом.
Подставив (6.13) и (6.14) в (6.10), получим
ξ
i
= (∆S/∆S
i
)⋅(S
i
/S). (6.15)
Так как рассматривается лишь одна составляющая суммарной погрешно-
сти, вызванная влиянием i-го звена, а параметры остальных звеньев принима-
ются постоянными, то отношение малых приращений чувствительности можно
заменить частной производной:
∆S/∆S
i
≈ ∂S/∂S
i
. (6.16)
Подставляя (6.16) в (6.15), получим формулу для определения коэффициен-
та влияния i-го звена:
ξ
i
= (∂S/∂S
i
)⋅(S
i
/S). (6.17)
Если произвести расчет чувствительности прибора по структурной схеме,
то можно представить ее как функцию чувствительности звеньев:
S = F(S
1
, S
2
, ..., S
n
). (6.18)
Частные производные ∂S/∂S
i
(i
=
1, 2, ..., n) могут быть найдены поочеред-
ным дифференцированием функции (6.18) по S
1
, S
2
, ..., S
n
.
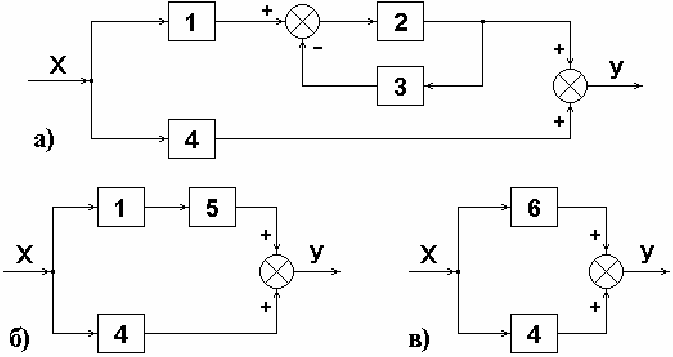
Рассмотрим расчет коэффициентов влияния погрешностей звеньев на при-
мере, представленном в работе [3]. Определим безразмерные коэффициенты
влияния погрешностей звеньев для структурной схемы, приведенной на
рис. 6.1, а, если заданы чувствительности звеньев: S
1
=
20; S
2
=
9; S
3
=
1; S
4
=
2.
Заменим встречно-параллельные звенья 2 и 3 с отрицательной обратной
связью эквивалентным звеном 5 (рис. 6.1, б), чувствительность которого со-
гласно (5.18) равна S
5
= S
2
/(1 + S
2
S
3
).
Рис. 6.1. К примеру расчета коэффициентов влияния
