Шпоры - Моделирование экономики

Подождите немного. Документ загружается.

Моделирование экономики.

1. ВОПРОС 1. Особенности, принципы

математического моделирования

Моделирования являются процессом построения,

изучение и применение моделей. Оно объединено с

такими категориями, как абстракция, аналогия, гипотеза и

т.п.. Процесс моделирования обязательно включает

конструирование научных гипотез.

Главная особенность моделирования состоит в потому,

что это метод опосредствованного познания с помощью

об'єктів-заміщувачів. Модель возникает как своеобразный

инструмент познания, которое его исследователь

(системный аналитик) ставит между собою и объектом и

с помощью которого изучает объект, который его

интересует. Именно эта особенность моделирования

определяет специфические формы использования

абстракций, аналогий, гипотез, других категорий и

методов познания.

Необходимость использования моделирование

определяется тем, что много объектов (или аспектов,

которые касаются этих объектов) непосредственно

исследовать или вообще невозможно, или это требует

много времени и средств.

Пусть необходимо создать некоторый объект А. Мы

конструируем (материально или в воображении) или

находим в реальном мире другой объект B - модель

объекта A. Можно видокремити такие четыре основных

этапа построения модели.

Первый этап предусматривает наличие некоторых

знаний об объекте-оригинале. Познавательные

возможности модели предопределяются тем, что модель

отображает, с точки зрения системного аналитика,

существенные черты объекта-оригинала. Вопрос о

необходимости и достаточности подібності оригинала и

модели требует анализа. Очевидно, модель теряет смысл

как в случае тождественности с оригиналом (тогда она не

перестает быть оригиналом), так и в случае чрезмерного

во всех существенных отношениях упрощения. Изучение

одних свойств моделированного объекта происходит по

счет отказа от отображения других сторон. Через это

любая модель заміщує оригинал только в строго

ограниченном смысле. Из этого вытекает, что для одного

объекта может быть построен несколько

"специализированных" моделей, которые концентрируют

внимание на определенных сторонах исследуемого

объекта ли характеризуют объект с разным уровнем

детализации.

На втором этапе модель возникает как самостоятельный

объект дослі-дження. Одной из форм такого исследования

есть проведение "модельных" экспериментов, за которые

сознательно изменяют условия функционирования

модели и систематизируют данные про ее "поведение".

Окончательным результатом этого этапа есть множество

знаний о модели В.

На третьем этапе осуществляется перенесение знаний из

модели на оригинал - формирование множества знаний S

об объекте. Этот процесс перенесения знаний проводится

по определенным правилам. Знание о модели должны

быть скорректированными с учетом тех свойств объекта-

оригинала, которые не нашло отображения ли были

деформированными во время построения модели. Мы

можем с достаточным основанием переносить какой-

нибудь результат из модели на оригинал, если этот

результат обязательно связан с признаками сходства

оригинала и модели. Если же определенный результат

модельного исследования связанный с отличием Моделі

от оригинала, то его переносить неправомерно.

Четвертый этап - практическая проверка полученных за

допомогою моделей знаний и использования их для

построения обобщающей теории объекта или управления

ним.

Для понимания сущности моделирование важно иметь в

виду, что моделирование - не единый источник получения

новых знаний об объекте. Процесс моделирования

"погружен" в более общий процесс познания. Это

учитывается не только на этапе построения Моделі, а и на

завершающей стадии, если происходит объединение и

обобщение результатов исследования, которые получают

на основании разнообразных средств познания.

Моделирование - циклический процесс: за первым

четырехэтапным циклом может настать второй, третий и

т.п.. При этом знание об исследуемом объекте

расширяются и уточняются, а исходная модель

постепенно усовершенствуется. Недостатки, которые

обнаруживаются после первого цикла моделирования,

которые обусловленные, например, недостаточным

изучением объекта и ошибками в построении модели,

можно исправить в следующих циклах.

Системные аналитики обязаны руководствоваться также

принципами относительно концепции "математическая

модель" некоторого объекта.

Принцип 1. Диалектический пар модель-объект всегда

полярна, имеет два полюса - "модель" и "объект".

Принцип 2. С двух взаимосвязанных полюсов

диалектического пара модель-объект один есть

первичным, другой - производный от него.

Принцип 3. Наличия полюса "объект" недостаточно для

наличия полюса "модель", наличие полюса "модель"

предопределяет необходимость наличия полюса "объект".

Принцип 4. Как "модель" для данного "объекта", так и

"объект" для данной "модели" семантически и

інтерпретаційно многозначные: "модель" віддзеркалює

свойства не одного, а многих "объектов", "объект"

описывается не одной, а многими "моделями".

Принцип 5. "Модель" должна быть адекватной

"объектовые" и отображать с определенной точностью

основные его черты и свойства в зависимости от целей

исследования, имеющейся информации, приемлемой

системы гипотез.

2. ВОПРОС 2. Особенности математического

моделирования экономики.

Под экономико-математической моделью понимают

концентрированное выражение найсуттєвіших

экономических взаимосвязей исследуемых объектов

(процессов) в виде математических функций, неравенств

и уравнений.

Под моделированием понимают процесс построения,

изучение и использование моделей. Он тесно объединен с

такими категориями, как абстракция, аналогия, гипотеза и

т.п..

Процесс моделирования включает три системотвірних

элемента:

" субъект исследования (системный аналитик);

" объект исследования;

" модель, которая опосредствует отношения между

объектом, который изучается, и субъектом, который

познает (системным аналитиком).

Подчеркнем, что математическая модель - это объект,

который создается системным аналитиком для получения

новых знаний об объекте-оригинале и отбивает лишь

существенные (с точки зрения системного аналитика)

свойства объекта-оригинала. Анализируя сущность

указанного высшее, можно сделать, вчастности, такие

выводы:

а) любая модель есть субъективной, она несет в себе

характерные особенности индивидуальности системного

аналитика;

б) любая модель есть гомоморфною, то есть в ней

отбиваются (отражаются) не все, а лишь существенные

свойства объекта-оригинала исходя из целей

исследования, взятой системы гипотез и т.п.;

в) возможное существование множества моделей одного

и одного и того же объекта-оригинала, которые

отличаются целями исследования, степенью адекватности

и т.п..

Модель считается адекватной объекта-оригинала, если

она с достаточной степенью приближения, на равные

понимания системным аналитиком моделированного

процесса отображает закономерности процесса

функционирование реальной экономической системы в

зовнішньому относительно объекта исследования среде.

3. ВОПРОС 3. Этапы экономико-математического

моделирования

1. Постановка экономической проблемы и ее

качественный анализ.

Главное здесь - четко сформулировать сущность

проблемы (целые исследования), предположение,

которые принимаются, и те вопросы, на которые

необходимо получить ответы. Этот этап включает

выделение важнейших черт и свойств объекта, который

моделируется, и абстрагирование от второстепенных;

изучение структуры объекта и главных зависимостей,

которые объединяют его элементы; формулирование

гипотез (хотя бы предшествующих), что объясняют

поведение и развитие объекта.

2. Построение математических моделей.

Это - этап формализации экономической проблемы,

выражение ее в виде конкретных математических

зависимостей и отношений (функций, уравнений,

неравенств и т.п.). Сначала определяется основная

конструкция (тип) математической модели, а потом

уточняются детали этой конструкции (конкретный

перечень сменных и параметров, форма связей). Таким

образом, построение модели имеет несколько стадий.

3. Математический анализ модели.

Целью этого этапа есть выяснение общих свойств модели.

Здесь часто применяют математические приемы

исследования. Важнейший момент - доведение

существования решений в сформированной модели

(теорема существование). Если повезет доказать, что

математическая задача не имеет решения, то

необходимость в следующей работе за первоначальным

вариантом модели отпадает; следует скорректировать ли

постановку экономической задачи, модифицировать ли

ее математическую формализацию.

4. Подготовка исходной информации.

В процессе подготовки информации широко

используются методы теории вероятностей,

теоретической и математической статистики. В

статистическом экономико-математическом

моделировании результирующая информация,

используемая в одних моделях, есть исходной для

функционирования других моделей.

5. Числовые развязки.

Этот этап включает разработку алгоритмов для числового

решения задачи, составление программ на ЭВМ и

непосредственное проведение расчетов. Трудность этого

этапа обусловлена прежде всего большой размерностью

экономических задач, необходимостью обработки

значительных массивов информации.

6. Анализ числовых результатов и их использование.

На этом, завершающем, этапе цикла возникает вопрос о

правильности и полноте результатов моделирования, об

уровне практического применения последних.

Математические методы проверки могут проявлять

некорректность подхода к построению модели и тот

самим суживать класс потенциально правильных

моделей. Неформальный анализ теоретических выводов и

числовых результатов, которые получают с помощью

модели, сопоставление их с знаниями, которыми владеем,

и фактами действительности также разрешат находить

недостатки постановки экономической задачи,

сконструированной математической модели, ее

информационного и математического обеспечения.

4. ВОПРОС 4. Основные характеристики экономико-

математических моделей.

Каждая экономико-математическая модель реального

явления характеризуется:

а) объектом моделирования;

б) системным описанием объекта;

в) целями относительно построения модели;

г) принципами моделирования;

д) аппаратом моделирования;

есть) способами идентификации и интерпретации

результатов.

Объектом моделирования может быть или реальная

хозяйственная система, или одних или несколько

процессов, которые развиваются в такой системе. Для

построения модели надо не просто указать наименования

объекта, а и дать его описание в виде системы, то есть

обнаружить существенные грани его взаимодействия с

внешней средой, его структуру. Модели, которые

отображают (заменяют) один и тот же объект из разных

взглядов, следует считать разными.

Аппарат моделирования определяется типом

математических конструкций, которые используются для

построения модели. Наиболее распространенными

являются модели, построенные с помощью аппарата

линейной алгебры, регрессионного анализа, линейных

дифференционных уравнений. Иногда говорят о

специфическом аппарате - "аппарат производственной

функции". Выбор того ли другого аппарата экономико-

математического моделирования в значительной мере

грунтуется на гипотезах, которые положенные в основу

построения модели.

5. ВОПРОС5. Общее понятие производственной

функции.

Производственная функция характеризует зависимость

между количеством применяемых ресурсов и

результатами производства.

Нашей задачей есть выделить из множества моделей

производственную функцию (ПФ) как особый вид

экономико-статистических моделей. Рассмотрите с этой

целью содержание любой из признаков: А-Е (п. 5.2) :

А. Объект моделирования. Непосредственным объектом

моделирования относительно ПФ являются процессы

производства продукции в реально функционуючих на

протяжении определенного отрезку времени

хозяйственных системах на предприятии (фирме), в

области, регионе ли в народном хозяйстве вообще.

Соответственно, относительно уровня моделированной

системи производственные функции делятся на

макроэкономические, региональные, отраслевые, а также

производственные функции предприятия.

Б. Системное описание объекта. В теории

производственных функций производственный процесс

анализируется с точки зрения преобразования ресурсов в

продукт (продукцию). Входами являются потоки

ресурсов разнообразного вида, полностью или частично

используемые в производстве, выходом - готовая к

реализации продукция. Функционирующие в системе

ресурсы (факторы), технология и условия организации

производства определяют потенциальные возможности и

состояние процесса (системы).

В. Целые моделирования. ПФ строится для решения

определенных экономических задач, которые касаются

анализа, прогнозирование и планирование (в узком

понимании слова). Используются ПФ как самостоятельно,

так и в составе более общих экономико-математических

моделей. Цель построения ПФ можно охарактеризувати

как анализ факторов относительно существенного

влияния их на объемы выпуска продукции.

Г. Принципы моделирования. В основе наиболее

распространенного понятия ВФ лежат принципы,

которые выражают роль аксиоматических положений

теории производственных функций:

1) объем выпуска продукции, выработанной данной

производственной системой за определенный период,

определяется объемами средств и предметов работы и

живой работы, которые принимают участие в процессе

производства в течение этого периода;

2) связь между объемами выпуска и объемами средств

работы, предметов работы и живой работы есть для

данной производственной системы закономерным и

относительно стойким;

3) в ряде случаев дополнительно берется гипотеза,

которая в определенных границах любое независимое

изменение аргументов ВФ допускает реальную

интерпретацию.

Д. Аппарат моделирования. Основным "материалом"

для построения производственной функции являются

зависимости y = f (x1, ..., xn), где y - показатель выпуска

(объем), x1, ..., xn - объемы производственных ресурсов

(факторов) (количество факторов ПФ, как правило, не

превышает 10). Функция f (·) считается определенной в

довольно широкой области n-мерного евклі-дового

просторную (R

) и такой, что вычисляется в области

своего определения. Последнее означает, что системный

аналитик должен мати в своем распоряжении алгоритм,

который разрешал бы вычисливатты значения f (·) в

любой точке, где она определенная. Как правило, ПФ y =

f (x1, ..., xn) строится путем подбора наиболее адекватных

функций из определенного параметрического класса

FN=N{y = f



, ..., x

, a

, ..., a

)} = f



(x, a), где a=N(a

, ..., a

) -

вектор параметров.

Итак, непосредственным аппаратом моделирования в

границах данной концепции ПФ являются

параметрические классы функций, которые зависят от

сменных. Как правило, зависимость функции f



(·) от

сменных и параметров задается в явном виде (или

режиме) ли в виде функциональных дифференциальных

или интегральных уравнений.

Э. Идентификация и интерпретация модели.

Изменяемые y,x

,N...,Nx

отождествляются с показателями

объемов выпуска и основными, которые принимают

участие в производстве, факторами (ресурсами).

Припуска-ється возможность спецификации параметров

,N…,Na

ПФ на основании статистических (ли

экспертных) данных относительно ресурсов и выпуска

продукции за предшествующие периоды, а также

плановых и опосредствованных данных. Метод оценки

параметров не определяется однозначно, он зависит от

целей построения ПФ, особенностей моделированного

процесса и исходных данных. Интерпретация параметров,

в свою очередь, зависит от метода их оценивания. Часто

для интерпретации виокремлених параметров

привлекаются их выражения через значение показателей,

а также значение частичных производных

....,,1, ni





6. ВОПРОС 6. Экономическое содержание

производственной функции.

Производственная функция - Экономико-

математическая зависимость в форме связи между

количеством производимой продукции и

использованными при ее создании факторами

производства, в качестве которых в этой функции

рассматриваются труд и капитал.

Производственные функции в широком смысле

охватывают моделирование зависимостей, существующих

между такими показателями производственной

деятельности, как объем выпускаемой продукции,

капитальные затраты, фондоотдача, производительность

труда и др.

Цель построения производственных функций –

количественно оценить, измерить характер и степень

влияния различных факторов на результат процесса

производства. Одним из наиболее важных направлений

использования аппарата производственных функций

является анализ эффективности ресурсов производства.

С помощью производственных функций можно

исследовать эффективность трудовых затрат,

производственных фондов, природных и других ресурсов

не изолированно, а в их взаимодействии, выявить

границы взаимозаменяемости ресурсов и наиболее

рациональные их пропорции с точки зрения конечного

результата производства. Широкие возможности

открывают производственные функции для анализа

научно-технического прогресса и его влияния на

Моделирование окончательное

общественное производство, на общие темпы

экономического развития.

Существенную роль играют производственные функции

как инструмент прогнозирования конечных результатов

производственной деятельности. На основе анализа

количественного роста и повышения эффективности

ресурсов общественного производства, типа и темпа

научно-технического прогресса производственные

функции дают возможность рассчитать прогнозируемые

величины национального дохода и других

результативных экономических показателей как на

ближайшую, так и достаточно отдаленную перспективу.

7. ВОПРОС 7. Общая характеристика и этапы

построения производственных функций.

Понятие ПФ определенного объекта как функции,

которая вместе с областью определения наилучшим

образом аппроксимирует агреговану экономическую

технологию  , определяет строгую последовательность

действий для построения ПФ.

Поскольку ПФ строится в результате использования

числительного метода и оптимизаци V, этапом в этом

построении есть использование так называемых пробных

функций и областей их определения, то есть выбор

бинарного отношения 



на множестве числительных

функций. Выбор этого отношения сыграет

определяющую роль в построении ПФ, поскольку в него

входит и определение вида функции, и формирование

принципов оценивание параметров. Для этого нужно

собрать, обработать и использовать необходимую

информацию относительно производственного процесса

и влияния на него внешних условий, сформулировать

цели и задача, для решения которых строится ПФ,

проанализировать основы существование и свойства

экономико-технологической функции ; как правило,

предварительно фиксируется система показателей оценки

ресурсов и выпуска (,N).

Выделяют такие этапы построения ПФ:

Этап 1. Формулирование целей построения ПФ.

Этап 2. Системный анализ объекта, который

моделируется.

Этап 3. Экономический качественный анализ объекта.

Этап 4. Определение системы показателей

производственной функции (,N).

Этап 5. Формирование информационной базы для анализа

техноло-гії и для построения ПФ.

Этап 6. Анализ существования и свойства экономической

технологии.

Этап 7. Определение принципов сравнения функций

относительно их приближения к технологии 

(формирование отношение) N=N



Этап 8. Определение вычислительного алгоритма V для

оптимизации отношение 



Этап 9. Подготовка (выбор) программного обеспечения

относительно реализации алгоритма на компьютере.

Этап 10. Вычисление ПФ и ее использование.

8. ВОПРОС 8. Виды производственных функций

(производственные функции Леонтьева, Кобба-

Дугласа, линейная).

Функция с фиксированными пропорциями факторов

(функция Леонтьєва).















,min

, (5.1)

где а

, а

— параметри.

Известно несколько альтернативных систем (гипотез),

которые виокремлюють функции этого вида:

а) предельная производительность первого фактора есть

двухуровневой кусков-постоянной невозрастающей

функцией от соотношения с нулевым нижним уровнем.

Предельная производительность второго фактора -

ненисходящая кусков-постоянная функция от с нулевым

нижним уровнем;

б) функция есть розв'язком такой задачи математического

программирования:

max,

xya





де у — сменная, которую оптимізують;

в) функция есть однородной, а эластичность замены

факторов равняется нулю;

г) функция может быть получена из функции с постоянной

эластичностью вида

путем предельного перехода:

a

Функция Леонтьєва предназначена в основном для

моделирования строго детермінованих технологий,

которые не допускают отклонения от технологических

норм и нормативов относительно использования ресурсов

на единицу продукции. Как правило, она используется

для формализованного описания мелкомасштабных или

целиком автоматизированных объектов.

Функция Кобба-Дугласа

210

xxay 

Здесь также используется несколько систем гипотез,

которые виокремлюють класс функций Кобба-Дугласа

среди дважды дифференцированных функций от двух

сменных:

а) эластичности выпуска за факторами есть постоянными:

; a









Розв'язок этой системы дифференционных уравнений в

частинних производных первого порядка належит к классу

функций Кобба-Дугласа;

б) эластичность функции за одним из факторов есть постоянной,

и функция есть однородной;

в) функция есть однородной, а эластичности уменьшения

факторов за Алленом и Михайловським равняются единицы;

г) предельная производительность каждого фактора есть

пропорциональной его средней производительности;

д) функция есть однородной как функция от х

, х

и как

функция от х

за любого фиксированного х

;

е) функция может быть получена из функции с

постоянной эластичностью путем осуществления замены

вида

333

22110

)(

aaa

xaxaay 

и предельного перехода а

NN0. Функция Кобба-Дугласа

наиболее частое используется для формализованного

описания середньомасштабних хозяйственных объектов и

экономики страны.

Линейная функція

2211

xaxay 

Предпосылки и гипотезы:

а) предельные производительност факторов есть

постоянными:

; a









а в нуле функция приобретает нулевого значения;

б) предельная производительность одного из факторов

есть постоянной, и функция однородная первой степени:













;

в) функция однородная, и эластичность замены факторов,

за Алленом, есть бесконечной;

г) эластичность выпуска за факторами обратно

пропорциональная их средний производительности.

Линейная функция применяется для моделирования

крупномасштабных систем (большая область, народное

хозяйство в целом), в которых выпуск продукции есть

результатом одновременного функционирования

большого количества разнообразных технологий. Особую

роль сыграет гипотеза постоянности предельных

производственных факторов ли их неограниченного

замещения.

9. ВОПРОС 9. Экономико-математическая модель

межотраслевого баланса (модель Леонтьева «затраты-

выпуск»).

Основу информационного обеспечения модели

межотраслевого баланса составляет технологическая

матрица, которая содержит коэффициенты прямых

материальных затрат на производство единицы

продукции. Эта матрица есть базой экономико-

математической модели межотраслевого баланса.

Допускает гипотеза, в соответствии с которой для

производства единицы продукции в j-й области

необходимое определенное количество затрат

промежуточной продукции і-ї области, которые

составляет a

, и эта величина не зависит от объемов

производства в j-й области и есть довольно стабильной

величиной в времени. Величины a

называют

коэффициентами прямых материальных затрат и

вычисляют таким образом:

....,,1,,const, njia



(11.4)

Коэффициенты прямых материальных затрат показывают,

какое количество продукции і-ї галузі необходимо

израсходовать, если учитывать лишь прямые затраты, для

производства единицы продукции j-ї области. С учетом

формулы (11.4) систему уравнений баланса (11.2) можно

записать в виде





....,,1, niY



(11.5)

Если ввести к рассмотрению матрицу коэффициентов

прямых материальных затрат А = (а

), вектор-столбик

валовой продукции X и вектор-столбик конечной

продукции Y:































это система уравнений (11.5) в матричной форме будет

иметь вид

X = AX + Y . (11.6)

 Систему уравнений (11.5), в ли матричной форме

(11.6), называют экономико-математической моделью

межотраслевого баланса (моделью Леонтьєва, моделью

"затраты - выпуск"). С помощью этой модели можно

выполнить три варианта вычислений:



" задавая в модели объемы валовой продукции

каждой области (Х

), можно определить объемы конечной

продукции каждой области (Y

Y = (E – A)X, (11.7)

где Е — единичная матрица n-го порядка;

 " задавая объемы конечной продукции всех

областей (Y

), можно определить объемы валовой

продукции каждой области (Х

X = (E – A)

–1

Y; (11.8)

" для ряда областей задавая объемы валовой продукции,

а для остатка - объемы конечной продукции, можно

отыскать величины конечной и валовой продукции всех

областей.

В формулах (11.7) и (11.8) Е обозначает единичную

матрицу

n-го порядка, а (Е – А)

–1

— матрицу, обратную к матрице

(Е – А).

10. ВОПРОС 10. Функция полезности.

Фу́нкция поле́зности — экономическая модель для

определения предпочтений экономических субъектов.

Основоположным условием концепта функции

полезности является рациональное поведение

потребителя, выражающееся в выборе из

многочисленных альтернатив именно тех, которые

выводят его на более высокий уровень полезности. В

микроэкономике концепт функции полезности служит

для объяснения поведения потребителей и

производителей, в то время как в макроэкономике им

пользуются для изображения предпочтений

государственных интересов. Первая производная

функции полезности по количеству определённого блага

называется предельной полезностью этого блага.

Предельная полезность выражает, сколько

дополнительной полезности приносит дополнительная

единица блага i. Предельная полезность, равная 0,

означает достижение насыщенности.

11. –ВОПРОС 11. Преимущества потребителя и его

функция полезности.

12. ВОПРОС 12. Модель поведения потребителя.

Поведение потребителя - это процесс формирования

рыночного спроса покупателей, осуществляющих

выбор благ с учетом существующих цен.

Модель поведения потребителя представляет собой

связанные между собой общие принципы поведения

потребителя на рынке, включающие в себя, прежде

всего, максимизацию совокупной полезности, закон

убывающей предельной полезности и бюджетное

ограничение.

Некоторые принципы поведения потребителя на рынке,

то есть модель его поведения.

- выбирая блага для потребления, покупатель

руководствуется своими предпочтениями;

- поведение потребителя является рациональным, в

частности он выдвигает определенные цели и

руководствуется личным интересом, то есть действует в

рамках разумного эгоизма;

- потребитель стремится максимизировать совокупную

полезность, другими словами, стремится выбрать такой

набор благ, который приносит ему наибольшую общую

величину полезности;

- на выбор потребителя и его субъективные оценки

полезности покупаемых благ влияет закон убывающей

предельной полезности;

- при выборе благ возможности потребителя

ограничены ценами благ и его доходом; данное

ограничение называется бюджетным ограничением.

13. ВОПРОС 13. Уравнение Слуцкого (модель

поведения потребителя).

Уравнение Слуцкого — уравнение, смысл которого

состоит в том, что изменение спроса на некоторый товар

при повышении или снижении его цены складывается из

влияния непосредственного изменения спроса и

косвенного влияния в результате переключения спроса на

другие товары.

Рассмотрим равенство

(3.7.5)

Равенство (3.7.5) называется уравнением Слуцкого. Это же

уравнение называют основным уравнением теории

ценности.

В координатной форме уравнение Слуцкого выглядит так:

(3.7.6)

Левую часть уравнения принято называть общим

эффектом (от влияния цены на спрос), первое слагаемое

в правой части - влиянием замены (т.е.

компенсированного изменения цены на спрос), второе

слагаемое - влиянием дохода (влияние изменения дохода

на спрос). Перепишем уравнение следующим образом:

(3.7.7)

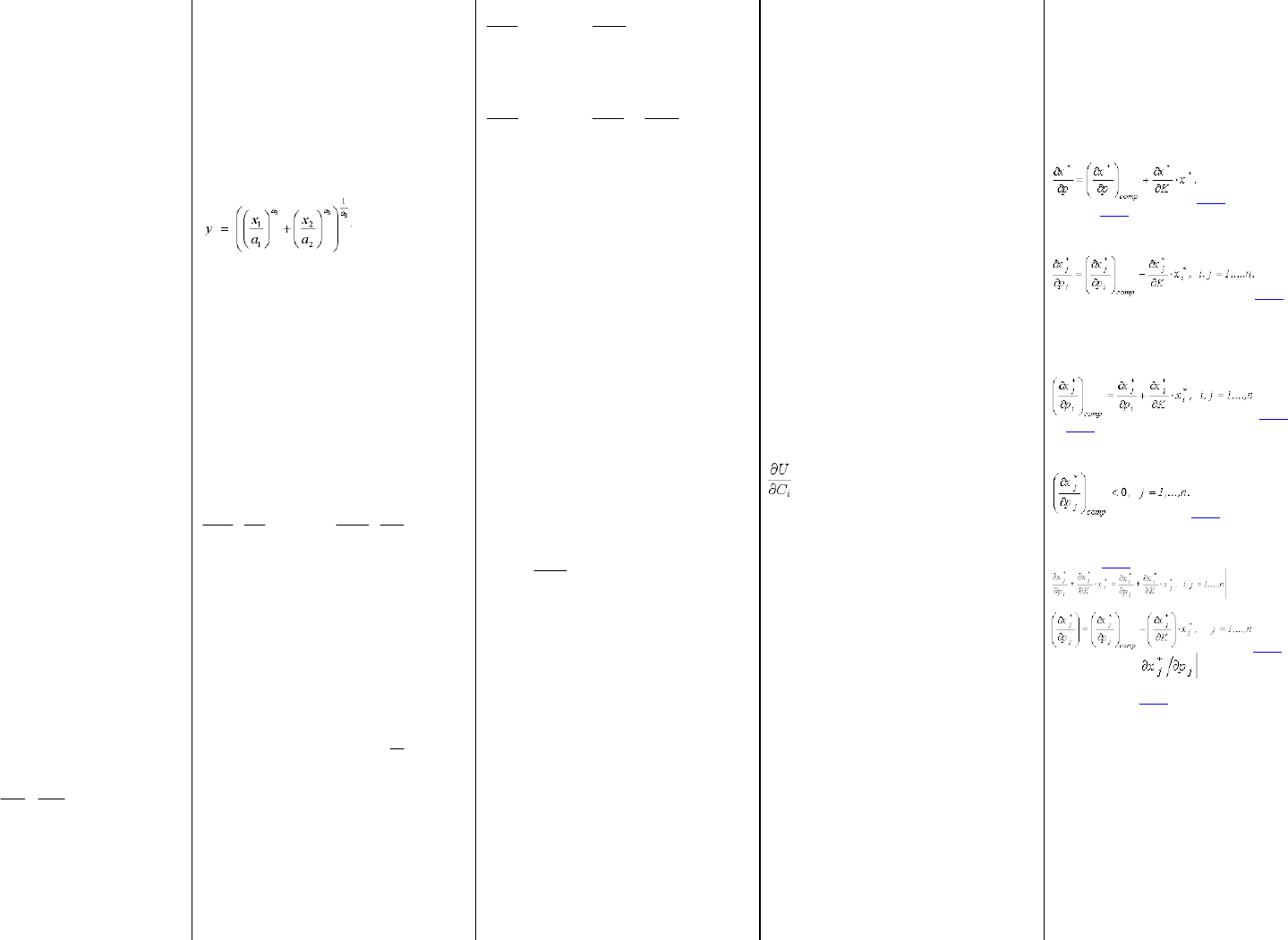
Из (3.7.4) следует, что матрица влияния замены

симметрична и отрицательно определена (установите это

самостоятельно). Из отрицательной определенности

следует

(3.7.8)

Отсюда вывод - компенсированное возрастание цены

товара приводит к уменьшению спроса на этот товар.

Их симметричности матрицы влияния замены и

уравнения (3.7.7) получаем:

Поэтому уравнение Слуцкого, в частности, означает, что:

(3.7.9)

Здесь производная называется влиянием на

спрос (на j-й товар) изменения частной цены (цены j-го

товара). Равенство (3.7.9) используют для характеристики

типов товаров.

14. ВОПРОС 14. Модель фирмы (модель поведения

производителей)

Пусть производственная фирма выпускает один продукт

(или много продуктов, но с постоянной структурой).

Годовой выпуск в натурально-вещевой форме X - это

количество единиц продукта одного вида (ли количество

багатономенклатурних агрегатов).

Использованные ресурсы: L - живая труд (в виде средней

численности занятых за год или отработанных за год

человеко-часов); K - средства труда (основные

производственные фонды); M - предметы труда

(израсходованное за год топливо, энергия, сырье,

материалы, комплектовочные изделия и т.п.).

Каждый из агрегованих видов ресурсов (работа, фонды,

материалы) имеет определенное количество

разновидностей.

Моделирование окончательное

Обозначим вектор-столбик возможных объемов затрат

разных видов ресурсов через x = (x

, …, x

). Тогда

технология фирмы будет определяться ее

производственной функцией, которая выражает связь

между затратами ресурсов и выпуском:

X = F(x). (8.1)

Допускает гипотеза, которая F(x) дважды неперервно

дифференцированная и неоклассическая, и вдобавок

матрица ее вторых производных есть від'ємно

определенной.

Если w = (w

, …, w

) — вектор-строка цен ресурсов, а

р — цена продукции, то каждому вектору затрат х

отвечает прибыль:

П(х) = pF(x) – wx. (8.2)

У (8.2) R = pX = pF(x) — стоимость годового выпуска

фирмы или ее годовой доход,C = wx — затраты

производства или стоимость затрат ресурсов за год.

Если не вводить других ограничений, кроме

неотъемлемых затрат ресурсов, то задача на максимум

прибыли наберет вида:

.])([max

wxxpF





(8.3)

Это задача нелинейного программирования с n условиями

неотъемлемости x 0, необходимыми условиями ее

решения есть условия Куна-Таккера:

,0









.0,0 























xxw

(8.4)

Если в оптимальном розв'язку используются все виды

ресурсов, то есть x* > 0, то условия (8.4) будут иметь вид:

)(

p 



(8.5)

или

,...,,1,

)(

njw





то есть в оптимальной точке стоимость предельного

продукта данного ресурса должна равняться его цене.

Такой самый (по форме) розв'язок имеет задача на

максимум выпуска за заданного объема затрат

.0,),(max  xCwxxF

(8.6)

Это задача нелинейного программирования с одним

линейным ограничениям и условием неотъемлемости

сменных.

Построим функцию Лагранжа:

L(x, ) = F(x) +  (C – wx),

теперь максимизируем ее при условии неотъемлемости

сменных.

Для этого необходимо, чтобы выполнялись условия Куна-

Теккера:

.0,0,0 





















xxw

(8.7)

Как видим, условия (8.7) целиком совпадают с (8.4), если

положить



15. ВОПРОС 15.Модель поведения фирмы на

конкурентных рынках (два конкурента).

За совершенной конкуренции, если участников рынка

много, цены на рынке не зависят от действий отдельных

производителей и потребителей. Если же, наоборот,

участников рынка немного, цены на рынке зависят от

стратегий, что их придерживаются эти участники.

Рассмотрите пример с двумя конкурентами, которые

вырабатывают одну и одну и ту же продукцию, каждый

согласно с своей производственной функцией:

.2,1),(  ixFX

В этом случае цена продукции зависит от обоих выпусков

(обоих участников):

,),(

XXpp

причем она снижается с возрастанием выпуска:

.0,0









Цены на ресурсы зависят от объемов их купли:

....,,1,),(

njxxww

jjjj



(8.24)

Цены возрастают за возрастание спроса:

.0,0









Каждая фирма стремится максимизировать свою

прибыль. Например, первая фирма должна действовать

таким чином:

,]),(),([max

121

...,,,







jjjj

xxX

xxxwXXXp

(8.25)

при условии

)....,,(

111 n

xxFX 

Функция Лагранжа имеет вид:







njjjj

XxxFxxxwXXXpxXL

121

),)...,,((),(),(),,(













































.0)...,,(

,...,,1,0),(

,0),(

)1(

)2(

121

)1(

121

XxxF

xxxw

XXXp

jjjj

Исключив  с 1-го уравнение, получим (n + 1) уравнение

для определения стратегии

...,,,

xxX

первой фирмы:

.)...,,(,...,,1

,),(

111

)1(

121

xxFXnj

XXXp

























































(8.26)

Розв'язок этих уравнений зависит от

....,,1,i





Последние есть ожидаемой реакцией второй фирмы на

стратегию

...,,,

xxX

первой.

Делая разные предположения и предполагая гипотезы

относительно этой реакции, получим разные розв'язки

задачи конкуренци.

Проанализируйте разные варианты розв'язку задачи в

упрощенной постановке, если не рассматривается

конкуренция на рынке ресурсов.

Затраты обоих фирм есть одинаковыми линейными

функциями выпуска (с - предельные затраты, d -

постоянные затраты):

,2,1,)(  idcXXC

iii

цена продажи - линейная функция от общего выпуска (Х)

обоих фирм:

р(X) = a – bX, X = X

+ X

(b - спадание цены при условии возрастания на единицу

общего выпуска).

Тогда выражения для прибылей конкурирующих фирм

наберут вида:

,2,1,)]([

)]([),(

210

2121





idXXXbX

dcXXXXbaXX

iii

(8.27)

Где X

= (a – c)

b — величина общего выпуска, за

которой прибыль каждой фирмы есть отрицательным и

равняется - d.

Имеем

,0)1()(

)]([

1210

11210























XXXXb

bXbXXXXb

(8.28)

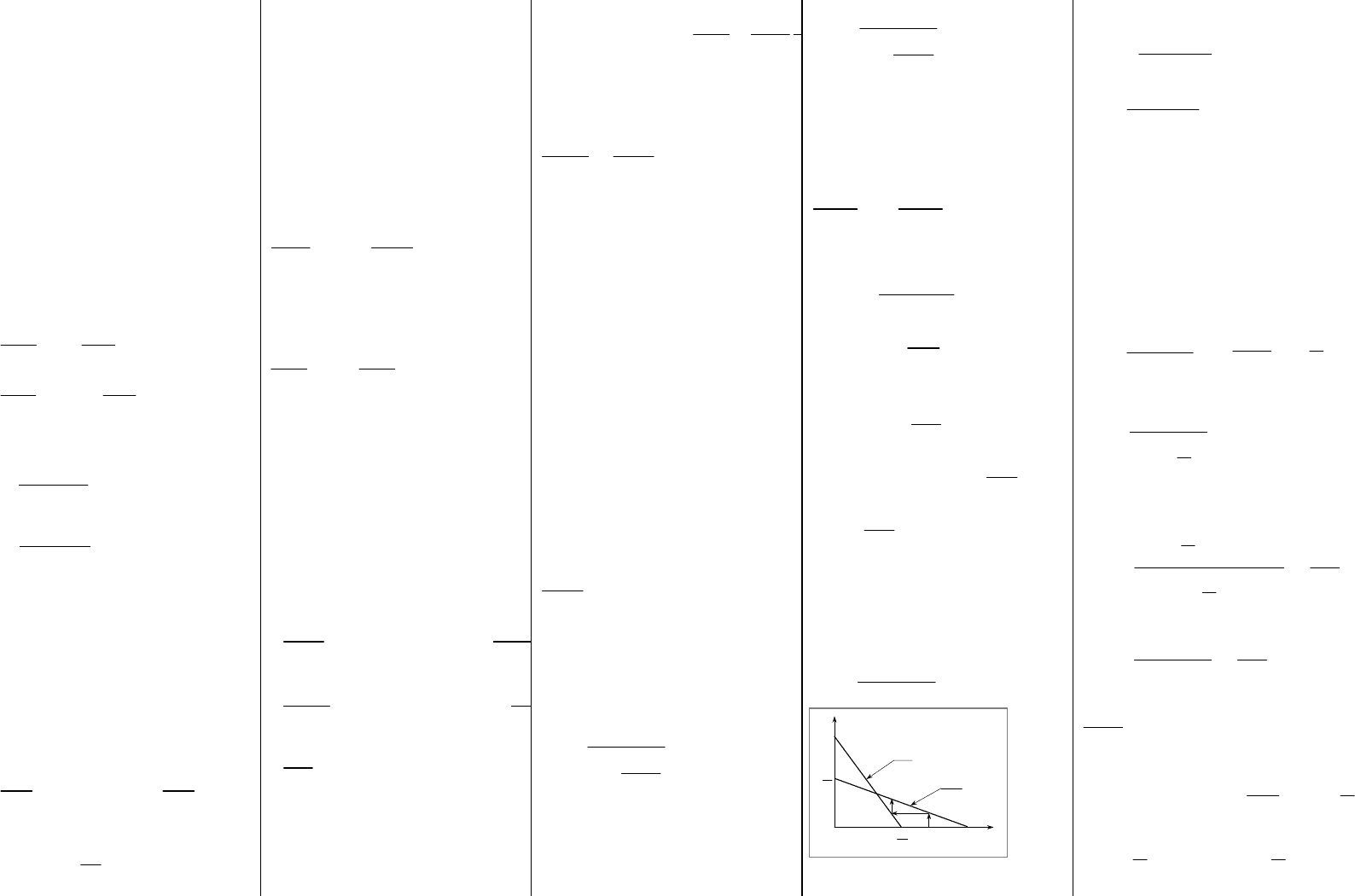
отсюда выпуск, который максимизирует прибыль,

равняется:







Аналогічно







16. ВОПРОС 16. Равновесие по Курно (модель

поведения фирмы на конкурентных рынках).

Рассмотрите случай, если каждая фирма предполагает

гипотезу относительно неизменной стратегии

конкурирующей фирмы (X

— не зависит от X

, и

наоборот), тогда:

0,0



і з (8.29) та (8.30)

видно, що:

XX 

тому





отже,

XX 

Обозначим элементы полученного розв'язку индексом K

(Курно), тогда:

0021

bXabXapXXXX

KKKKKKK



Точка равновесия за Курно



может быть представлена как

результат такого, что сходится, алгоритма Курно: первая

фирма избирает сначала любой випуск

XX 

;

друга действует так, будто первая все время избирала бы

то есть

Точка равновесия за Курно





Перша

Друга

Рис. 8.2. Итерационная процедура нахождения точки

равновесия за Курно

Дале обе фирмы действуют аналогично (l - номер

итерации):











Сходимость данной процедуры можно проследить на рис.

8.2.

На этом рисунке изображенные прямые, которые

означают реакции фирм, любая из которых есть

геометрическим местом точек оптимального выпуска

одной фирмы за заданного фиксированного выпуска

второй. Траектория движения к точке равновесия

показанная стрелками. Как можно заметить, имеет место

монотонная сходимость к точке равновесия

17. ВОПРОС 17. Равновесие и неравновесие по

Стакельбергу (модель поведения фирмы на

конкурентных рынках).

1. Вообразите, что первая фирма предполагает гипотезу,

за которой вторая фирма будет действовать в

соответствии с Курно, то есть:





, тоді





тому випуск первой фирмы, которая максимизирует ее

прибыль (см. (8.29)), будет равняться:





Точку равновесия за Стакельбергом получим, решая

уравнения:

Первая фирма:

)(

100

XXX







Вторая фирма:

010

XXX







За таких стратегий первая фирма получает прибыль:



а вторая лишь

 

164

),(

212

dXX

bXX

















В точке равновесия за Стакельбергом:

bXapXX



Моделирование окончательное

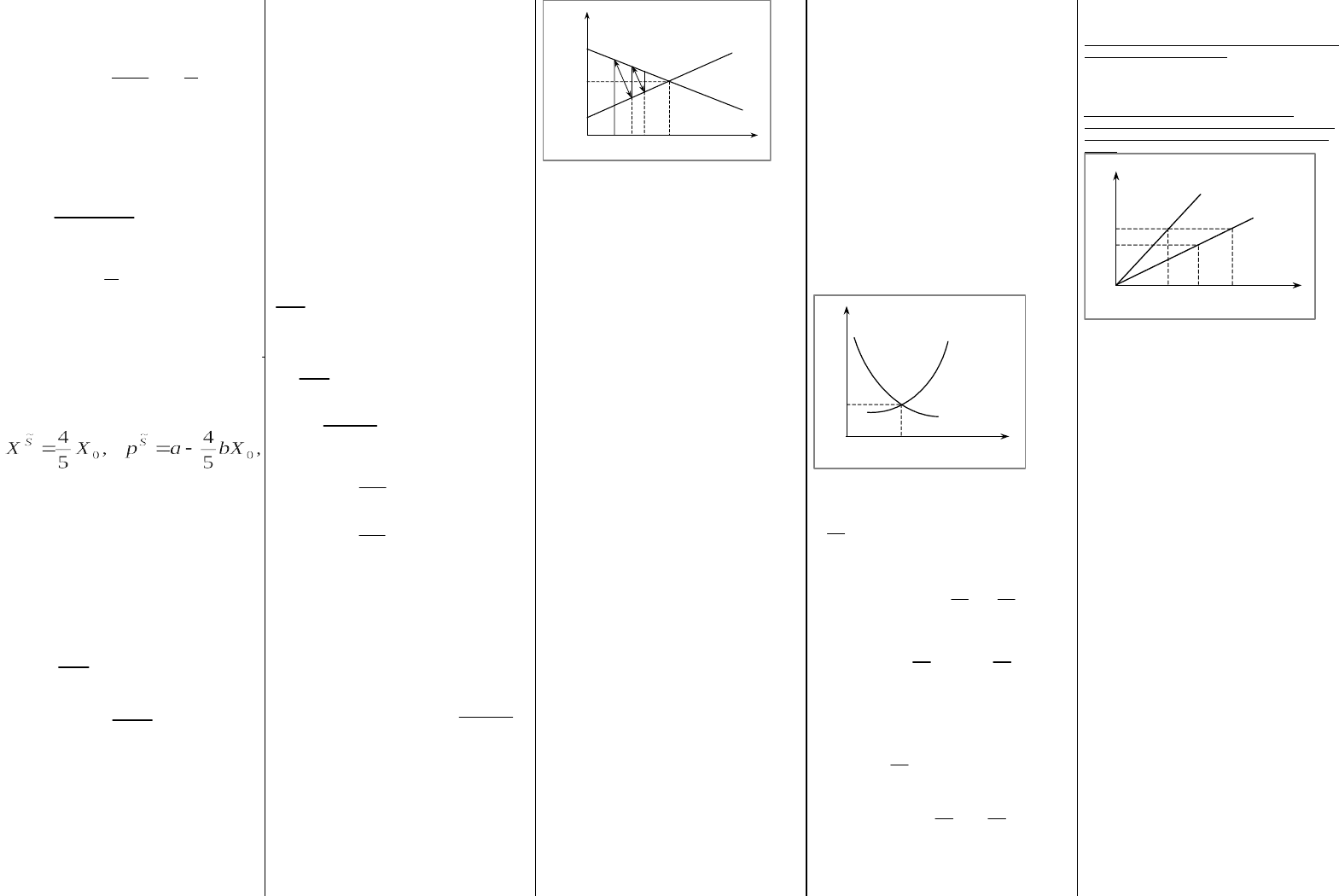
то есть выпуск больший, а цена низшая, чем в точке

Курно (потребителям это выгодно).

2. Если и вторая фирма так же, как и первая, будет действовать

за Стакельбергом, то есть исходя из того, что первая действует

в соответствии с Курно

















, то

получим ситуацию, которая имеет название

неравновесная за Стакельбергом.

В этом случае стратегии симметричные, поэтому за

одинаковых функций затрат

XX 

итак, (8.29) наберет вида:

2/3





Отсюда

XXX



За этих предположений прибыль обоих фирм окажется

меньшим, чем в точке Курно:

 dbXd

XXXX

SSSS 2

),(),(

).,(),(

212211

KKKK

XXXX 

Общий выпуск и цена в этом случае будут равняться:

то есть этой еще большей мерой подходит потребителю,

чем в точке равновесия за Стакельбергом, так как выпуск

(предложение) возрастает, а цены снижаются.

3. Если фирмы объединятся ли договорятся о

максимальной прибыли, то будет идтись об образовании

монополии. За этих предположений максимальная

суммарная прибыль можно подать так:

]2)([max

dXXbX



или, беря производную за Х (Х = Х

+ Х

— общий выпуск

монопольного объединения), получим:

– 2bX

= 0,

отсюда общий выпуск равняется:



цена:



то есть выпуск существенно уменьшится, а цена

существенно возрастет сравнительно с точкой Курно и

Стакельберга.

Итак, образование монополии - это наиболее плохой

вариант для потребителя.

18. ВОПРОС 18. Модели взаимодействия

потребителей и производителей. Модель Эванса.

Имеем рынок одного товара. Время t будем считать

непрерывной.

Обозначим через d = d(t) = [p(t)], s = s(t) = [p(t)]

інтегрований попит і пропозицію в момент t, а через p(t)

— цену товара в этот момент.

В модели постулюється, что спрос и предложение есть

линейными функциями цены:

(p) = a – bp, a > 0, b > 0 (спрос с возрастанием цены

спадает);

(p) =  + p,  > 0,  > 0 (предложение с возрастанием цены

возрастает).

Окрім цього, слушно вважати, що a >  (за нулевой цены

спрос превышает предложение).

Основная гипотеза модели состоит в том, что

изменение цены пропорциональная превышению спроса

над предложением

p =  (d – s)t,  > 0. (9.1)

В соответствии с гипотезой (9.1) взаимодействие

потребителей и производителей происходит таким чином,

что цена, которое отображает это взаимодействие,

неперервно приспосабливается к ситуации на рынке: за

превышение спроса над предложением цена возрастает, в

противоположном разе - спадает.

Используя сделанные предположения, можно прийти к

такому дифференционному уравнению относительно

цены:

.)0(,)(

ppapb



(9.2)

Это уравнение имеет стационарную (равновесную) точку р

(если

0









(9.3)

Из выражения (9.2) видно, что за

,0,



а за

,0,



поэтому

)(lim ptp





(в первом случае цена

достигает равновесного значения, возрастая, а в второй -

спадая, при этом равновесная цена р

не зависит от

начальной р

). Равновесная цена есть абсциссой точки

пересечения прямых спроса и предложения, то есть за

такой цены спрос равняется предложения.

Эти выводы получены без розв'язку уравнения (9.2). Они

будут такими самыми, если прямо использовать розв'язок

этого уравнения:

].1[)(

)()(

tbtb

eptp











Дискретный аналог модели Еванса представлен на рис.

9.1, где изображенные прямые интегрированного спроса и

предложения и показан механизм возникновения

последовательности p

, что возрастает от начальной цены

, за которой спрос не равняется предложения. Время

распределено на интервалы t, цена в момент

tnt 

равняется:

1111

)()(,





nnnnn

pbatpp

Ф(p)

= d

D, S

Ψ(p)

Рис. 9.1. Дискретный аналог модели Эванса

19. ВОПРОС 19. Модели взаимодействия

потребителей и производителей. Модель Вальраса.

Это модель идеального рынка с условием отсутствия

трансакционных издержек. Кроме того, в модели

отсутствует фактор времени, и сделки совершаются

только с уже произведенными товарами. Абстрактный

Аукционист, имея информацию обо всем рынке товаров,

объявляет цены, повышая их на товары избыточного

спроса и снижая на избыточное предложение. По этим

равновесным ценам и происходит прямой обмен

товарами, а отсутствие трансакционных издержек и

фактора времени делает участие денег в таком

товарообмене бессмысленным.

Модель Л. Вальраса представляет собой систему

линейных уравнений, где для каждого товара выделяется

отдельное уравнение. Поскольку с практической точки

зрения вряд ли возможно решение этой системы

уравнений, модель Вальраса носит теоретический

характер, показывает экономическую систему в идеале.

Основную роль в системе Вальраса играют равновесные

цены, т.е. цены, обеспечивающие равенство спроса и

предложения для каждого товара. Таким образом, его

модель, являясь по форме макроэкономической,

опирается на микроэкономические показатели.

20. ВОПРОС 20. Традиционные макроэкономические

модели.

Такие модели часто называют кейнсианскими, поскольку

в основе их конструкции заложена идея о невозможности

объяснить поведение рынка при помощи цен, по крайней

мере, в течение короткого периода. Эти модели

описываются системами из большого числа нелинейных

уравнений, составленными в соответствии с

теоретическими и эмпирическими гипотезами.

Теоретические просчеты могут вносить существенный

вклад в неточность прогноза. Например, в ряде случаев

историческая динамика макроэкономических показателей

хорошо укладывается в рамки модели, но в будущем

совпадение нарушается.

Прогноз, полученный при помощи больших

кейнсианских моделей, как правило, нуждается в

модификации. Это делается для того, что бы учесть

факторы, не входящие в спецификацию модели. Чтобы

скорректировать прогноз аналитики используют

добавочные факторы. Например, в приложении к

недавнему прогнозу компании Data Resources,

являющейся ведущим поставщиком эконометрических

услуг и использующей кейнсианскую модель, было

приведено около 10 тысяч (!) потенциальных добавочных

факторов.

За последние годы была выявлена масса недостатков

традиционных кейнсианских моделей и методов их

устранения. Но, тем не менее, многие из них по-прежнему

основываются на спорных фактах, например, на

инертности изменения цены.

21. ВОПРОС 21.Классическая модель рыночной

экономики. Рынок рабочей силы. Рынок денег. Рынок

товаров.

Классическую модель рыночной экономики можно

рассматривать как систему взаимосвязанных моделей,

любая из которых отбивает поведение одного из трех

рынков: рабочей силы, денег, товаров.

Модель наибольшее подходит для описания экономики с

совершенной конкуренцией. В условиях

функционирования монополий она не работает.

Рынок рабочей силы

Этот рынок, как и другие, описывается с помощью трех

зависимостей: функции спроса, функции предложения и

условия равновесия. В классической модели функция

спроса на рабочую силу выводится с таких двух гипотез:

1) предприятия (фирмы) полностью есть конкурентными

при наличии предложения товаров и найму рабочей силы;

2) за остатки равных условий предельный продукт работы

снижается с возрастанием объемов рабочей силы.

Предложение рабочей силы также выступает в функции

от реальной заработной платы.

Допускает постулат: чем большей будет реальная

заработная плата, тим большей будет и предложение

рабочей силы.

Эта гипотеза классической теории относительно рынка

рабочей силы представленная на рис. 12.1, на котором LD

- кривая спроса, а L

— кривая предложения.

Рис. 12.1

В равновесии реальная заработная плата равняется













, а занятость — L

Если бы реальная заработная плата превышала

равновесное значение, то есть















, это

возникло бы превышение предложения над спросом на

рабочую силу



























, поэтому

избыточное предложение привело бы к снижению

заработной платы w под влиянием вынужденной

безработицы, за этого условия цены будут снижаться, но

меньшей мерой, итак, реальная заработная плата

уменьшится к













Если же оказалось бы, что















, это

недостаток рабочей силы принудил бы предпринимателей

увеличить оплату работы, и снова было бы достигнутое

динамическое равновесие.

Рынок денег

Теория спроса на деньги (не учитывая другие виды

финансовых активов) в классической модели грунтуется

на гипотезе, за которой совокупный спрос на деньги - это

функция денежного дохода (то есть f (Y

), где Y —

валовий внутренний продукт в натуральном выражении,

pN— цена), эта функция (f) — линейная и прямо

пропорциональная денежному доходу:

= k Y

где предложение денег M

рассматривается как

фиксированная величина, екзогенно задана. На рис. 12.2

изображенные линии спроса и предложения денег. Для

любого Y своя кривая спроса (12.3).

Рис. 12.2

Если за фиксированного Y цена p < p

, это имеющееся

избыточное предложение денег M

– M

(p) > 0, в этом

случае допускает гипотеза, за которой цены возрастут к

уровню p

Рынок товаров

Спрос на товары (планированные затраты) - это сумма

спроса на потребительские и инвестиционные товары E =

C + I. В соответствии с моделью С = C(r), І = I(r) как

функции нормы процента r, снижаются с возрастанием r.

В самом деле, чем большее r, тем большим будет доход от

сбережения, итак, все более большая часть доходов будет

сохраняться, а меньшая (С) - будет расходоваться на

потребительские товары. Относительно инвестиций (І), то

чем большим есть r (то есть ставка процента, который

используется во время дисконтування будущих затрат и

доходов при инвестировании и приведении их к текущему

времени), тим низшей будет сегодняшняя оценка чистой

настоящей стоимости проекта.

В классической модели спрос на товары выступает в

функции уровня занятости, которая определяется на

рынке рабочей силы Y = Y (L

Условие равновесия состоит в потому, что предложение

товаров Y (L

) равняется спросу на товары E = C (r) +

I (r).

22. ВОПРОС 22. Модель Кейнса.

Английский экономист Дж.М. Кейнс вывел модель

макроэкономического равновесия, основанного на связи

между совокупными доходами и расходами. В этой

модели макроэкономическое равновесие существует, если

совокупные расходы равны стоимости текущего

производства (продукции):

Вся произведенная продукция/Реальный ВНП =

(Планируемые П+Г+И+ЧЭ)/Планируемые совокупные

расходы,

где П — потребительские расходы; Г —

правительственные расходы; И — инвестиции; ЧЭ —

чистый экспорт; ВНП — валовый национальный продукт.

Основными инструментами регулирования в модели

Кейнса были государственный бюджет, дефицитное

финансирование экономики, а также манипулирование

учетной ставкой процента. Целевые приоритеты модели

Кейнса - занятость и стабильность экономического роста,

а инструменты - государственный бюджет и кредитно-

денежная политика. Кейнс и его последователи исходят

из того, что чисто рыночный механизм не в состоянии

обеспечить стабильный экономический рост и полную

Моделирование окончательное

занятость, и именно поэтому требуется вмешательство

государства. Доктрина Кейнса нашла наиболее полное

применение в США, показав нам хорошую

результативность.

23. ВОПРОС 23. Односекторные нелинейные модели

макроэкономики. Модель Слоу.

Малосекторні нелинейные модели используются для

изучения долгосрочных тенденций и факторов развития

(трансформации) экономики. Небольшое количество

секторов разрешает аналитически подать и

проанализировать на модели развитие экономики с

адекватным учетом нелинейных зависимостей объемов

выпуска секторов от объемов ресурсов за разных

значений экзогенных параметров и на основании этого

получить некоторую обобщенную картину

экономического возрастания.

Модель Солоу есть односекторной моделью

экономического развития. В этой модели экономическая

система рассматривается как единое целое, вырабатывая

лишь один обобщенный продукт, который может и

потребляться, и инвестироваться. Модель довольно

адекватно отбивает важнейшие макроэкономические

аспекты процесса воспроизведение. Экспорт-импорт в

явном виде не учитываются1.

Состояние экономики в модели Солоу задается пятью

эндогенными сменными: X - валовой общественный

продукт (ВОП), C - фонд непроизводственного

потребления, І - инвестиции, L - количество занятых, K -

производственные фонды. Кроме этого, в модели

фигурируют такие экзогенные (что задаются вне

системы) показатели: v — годовой темп прироста

численности занятых,  — частица выбывших на

протяжении года основных производственных фондов, a

— коэффициент прямых затрат (частица промежуточного

продукта в валовом внутреннем продукте),  — норма

накопления (частица валовых инвестиций в ВВП).

Границы экзогенных параметров:

.10

,10

,11









Робиться предположения, которые эндогенные сменные

изменяются в времени (аргумент t выпускается, но он, как

правило, присутствует присутствующим определением).

Экзогенные сменные считаются постоянными в времени.

Считается, вчастности, что норма накопления есть

управляющим параметром, то есть в некоторый

начальный момент времени t

N=N0 она может

устанавливаться управляющим органом системы на

любом уровне в границах области допустимых значений.

Время t считают непрерывным и таким, что измеряется в

годах. Для мгновенных показателей LN=NL(t), KN=NK(t) это

есть довольно естественным, поскольку, в принципе,

любого дня можно узнать о численности занятых и путем

инвентаризации установить объем основных

производственных фондов. Значение показателей типа

потока XN=NX(t), IN=NI(t), CN=NC(t) в момент времени

tN=N[t]N+N{t} определяется в виде накопленных на

протяжении года, который начинается на 365{t} светал

более поздний 1 января года [t].

Делается предположение, которое годовой выпуск в

каждый момент времени определяется линейно-

однородной неоклассической производственной

функцией от двух сменных (ресурсов) K и L.

 

.,LKFX 

Вопросы

1. Особенности, принципы математического

моделирования

2. Особенности математического моделирования

экономики.

3. Этапы экономико-математического моделирования

4. Основные характеристики экономико-математических

моделей.

5. Общее понятие производственной функции.

6. Экономическое содержание производственной

функции.

7. Общая характеристика и этапы построения

производственных функций.

8. Виды производственных функций (производственные

функции Леонтьева, Кобба-Дугласа, линейная).

9. Экономико-математическая модель межотраслевого

баланса (модель Леонтьева «затраты-выпуск»).

10. Функция полезности.

11. Преимущества потребителя и его функция

полезности.

12. Модель поведения потребителя.

13. Уравнение Слуцкого (модель поведения потребителя).

14. Модель фирмы (модель поведения производителей)

15. Модель поведения фирмы на конкурентных рынках

(два конкурента).

16. Равновесие по Курно (модель поведения фирмы на

конкурентных рынках).

17. Равновесие и неравновесие по Стакельбергу (модель

поведения фирмы на конкурентных рынках).

18. Модели взаимодействия потребителей и

производителей. Модель Эванса.

19. Модели взаимодействия потребителей и

производителей. Модель Вальраса.

20. Традиционные макроэкономические модели.

21. Классическая модель рыночной экономики. Рынок

рабочей силы. Рынок денег. Рынок товаров.

22. Модель Кейнса.

23. Односекторные нелинейные модели макроэкономики.

Модель Слоу.

Моделирование окончательное