Сметанина Р.Н. и другие. Теоретические основы электротехники
Подождите немного. Документ загружается.

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
71
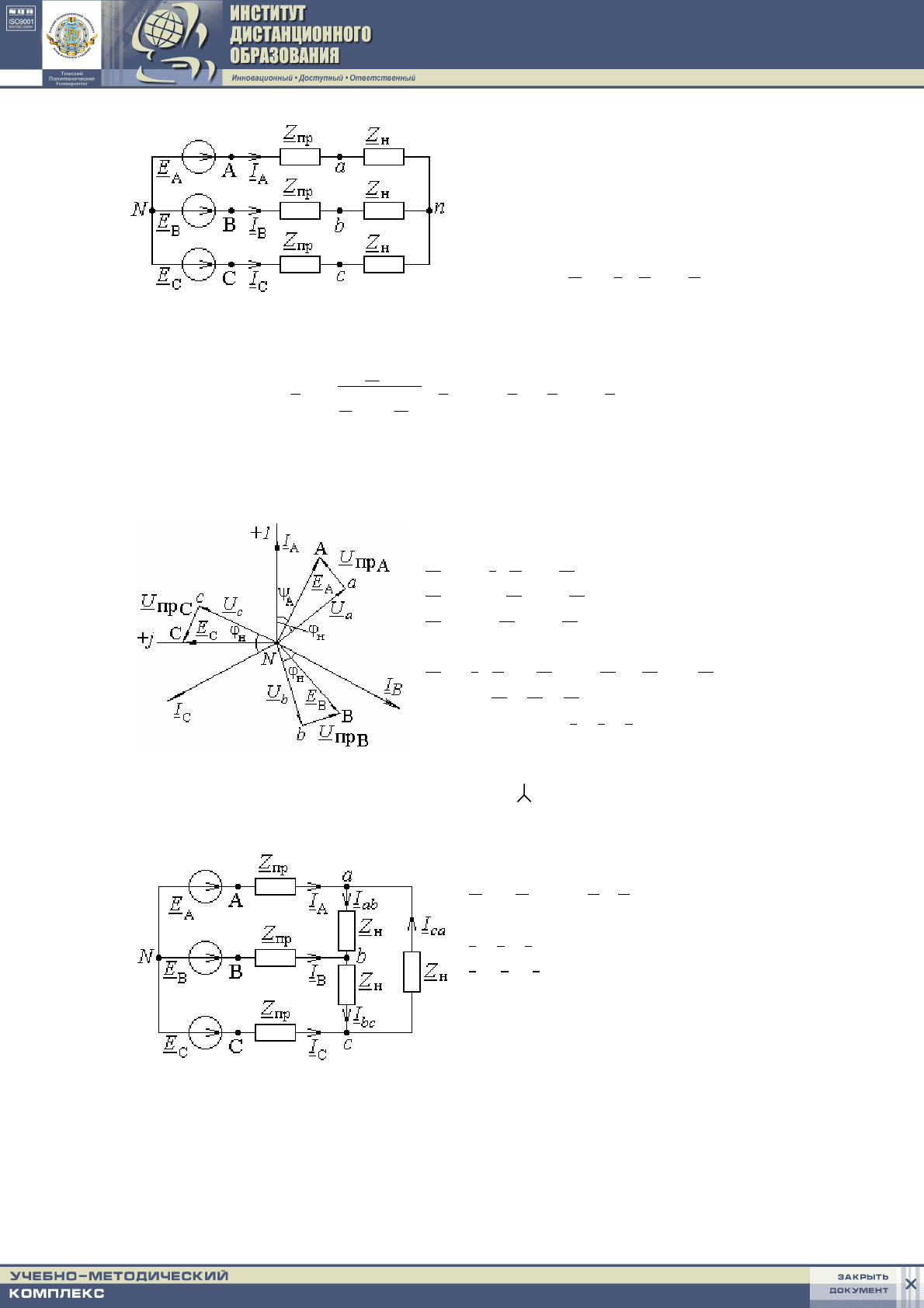
Схема 3
Расчет симметричной трехфазной
цепи достаточно провести для одной
фазы (любой), токи остальных фаз
определятся через оператор
a = е
j120°
.
По второму закону Кирхгофа для
одной фазы
Е
А
= I
А
(Z
пр
+ Z
н
), тогда
.
ACA
2
B
нпр
A
A
;;
Z
IaIIaI
Z
E
I ==
+
= .
Векторная диаграмма
токов и напряжений
Падения напряжения в линейных про-
водах:
U
прА
= I
А
Z
пр
= U
Aa
,
U
прB
= a
2
U
прA
= U
Bb
,
U
прC
= aU
прA
= U
Cc
.
Фазные напряжения нагрузок:
U
а
= I
A
Z
н
, U
b
= a
2
U
a
, U
c
= aU
a
; напря-
жения
U
a
, U
b
, U
c
сдвинуты относитель-
но своих токов
I
A
, I
B
, I
C
на угол ϕ
н
.
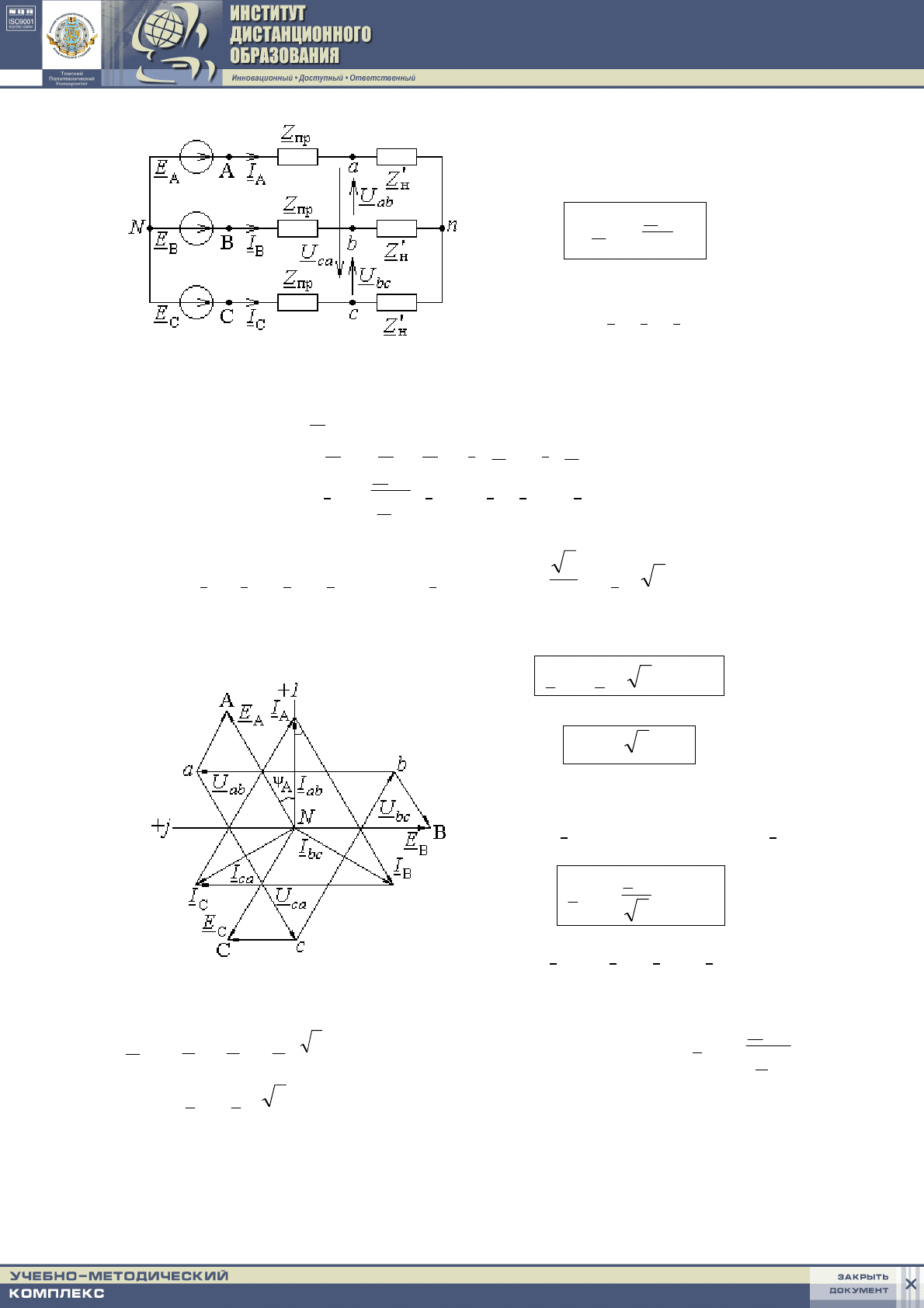
2. Соединение “звезда – треугольник” ( –
Δ).
Схема 4
Известно:
Е
А
= Е
А
е
jψ
А
, Z
н
, Z
пр
.
Рассчитать токи:
I
А
, I
B
, I
C
– линейные;
I
ab
, I
bc
, I
ca
– фазные.
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
72
Схема 5
Преобразуем “треугольник” abc
в эквивалентную “звезду” сопро-
тивлений:
Получилась схема 5, расчет ли-
нейных токов
I
A
, I
B
, I
C
рассмотрен
в п. 6.3.1.
3
н
н
Z
Z =
'
.
По линейным токам определим фазные, предварительно определив
фазное напряжение
U
аb
по II закону Кирхгофа:
U
аb
= U
а
– U
b
= I
А
'
н
Z
– I
B
'
н
Z
;
I
аb
=
н
Z
U
ab
, I
bc
= a
2
I
ab
; I
ca
= aI
ab
,
тогда для узла “а” по I закону Кирхгофа определим линейный ток
I
А
= I
аb
– I
ca
= I
ab
(1 – a) = I
ab
(1 + 0,5 – j
2
3
) = I
ab
3 е
–j30°
.
Векторная диаграмма
токов и напряжений
Для симметричной нагрузки
o
30
A
3
j
ab
eII
−
=
;
фл
3 II =
.
Следовательно, рассчитав линей-
ный ток
I
А
, определим фазный I
ab
:
o
30
A
3
j
ab
e
I
I = ;
I
bc
= a
2
I
ab
; I
ca
= aI
ab
.
Если в схеме 4
Z
пр
= 0, тогда линейные напряжения равны фазным
напряжениям на нагрузках. Определив линейное напряжение
o
30
ABA
AB
3
j
eEEEU ⋅=−=
(§ 6.2), определим фазный ток
н
AB
Z
U
I
ab
=
;
тогда
o
30
3
j
abA
eII
−
⋅= (§ 6.3.1). Остальные фазные и линейные токи
определяются через оператор
o
120j
ea
=
.
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
73
В трехфазной цепи построение векторных диаграмм следует начи-
нать с фазных ЭДС генератора
E
A
, E
B
и E
C
, которые всегда образуют
симметричную систему векторов. Таким образом, на диаграмме получа-
ем положение точек
A, B, C и N. Затем строим векторы U
Aa
, U
Bb
, U
Cc
под
своими углами относительно положительной действительной оси ком-
плексной плоскости, направляя их соответственно в точки
A, B, C. В ре-
зультате получим точки
a, b, c.
Для схемы 3 остается соединить точки
a, b, c с точкой N и получим
фазные напряжения нагрузки
U
a
, U
b
, U
c
.
Для схемы 4 нужно соединить точки
a, b, c и получим “треугольник”
фазных напряжений нагрузки, направив стрелки напряжений
U
ab
, U
bc
,
U
ca
соответственно в точки a, b, c.
В этих же осях строим лучевую диаграмму токов.
По диаграмме проверяем соответствие направления токов и напря-
жений характеру нагрузки (§ 3.7).
При соединении генератора “треугольником” (схема 2) достаточно
преобразовать линейные ЭДС в фазные:
Е
А
=
o
30
AB
3
j
e
E
−
, дальнейший
расчет аналогичен рассмотренному в § 6.3.1.
6.3.2. Несимметричная цепь
Несимметричная трехфазная цепь имеет разные комплексные сопро-
тивления фаз. Рассмотрим особенности расчета несимметричной цепи,
соединение “звезда–звезда” ( – ).
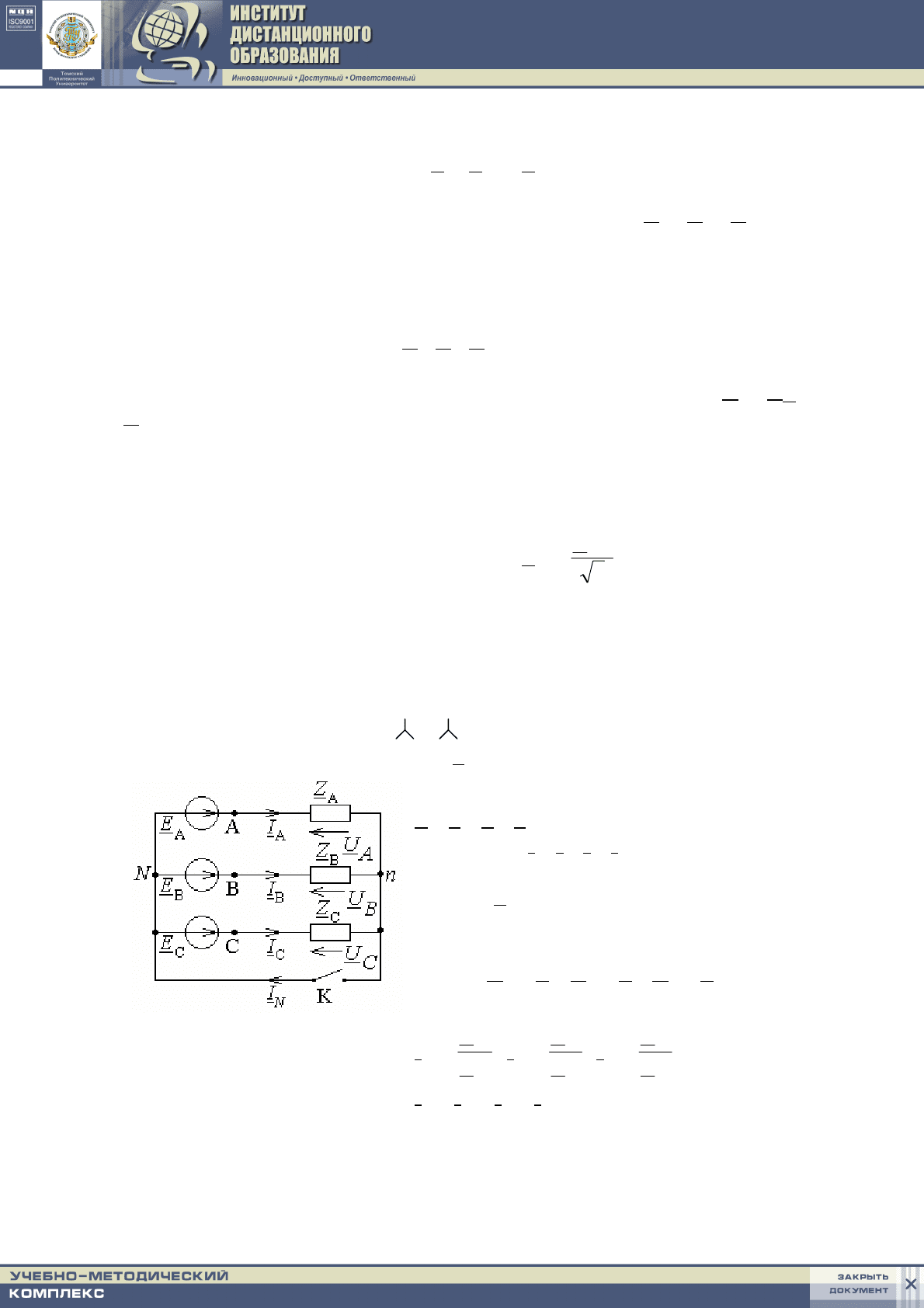
1.
С нулевым проводом, причем Z
N
= 0 (ключ “К” замкнут).
Схема 6
Известно:
Е
А
, Z
А
, Z
B
, Z
C
.
Рассчитать:
I
А
, I
B
, I
C
, I
N
.
___________________________________
Так как
Z
N
= 0, то ϕ
N
= ϕ
n
, U
N
= 0, следо-
вательно, фазные напряжения нагрузок
равны фазным ЭДС, т. е.
U
А
= E
A
; U
В
= E
В
; U
С
= E
С
,
тогда
I
А
=
A
A
Z
E
; I
В
=
B
B
Z
E
; I
C
=
C
C
Z
E
;
I
N
= I
А
+ I
B
+ I
C
.

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
74
2.
Без нулевого провода, Z
N
= ∞, ϕ
N
≠ ϕ
n
, U
N
≠ 0 (ключ “K” разомкнут).
U
N
рассчитаем по методу узловых потенциалов, приняв ϕ
N
= 0 (§ 3.4):
U
N
=
CBA
CCBBAA
YYY
YEYEYE
++
+
+
.
Токи рассчитываем по обобщенному закону Ома:
I
А
= (Е
А
– U
N
)Y
А
; I
B
= (Е
B
– U
N
)Y
B
; I
C
= (Е
C
– U
N
)Y
C
.
Фазные напряжения нагрузки:
U
A
= E
A
– U
N
, U
B
= E
B
– U
N
, U
C
= E
C
– U
N
.
Векторные диаграммы
1.
С нулевым проводом:
I
N
= I
А
+ I
B
+ I
C
2.
Без нулевого провода:
I
А
+
I
B
+
I
C
= 0
Вывод:
нулевой провод выравнивает фазные напряжения нагрузок
при несимметричной нагрузке. При несимметричной нагрузке и отклю-
ченном нулевом проводе происходит смещение нейтральной точки на-
грузки
n, что характеризуется величиной U
N
. Это приводит к несиммет-
рии фазных напряжений на нагрузке
U
A
, U
B
, U
C
. Чем больше Z
N
, тем
больше
U
N
, тем возможно большая несимметрия фазных напряжений.
Рассмотрим особенности расчета несимметричной цепи при соеди-
нении нагрузки “треугольником”.
1.
При заданных линейных напряжениях U
AB
, U
BC
, U
CA
, когда ком-
плексные сопротивления линейных проводов равны нулю, т. е.
0
пр
=Z.
Схема 7
При соединении трехфазной цепи
треугольником следует помнить, что
если сопротивления линейных про-
водов равны 0, то линейные напря-
жения
U
AB
, U
BC
, U
CA
являются одно-
временно фазными напряжениями
нагрузки. Поэтому фазные токи лег-
ко определить по закону Ома для
участка цепи:
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
75
CA
CA
CA
BC
BC
BC
AB
AB
AB
;;
Z
U
I
Z
U
I
Z
U
I ===
. (*)
А линейные токи определяются по I закону Кирхгофа:
I
A
= I
AB
– I
BC
; I
B
= I
BC
– I
AB
; I
C
= I
CA
– I
BC
.
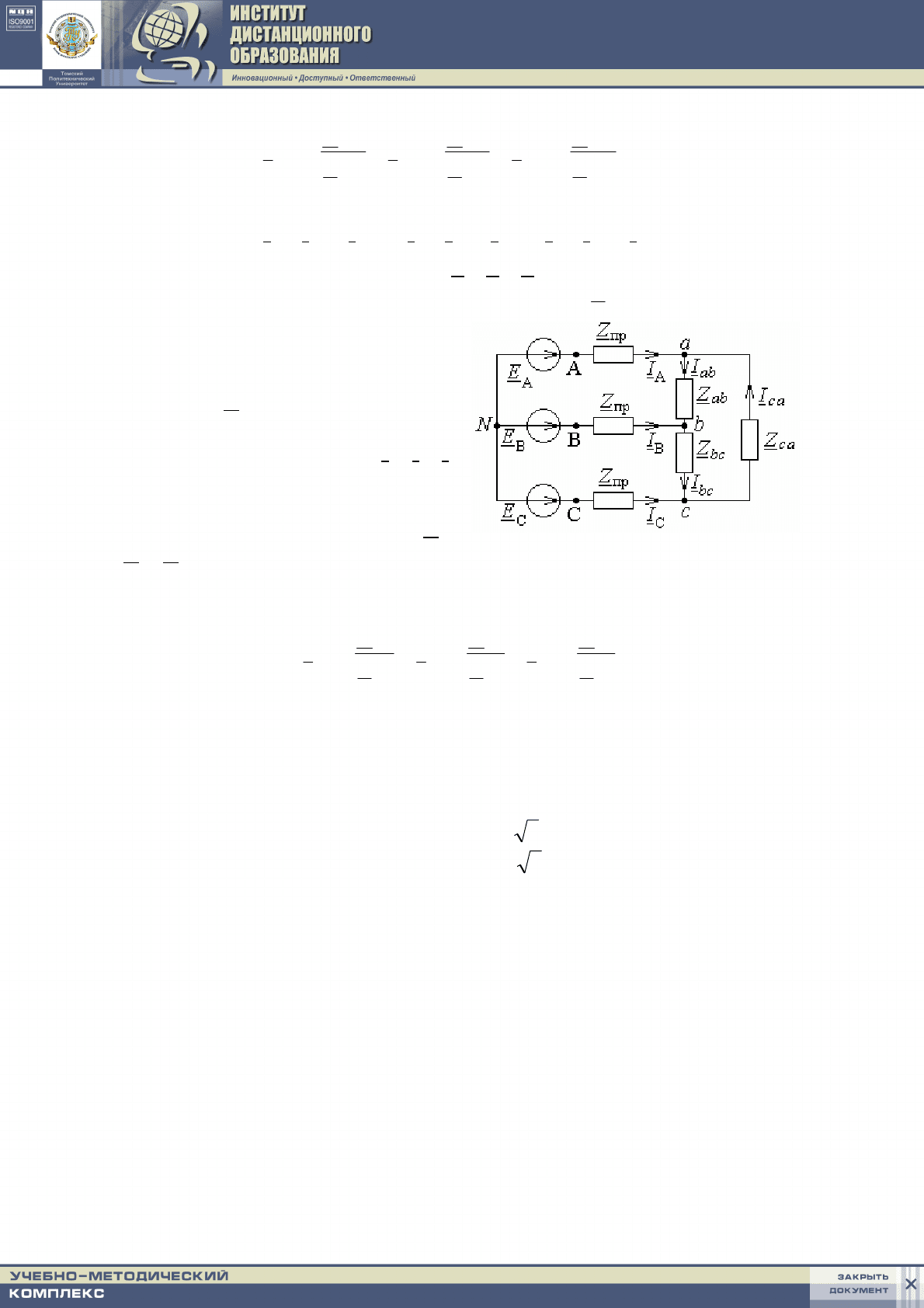
2.
При заданных фазных ЭДС Е
A
, Е
B
, Е
C
, когда комплексные сопро-
тивления линейных проводов неравны нулю, т. е.
0
пр
≠
Z, необходимо:
а) преобразовать “треугольник”
abc в эквивалентную “звезду” и
рассчитать напряжение смещения
нейтралей
U
N
(§ 6.3.2);
б) по обобщенному закону Ома
рассчитать линейные токи
I
A
, I
B
, I
C
(§ 6.3.2);
в) по второму закону Кирхгофа
рассчитать фазные напряжения
U
ab
,
U
bc
, U
ca
(§ 6.3.1, п. 2);
г) по закону Ома рассчитать
фазные токи нагрузки:
ca
ca
bc
bc
bc
ab
ab
ab
Z
U
I
Z
U
I
Z
U
I ===
ca
;;.
6.4. Мощность трехфазной цепи
6.4.1. Симметричная цепь
Р
u
= 3Р
ф
= 3Е
ф
I
ф
cosϕ = 3 U
л
I
л
cosϕ;
Q
u
= 3Q
ф
= 3Е
ф
I
ф
sinϕ = 3 U
л
I
л
sinϕ.
6.4.2. Несимметричная цепь
Р
u
= Е
A
I
A
cosϕ
A
+ E
B
I
B
cosϕ
B
+ E
C
I
C
cosϕ
C
;
Q
u
= Е
A
I
A
sinϕ
A
+ E
B
I
B
sinϕ
B
+ E
C
I
C
sinϕ
C
.
Мощности нагрузок
Р
п
и Q
п
рассчитываются, как в однофазной цепи.
Баланс мощностей записывается аналогично:
Р
u
= Р
п
; Q
u
= Q
п
.
Схема 8
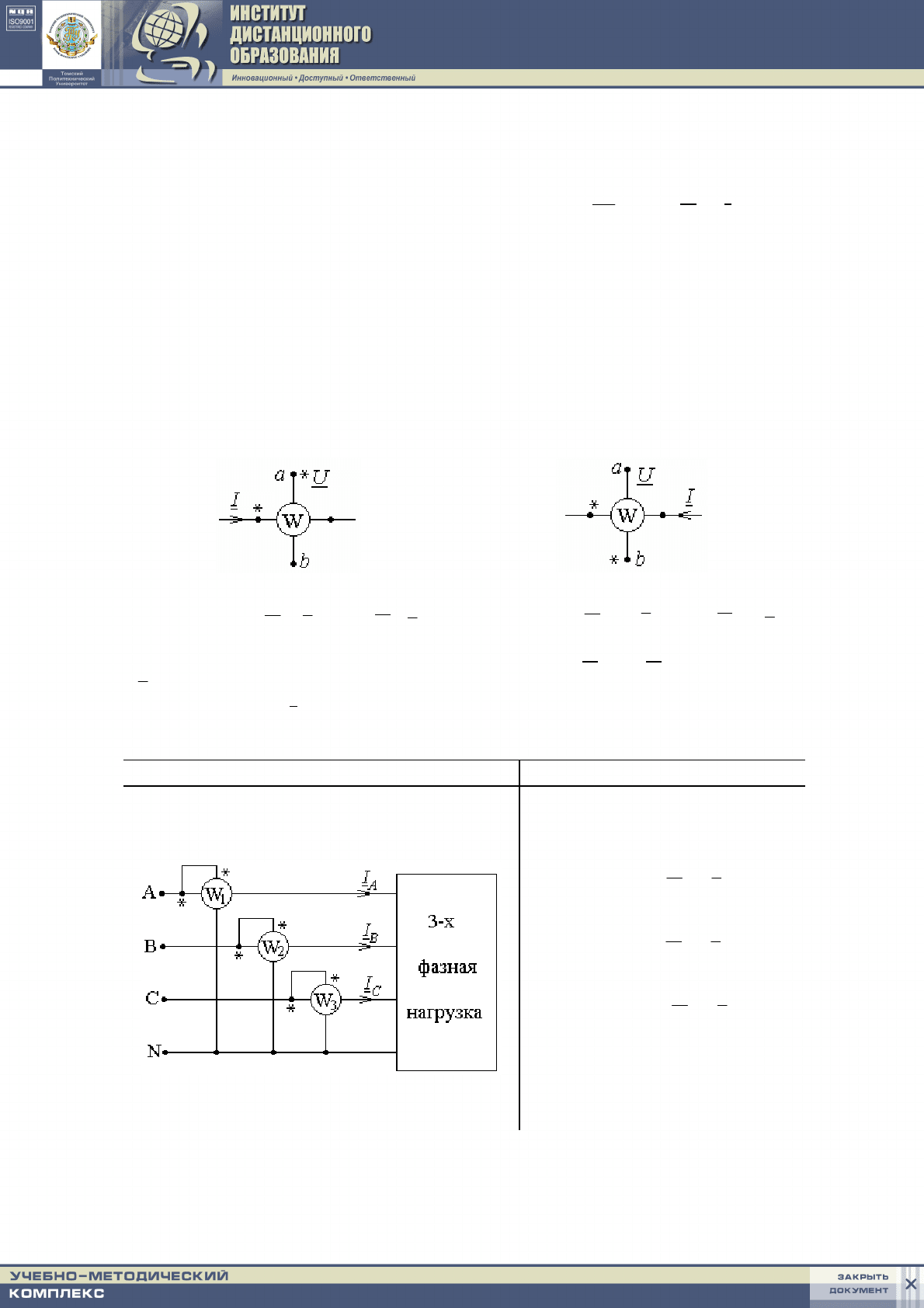
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
76
6.5. Измерение активной мощности трехфазной цепи
Активная мощность участка цепи P = UI cos
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∧
UI , где U и I – ком-
плексы действующих значений напряжения и тока участка цепи.
Для измерения активной мощности служит ваттметр, у которого две
обмотки: токовая – включается последовательно (как амперметр) и на-
пряжения – параллельно участку цепи (как вольтметр).
Одноименные зажимы ваттметра обозначают звездочками (*). При
записи показаний ваттметра следует обращать внимание на положение
звездочек по отношению к току или потенциалам схемы.
Рассмотрим два случая.
а)
P = U
ab
I cos
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∧
IU
ab
= Re(U
ab
∗
I
),
∗
I
– сопряженный комплекс тока.
б)
P = U
bа
I cos
⎥
⎦
⎤
⎢
⎣
⎡
−
∧
)( IU
ba
= Re[U
bа
(–
∗
I
)];
U
ba
= –U
аb
.
В уравнениях
I берется с плюсом, если на схеме стрелка тока входит
в одноименный зажим (*) (а), и с минусом, если ток выходит из зажима
(*) (б).
Схема Измеряемая мощность
1.
С нулевым проводом
Р = Р
1
+ Р
2
+ Р
3
=
=
U
А
I
А
cos
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∧
A
A
IU +
+
U
В
I
В
cos
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∧
B
B
IU
+
+
U
С
I
С
cos
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∧
C
C
IU .
Примечание. В случае сим-
метричной цепи достаточно
включить один ваттметр, а
результат утроить.
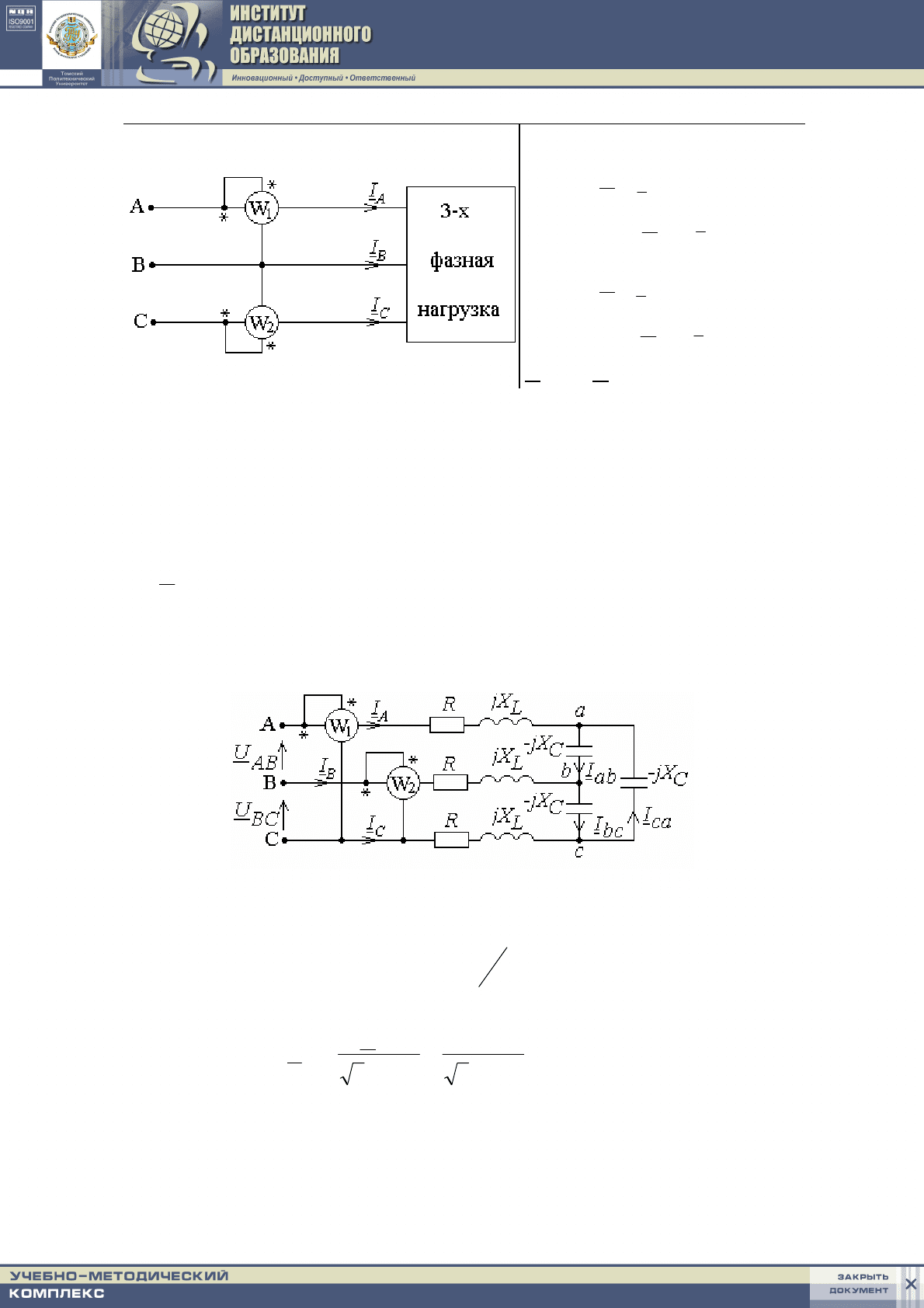
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
77
2.
Без нулевого провода
Р = Р
1
+ Р
2
,
Р
1
= Re(U
АВ
∗
I А
) =
=
U
АВ
I
А
cos
⎟
⎠
⎞
⎜
⎝
⎛
∧
A
AB
IU ;
Р
2
= Re(U
СВ
∗
I
С
) =
=
U
СВ
I
С
cos
⎟
⎠
⎞
⎜
⎝
⎛
∧
C
CB
IU ;
U
СВ
= –U
ВС
.
Возможны две другие схемы включения ваттметров.
Примечание. В случае симметричной цепи достаточно включить
один ваттметр, а результат удвоить.
Пример 1
В симметричной трехфазной цепи известно:
o
60
AB
173
j
eU = В; R = 25 Ом;
X
L
= 24 Ом; X
С
= 72 Ом.
Определить показания ваттметров, активную потребляемую цепью
мощность и напряжение
u
ab
(t) между точками a и b .
Решение
1. Преобразуем “треугольник” сопротивлений abc в эквивалентную
«звезду» с сопротивлениями
24
3
'
==
C
C
X
X
Ом.
2. По заданному линейному напряжению найдем фазную ЭДС:
o
o
o
o
30
30
60
30
AB
A
100
3
173
3
j
j
j
j
e
e
e
e
U
E =
⋅
=
⋅
= В.
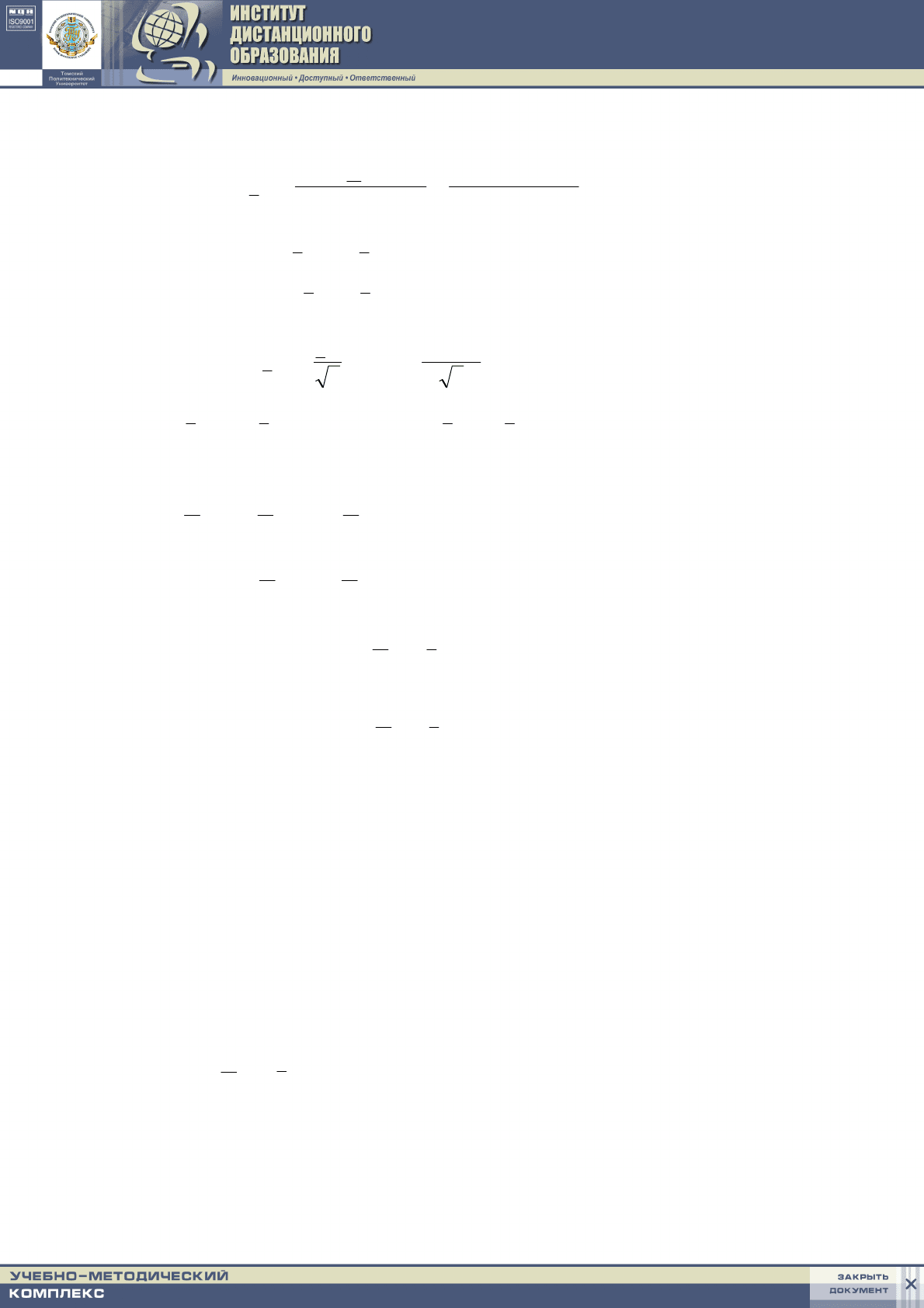
Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
78
3. Найдем линейные токи:
o
o
30
30
'
C
A
A
4
242425
100
j
j
L
e
jj
e
jXjXR
E
I =
−+
=
−+
=
А;
ooo
9030120
A
2
B
44
jjj
eeeIaI
−−
=⋅== А;
ooo
15030120
AC
44
jjj
eeeIaI =⋅== А.
4. Определим фазные токи “треугольника”
abc:
oo
o
o
6030
30
30
31,2
3
4
3
jj
j
j
A
ab
ee
e
e
I
I =⋅=⋅= A;
o
602
31,2
j
abbc
eIaI
−
== A; 31,231,2
180
−===
o
j
abca
eIaI A.
5. Найдем приложенные к ваттметрам напряжения:
а) к первому ваттметру –
173173173
18060120
ABCAAC
=−=⋅−=−=−=
ooo
jjj
eeeUaUU
В;
б) ко второму ваттметру –
ooo
6060120
AB
2
BC
173173
jjj
eeeUaU
−−
=⋅==
В.
6. Определим показания ваттметров:
=ψ−ψ⋅⋅=⋅⋅=
∧
)cos()cos(
AACAAC
A
AC
AAC1
IUIUIUP
600)300cos(4173 =−⋅⋅=
o
Вт;
=ψ−ψ⋅⋅=⋅⋅=
∧
)cos()cos(
BBCBBC
B
BC
BBC2
IUIUIUP
600)9060cos(4173
=+−⋅⋅=
o
Вт,
тогда сумма показаний ваттметров равна 1200600600
21
=
+
=
+
=
PPP Вт.
7. Найдем активную потребляемую цепью мощность:
12002543)(3
22
AП
=⋅⋅== RIР Вт,
т. е. расчет проведен верно, т. к.
Р=Р
1
+Р
2
=Р
П
.
Действительно, для измерения активной мощности симметрич-
ной трехфазной цепи, достаточно включить один ваттметр и удво-
ить его показание.
8. Найдем мгновенное значение напряжения u
ab
(t) между точками a и b:
а) комплекс этого напряжения можно рассчитать по закону Ома
ooo
309060
C
3,1667231,2)(
jjj
ab
ab
eeejXIU
−−
=⋅=−⋅= В;
б) комплекс этого напряжения можно рассчитать по второму за-
кону Кирхгофа

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
79
=−⋅−=−⋅−−⋅= )()()()(
'
C
BA
'
C
B
'
C
A
jXIIjXIjXIU
ab
ooo
309030
3,16683144)24()4246,3()24()44(
jjj
ejjjjjee
−−
=−=−⋅++=−⋅−=
В;
в) в результате мгновенное значение искомого напряжения равно
)30sin(5,234)30sin(23,166)(
oo
−ω=−ω= tttu
ab
В.
Пример 2
К симметричному трехфазно-
му генератору подключена на-
грузка, соединенная «звездой».
Токи во всех фазах одинаковы
по 1 A;
E
ф
= 100 В.
Определить показание ватт-
метра.
Решение
Показания ваттметра
()
⎥
⎦
⎤
⎢
⎣
⎡
−=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
∧
N
N
N
W
IUIUIUP
AB
AB
*
AB
cosRe .
Знак (–) означает, что ток
I
N
выходит из зажима (*). Для определе-
ния тока
I
N
построим векторную диаграмму напряжений и токов, учи-
тывая, что нагрузка несимметричная. Сначала строим диаграмму фаз-
ных ЭДС.
Так как в схеме есть нулевой провод, в ко-
торый включен ваттметр, потенциалы точек
N
и
n одинаковы, поэтому строим токи I
A
, I
B
, I
C
относительно своих ЭДС, учитывая характер
нагрузки.
Ток в нулевом проводе определяем по I за-
кону Кирхгофа
I
N
=I
A
+I
B
+I
C
.
Сложение можно провести графически, построив векторы токов в
масштабе, а можно аналитически, записав комплексы токов
I
A
, I
B
, I
C
.
Для этого, выбрав оси комплексной плоскости, запишем каждый ток:

Теоретические основы электротехники. Ч. 1. Постоянный и синусоидаль-
ный токи в линейных цепях: учебное пособие / Р.Н. Сметанина, Г.В. Но-
сов, Ю.Н. Исаев. – 3-е изд., испр. – Томск: Изд-во ТПУ, 2009. – 118 с.
80
I
A
=1 A; I
B
=1
o
150j
e A; I
C
=1
o
150j
e
−
A.
Тогда
I
N
=1 + 1
o
150j
e +
o
150j
e
−
=1 –
A73,05,0
2
3
5,0
2
5
−=−−+ jj
.
Напряжение
U
AB
определим по формуле (§ 6.2) с учетом векторной диа-
граммы:
;3100
30
AB
o
j
eU =
–I
N
= 0,73 A; –
N
I
∗
=0,73 A.
Определяем показания ваттметра:
Вт11030cos73,0310073,03100Re
30
=⋅=
⎟
⎠
⎞
⎜
⎝
⎛
⋅=
o
o
j
W
eP .
Показание ваттметра равно 110 Bт.
Пример 3
Система фазных ЭДС симметрична:
E
ф
= 100 В; X
L
= X
C
= R = 50 Ом.
Определить показания приборов
электродинамической системы для двух
случаев:
1)
в исходной схеме;
2)
если произойдет обрыв провода
в точке М.
Полагать R
V
= ∞, R
A
= 0.
Решение
1. Расчет в исходной схеме.
Так как R
V
= ∞, следовательно, в цепи нет нулевого провода, а зна-
чит, произойдет смещение точки n относительно точки N, т. е. появится
напряжение U
N
.
Определим U
N
(уравнение § 6.3.2):
;
CBA
CCBBAA
YYY
YEYEYE
U
N
++
+
+
= E
A
= E; E
B
= a
2
E; E
C
= aE,
где
.
1
;
1
;
1
CBA
jY
jX
YY
R
YjY
jX
Y
CL
=
−
===−==
Определим
()
()
B.273366,2366,1
5,0
2
3
2
3
5,0
120
2
o
j
N
eEj
jjjE
jYYjY
aEjYEYajYE
U
−
=⋅−−=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−−⋅−−−⋅=
++−
++−
=
