Soong T.T. Fundamentals of Probability and Statistics for Engineers
Подождите немного. Документ загружается.

x
6.0
0.0
0.5
1.0
1.5
2.0
f
X
(
x
)
(a)
6.0
0.0
0.5
1.0
1.5
2.0
f
X
(
x
)
x
(b)
0.0 1.5 3.0
4.5
0.0
1.5
3.0
4.5
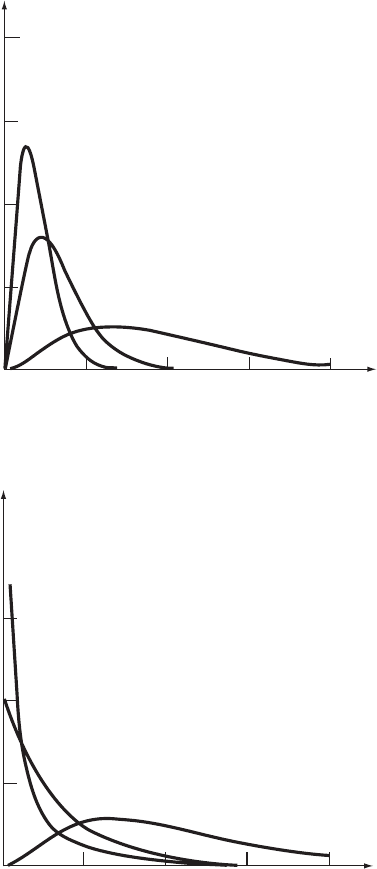
Figure 7.10 Gamma distribution with: (a) 3 and 5, 3, and 1, and
(b) 1 and 0 5, 1, and 3
214 Fundamentals of Probability and Statistics for Engineers
η
=3, λ =5
η
=3, λ =3
η
=3, λ =1
η
=0.5, λ =1
η
=1, λ =1
η =3, λ =1
:
TLFeBOOK

7.4.1 EXPONENTIAL DISTRIBUTION
When 1, the gamma density function given by Equation (7.52) reduces to
the exponential form
where is the parameter of the distribution. Its associated PDF, mean,
and variance are obtained from Equations (7.55) and (7.57) by setting 1.
They are
and
Among many of its applications, two broad classes stand out. First, we will
show that the exponential distribution describes interarrival time when arrivals
obey the Poisson distribution. It also plays a central role in reliability, where the
exponential distribution is one of the most important failure laws.
7.4.1.1 Interarrival Time
There is a very close tie between the Poisson and exponential distributions. Let
random variable X(0,t) be the number of arrivals in the time interval [0,t) and
assume that it is Poisson distributed. Our interest now is in the time between
two successive arrivals, which is, of course, also a random variable. Let this
interarrival time be denoted by T. Its probability distribution function, F
T
(t),
is, by definition,
In terms of X(0,t), the event T > t is equivalent to the event that there
are no arrivals during time interval [0, t), or X(0, t) 0. Hence, since
Some Important Continuous Distributions 215
f
X
x
e
x
; for x 0;
0; elsewhere;
(
7:58
(>0)
F
X
x
1 e
x
; for x 0;
0; elsewhere;
(
7:59
m
X
1
;
2
X
1
2
: 7:60
F
T
t
PT t1 PT > t; for t 0;
0; elsewhere:
(
7:61
TLFeBOOK

as given by Equation (6.40), we have
Comparing this expression with Equation (7.59), we can establish the result
that the interarrival time between Poisson arrivals has an exponential distribu-
tion; the parameter in the distribution of T is the mean arrival rate associated
with Poisson arrivals.
Example 7.6. Problem: referring to Example 6.11 (page 177), determine the
probability that the headway (spacing measured in time) between arriving
vehicles is at least 2 minutes. Also, compute the mean headway.
Answer: in Example 6.11, the parameter was estimated to be 4.16 vehicles
per minute. Hence, if T is the headway in minutes, we have
The mean headway is
Since interarrival times for Poisson arrivals are independent, the time required
for a total of n Poisson arrivals is a sum of n independent and exponentially
distributed random variables. Let T
j
, j 1, 2, . . . , n, be the interarrival time
between the (j 1)th and jth arrivals. The time required for a total of n arrivals,
denoted by X
n
,is
where T
j
,j 1,2,...,n, are independent and exponentially distributed with the
same parameter . In Example 4.16 (page 105), we showed that X
n
has a
gamma distribution with 2 when n 2. The same procedure immediately
shows that, for general n, X
n
is gamma-distributed with n. Thus, as stated,
the gamma distribution is appropriate for describing the time required for a
total of Poisson arrivals.
Example 7.7. Problem: ferries depart for trips across a river as soon as nine
vehicles are driven aboard. It is observed that vehicles arrive independently at
an average rate of 6 per hour. Determine the probability that the time between
trips will be less than 1 hour.
Answer: from our earlier discussion, the time between trips follows a gamma
distribution with 9 and 6. Hence, let X be the time between trips in
216
Fundamentals of Probability and Statistics for Engineers
P[X(0, t) 0] e
t
F
T
t
1 e
t
; for t 0;
0; elsewhere:
(
7:62
PT 2
Z
1
2
f
T
tdt 1 F
T
2e
24:16
0:00024:
m
T
1
1
4:16
minutes 0:24 minutes:
X
n
T
1
T
2
T
n
; 7:63
TLFeBOOK

hours; its density function and distribution function are given by Equations
(7.52) and (7.55). The desired result is, using Equation (7.55),
Now, (9) 8!, and the incomplete gamma function (9,6) can be obtained by
table lookup. We obtain:
An alternative computational procedure for determining P(X 1) inExample
7.7 can be found by noting from Equation (7.63) that random variable X can be
represented by a sum of independent random variables. Hence, according to
the central limit theorem, its distribution approaches that of a normal random
variable when is large. Thus, provided that is large, computations such as
that required in Example 7.7 can be carried out by using Table A.3 for normal
random variables. Let us again consider Example 7.7. Approximating X by
a normal random variable, the desired probability is [see Equation (7.25)]
where U is the standardized normal random variable. The mean and standard
deviation of X are, using Equations (7.57),
and
Hence, with the aid of Table A.3,
which is quite close to the answer obtained in Example 7.7.
Some Important Continuous Distributions 217
PX 1F
X
1
;
9; 6
9
:
PX 10:153:
PX 1'PU
1 m
X
X
;
m
X
9
6
3
2
;
X
1=2
3
6
1
2
:
PX 1'PU 1F
U
11 F
U
1
1 0:8413 0:159;
TLFeBOOK
7.4.1.2 Reliability and Exponential Failure Law
One can infer from our discussion on interarrival time that many analogous
situations can be treated by applying the exponential distribution. In reliability
studies, the time to failure for a physical component or a system is expected to
be exponentially distributed if the unit fails as soon as some single event, such
as malfunction of a component, occurs, assuming such events happen indepen-
dently. In order to gain more insight into failure processes, let us introduce
some basic notions in reliability.
Let random variable T be the time to failure of a component or system. It is
useful to consider a function that gives the probability of failure during a
small time increment, assuming that no failure occurred before that time. This
function, denoted by h(t), is called the hazard function or failure rate and is
defined by
which gives
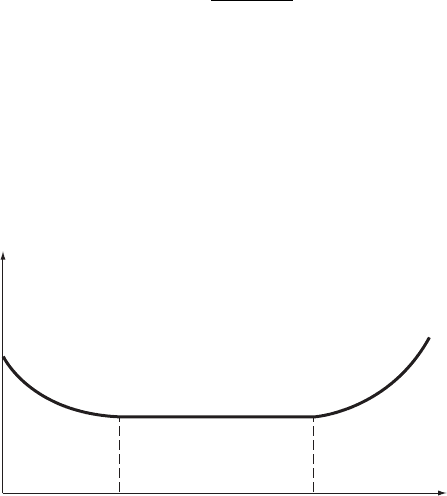
In reliability studies, a hazard function appropriate for many phenomena
takes the so-called ‘bathtub curve’, shown in Figure 7.11. The initial portion of
the curve represents ‘infant mortality’, attributable to component defects and
manufacturing imperfections. The relatively constant portion of the h(t) curve
represents the in-usage period in which failure is largely a result of chance
failure. Wear-out failure near the end of component life is shown as the
h
(
t
)
t
1
t
2
t
Figure 7.11 Typical shape of a hazard function
218 Fundamentals of Probability and Statistics for Engineers
htdt Pt < T t dtjT t7:64
ht
f
T
t
1 F
T
t
: 7: 65
TLFeBOOK
increasing portion of the h(t) curve. System reliability can be optimized by
initial ‘burn-in’until time t
1
to avoid premature failure and by part replacement
at time t
2
to avoid wear out.
We can now show that the exponential failure law is appropriate during the
‘in-usage’ period of a system’s normal life. Substituting
and
into Equation (7.65), we immediately have
We see from the above that parameter in the exponential distribution plays
the role of a (constant) failure rate.
We have seen in Example 7.7 that the gamma distribution is appropriate
to describe the time required for a total of arrivals. In the context of
failure laws, the gamma distribution can be thought of as a generalization of
the exponential failure law for systems that fail as soon as exactly events
fail, assuming events take place according to the Poisson law. Thus, the
gamma distribution is appropriate as a time-to-failure model for systems
having one operating unit and 1 standby units; these standby units go
into operation sequentially, and each one has an exponential time-to-failure
distribution.
7.4.2 CHI-SQUARED DISTRIBUTION
Another important special case of the gamma distribution is the chi-squared
(
2
) distribution, obtained by setting 1/2 and n/2 in Equation (7.52),
where n is a positive integer. The
2
distribution thus contains one parameter,
n, with pdf of the form
Some Important Continuous Distributions 219
f
T
te
t
; t 0;
F
T
t1 e
t
; t 0;
ht: 7:66
f
X
x
1
2
n=2
n=2
x
n=21
e
x=2
; for x 0;
0; elsewhere:
8
>
<
>
:
7:67
TLFeBOOK

The parameter n is generally referred to as the degrees of freedom. The utility of
this distribution arises from the fact that a sum of the squares of n independent
standardized normal random variables has a
2
distribution with n degrees of
freedom; that is, if U
1
,U
2
,..., and U
n
are independent and distributed as
N(0, 1), the sum
has a
2
distribution with n degrees of freedom. One can verify this statement
by determining the characteristic function of each U
2
j
(see Example 5.7, page
132) and using the method of characteristic functions as discussed in Section 4.5
for sums of independent random variables.
Because of this relationship, the
2
distribution is one of our main tools in
the area of statistical inference and hypothesis testing. These applications are
detailed in Chapter 10.
0
2 4 6 8 10 12
0.0
0.2
0.4
0.6
0.8
f
X
(
x
)
n
= 1
n
= 2
n
= 4
n
= 6
x
Figure 7.12 The
2
distribution for n 1, n 2, n 4, and n 6
220 Fundamentals of Probability and Statistics for Engineers
X U
2
1
U
2
2
U
2
n
7:68
TLFeBOOK

The pdf f
X
(x) in Equation (7.67) is plotted in Figure 7.12 for several values
of n. It is shown that, as n increases, the shape of f
X
(x) becomes more
symmetric. In view of Equation (7.68), since X can be expressed as a sum of
identically distributed random variables, we expect that the
2
distribution
approaches a normal distribution as n on the basis of the central limit
theorem.
The mean and variance of random variable X having a
2
distribution are
easily obtained from Equation (7.57) as
7.5 BETA AND RELATED DISTRIBUTIONS
Whereas the lognormal and gamma distributions provide a diversity of one-
sided probability distributions, the beta distribution is rich in providing varied
probability distributions over a finite interval. The beta distribution is char-
acterized by the density function
where parameters and take only positive values. The coefficient of f
X
(x),
can be represented by where
is known as the beta function, hence the name for the distribution given by
Equation (7.70).
The parameters and are both shape parameters; different combinations
of their values permit the density function to take on a wide variety of shapes.
When the distribution is unimodal, with its peak at
It becomes U-shaped when it is J-shaped when
and and it takes the shape of an inverted J when and
Finally, as a special case, the uniform distribution over interval (0,1) results
when 1. Some of these possible shapes are displayed in Figures 7.13(a)
and 7.13(b).
Some Important Continuous Distributions 221
!1
m
X
n;
2
X
2n: 7:69
f
X
x
x
1
1 x
1
; for 0 x 1;
0; elsewhere;
8
>
<
>
:
7:70
( )=()();
1/[B(, )],
B;
;7:71
, >1, x ( 1)/
( 2). , <1; 1
<1; <1 1.
TLFeBOOK
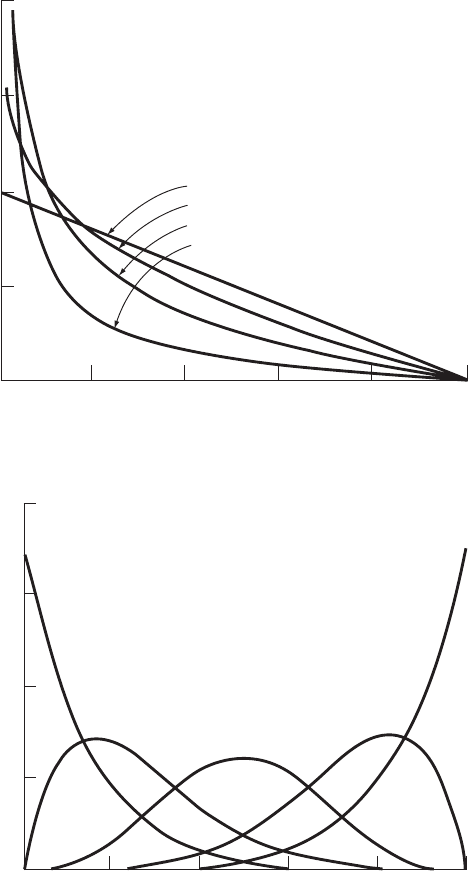
= 1.0
= 0.8
= 0.5
= 0.2
0.0
0.0
1.0
2.0
3.0
4.0
0.2 0.4 0.6 0.8 1.0
x
f
X
(
x
)
(a)
0.0 0.2 0.4 0.6 0.8 1.0
0.0
2.0
4.0
6.0
8.0
f
X
(
x
)
= 1
= 7
= 2
= 6
= 6
= 2
x
= 7
= 1
= 4
= 4
(b)
Figure 7.13 Beta distribution with: (a) and
and (b) combinations of values of such that 8
222 Fundamentals of Probability and Statistics for Engineers
α
α
α
α
α
β
α
β
α
β
α
β
α
β
2and 1:0, 0:8, 0:5,
0:2;
and (, 1,2, ...,7)
TLFeBOOK
The mean and variance of a beta-distributed random variable X are, follow-
ing straightforward integrations,
Because of its versatility as a distribution over a finite interval, the beta
distribution is used to represent a large number of physical quantities for which
values are restricted to an identifiable interval. Some of the areas of application
are tolerance limits, quality control, and reliability.
An interesting situation in which the beta distribution arises is as follows.
Suppose a random phenomenon Y can be observed independently n times and,
after these n independent observations are ranked in order of increasing mag-
nitude, let y
r
and be the values of the rth smallest and sth largest
observations, respectively. If random variable X is used to denote the propor-
tion of the original Y taking values between y
r
and it can be shown that
X follows a beta distribution with 1, and that is.
This result can be found in Wilks (1942). We will not prove this result but we
will use it in the next section, in Example 7.8.
7.5.1 PROBABILITY TABULATIONS
The probability distribution function associated with the beta distribution is
which can be integrated directly. It also has the form of an incomplete beta
function for which values for given values of and can be found from
mathematical tables. The incomplete beta function is usually denoted by
Some Important Continuous Distributions 223
m
X
;
2
X
2
1
:
9
>
>
=
>
>
;
7:72
y
ns1
y
ns1
,
n r s
r s;
f
X
x
n 1
n r s 1r s
x
nrs
1 x
rs1
; for 0 x 1;
0; elsewhere:
8
>
<
>
:
7:73
F
X
x
0; for x < 0;
Z
x
0
u
1
1 u
1
du; for 0 x 1;
1; for x > 1;
8
>
>
>
>
<
>
>
>
>
:
7:74
TLFeBOOK
