Спивак Д.Л. (отв. ред.) Фундаментальные проблемы культурологии : В 4 т. Том III: Культурная динамика

Подождите немного. Документ загружается.

В. Р. Пиотровская, К. Р. Пиотровская, Р. Г. Пиотровский, Ю. В. Романов180

3. На следующем шаге пригодность модели проверяется исходя из того, насколько хорошо

она объясняет и предсказывает вновь открытые объекты

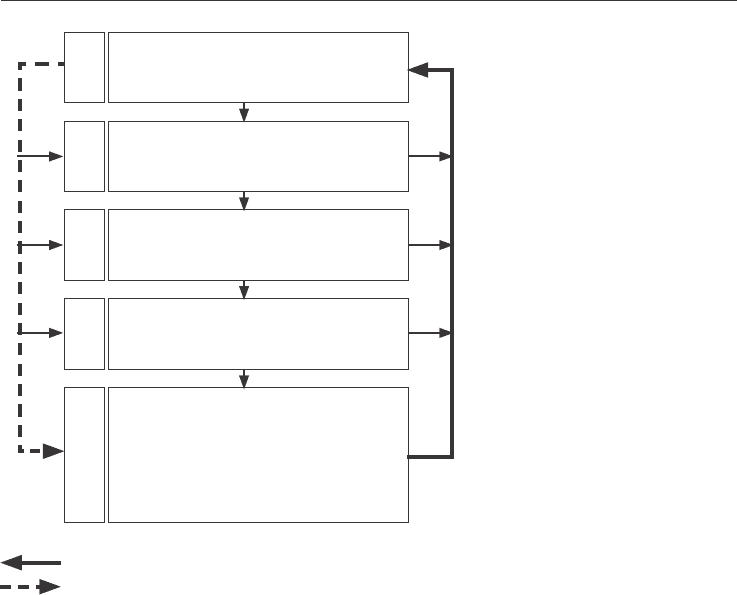
и явления внешнего мира через обратную связь между моделью и оригиналом (рис. 2,

стрелки , ). Такая проверка называется эмпирической.

Эта проверка характеризуется большим разнообразием конкретных ситуаций и доказа-

тельных приемов. К каждому из них должен быть применен критерий истинности (КИ). Наи-

более эффективной с точки зрения КИ является такая счастливая ситуация, когда гипоте-

за подтверждается появлением новых неоспоримых фактов. Лингвистическим примером

такой апробации явилось подтверждение гипотетической схемы индоевропейского корня,

предложенной Ф. де Соссюром (1977, с. 423–425) еще в 70-х гг. XIX в., данными хеттских текс-

тов, открытых, а затем и расшифрованных во втором и третьем десятилетиях ХХ в.

К сожалению, описанный случай апробации лингвистической гипотезы целиком зави-

сит от благоприятного стечения обстоятельств. Хеттские тексты могли обнаружиться на сто

лет позже, когда гипотеза Соссюра была бы уже забыта, они могли остаться не найденны-

ми вовсе. Поэтому современная парадигма языкознания требует выработки приемов, обес-

печивающих опе-ративное получение КИ для той или иной гипотезы. Сильным ходом на

пути создания таких приемов является компьютерное моделирование речевых процессов,

Натурный лингвистический объект

(оригинал или прототип)

Вербальная гипотеза

Теоретический аналог натурного объекта

(модель на искусственном языке)

Эксперимент

Воспроизведение модели через изучение

речевой деятельности испытуемых

с помощью других лингвистических

экспериментов, либо при помощи

лингвистического автомата

Проверка состоятельности и

онтологической пригодности

модели путем доказательно-

экспериментального выявления

и оценки близости порождаемых

ею лингвистических объектов с

объектами естественного языка

и речи

Рис. 2. Схема построения и функционирования лингвистических моделей

— сравнение модели с оригиналом.

— коррекция гипотезы и модели по результатам обратной связи

Культурология: от бесед за чашкой кофе к доказательно-экспериментальной парадигме 181

осуществляемое в лингвистических автоматах. Создаваемые этим путем блоки, входящие в

архитектуру описываемой схемы, называют воспро-изводящими лингвистическими моде-

лями (ВИЛМ), см. рис. 2, блок 5.

Примером одного из наиболее успешных филологических экспериментов, использо-

вавших ВИЛМ, является опыт по определении авторства «Тихого Дона», осуществленного

М. А. Марусенко (1990; 2001) и его помощниками в 80–90-х гг. прошлого века. Опуская дета-

ли матрично-статистической и компьютерной технологий, подробно описанных М. А. Мару-

сенко (1990: 33–157), напомним основные шаги атрибуции шолоховского текста.

На первом шаге, соответствующем 2-му блоку стандартной исследовательской модели,

изображенной на рис. 2, формулируется нулевая гипотеза (H

), согласно которой автором

романа «Тихий Дон» является М. Шолохов. Одновременно выдвигаются три альтернатив-

ных гипотезы, согласно которым претендентами на авторство указанного текста являются:

Ф. Крюков (H

), А. Серафимович (H

), С. Голоушев (Глагол) (H

На втором шаге, путем матрично-статистического анализа из 56 стилеразличающих па-

раметров, разработанных авторами, выделяется пять независимых друг от друга парамет-

ров, обладающих наибольшей различительной силой относительно текстов указанных пре-

тендентов. Такими параметрами являются: 1) число служебных слов, 2) число местоимений,

3) число подчинительных союзов, 4) число слов в аккузативе, 5) число подчиненных предложе-

ний без спрягаемой формы глагола.

На третьем шаге были применены детерминистская, а затем вероятностная процедуры

распознавания (рис. 2, блоки 3 и 4). Идея первой заключалась в том, чтобы определить, су-

щественны или не существенны относительно t-критерия Стьюдента различия в статисти-

ческих характеристиках указанных параметров для попарного сравнения текста «Тихого

Дона» с текстами, наверняка принадлежащими претендентам. Ввиду их трудоемкости ука-

занные процедуры были реализованы в блоке 5 с помощь компьютера.

К сожалению эта часть эксперимента дала надежную атрибуцию только для примерно

13 % текста «Тихого Дона». При этом были получены следующие надежные результаты

относительно отдельных авторов: на первое место по объему атрибуированного текста

вышел А. С. Серафимович (5,9 %), на второе — М. А. Шолохов (2,4 %), остальные претен-

денты показали еще меньшую долю атрибуированного текста. Вместе с тем выяснилось,

что около 64 % текста несут отпечаток авторской манеры как Шолохова, так и Серафимо-

вича.

В связи с этими обстоятельствами исследователям пришлось возвратиться по обратной

связи (рис. 2) к началу всей процедуры с тем, чтобы скорректировать гипотезы и дальней-

шие шаги атрибуции. В ходе этой коррекции был, во-первых, подключен текст «Поднятой це-

лины», а во-вторых, введена еще одна комплексная гипотеза (H

), согласно которой «Тихий

Дон» является результатом совместной работы пары 'основной автор и его соавтор'. Такие па-

ры охватили всех перечисленных претендентов, включая и М. Шолохова.

Последний шаг эксперимента состоял в проверке новой гипотезы с помощью детерминист-

ской, а затем и вероятностной процедур (рис. 2, блок 4). В итоге этой проверки выясняется,

что большая часть текста романа обнаруживает близость с эталонами авторских пар. Основ-

ным участником этих авторских сообществ оказывается А. С. Серафимович. Практически

В. Р. Пиотровская, К. Р. Пиотровская, Р. Г. Пиотровский, Ю. В. Романов182

его сотрудничество статистически прослеживается в 87 % текста, причем 65 % текста объ-

единяют в себе авторские манеры Шолохова и Серафимовича. Отсюда следует, что наиболее

вероятной является гипотеза H

, согласно которой основным автором «Тихого Дона» явля-

ется А. Серафимович, который использовал и редактировал некоторые тексты, написанные

М. Шолоховым. Возможно он использовал также небольшое количество текстов Ф. Крюкова

и С. Голоушева (Глагола).

Этот вывод снова был сопоставлен по обратной связи с историко-литературным контекс-

том появления «Тихого Дона» и фактами биографий обоих писателей, описанными в книгах

С. В. Корягина (2006) и З. Бар-Селлы (2005). Это сопоставление не обнаружило противоречий

между результатами описанного выше матрично-статистического анализа и историко-лите-

ратурными, этнографическими и биографическими фактами.

В последние десятилетия филология меняет свою научную парадигму. Она покидает дис-

куссионный клуб эрудитов-импровизаторов и постепенно занимает место в строю серьез-

ных научных дисциплин. Этот процесс становится возможным не столько за счет появления

новых идей и развития собственных исследовательских технологий, сколько благодаря соче-

танию последних с экспериментальной техникой, взятой из «точных» наук. Такой опыт мо-

жет оказаться полезным для культурологов, желающих превратить свое молодое научное на-

правление в полновесную серьезную науку.

литература

Бар-Селла З. Литературный котлован. Проект «Писатель Шолохов» М.: Изд. Российского гос.

гуманитарного университета, 2005

Корягин С. В. А. С. Серафимович — автор «Тихого Дона». Серия «Генеалогия и семейная

история донского казачества». Вып.63. М.: Русаки, 2006

Кун Т. С. Структура научных революций. Пер. с англ. М.: Прогресс, 1977

Марусенко М. А. Атрибуция анонимных и псевдоанонимных литератур ных произведений

методами теории распознавания образов. Л.: Издательство Ленинградского университета,

1990

Марусенко М. А., Бессонов Б. Л., Богданова Л. М., Аникин М. А., Мясоедова Н. Е. В поисках

потерянного автора: Этюды атрибуции/ Под ред. М. А. Марусенко. СПб.:Филологический

факультет СПбГУ, 2001.

Пиотровский Р. Г. Лингвистическая синергетика: исходные положения, первые результаты,

перспективы. СПб: Филологический факультет СПбГУ, 2006

Пиотровский Р. Г. Статистические модели текста и опыт их лингво-синергетического

анализа// Научно-техническая информация. Серия 2. Информационные процессы и

системы. Ежемесячный научно-технический сборник. 2007, № 8

Соссюр Ф. де. Труды по языкознанию. Пер. с франц. М.: Прогресс, 1977

ICD-10. Version 2007, Chapter V, Mental and Behavior Desorders (FOO—F99)

Kaye A.S. & Tosco M. Pidgin and Creole Languages: A Basic Introduction. München: Lincom, 2002

Lehfeldt W., Altmann G. Протекание падения редуцированных в древне-рус-ском языке в свете

закона Пиотровских// Russian Linguistics. Vol. 27, No. 2, 2003

Культурология: от бесед за чашкой кофе к доказательно-экспериментальной парадигме 183

Piotrowska W. and Piotrowska X. Statistical Parameters in Pathological Text// Journal of Quantita-

tive Linguistics. Vol. 11. No. 1–2, 2004: Special Issue: Festschri in honour of Prof. Rajmund G. Pi-

otrowski. Part III

Vossler K. Frankreichs Kultur und Sprache. 2-te Auage. Heidelberg: C. Winter, 1929

V. R. Piotrovskaya, K. R. Piotrovskaya, R. G. Piotrovsky, U. V. Romanov

Cultural Studies: A coee break talk or the science with a experimental check-up paradigm

Experiment, measurement and quantitation, which precede a profund qualitative notion, have of-

ten been regarded as the hallmarks of modern science. ey ill raise some fundamental problems

in the eld of the humanities. ere exi a deep antinomy between modern experimental and quan-

titative inveigations on the one hand, and arbitrary qualitative improvisations, inherent in the hu-

manities, on the other. e developments of philology over the pa forty years examplies this ri-

valry and opens the modelling way around this problem.

Динамика культурных форм

С. В. Чебанов

Санкт-Петербургский государственный политехнический университет

оптимальность и эКстремальность в Культуре и ципфиаДа

Социальный опыт ХХ века и складывание в естествознании и гуманитарных дисципли-

нах диатропики как учения о разнообразии (Чайковский, 1990) позволяют утверждать сле-

дующее.

1. Разнообразие является фундаментальным свойством широкого класса разноприродных

совокупностей («популятивных объектов» по Г. П. Щедровицкому — Щедровицкий, 1976) —

всех живых организмов (биологических и психосоциальных, включая присущие им культур-

ные артефакты) и обширного круга косных образований, сопоставимых с ферми-ансамбля-

ми1 (электронных оболочек атомов, радикалов молекул, лигандов комплексных соединений,

парагенезисов минералов, комплексов горных пород, ярусов свит и т. д.).

Совокупность имеющихся данных, а также история изучения данных совокупностей

показывают, что разнообразие является фундаментальным свойством в том смысле, что

оно должно трактоваться как неотъемлемое свойство всех рассматриваемых объектов и не

требует при этом никакого объяснения существования этого разнообразия (функциональ-

ного, исторического, энергетического, трактовки как результата реализации экстремаль-

ных принципов и т. д.). Более того, подобные «объяснительные принципы», якобы указы-

вающие источник и причину разнообразия, скорее затемняют, чем проясняют ситуацию.2

Особенно зловредным при этом оказался принцип историзма исходящий из того, что

любое имеющееся актуальное многообразие является следом истории, каждый этап ко-

торой может быть представлен специфическим для него характерным типом организа-

ции, в то время как все остальные трактуются как результат исторического наследия.

При этом всерьез принимается происхождение многообразия из единообразия, возник-

новение чего-либо мыслиться как однократное возникновение унифицированной ор-

ганизации и т. д. При этом в качестве основной модели развития рассматривается ди-

вергенция, хотя под давлением фактических данных и приходиться признать наличие

конвергенции или сетчатого развития. Но, даже признав их существование, им придается

1 Ферми-ансамбли — совокупности частиц-фермионов, подчиняющихся статистике Ферми-Дирака.

В ансамбле фермионов нет двух одинаковых частиц (частиц с одинаковым набором квантовых чисел),

любые две частицы ферми-ансамля хотя бы чем-нибудь различаются (различаются хотя бы одним

квантовым числом — ср. принцип Паули: электроны одной орбитали должны различаться спином).

Ферми-ансамбли являются антиподом бозе-кондесатов — образований, возникающих из бозонов,

частиц подчиняющихся статистике Бозе-Эйнштейна. Бозе-кондесат есть обобществленное состояние

всех образующих его частиц, которые неотличимы друг от друга, а поэтому и неразличимы как инди-

виды (нуклоны в атомном ядре). — (Примеч. автора).

2 Сказанное относится и к предельно широким объяснительным принципам таким, как принцип

спонтанного нарушения симметрии. — (Примеч. автора).

Оптимальность и экстремальность в культуре и ципфиада 185

второстепенное значение, что не позволяет поставить под вопрос значимость диверген-

тного пути развития.3

2. Для совокупностей указанного типа требует объяснения не факт наличия разнообра-

зия, а факт его отсутствия или сужения разнообразия, а также какие-то иные примечатель-

ные его особенности (полимодальность распределения, необычные значения центральные

моментов разных порядков и т. д.). Так, например, кристаллы гипса дают 179 основных типов,

а галита почти всегда куб, что объясняется особенностями их кристаллической решетки.

Возможна и другая ситуация, когда можно говорить о влиянии установок человека на ха-

рактер организации многообразия. В особенности сильно это проявляется тогда, когда речь

идет об исследовании человека. Более того, таковым может быть влияние не только исследо-

вательских установок, но и принятых житейских максим, которые сами по себе определяют

характер спектра многообразия. Так, в брутальных культурах (в особенности военно-коче-

вого типа) существует очень жесткая оппозиция мужского и женского вариантов социали-

зации. Наличие небольшого числа индивидов с морфологическими аномалиями половых

органов или девиантным половым поведением практически никак не влияет на гендерную

структуру таких обществ. В современном же либеральном обществе возникает большой на-

бора критериев гендерности — генетический, морфологический, физиологический, психоло-

гический, социальный и т. д. В результате возникает полный спектр градаций половой при-

надлежности, заполняющих весь ряд между эталонным мужчиной и эталонной женщиной.

Подобная позиция требует пересмотра основных представлений традиционной филосо-

фии, что является базой, например, для предложения о переходе от унитарной онтологии к

полиморфной гетерологии (Керимов, 1999; ср. полионтологии — Чебанов, 2004).

3. Если с помощью каких-либо внешних целенаправленных воздействий достигается еди-

нообразие совокупностей рассматриваемого типа, а через некоторое время интенсивность

этого воздействия ослабевает, то разнообразие через некоторое время восстанавливается.

Время, которое необходимо для восстановления колеблется от ничтожных долей секунды

(для элементарных частиц) до десятков (для социальных образований и биоценозов), сотен

и тысяч лет (для цивилизаций, геологических тел).

Указанное обстоятельство интересно как для технологов, так и для политиков. Для по-

литиков, в частности, важно то, что благодаря спонтанному восстановлению разнообразия,

всякий тоталитарный режим обречен на гибель, причем гибель тем более быстрою, чем чаще

и глубже в нем будут периоды либерализма. При этом, однако, такое восстановление разно-

образия не будет очень быстрым, а потребует двух-трех поколений. При современных темпах

развития государств это означает, что государства прошедшие через стадию тоталитаризма

без иностранной помощи с неизбежностью оказываются на периферии истории.

3 Помимо чисто познавательных затруднений, такая установка формирует особую когнитивную оп-

тику для рассмотрения социальных процессов, причем такую, которая толкает к насильственному

социальному действию. Таковы представления о закономерной смене общественно-экономических

формаций с квалификацией одних из них как реакционных, а других как прогрессивных, трактовка

многоукладности как результата накопления пережитков прошлого, тезис об отставании производс-

твенных отношений от развития производительных сил и т. д. — (Примеч. автора).

С. В. Чебанов 186

4. Совокупности указанного типа, существующие в достаточно гармоничных ситуациях

(не на грани исчезновения, т. е. в ситуациях неэкстремальных в гуманитарно-идеографи-

ческом понимании), характеризуются как еще одним фундаментальным свойством не толь-

ко разнообразием, но и резкой разночисленностью представительства их разных вариантов

в конкретных ансамблях.

Так, в каждом кристалле или каждой пирамиде роста кристалла имеется только одна

(обычно инородная) частица, с которой начинается их рост, и необозримое множество одно-

родных частиц, из которых построен кристалл. Подобным же образом в стае копытных один

вожак, несколько доминантных самцов и множество рядовых особей. Еще более разительно

соотношение численностей в семьях общественных насекомых с одной маткой, нескольки-

ми плодовитыми самцами и множеством рабочих особей. Также построено и государство с

одним верховным правителем, несколькими уникальными позициями высших чиновников,

несколькими десятками министров, сотнями и тысячами крупных руководителей и тысяча-

ми и миллионами рядового населения.

При этом равночисленность представительства или хотя бы сопоставимая численность

разных вариантов является таким же показателем экстремальности в гуманитарном пони-

мании и неблагополучия ситуации, как и отсутствие разнообразия.

Так, незакономерное сопоставимое содержание элементов характерно для магм и термаль-

ных вод, которое сменяется дифференциацией составов при их остывании. Сопоставимые

по численности ассоциации живых организмах возникают на экологически неблагополуч-

ных территориях — на свалках, насыпях железных дорог, на песчаных берегах рек, текущих

в меридиональном направлении, на антропогенных пустырях возникают неустойчивые ас-

социации сорных растений и животных.

Подобным образом и в неустоявшихся человеческих коллективах существует неопреде-

ленно большое число даже формальных лидеров с не вполне легитимным статусом, не гово-

ря о теневых лидерах и множестве претендентов на верховное руководство и высшие руко-

водящие должности.

4. Статистика многообразий указанного типа явно отличается от нормального распреде-

ления, причем конкретный вид распределения, описывающего эти многообразия, является

предметом дискуссий.

Качественно эти распределения характеризуются тем, что для определенного ансамбля,

построенного из элементов данного многообразия справедливы следующие свойства

— большая часть вариантов данного разнообразия различается численностью (частотой),

причем между некоторыми классами эти различия очень велики, в частности

— численность (частота) самого частого и следующего по частоте классов резко различа-

ются;

— имеется большое число малочисленных (низкочастотных) классов, в том числе, большое

число одноэлементных классов.

Разнообразия указанного типа в разных предметных областях описываются распределе-

ниями, известными под разными названиями — Виллиса, Лотки, Мандельброта, Парето,

Ципфа (Арапов, Ефимова, Шрейдер, 1975 а, б; Козачков, 1978; Орлов, 1970, 1976 и мн.др.).

Существует два подхода к описанию этих распределений.

Оптимальность и экстремальность в культуре и ципфиада 187

Первое из них основано на представлении распределения рассматриваемого типа как сме-

си двух распределений (Мартыненко, 1978). При этом распределения высокоактивных ядер-

ных элементов описывается функцией n

= q(k/r — 1)

, в которой k — число классов в распре-

делении, r — ранг класса, n

— численность класса ранга r, а q и γ — некоторые константы,

причем q является некоторым аналог медианы, а γ — характеризует скорость падения чис-

ленности с возрастанием ранга. Распределение же редких периферических элементов описы-

вается функцией n

= q’(lnk/r)

γ'

, в которой k — число классов в этом распределении, r — ранг

класса, n

— численность класса ранга r, а q’ и γ' — некоторые константы, причем q’ являет-

ся своего рода «центром равновесия» экспонентоподобного распределения, а γ' характеризу-

ет скорость падения численности с возрастанием ранга. В результате получается суммарное

распределение близкое в ранговой форме к гиперболическому, но имеющее некоторые отли-

чая в деталях и, по мнению предлагающего его автора, лучше соответствующее эмпиричес-

ким данным. В частности, на границе высоко- и низкочастотых элементов в этом распреде-

лении есть область элементов с частотой более высокой, чем в случае описания материала

гиперболическим распределением («бугорок» на гиперболе). Так или иначе, многообразия

данного типа трактуются в этом случае как смесь двух совокупностей — совокупности не-

большого числа (обычно 15–20) высокочастотных компонентов, из которых в основном пост-

роено «тело» рассматриваемого ансамбля и большого числа редких компонентов, «легирую-

щих» данный ансамбль и выполняющих в нем уникальные функции.

Другой подход основан на представлении ансамблей данного типа как описываемых од-

ним распределением, охватывающим как частые, так и редкие компоненты. Это и будут рас-

пределения, известные как распределения Виллиса, Лотки, Мандельброта, Парето, Ципфа.

Они различаются значение параметров, но в общем имеют следующий вид: n

=Br

-г

(где r —

ранг класса, n

— численность класса ранга r, а B и г — некоторые коэффициенты).

Основные свойства этих распределений были описаны в первой половине ХХ века, но

пристальный интерес к ним появился в 1970-ые годы. Начался он, по-видимому, с работ

Ю. А. Шрейдера, поставившего вопрос о связи этих распределений с общесистемными при-

нципами (Шрейдер, 1967) и Ю. К. Орлова, который, изучая текст «Войны и мира», установил,

что точность соответствия эмпирического распределения данного типа теоретическому не

растет монотонно с увеличением выборки, а зависит от нее более сложным образом (Орлов,

1970, 1976). Детальные исследования показали, что это распределение хорошо выполняет-

ся на отдельных частях романа, написанных на одном дыхании. Это дало основание тракто-

вать факт соответствия эмпирического распределения указанного типа теоретическому как

показатель целостности описываемого им ансамбля. Значительные отклонения от указан-

ного распределения стали интерпретироваться либо как пребывание ансамбля в нестацио-

нарном состоянии, либо отсутствие его целостности — то, что он представляет собой либо

неструктурированный фрагмент одного ансамбля, либо конгломерат фрагментов несколь-

ких ансамблей.

Дальнейшие изучения математических свойств этих распределений и наблюдения над

описываемыми ими ансамблями так или иначе развивали эту интерпретацию Ю. К. Орлова.

Так, В. В. Налимов и Ю. А. Шрейдер стали интерпретировать соответствие распределению

Ципфа как указание на наличие смысла (Налимов, 1978), а М. В. Арапов и Ю. А. Шрейдер как

С. В. Чебанов 188

указание на присутствие сознания (Арапов, Шрейдер, 1977). Появились различные, основан-

ные на этих представлениях, варианты теоретического вывода таких распределений и мно-

жество интерпретирующих и объяснительных их моделей.

В целом, стало общепринятым, что для этих распределений не выполняется центральная

предельная теорема, неопределенны центральные моменты всех порядков, отсутствуют ха-

рактеристические совокупности, а отклонения от этих распределений характерны для не-

целостных образований или ситуаций бифуркаций (см., напр., Шрейдер, Шаров 1982, С. 90

и далее).

Тем не менее, для практических целей при описании таких распределений использовалось

представление разных их зон различными, более привычными распределениями (т.в. прак-

тически использовались те же приемы анализа, что и в подходе Г. Я. Мартыненко). Весьма

примечательным итогом подобных исследований явилось в начале 2000-ых гг. предложение

представителей школы Б. И. Кудрина с целью лучшего согласования с эмпирическими дан-

ными представлять эмпирические распределения данного типа в виде трех каст — высоко-

частотной саранчевой, низкочастотной, ноевой, и промежуточной, как раз соответствующей

бугорку на гиперболе Г. Я. Мартыненко (Философские…, 2002 ).

Так или иначе, сложилась самостоятельная область исследований гиперболических рас-

пределений (получивших название H-распределений), которая ввиду неожиданности полу-

чаемых результатов стала несколько иронически именоваться «ципфиадой» (Борода, Поли-

карпов, 1984; Бычков, 1984; Крылов, 1982; Крылов, Кудрин, 1999, Кудрин, 1996; Трубников,

1996; Тулдава, 1987; Ценологические…, 1996 и мн. др.). Существующее в этой области поло-

жение дел указывает на то, что в изучении распределений указанного типа остается еще мно-

го нерешенных проблем. Однако понятно, что в чистом виде количественная модель Ципфа

не удовлетворительна.

5. Весьма примечательно следующее обстоятельство. Многие модели теоретического вы-

вода распределений данного типа, предложенные после работ Ю. К. Орлова, построены на

использовании экстремального принципа в математическом его понимании (Арапов, Шрей-

дер, 1978; Левич, 1980; Трубников, 1996)4.

М. В. Арапов и Ю. А. Шрейдер целенаправленно задались вопросом о связи таких распре-

делений с экстремальными принципами. В результате ими была предложена следующая мо-

дель.

Очевидно, что в распределениях данного типа речь идет о минимальности симметрии, на

что указывает резкая неравночисленность разных классов. Минимально симметричным та-

ким распределением будет распределение, представленное двумя классами, одному из кото-

рых будут принадлежать все компоненты данного ансамбля, а другой будет пустым. Очевид-

но, что такое распределение неинтересно ввиду его тривиальности (хотя для него и можно

4 Вообще говоря, приверженцем такого подхода был еще сам Дж. Ципф, рассматривавший наличие

предлагаемого распределения как результат проявления принципа наименьшего усилия в процессе

порождения текста (Zipf, 1949) — ср. принцип экономии усилия в речевой деятельности А. Мартине.

Идея оптимальности важна и для Ю. К. Орлова, полагавшего, что подчиняющиеся обсуждаемой зако-

номерности тексты оптимальны для восприятия (Орлов, 1970). — (Примеч. автора).

Оптимальность и экстремальность в культуре и ципфиада 189

ввести формальную меру симметрии). Поэтому предлагается рассмотреть коразбиение —

разбиение, дополнительное к исходному. Каждый класс этого распределения содержит не

более одного элемента из каждого класса исходного распределения и эти классы упорядоче-

ны как это принято для представления распределений в ранговой форме. Симметрия рас-

пределения характеризуется интегральной характеристикой произведения симметрии раз-

биения и коразбиения. Именно это произведение в соответствии с логикой экстремального

принципа и должно быть минимальным.

Если в качестве величины симметрии принять S=n

!…n

!, где n

— численность i-го клас-

са рангового распределения, то A=f•g, где A — интегральная характеристика симметрии рас-

пределения, являющаяся произведением симметрии разбиения f и симметрии коразбиения

g, определяемых по приведенной формуле. Условие минимума A достигается при n

=Bi

-г

(где

B и г — коэффициенты, зависящие от параметров функций f и g — решение уравнение Эйле-

ра из вариационного исчисления; Шрейдер, Шаров, 1982, С. 91–104), что с точностью до коэф-

фициентов соответствует распределению Ципфа.

Вслед за работами Ю. А. Шрейдера было получено еще несколько других выводов распре-

деления данного типа на основании экстремальных принципов (например, как наиболее

экономичный вариант использования ресурса конкурирующими за него потребителями —

Левич, 1980; ср. Трубников, 1996).

Таким образом неэкстремальная в гуманитарно-идеографическом понимании ситуация

(т. е.. близкая к оптимальной в гуманитарно-идеографическом понимании) является экстре-

мальной в прецизионно-номотетическом понимании (минимум произведения симметрий).

Тем самым приводимый результат является примером соотнесения понимание экстремаль-

ности и оптимальности в двух типах дискурса.

6. Содержательно полученные результаты означают следующее.

— Образования обсуждаемого класса, рассматриваемые как целостные, состоят из весьма

разнообразных резко разночисленных компонентов, распределенных принципиально нега-

уссовым образом. В стационарных и квазистационарных условиях такие распределения мо-

гут аппроксимироваться Н-распределениями.

При этом число единичных компонентов (т. е. число классов однокомпонентных классов)

в идеальном Н-распределении равно разности численности первого и второго самых высо-

кочастотных классов.

— Нарушение целостности образований, как и изменение лимитационной структуры при-

водит к видимым отклонения от Н-распределения:

— Ограничение лимитирующего ресурса приводит к увеличению неравночисленности

компонентов и уменьшению их разнообразия.

— Увеличение лимитирующего ресурса ведет к уменьшению неравночисленности и увели-

чению разнообразия.

Имея в виду ценность разнообразия, это означает, что при перестройках сложных обра-

зований, например, социальных (в кризисных ситуациях экстремальных в гуманитарном

понимании) должны приниматься специальные меры по охране разнообразия, причем

разнообразия как такового, его типа и раздельно разнообразия редких и частых компо-

нентов.