Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D

–

157

– [149–162] 13.3.2008 11:19AM

The Anderson criteria are derived from two

basic principles: (i) there are no stresses, normal

or shear, across a free horizontal surface, and (ii)

the largest shear stress occurs across planes

between the directions of maximum and mini-

mum principal stress. The existence of the free

surface requires that one of the principal stress

directions be vertical, normal to the surface. This

applies not just to the surface itself but to all

depths much smaller than the horizontal scale

over which the stresses are averaged, and it is

therefore a constraint on theories of the causes

of geologically observed surface faults. Thus, the

other two principal stresses are horizontal and

there are only three ways in which they can be

oriented. The vertical stress may be the direction

of maximum, 

, intermediate, 

, or minimum

principal stress, 

, and in each case the other

two principal stresses are the horizontal stresses.

As generally applied, the principal stresses are

converted to the rock mechanics convention

with compression positive. With this convention,

the ranking 

>

corresponds to the most

compressive to least compressive stress.

In a region of compression, 

and 

are both

horizontal, with 

vertical, and thrust (reverse)

faulting (Fig 11.7) occurs. Extension, in which

both horizontal stresses are smaller than the

vertical (and are negative at the surface), causes

normal faulting (Fig. 11.7). Strike-slip faulting

(Fig. 11.7) occurs when the maximum and mini-

mum stresses are horizontal.

An unconfined rock will fail when subjected

to shear stress greater than its internal strength,

. The failure usually takes the form of relative

motion across a plane that is oriented in the

direction of maximum shear, i.e. at 458 to the

maximum and minimum principal stresses. At

depth, rocks are more resistant to shear failure

because they are subjected to confining pressure

of the overburden. In addition to overcoming

intrinsic internal strength, shears must be large

enough to overcome frictional effects from the

overburden pressure. The frictional stress is

equal to the product of normal stress, 

, across

a fault plane (with compression taken as posi-

tive) and a friction coefficient. The failure plane

is then not the 45

plane of maximum shear,

because the frictional stress is reduced by

turning the normal to the failure plane towards

the axis of minimum stress. This occurs at an

angle such that the reduction in shear stress is

compensated by a reduction in the normal stress.

Coulomb’s equation describes this process and

gives the condition for failure as

 ¼ 



þ S

; (11:36)

where t is the limiting shear stress at which fail-

ure occurs, 

is the friction coefficient, and S

the internal strength or cohesion. The straight

line in Fig. 11.6(a) gives the failure criterion

(Eq. (11.36)), which lies tangent to the limiting

Mohr circle at the point of failure. The rock is

stable for stress fields having circles that lie

below the failure line. As Fig. 11.6(c) illustrates,

increasing pressure stabilizes against failure

because larger shears are required to generate

Mohr circles that intersect the failure criterion.

From laboratory observations, Byerlee (1978)

found that a value 

¼0.6 to 0.85 applies to many

common rock types. The lower value applies to

wet rock or rock under high confining pressure

and the upper value to dry rock at low confining

pressure. Equation (11.36), known as Byerlee’s

law, is the equation of a straight line (a better

approximation is a convex curve) that is plotted

on the Mohr diagram to describe conditions for

failure. At the point of failure, 2 of Eq. (11.30) is

an obtuse angle. Therefore, the angle, ,between

the normal to the plane of failure and maximum

principal stress direction is greater than 458.The

slope of the failure line is tan ,where is

referred to as the angle of internal friction, so that



¼ tan : (11:37)

Then from Fig. 11.6(a),

2 ¼

þ : (11:38)

In structural geology one is interested in , the

angle between the dip of the fault plane and 

which is the complement of . Then

 ¼

  ¼

tan

1

ð1=

Þ: (11:39)

For 

¼0.85,  ¼24.88. In general, failure planes

are predicted to occur at small angles to the

directions of maximum principal stress.

11.5 CRUSTAL STRESS AND FAULTING 157

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D

–

158

– [149–162] 13.3.2008 11:19AM

The Coulomb criterion applies to dry materi-

als. For rock subjected to internal pore pressures,

the outward pressure of the fluid reduces the

effective normal stress on the solid matrix, and

the rock fails at lower shear stress. The Mohr

circles in Fig. 11.6(c) move to the left, corres-

ponding to a reduction in normal stress. We

replace normal stress in Eq. (11.36) with an effec-

tive normal stress 



given by the externally

applied normal stress, 

, minus the internal

stresses that are generated by pressurized fluids

in the rock. The internal pore fluid pressure gen-

erates an outward directed stress, P

, propor-

tional to the pressure in the fluid and the area

fraction of the fault plane occupied by pore

space. In many sedimentary rocks, pore fluids

are pervasive in wet grain–grain boundaries

and P

is nearly equal to the pore pressure. In

more compact rock, with restricted fluid filled

pores, P

is generally smaller, although, in some

cases, sealed pores may have high internal pres-

sures. Equation 11.36 becomes

 ¼ 

ð

 P

ÞþS

; (11:40)

written as

 ¼ 



ð1  l

ÞþS

(11:41)

 ¼ 





þ S

;

where l

, known as the Hubbert–Rubey coeffi-

cient, is the ratio of pressure from pore fluids to

normal stress, and 



is the effective normal

stress. Then



: (11:42)

Alternatively,

 ¼ 





þ S

; (11:43)

where 



¼ 

ð1  l

Þ is the effective friction

(Section 13.7).

We return to the Anderson criteria, which

describe maximum stress directions for the differ-

ent fault mechanisms. In a compressional regime

where the maximum principal stress is horizon-

tal, the dips of fault planes, relative to the surface,

are expected to be shallow. In a normal faulting

regime where the maximum stress is vertical, the

dips of fault planes are expected to be steep. In a

strike-slip regime faults should be vertical and

angled closer to the direction of maximum prin-

cipal stress than to the direction of minimum

principal stress. However, geological and seismo-

logical observations of faults indicate that their

orientations can be explained by these equations

with a value of 

much smaller than suggested by

laboratory measurements (0.6 to 0.85), as in

Table 11.2. These criteria refer to mechanically

isotropic material, but in many cases established

faults are planes of weakness that control fault

movements. Then the Anderson criteria refer to

the direction of stresses that caused the faults in

the first place and not necessarily to the present

stress.

Sibson and Xie (1998) plotted a histogram of

the dip angles of 31 reverse faults for which

there are seismic or field estimates of the geom-

etry of the fault planes (Fig. 11.8(a)). The mean of

their broad distribution is 398. Jackson and

White (1989) present a histogram of dips for 15

normal fault events with a mean value of 50.38

(Fig. 11.8(b)). The modest number of events in

each case invites doubt about the statistical sig-

nificance of the small average deflections from

458, but they are clearly incompatible with fric-

tion coefficients as high as the laboratory values

of 0.6 to 0.85. While we know that established

fault planes have powdered, soft material (gouge),

compatible with a low friction coefficient, this

Table 11.2 Average fault dips for different

friction coefficients compared with

observations by Sibson and Xie (1998) and

Jackson and White (1989)

Dip

(

¼0.85)

Dip

(

¼0.2) Observations

Normal

fault

65.28 50.7 8 50.38

Strike-

slip

fault

vertical,

24.88

to 

vertical,

39.38 to



–

Reverse

fault

24.88 39.3 8 398

158 DEFORMATION OF THE CRUST: ROCK MECHANICS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D

–

159

– [149–162] 13.3.2008 11:19AM

does not explain how the faults formed in the

first place and that is what matters in consider-

ation of the angles. Evidently pore pressure in

faults has a more significant effect that is yet

to be satisfactorily explained. It is especially

obvious that the conventional concept of friction

can apply to only very shallow faults and needs

modification to apply to earthquakes at even

modest depths, where overburden pressure

ensures very high normal stresses across faults.

11.6 Crustal stress: measurement

and analysis

A basic starting point in generating a theoretical

model of stresses is to find solutions that satisfy

the equations of motion. The equations of

motion in a continuous medium are found by

applying Newton’s third law to elementary vol-

umes subjected to a stress field 

. Consider a

parallelepiped of length x and cross-sectional

area y z (Fig. 11.9). The normal force acting on

the face ABCD is

¼ 

yz; (11:44)

and on face A

¼ 

@

x



yz: (11:45)

The net force from this stress component is:

F ¼ F

 F

@

xyz: (11:46)

If we consider the shear stresses on the other two

sides in a similar fashion we obtain additional

forces in the x-direction of

@

xyz;

@

xyz:

Summing these forces, the net force per unit

volume in the x-direction due to the stress

imposed on the parallelepiped by the material

exterior to it is

force

volume

@

: (11:47)

0 1020304050607080

Reverse Faults

Dip Angle (degrees)

Number

31 events

0 102030405060708090

Dip Angle (degrees)

Normal Faults

Number

with surface faulting

15 events

FIGURE 11.8 Histograms of measured dip angles of

faults, as tests of the Anderson criteria (Table 11.2).

(a) Reverse faults (mean dip angle 398), after Sibson

and Xie (1998). (b) Normal faults (mean dip angle 50.38),

after Jackson and White (1989).

A' B'

FIGURE 11.9 Geometry of an elementary volume in a

stressed medium.

11.6 CRUSTAL STRESS: MEASUREMENT AND ANALYSIS 159

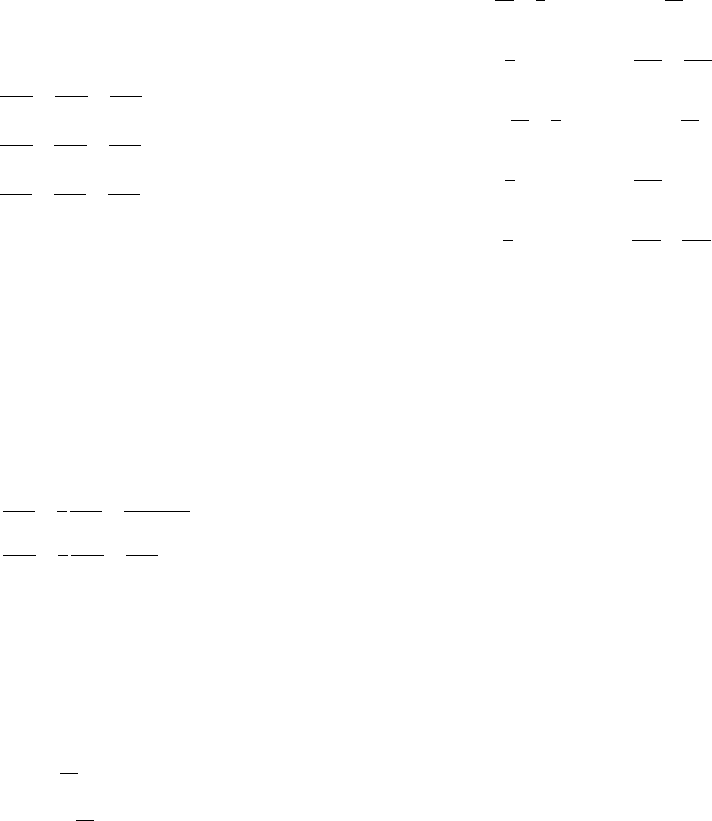
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D

–

160

– [149–162] 13.3.2008 11:19AM

In addition to these external forces, the vol-

ume may be subjected to an internal body force,

most importantly gravity, mg, which must

be added to the above equation. Let X be the

component of the body force per unit mass

(g in the gravity case). Then the force per unit

volume is X. The equation of motion becomes

force=volume ¼ density  acceleration. For three

dimensions

@

þ X ¼ 

;

@

þ Y ¼ 

;

@

þ Z ¼ 

: (11:48)

Solutions to these differential equations are

used in numerous applications from seismo-

logy to structural geology. In this section we

consider the equilibrium versions with no

acceleration.

The equations of motion (11.48) may also be

expressed in cylindrical or spherical coordinates

(Jaeger and Cook, 1984). The equilibrium equa-

tions for horizontal plane stress in cylindrical

coordinates are

@

r

@



 



¼ 0;

@

r

@



@

2

r

¼ 0;

(11:49)

where the body forces are omitted because we

are considering (r,) geometry in the horizontal

plane perpendicular to the gravitational force.

Consider a cylindrical hole of radius R in an

elastic medium subjected to a pressure P. The

solution that satisfies Eq. (11.49) is



¼P

;





¼P

;



r

¼0; for r

(11:50)

This solution describes stresses around pressur-

ized conduits such as a magma conduit or a pres-

surized borehole.

A related solution, and one of the most impor-

tant in rock mechanics, gives the stresses outside

a pressurized cylindrical hole with specified

principal stresses {

, 

} at infinity (Jaeger and

Cook, 1984). It is the theoretical basis for

interpreting stress measurements in the Earth

using hydrofracture, overcoring and borehole

breakouts.



¼P

ð

þ 

Þ 1 



ð

 

Þ 1 



cosð2Þ;





¼P

ð

þ 

Þ 1 þ





ð

 

Þ 1 þ



cosð2Þ;



r

¼

ð

 

Þ 1 þ





sinð2Þ;

(11:51)

where  is measured from the direction of 

Hydrofracture is the process whereby water

pressure in a conduit, such as a borehole,

becomes large enough to fracture the surround-

ing rock, forming a crack into which the water

flows. Hydrofracture occurs in natural systems

such as in geothermal regions. The equivalent

process, magma-fracture, occurs in volcanic

areas where magma fractures rock to generate

dikes and sills. Hydrofracture is used in the oil

industry to fracture oil reservoirs, and to

increase permeability for secondary recovery of

reserves. The hydrofracture process involves

sealing off a segment of the borehole with pack-

ers, and pumping liquid into the sealed section

until the surrounding rock breaks. The pressure

is monitored throughout, and various methods

are used to estimate the directions and orienta-

tions of fractures. In addition to its oil reservoir

use, the method is one of the most important in

determining the regional stress field, because

fractures open in the direction of minimum prin-

cipal stress, and fluid flow into the cracks is

governed by their dimensions.

In order to initiate a vertical fracture, for

example, the tangential stress, 



, at the bore-

hole, r ¼R in Eq. (11.51), must be equal to the

tensional strength of the rock, T





¼T

160 DEFORMATION OF THE CRUST: ROCK MECHANICS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D

–

161

– [149–162] 13.3.2008 11:19AM

From Eq. (11.51) we obtain at r ¼R,





¼P þð

þ 

Þ2ð

 

Þcosð2Þ:

The tangential stress becomes most tensile (nega-

tive) at  ¼0. Then

¼ P þ 

 3

; (11:52)

i.e. a crack forms at P

¼T

þ3



(Fig. 11.10)

and water flows from the borehole into the

crack. Before the crack becomes very large and

influences the regional stresses by its presence,

the pressure is reduced, flow ceases, and then

the pressure is applied once more. This time the

internal pressure inflates an already broken

crack of no tensile strength and we obtain the

simpler equation

¼ 3

 

: (11:53)

is the breakdown pressure, which is measured

at the well-head. Flow resumes at P ¼P

(Fig 11.10).

We thus have one equation, Eq. (11.53), in two

unknowns, 

and 

,andrequireafurther

measurement. The crack is allowed to grow. If

the material is impermeable and isotropic, the

usualassumption,thecrackwillopennormalto



andextendinthedirectionof

.Afterthe

crack has been fully inflated, the pressure at the

well-head is reduced, and the crack collapses,

reducing the flow to zero. For a large crack 

has no influence on the flow, and the internal

pressure is dependent on P 

.Thecrackcloses

when P 

¼0. Thus the shutin or closure pres-

sure, P

, measured just before closure, gives an

estimate of 

. In many situations the third prin-

cipal stress can be taken as 

¼gz. Then the

hydrofracture measurement can, in principle,

determine all the components of the stress field.

The direction the crack travels is measured by

in-borehole methods involving televiewers, imp-

ression packers, or externally by detecting the

deformation field at the surface by arrays of very

sensitive tiltmeters (Davis, 1983).

Another method of estimating stresses,

known as overcoring, involves drilling out the

rock in a cylindrical annulus around a borehole,

effectively isolating it from the tractions of the

surroundings. Calipers are used to measure the

change in shape as a function of depth after

overcoring. The associated strains may be con-

verted to stresses if the elastic constants have

been determined so that Eq. (11.51) can be

applied to determine 

and 

Also, Eq. (11.51) is applied to the analysis of

borehole breakouts. These are localized failure of

the borehole walls in which rock spalls off along

sections of the circumference closest to the axis of

minimum principal stress 

.Asqueezedhole

breaks along its sides. Equation (11.51) with

P ¼0 describes the stress concentration that

occurs when a hole is drilled into a region of

principal stresses 

, v

, 

. The greatest com-

pression in the rock occurs for  ¼908,which

for r ¼R gives 



¼3



. The compressive

stress causes cracks that are parallel to the cir-

cumference and flakes of rock spall from each

side leaving the bore elongated in the horizontal

plane. The direction of minimum principal stress

is mapped by inserting a caliper and measuring

the orientation of the elongation. While useful in

giving stress directions, this method gives no

information on the magnitudes of the stresses.

Time

Pressure

Flow

Pressure

Flow

Hydrofracture

FIGURE 11.10 Pressure at the well-head for a

hydrofracture experiment. Pressure in the borehole is

increased to P

until the rock fractures, fluid flows into

the crack and the pressure decreases. When the flow

stops the crack closes and pressure increases again to

, which is the breakout pressure at which the crack

re-opens to flow. P

is the shutin or crack closure

pressure when flow stops.

11.6 CRUSTAL STRESS: MEASUREMENT AND ANALYSIS 161

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D

–

162

– [149–162] 13.3.2008 11:19AM

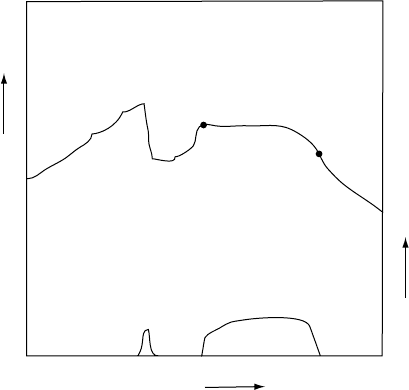
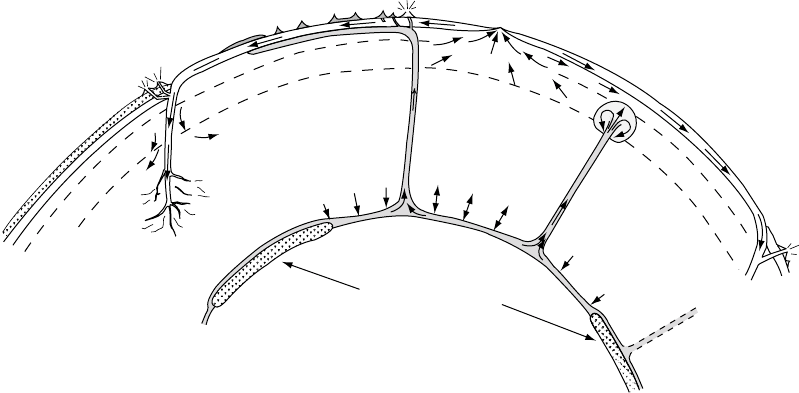
Figure 11.11 is a plot of stress regimes from

the world stress map (Reinecker et al, 2004),

which combines hydrofracture, overcoring and

borehole breakout measurements with earth-

quake focal mechanisms (Chapter 14) and geo-

logical indicators such as faulting type. Large

regions of the world exhibit coherent stress

directions. Diverging and converging arrows

represent regions of tension or compression,

respectively. Adjacent oppositely directed arrows

indicate strike-slip regions. For example, the

Aleutian subduction zone is a thrust regime,

whereas the San Andreas fault is strike-slip,

but further inland, the Basin and Range prov-

ince of west North America is a normal faulting

regime, as is Baja California, where crustal

extension is taking place. The major active con-

tinental rift zones of the world, which include

the East African rift in Kenya, the Rio Grande

rift in New Mexico, and Lake Baikal, Siberia, are

all in regions of extensional stress. The spatial

coherence of stress can be explained by a com-

bination of large-scale stresses from plate tec-

tonics and buoyancy stresses associated with

uplift, as considered further in Sections 13.4

and 13.6.

180° 210° 240° 270° 300° 330° 0° 30° 60° 90° 120° 150° 180°

–60°

–6°

–30°

–3°

0° 0°

30°

60°

FIGURE 11.11 Selected details from the world stress map by Reinecker et al. (2004). Diverging arrows represent

regions of extension and converging arrows indicate compression. Anti-parallel pairs of arrows denote strike-slip

faulting.

162 DEFORMATION OF THE CRUST: ROCK MECHANICS

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C12.3D

–

163

– [163–180] 13.3.2008 11:21AM

Tectonics

12.1 Preamble

Seismicity (seismic activity) is a word coined by

Gutenberg and Richter (1941) to encompass

earthquake occurrences, their mechanisms,

magnitudes and especially their geographical

distribution. Although we have known for more

than 150 years that earthquakes are concentrated

in extended, but relatively narrow bands across

the Earth (Fig. 12.1), the pattern remained more

or less mysterious until it became a cornerstone

of the theory of plate tectonics in the 1950s and

1960s. According to this theory the surface of

the Earth is divided into almost rigid plates that

are in relative motion, with earthquakes occur-

ring mainly at the boundaries. Especially signifi-

cant in this connection are the deep focus

earthquakes, which mark the subduction zones

where cooled surface material plunges into the

mantle. They provide direct evidence of the deep,

convective motion that drives the plates.

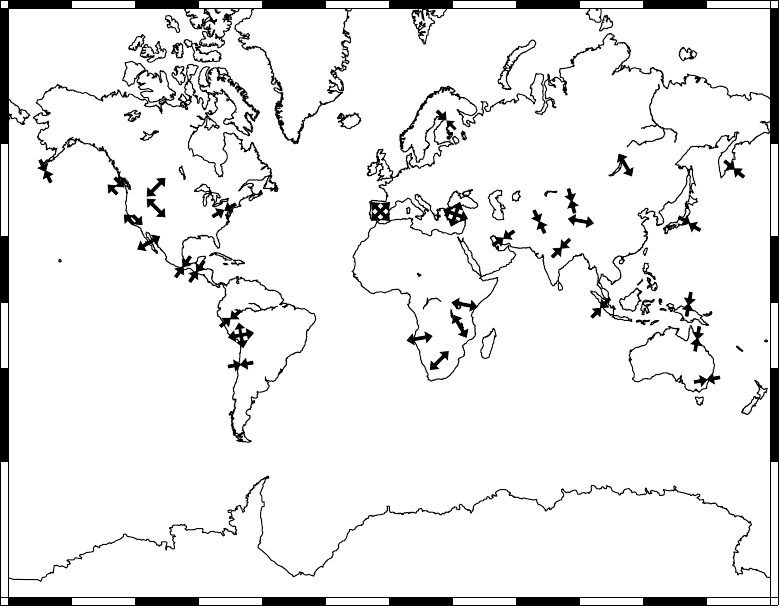
Therearenowmorethan3000globallydistri-

buted seismological stations routinely contributing

data to the International Seismological Centre at

Thatcham, UK. Although they are unevenly dis-

tributed, they suffice to locate reliably all earth-

quakes of magnitude 5 or greater (the definition of

magnitude and its relationship to energy are dis-

cussed in Section 14.6). By restricting attention to

these events we can view the pattern of world

seismicity without a bias towards instrumented

areas. Earthquake epicentres (Fig. 12.1), that is

the surface points directly above the foci (hypo-

centres) where earthquakes actually occur, outline

the plates, which are identified in Fig. 12.2. Intra-

plate earthquakes also occur, although much less

frequently, demonstrating that the plates are

not completely rigid. However, plate deformation

is slight enough to neglect in calculations of their

relative motions. The pattern of mantle convec-

tion suggested by the distribution of earthquakes

in Fig. 12.1 is confirmed by studies of the first

motions of seismic waves (Section 14.4), which

are used to infer the relative motions of the plates

at their common boundaries.

The development of our understanding of

global scale tectonics was pioneered by paleo-

magnetism, which established the credibility of

continental drift (Section 25.6). Subsequently,

laser ranging to satellites (SLR), very long baseline

interferometry (VLBI), and, now much more

extensively, the global positioning system of sat-

ellites (GPS) have been used to show that the geo-

logically inferred relative motions of continental

blocks are on-going. Another crucial contribution

by paleomagnetism was the establishment of the

sequence of geomagnetic reversals (Section 25.4).

Fresh igneous crust produced at the spreading

ocean ridges is magnetized during or shortly

after its appearance and carries a record of the

field with it as it moves away from the ridges. This

has produced a series of linear ocean floor

magnetic anomalies parallel to the ridges, corre-

lated with the irregular alternations of the pol-

arity of the geomagnetic field seen in the

magnetism of continental rocks. For the last few

million years the reversals have been dated iso-

topically with sufficient accuracy to determine

the rates of ocean floor spreading from the

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C12.3D

–

164

– [163–180] 13.3.2008 11:21AM

FIGURE 12.1 Epicentres of earthquakes with magnitudes exceeding 5.0 that occurred in 1980–1990. National Earthquake Information

Center, US Geological Survey, Denver, courtesy of Susan K. Goter.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C12.3D

–

165

– [163–180] 13.3.2008 11:21AM

0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160170180190200210220 230 240 250 260 270 280 290 300 310 320330340350360

–90

–80

–70

–60

–50

–40

–30

–20

–10

LONGITUDE (degrees)

LATITUDE (degrees)

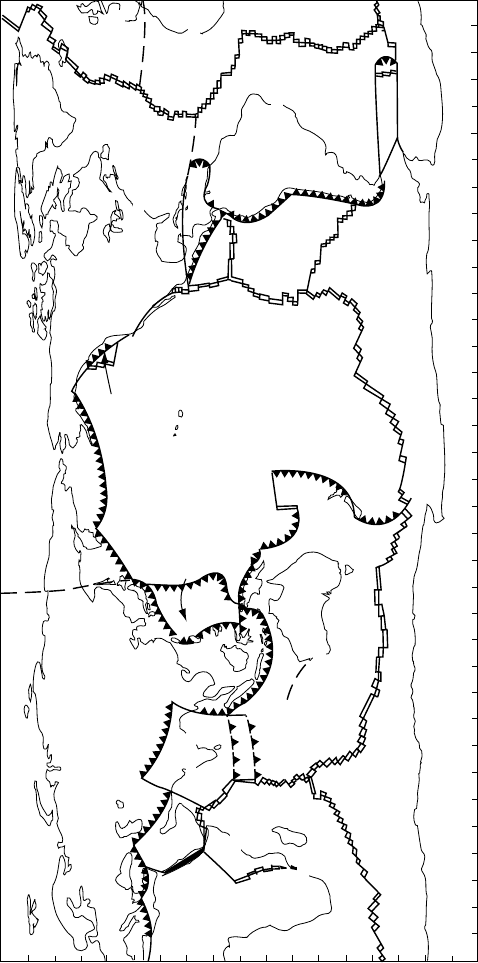
PACIFIC

N. AMERICA

CARIB.

S AMERICA

EURASIA

AFRICA

SCOTIA

PHILIPPINE SEA

AUSTRALIA

INDIA

EURASIA

JUAN DE FUCA

COCOS

NAZCA

ANTARCTIC

NUBIA

SOMALIA

AFRICA

ARABIA

FIGURE 12.2 The Earth’s major plates. Subduction zones are represented by ‘shark’s teeth’ drawn on the over-riding plates and showing

the motion of the subducting plates beneath. Spreading centres are marked by double lines, but they are fragmented by transform faults

(single lines, as in Fig. 12.7). Broken lines mark uncertain boundaries.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C12.3D

–

166

– [163–180] 13.3.2008 11:21AM

spacing of the magnetic stripes. For the period

back to 100 million years or so the magnetic

polarity time scale is established by the sea floor

anomalies, with the assumption that the spread-

ing rate is constant.

A third paleomagnetic observation with fund-

amental implications for tectonics is the motion

of the plates across volcanic ‘hot spots’ that are

anchored deep in the mantle. The idea of a man-

tle reference frame originated with observations

made in Hawaii. The presently active volcanos

are on Hawaii Island at the south-east end of

the island chain, latitude 198, an d at Lo ihi, a

submarine volcano immediately t o the SE of

that. The other islands in the chai n follow a

line in the north-west direction and have ages

that increase linearly with distance in that direc-

tion. Paleomagnetic measurements showed that

they were all formed at latitude 198, that is, at the

latitude of the present centre of volcanism. The

Pacific plate is moving across a more or less sta-

tionary mantle hot spot that produces a series of

volcanos, with their extinct and eroding edifices

steadily drifting north-west.

The concept of deep mantle convective plu-

mes, with local hot spots, such as Hawaii, as their

surface expressions, originated with Morgan

(1971) and has become an important component

of our understanding of mantle convection, as

illustrated in Fig. 12.3. It is not certain how many

there are because they are not all equally active.

The four most active occur in quite different sit-

uations. Hawaii and Reunion are oceanic islands,

Iceland sits astride the mid-Atlantic ridge and a

mid-continent hot spot occurs in Zaire, central

Africa. Yellowstone is a commonly cited example,

but appears to be physically different from the

others and may have a somewhat different cause.

Surface traces of several hot spots are recognized,

including some others on the Pacific plate in lines

roughly parallel to the Hawaiian chain. Those on

other plates have independent traces oriented

according to their plate motions. The apparent

fixity of the Hawaii hot spot invited the supposi-

tion that they are all more or less stationary with

respect to an immobile deep mantle and provide a

reference frame for plate tectonics. It is now clear

that they are moving with respect to one another,

but at speeds lower than the plate motions and

that they give an indication of convective motion

deep in the mantle. Particularly relevant is a check

on the relative motion of the two major oceanic

hot spots that are remote from plate boundaries,

Hawaii and Reunion (see Section 12.4).

The discoveries of paleomagnetism made

plate tectonics a convincingly quantitative

Asthenosphere

670 km

CORE

Crypto-continents

Established

plume

New

plume

Mid-ocean ridge

Hot spot

Volcanic chain

Subduction

zone

Island

arc

Andesite volcanos

Contine

Crypto-ocean

Extinct

plume

FIGURE 12.3 A pictorial cross-section of mantle convection.

166 TE C TO N I CS