Stefanica D. A Primer for the Mathematics of Financial Engineering
Подождите немного. Документ загружается.


Financial Engineering Advanced Background Series
Published or forthcoming
1.
A
Primer
for
the
Mathematics
of
Financial
Engineering,
by
Dan
Stefanica
2.
Numerical Linear Algebra
Methods
for Financial Engineering Applica-
tions,
by
Dan
Stefanica
3. A
Probability
Primer
for
Mathematical
Finance,
by.Elena
Kosygina
4. Differential
Equations
with
Numerical
Methods
for Financial Engineering,
by
Dan
Stefanica
A PRIMER
for
the
MATHEMATICS
of
FINANCIAL ENGINEERING
DAN STEFANICA
Baruch College
City University of New York
FE PRESS
New York

FE
PRESS
New York
www.fepress.org
Information
on
this title: www.fepress.org/mathematicaLprimer
©Dan
Stefanica 2008
All
rights reserved. No
part
of
this
publication
may
be
reproduced, stored
in
a retrieval system, or
transmitted,
in
any form or
by
any means, electronic, mechanical,
photocopying, recording,
or
otherwise,
without
the
prior
written
permission
of
the
publisher.
First
published 2008
Printed
in
the
United
States
of America
ISBN-13 978-0-9797576-0-0
ISBN-IO 0-9797576-0-6
To Miriam
and
to
Rianna

Contents
List
of
Tables
Preface
Acknowledgments
How
to
Use
This
Book
O.
Mathematical
preliminaries
0.1
Even
and
odd
functions
0.2 Useful
sums
with
interesting proofs .
0.3 Sequences satisfying linear recursions
0.4
The
"Big
0"
and
"little
0"
notations
0.5 Exercises
........
.
1
Calculus
review.
Options.
1.1 Brief review
of
differentiation
1.2
Brief
review
of
integration
. .
1.3 Differentiating definite integrals
1.4 Limits
........
.
1.5
L'Hopital's
rule
........
.
1.6 Multivariable functions
....
.
1.6.1 Functions
of
two variables
1.
7
Plain
vanilla
European
Call
and
Put
options
1.8
Arbitrage-free
pricing
..........
.
1.9
The
Put-Call
parity
for
European
options
1.10 Forward
and
Futures
contracts.
1.11 References
1.12 Exercises
.........
.
Vll
xi
xiii
xv
xvii
1
1
4
8
12
15
19
19
21
24
26
28
29
32
34
35
37
38
40
41

viii
CONTENTS
2
Numerical
integration.
Interest
Rates.
Bonds.
45
2.1 Double
integrals.
. . . . . . . . .
45
2.2
Improper
integrals
..............
48
2.3 Differentiating improper integrals . . . . . .
51
2.4 Midpoint, Trapezoidal,
and
Simpson's
rules.
52
2.5 Convergence of Numerical
Integration
Methods
56
2.5.1 Implementation of numerical integration
methods
58
2.5.2 A concrete
example.
.
62
2.6
Interest
Rate
Curves . . . . . 64
2.6.1
Constant
interest
rates
66
2.6.2 Forward
Rates.
. . . .
66
2.6.3 Discretely compounded interest 67
2.7 Bonds. Yield, Duration, Convexity . .
69
2.7.1 Zero
Coupon
Bonds.
. . . . . .
72
2.8 Numerical implementation of
bond
mathematics
73
2.9 References 77
2.10 Exercises .
78
3
Probability
concepts.
Black-Scholes
formula.
Greeks
and
Hedging.
81
3.1 Discrete probability
concepts.
. . . . . . . .
81
3.2 Continuous probability
concepts.
. . . . . .
83
3.2.1 Variance, covariance,
and
correlation
85
3.3
The
standard
normal variable 89
3.4 Normal
random
variables . . .
91
3.5
The
Black-Scholes
formula.
. 94
3.6
The
Greeks of
European
options.
97
3.6.1 Explaining
the
magic
of
Greeks
computations
99
3.6.2 Implied volatility . . . . . . . . . . . . 103
3.7
The
concept of hedging.
~-
and
r-hedging
. 105
3.8 Implementation of
the
Black-Scholes
formula.
108
3.9 References 110
3.10
Exercises.
. . . . . . . . . . . . . . . . . . .
111
4
Lognormal
variables.
Risk-neutral
pricing.
117
4.1 Change of probability density for functions of
random
variables 117
4.2 Lognormal
random
variables . 119
4.3
Independent
random
variables . . . . . . . . . . . . . . . . . .
121
IX
4.4 Approximating sums of lognormal variables . 126
4.5 Power series . . . . . . . . . . . . . 128
4.5.1 Stirling's formula . . . . . . . . . 131
4.6 A lognormal model for asset prices
...
132
4.7
Risk-neutral
derivation
of
Black-Scholes 133
4.8
Probability
that
options expire in-the--money 135
4.9
Financial
Interpretation
of
N(d
1
)
and
N(d
2
)
137
4.10 References 138
4.11 Exercises . . . 139
5
Taylor's
formula.
Taylor
series.
143
5.1 Taylor's Formula for functions
of
one variable 143
5.2 Taylor's formula for multivariable
functions.
. 147
5.2.1 Taylor's formula for functions
of
two variables 150
5.3 Taylor series expansions
..
. . . . . . . . . 152
5.3.1 Examples
of
Taylor series expansions . 155
5.4 Greeks
and
Taylor's formula . . . . . . . . . . 158
5.5 Black-Scholes formula: ATM
approximations.
160
5.5.1 Several ATM approximations formulas 160
5.5.2 Deriving
the
ATM approximations formulas
161
5.5.3
The
precision of
the
ATM
approximation
of
the
Black-
Scholes formula . . . . . . . . . . . . . 165
5.6 Connections between
duration
and
convexity . 170
5.7 References 172
5.8
Exercises..................
173
6
Finite
Differences.
Black-Scholes
PDE.
177
6.1 Forward, backward, central finite differences 177
6.2
Finite
difference solutions of
ODEs
. . . . . 180
6.3
Finite
difference approximations for
Greeks.
190
6.4
The
Black-Scholes
PDE
. . . . . . . . . . .
191
6.4.1 Financial
interpretation
of
the
Black-Scholes
PDE
. 193
6.4.2
The
Black-Scholes
PDE
and
the
Greeks 194
6.5 References
6.6
Exercises......................
7
Multivariable
calculus:
chain
rule,
integration
by
substitu-
195
196
tion,
and
extrema.
203
7.1
Chain
rule for functions
of
several
variables.
. . . . . . . . . . 203

x
CONTENTS
7.2 Change of variables for double integrals
.....
.
7.2.1 Change of Variables
to
Polar
Coordinates.
7.3 Relative
extrema
of multivariable functions .
7.4
The
Theta
of a derivative security . .
7.5
Integrating
the
density function of Z
...
.
7.6
The
Box-Muller
method
..........
.
7.7
The
Black-Scholes
PDE
and
the
heat
equation.
7.8 Barrier options . . . . . . .
7.9
Optimality
of early exercise
7.10 References
7.11
Exercises.
. . . . .
8
Lagrange
multipliers.
Newton's
method.
Implied
volatil-
ity.
Bootstrapping.
8.1 Lagrange multipliers
..............
.
8.2 Numerical
methods
for 1-D nonlinear
problems.
8.2.1 Bisection
Method
8.2.2 Newton's
Method
............
.
8.2.3 Secant
Method
. . . . . . . . . . . . . .
8.3 Numerical
methods
for
N-dimensional
problems
8.3.1
The
N-dimensional
Newton's
Method
8.3.2
The
Approximate
Newton's
Method.
8.4
Optimal
investment portfolios
8.5
Computing
bond
yields . . . . . . . . . . .
8.6 Implied volatility
.............
.
8.7
Bootstrapping
for finding zero
rate
curves
8.8 References
8.9
Exercises.
Bibliography
Index
205
207
208
216
218
220
221
225
228
230
231
235
235
246
246
248
253
255
255
258
260
265
267
270
272
274
279
282
List
of
Tables
2.1
Pseudocode
for Midpoint
Rule.
. 59
2.2 Pseudocode for Trapezoidal Rule 59
2.3 Pseudocode for Simpson's Rule . 60
2.4 Pseudocode for computing
an
approximate
value of
an
integral
with
given tolerance
.........................
61
2.5 Pseudocode for computing
the
bond
price given
the
zero
rate
curve 74
2.6 Pseudocode for computing
the
bond
price given
the
instantaneous
interest
rate
curve
..........................
75
2.7 Pseudocode for computing
the
price,
duration
and
convexity of a
bond
given
the
yield
of
the
bond
...............
77
3.1 Pseudocode for
computing
the
cumulative
distribution
of Z 109
3.2 Pseudocode for Black-Scholes formula 109
8.1 Pseudocode for
the
Bisection
Method
247
8.2 Pseudocode for Newton's
Method.
. 250
8.3 Pseudocode for
the
Secant
Method
. 254
8.4 Pseudocode for
the
N-dimensional
Newton's
Method
257
8.5 Pseudocode for
the
N-dimensional
Approximate
Newton's
Method
259
8.6 Pseudocode for computing a
bond
yield.
. . 266
8.7 Pseudocode for
computing
implied volatility . . . . . . . . . . . . 269
Xl

Preface
The
use
of
quantitative
models
in
trading
has
grown
tremendously
in
recent
years,
and
seems likely
to
grow
at
similar speeds
in
the
future, due
to
the
availability
of
ever faster
and
cheaper
computing
power. Although
many
books
are
available for anyone
interested
in
learning
about
the
mathematical
models
used
in
the
financial industry,
most
of
these
books
target
either
the
finance
practitioner,
and
are
lighter
on
rigorous
mathematical
fundamentals,
or
the
academic scientist,
and
use high-level
mathematics
without
a clear
presentation
of
its
direct financial applications.
This
book
is
meant
to
build
the
solid
mathematical
foundation
required
to
understand
these
quantitative
models, while
presenting
a large
number
of
financial applications. Examples range from
Put-Call
parity,
bond
duration
and
convexity,
and
the
Black-Scholes model,
to
more
advanced topics, such as
the
numerical
estimation
of
the
Greeks, implied volatility,
and
bootstrapping
for finding
interest
rate
curves.
On
the
mathematical
side, useful
but
some-
times overlooked topics
are
presented
in
detail: differentiating integrals
with
respect
to
nonconstant
integral limits, numerical
approximation
of
definite
integrals, convergence
of
Taylor series, finite difference approximations, Stir-
ling's formula,
Lagrange
multipliers,
polar
coordinates,
and
Newton's
method
for multidimensional problems.
The
book
was designed so
that
someone
with
a solid knowledge
of
Calculus should
be
able
to
understand
all
the
topics pre-
sented.
Every
chapter
concludes
with
exercises
that
are
a
mix
of
mathematical
and
financial questions,
with
comments
regarding
their
relevance
to
practice
and
to
more
advanced topics.
Many
of
these
exercises are,
in
fact, questions
that
are frequently asked
in
interviews for
quantitative
jobs
in
financial in-
stitutions,
and
some
are
constructed
in
a sequential fashion, building
upon
each
other,
as is
often
the
case
at
interviews.
Complete
solutions
to
most
of
the
exercises
can
be
found
at
http://www.fepress.org/
This
book
can
be
used as a companion
to
any
more
advanced
quantitative
finance book.
It
also makes a good reference
book
for
mathematical
topics
that
are
frequently assumed
to
be
known
in
other
texts,
such as Taylor expan-
sions, Lagrange multipliers, finite difference approximations,
and
numerical
methods
for solving nonlinear equations.
This
book
should
be
useful
to
a large audience:
• Prospective
students
for financial engineering (or
mathematical
finance)
xiii

xiv
PREFACE
programs
will find
that
the
knowledge
contained
in
this
book
is
fundamental
for
their
understanding
of more advanced courses
on
numerical
methods
for
finance
and
stochastic calculus, while
some
of
the
exercises will give
them
a
flavor
of
what
interviewing for
jobs
upon
graduation
might
be
like.
• For finance practitioners, while
parts
of
the
book
will
be
light reading,
the
book
will also provide new
mathematical
connections (or present
them
in
a
new
light) between financial
instruments
and
models used
in
practice,
and
will
do
so
in
a rigorous
and
concise
manner.
•
For
academics teaching financial
mathematics
courses,
and
for
their
stu-
dents,
this
is a rigorous reference
book
for
the
mathematical
topics required
in
these
courses.
•
For
professionals interested
in
a career
in
finance
with
emphasis
on
quan-
titative
skills,
the
book
can
be
used
as a
stepping
stone
toward
that
goal,
by
building a solid
mathematical
foundation
for
further
studies, as well as
providing a first insight
in
the
world
of
quantitative
finance.
The
material
in
this
book
has
been
used
for a
mathematics
refresher course
for
students
entering
the
Financial Engineering
Masters
Program
(MFE)
at
Baruch
College,
City
University
of
New York.
Studying
this
material
be-
fore
entering
the
program
provided
the
students
with
a solid background
and
played
an
important
role
in
making
them
successful graduates: over 90
per-
cent
of
the
graduates
of
the
Baruch
MFE
Program
are
currently
employed
in
the
financial industry.
The
author
has
been
the
Director
of
the
Baruch
College
MFE
Program
1
since
its
inception
in
2002.
This
position
gave
him
the
privilege
to
inter-
act
with
generations of
students,
who were exceptional
not
only
in
terms
of
knowledge
and
ability,
but
foremost as
very
special friends
and
colleagues.
The
connection
built
during
their
studies
has
continued over
the
years,
and
as
alumni
of
the
program
their
contribution
to
the
continued success
of
our
students
has
been
tremendous.
This
is
the
first
in
a series of
books
containing
mathematical
background
needed for financial engineering applications,
to
be
followed
by
books
in
N u-
merical
Linear
Algebra, Probability,
and
Differential Equations.
Dan
Stefanica
New York, 2008
IBaruch
MFE
Program
web page:
http://www.baruch.cuny.edu/math/masters.html
QuantNetwork student forum web page:
http://www.quantnet.org/forum/index.php
Acknow
ledgments
I have
spent
several wonderful years
at
Baruch
College, as Director
of
the
Financial Engineering Masters
Program.
Working
with
so
many
talented
students
was a privilege, as well as a learning experience
in
itself,
and
see-
ing a
strong
community
develop
around
the
MFE
program
was incredibly
rewarding.
This
book
is
by
all accounts a direct
result
of interacting
with
our
students
and
alumni,
and
I
am
truly
grateful
to
all
of
them
for this.
The
strong
commitment
of
the
administration
of
Baruch
College
to
sup-
port
the
MFE
program
and
provide
the
best
educational
environment
to
our
students
was essential
to
all
aspects
of
our
success,
and
permeated
to
creating
the
opportunity
for
this
book
to
be
written.
I
learned
a
lot
from working alongside
my
colleagues
in
the
mathematics
department
and
from
many
conversations
with
practitioners
from
the
finan-
cial
industry
..
Special
thanks
are
due
to
Elena
Kosygina
and
Sherman Wong,
as well as
to
my
good
friends
Peter
Carr
and
Salih Neftci.
The
title
of
the
book
was suggested
by
Emanuel
Derman,
and
is
more
euphonious
than
any
previously considered alternatives.
Many
students
have looked over
ever-changing
versions of
the
book,
and
their
help
and
encouragement were
greatly
appreciated.
The
knowledgeable
comments
and
suggestions
of
Robert
Spruill
are
reflected
in
the
final ver-
sion
of
the
book, as
are
exercises suggested
by
Sudhanshu
Pardasani.
Andy
Nguyen
continued
his
tremendous
support
both
on
QuantNet.org,
hosting
the
problems solutions,
and
on
the
fepress.org website.
The
art
for
the
book
cover is
due
to
Max
Rumyantsev.
The
final effort
of
proofreading
the
mate-
rial was
spareheaded
by
Vadim Nagaev,
Muting
Ren,
Rachit
Gupta,
Claudia
Li, Sunny Lu,
Andrey
Shvets, Vic Siqiao,
and
Frank
Zheng.
I would have never
gotten
past
the
lecture
notes
stage
without
tremen-
dous
support
and
understanding
from my family.
Their
smiling presence
and
unwavering
support
brightened
up
my
efforts
and
made
them
worthwhile.
This
book
is
dedicated
to
the
two ladies
in
my
life.
Dan
Stefanic a
New York, 2008
xv

How
to
Use
This
Book
While
we
expect
a large audience
to
find
this
book
useful,
the
approach
to
reading
the
book
will
be
different
depending
on
the
background
and
goals
of
the
reader.
Prospective
students
for financial engineering
or
mathematical
finance pro-
grams
should find
the
study
of
this
book
very
rewarding, as
it
will give
them
a
head
start
in
their
studies,
and
will provide a reference
book
throughout
their
course
of
study. Building a solid
base
for
further
study
is of
tremen-
dous
importance.
This
book
teaches core concepts
important
for a successful
learning experience
in
financial engineering
graduate
programs.
Instructors
of
quantitative
finance courses will find
the
mathematical
topics
and
their
treatment
to
be
of
greatest
value,
and
could use
the
book
as a
reference
text
for a
more
advanced
treatment
of
the
mathematical
content
of
the
course
they
are
teaching.
Instructors
of
financial
mathematics
courses will find
that
the
exercises
in
the
book
provide novel assignment ideas. Also, some topics might
be
non-
traditional
for
such
courses,
and
could
be
useful
to
include
or
mention
in
the
course.
Finance
practitioners
should enjoy
the
rigor
of
the
mathematical
presentation,
while finding
the
financial examples interesting,
and
the
exercises a
potential
source for interview questions.
The
book
was
written
with
the
aim
of
ensuring
that
anyone thoroughly
studying
it
will have a
strong
base for
further
study
and
full
understanding
of
the
mathematical
models used
in
finance.
A
point
of
caution:
there
is a significant difference between
studying
a
book
and
merely reading it. To benefit fully from
this
book, all exercises
should
be
attempted,
and
the
material
should
be
learned as if for
an
exam.
Many
of
the
exercises have
particular
relevance for people who will inter-
view for
quantitative
jobs,
as
they
have a flavor similar
to
questions
that
are
currently
asked
at
such interviews.
The
book
is sequential
in
its
presentation,
with
the
exception
of
Chapter
0, which
can
be
skipped
over
and
used as a collection
of
reference topics.
XVll

xviii
HOW
TO
USE
THIS
BOOK
Chapter
0
Mathematical
preliminaries
Even
and
odd
functions.
Useful
sums
with
interesting proofs.
Sequences satisfying linear recursions.
The
"Big
0"
and
"little
0"
notations.
This
chapter
is a collection
of
topics
that
are
needed
later
on
in
the
book,
and
may
be
skipped
over
in
a first reading.
It
is also
the
only
chapter
of
the
book
where no financial applications are presented.
Nonetheless, some
of
the
topics
in
this
chapter
are
rather
subtle
from a
mathematical
standpoint,
and
understanding
their
treatment
is instructive.
In
particular,
we include a discussion of
the
"Big
0"
and
"little
0"
notations,
i.e.,
0(·)
and
0('), which are often a source
of
confusion.
0.1
Even
and
odd
functions
Even
and
odd
functions are special families
of
functions whose graphs exhibit
special symmetries. We present several simple
properties
of
these
functions
which will
be
used subsequently.
Definition
0.1.
The
function
f :
~
-7
~ is an even
function
if
and only
if
f(
-x)
=
f(x),
V x E
~.
(1)
The
graph
of
any
even function is
symmetric
with
respect
to
the
y-axis.
Example:
The
density
function f
(x)
of
the
standard
normal
variable, i.e.,
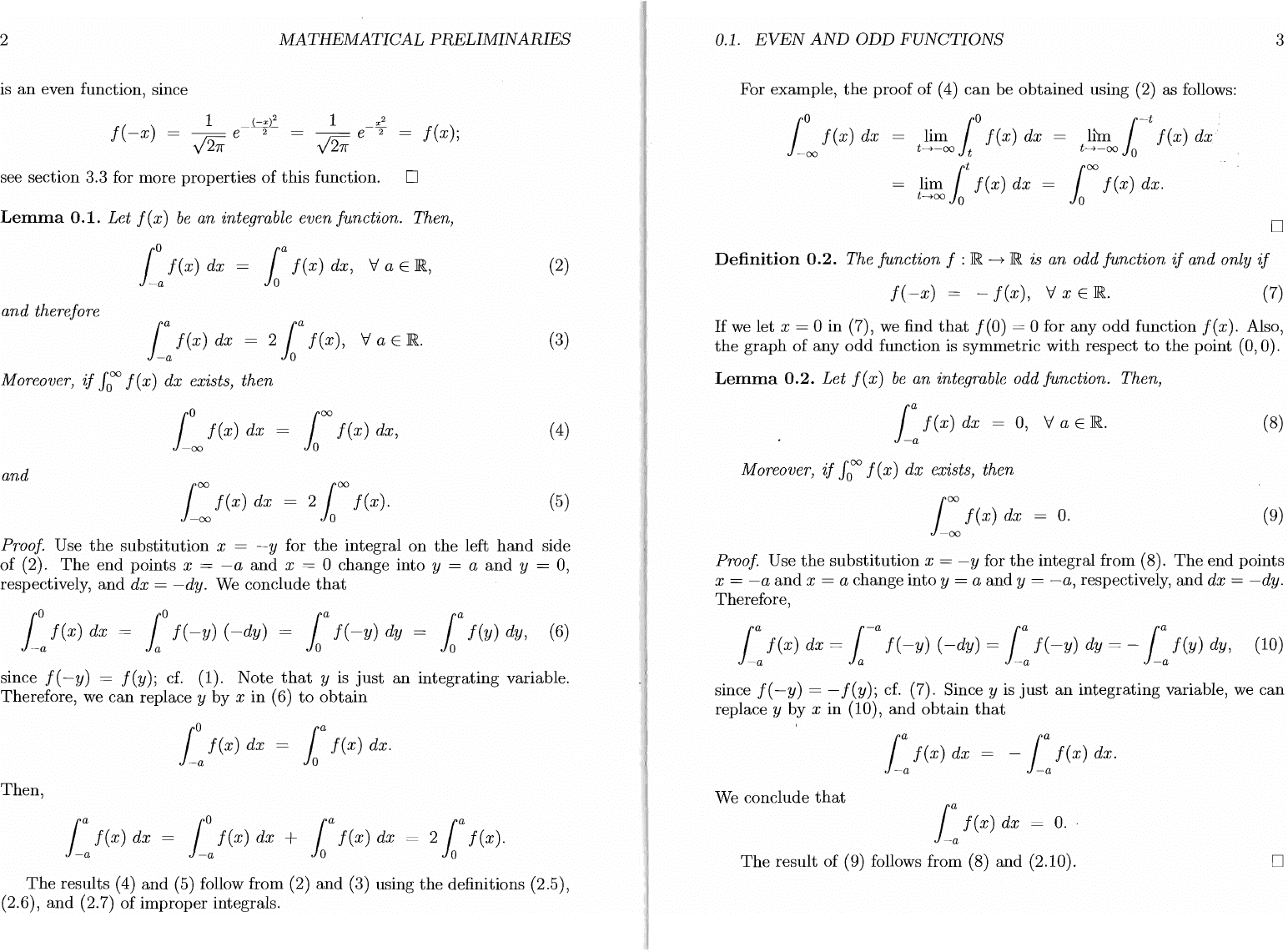
2
MATHEMATICAL
PRELIMINARIES
is
an
even function, since
1
_(_x)2
f(-x)
=
-e
2
V2ir
see section 3.3 for more properties
of
this
function.
= f(x);
o
Lemma
0.1.
Let
f(x)
be
an
integrable
even
function. Then,
1:
j(
x) dx =
1"
j (x) dx, V a E
R.,
and
therefore
I:
j (x) dx = 2
1"
j (x), V a E
R..
Moreover,
if
Jo
oo
f (x)
dx
exists,
then
I:
j(x)
dx =
f'
j(x)
dx,
and
I:
j(x)
dx = 2
f'
j(x).
(2)
(3)
(4)
(5)
Proof. Use
the
substitution
x =
-y
for
the
integral
on
the
left
hand
side
of (2).
The
end
points x =
-a
and
x = 0 change into y = a
and
y = 0,
respectively,
and
dx
=
-dy.
We conclude
that
1
0
f(x)
dx
= r
O
f(
-v)
(-dy)
= r
a
f(
-v)
dy
= r
a
f(y)
dy, (6)
-a
Ja Jo Jo
since
f(
-V)
=
f(y);
cf.
(1). Note
that
y is
just
an
integrating variable.
Therefore, we can replace
y by x
in
(6)
to
obtain
1:
j(x)
dx =
1"
j(x)
dx.
Then,
t
j(x)
dx =
1:
j(x)
dx +
1"
j(x)
dx =
21"
j(x).
The
results (4)
and
(5) follow from (2)
and
(3) using
the
definitions (2.5),
(2.6),
and
(2.7) of improper integrals.
0.1.
EVEN
AND
ODD
FUNCTIONS
3
For example,
the
proof of (4)
can
be
obtained
using (2) as follows:
I:
j(x)
dx =
1
0
l-t
lim
f(x)
dx
=
Hm
f(x)
dx
t-+-oo
t
t-+-oo
0
lim
(t
f(x)
dx
=
roo
f(x)
dx.
t-+oo
Jo
Jo
D
Definition
0.2.
The
function
f :
JR
---+
JR
is
an
odd
function
if
and only
if
f(-x)
= -
f(x),
V x E
JR.
(7)
If
we let x = 0
in
(7), we find
that
f(O) = 0 for
any
odd
function
f(x).
Also,
the
graph
of
any
odd
function is symmetric
with
respect
to
the
point (0,0).
Lemma
0.2.
Let
f(x)
be
an
integrable odd
function.
Then,
I:
j(x)
dx =
0,
V a E
R..
(8)
Moreover,
if
Jo
oo
f (
x)
dx
exists,
then
1:
j(x)
dx =
o.
(9)
Proof. Use
the
substitution
x =
-y
for
the
integral from (8).
The
end points
x =
-a
and
x = a change into y = a
and
y =
-a,
respectively,
and
dx
=
-dy.
Therefore,
since
f(
-V)
= -
f(y);
cf. (7). Since y is
just
an
integrating
variable, we can
replace
y
by
x in (10),
and
obtain
that
t
j(x)
dx = - t
j(x)
dx.
We conclude
that
I:
j(x)
dx = O
..
The
result of (9) follows from (8)
and
(2.10).
D
