Stewart J. Calculus
Подождите немного. Документ загружается.

If F is integrable over R, then we define the double integral of over D by
Definition 2 makes sense because R is a rectangle and so has been previ-
ously defined in Section 16.1. The procedure that we have used is reasonable because the
values of are 0 when lies outside and so they contribute nothing to the inte-
gral. This means that it doesn’t matter what rectangle we use as long as it contains .
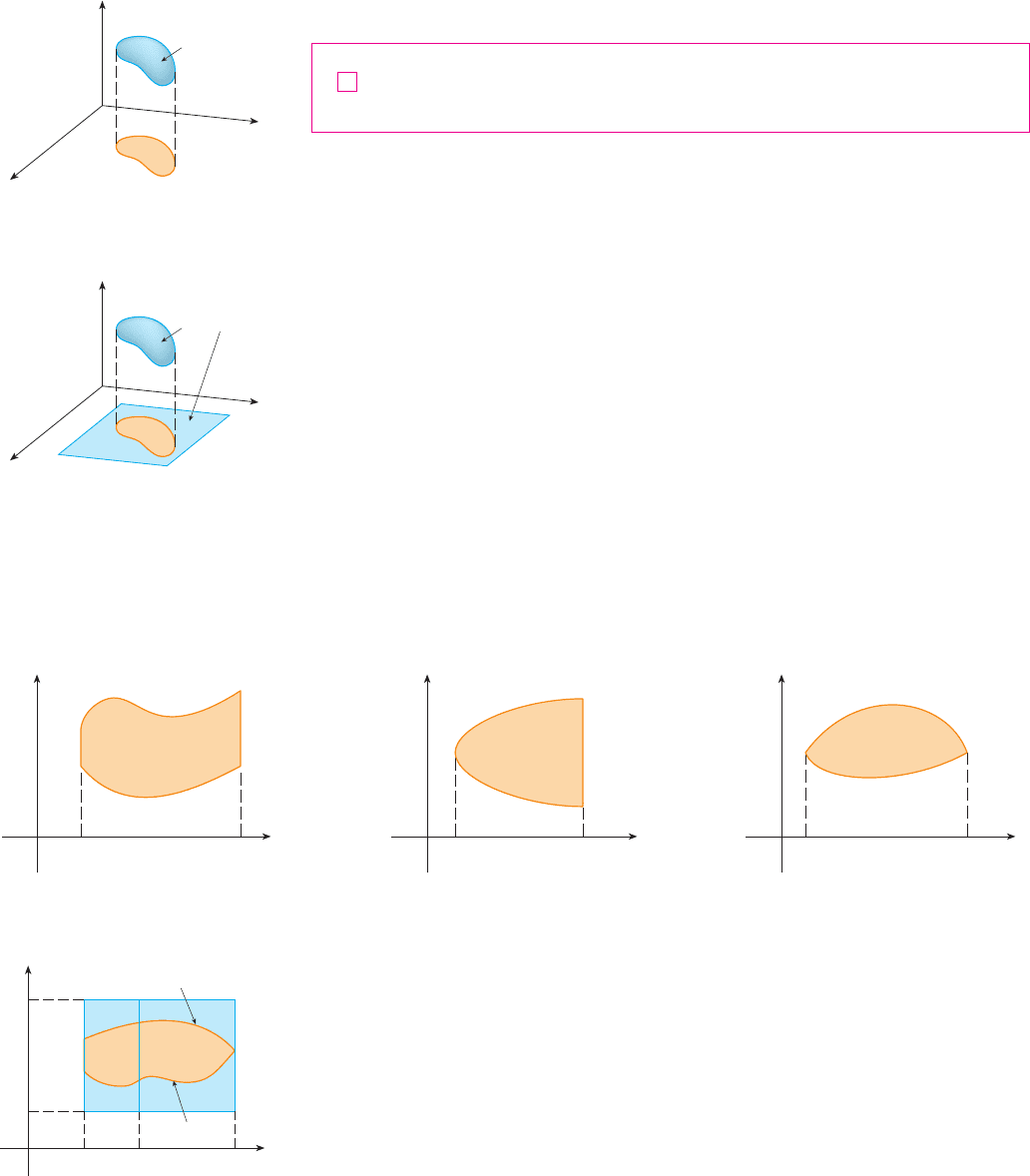
In the case where , we can still interpret as the volume of the
solid that lies above and under the surface (the graph of ). You can see that
this is reasonable by comparing the graphs of and in Figures 3 and 4 and remember-
ing that is the volume under the graph of .
Figure 4 also shows that is likely to have discontinuities at the boundary points of
Nonetheless, if is continuous on and the boundary curve of is “well behaved”
(in a sense outside the scope of this book), then it can be shown that exists
and therefore exists. In particular, this is the case for the following types
of regions.
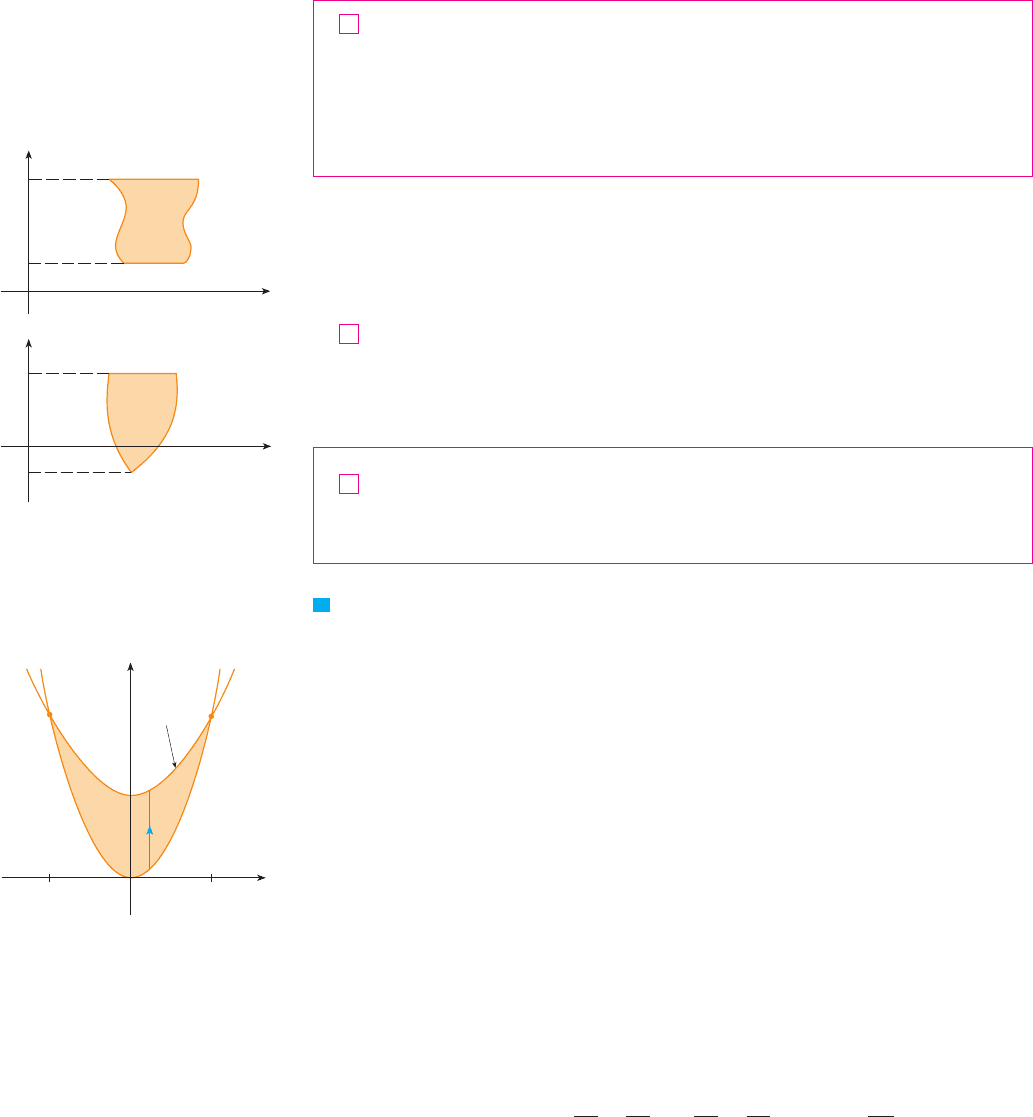
A plane region is said to be of type I if it lies between the graphs of two continuous
functions of , that is,
where and are continuous on . Some examples of type I regions are shown in
Figure 5.
In order to evaluate when is a region of type I, we choose a rectangle
that contains , as in Figure 6, and we let be the function given by
Equation 1; that is, agrees with on and is outside . Then, by Fubini’s Theorem,
Observe that if or because then lies outside .
Therefore
y
d
c
F共x, y兲 dy 苷
y
t
2
共x兲
t
1
共x兲
F共x, y兲 dy 苷
y
t
2
共x兲
t
1
共x兲
f 共x, y兲 dy
D共x, y兲y t
2
共x兲y
t
1
共x兲F共x, y兲 苷 0
yy
D
f 共x, y兲 dA 苷
yy
R
F共x, y兲 dA 苷
y
b
a
y
d
c
F共x, y兲 dy dx
D0FDfF
FDR 苷 关a, b兴 关c, d兴
D
xx
D
f 共x, y兲 dA
FIGURE 5 Some type I regions
0
y
x
ba
D
y=g™(x)
y=g¡(x)
0
y
x
ba
D
y=g™(x)
y=g¡(x)
0
y
x
ba
D
y=g™(x)
y=g¡(x)
关a, b兴t
2
t
1
D 苷 兵共x, y兲
ⱍ
a x b, t
1
共x兲 y t
2
共x兲其
x
D
xx
D
f 共x, y兲 dA
xx
R
F共x, y兲 dA
DDfD.
F
Fxx
R
F共x, y兲 dA
Ff
fz 苷 f 共x, y兲D
xx
D
f 共x, y兲 dAf 共x, y兲 0
DR
D共x, y兲F共x, y兲
xx
R
F共x, y兲 dA
where F is given by Equation 1
yy
D
f 共x, y兲 dA 苷
yy
R
F共x, y兲 dA
2
f
1002
||||
CHAPTER 16 MULTIPLE INTEGRALS
y
0
z
x
D
graph of f
FIGURE 4
y
0
z
x
D
graph of F
FIGURE 3
FIGURE 6
d
0
x
y
bx
a
c
y=g¡(x)
D
y=g™(x)
because when . Thus we have the following formula
that enables us to evaluate the double integral as an iterated integral.
If is continuous on a type I region D such that
then
The integral on the right side of (3) is an iterated integral that is similar to the ones we
considered in the preceding section, except that in the inner integral we regard as being
constant not only in but also in the limits of integration, and
We also consider plane regions of type II, which can be expressed as
where and are continuous. Two such regions are illustrated in Figure 7.
Using the same methods that were used in establishing (3), we can show that
where D is a type II region given by Equation 4.
EXAMPLE 1 Evaluate , where is the region bounded by the
parabolas and .
SOLUTION The parabolas intersect when , that is, , so . We
note that the region , sketched in Figure 8, is a type I region but not a type II region
and we can write
Since the lower boundary is and the upper boundary is , Equation 3
gives
M
苷 3
x
5
5
x
4
4
2
x
3
3
x
2
2
x
册
1
1
苷
32
15
苷
y
1
1
共3x
4
x
3
2x
2
x 1兲 dx
苷
y
1
1
关x共1 x
2
兲 共1 x
2
兲
2
x共2x
2
兲 共2x
2
兲
2
兴
dx
苷
y
1
1
[
xy y
2
]
y苷2x
2
y苷1x
2
dx
yy
D
共x 2y兲 dA 苷
y
1
1
y
1x
2
2x
2
共x 2y兲 dy dx
y 苷 1 x
2
y 苷 2x
2
D 苷
兵
共x, y兲
ⱍ
1 x 1, 2x
2
y 1 x
2
其
D
x 苷 1x
2
苷 12x
2
苷 1 x
2
y 苷 1 x
2
y 苷 2x
2
Dxx
D
共x 2y兲 dA
V
yy
D
f 共x, y兲 dA 苷
y
d
c
y
h
2
共 y兲
h
1
共 y兲
f 共x, y兲 dx dy
5
h
2
h
1
D 苷
兵
共x, y兲
ⱍ
c y d, h
1
共y兲 x h
2
共y兲
其
4
t
2
共x兲.t
1
共x兲f 共x, y兲
x
yy
D
f 共x, y兲 dA 苷
y
b
a
y
t
2
共x兲
t
1
共x兲
f 共x, y兲 dy dx
D 苷
兵
共x, y兲
ⱍ
a x b, t
1
共x兲 y t
2
共x兲
其
f
3
t
1
共x兲 y t
2
共x兲F共x, y兲 苷 f 共x, y兲
SECTION 16.3 DOUBLE INTEGRALS OVER GENERAL REGIONS
||||
1003
FIGURE 7
Some type II regions
d
0
x
y
c
x=h¡(y)
x=h¡(y)
D
x=h™(y)
x=h™(y)
d
0
x
y
c
D
x
1
_1
y
(_1,2)
(1,2)
D
y=2≈
y=1+≈
FIGURE 8
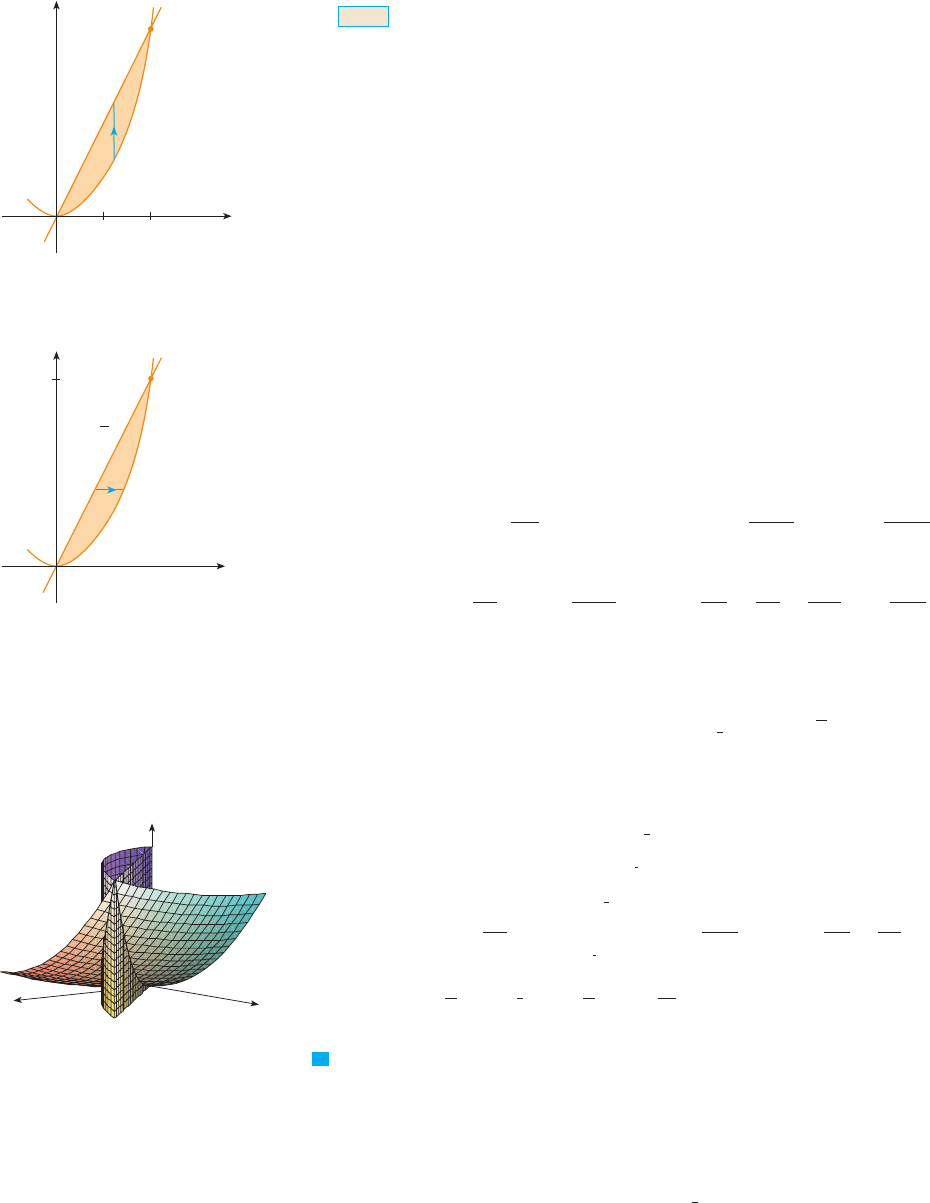
When we set up a double integral as in Example 1, it is essential to draw a
diagram. Often it is helpful to draw a vertical arrow as in Figure 8. Then the limits of
integration for the inner integral can be read from the diagram as follows: The arrow
starts at the lower boundary , which gives the lower limit in the integral, and
the arrow ends at the upper boundary , which gives the upper limit of integration.
For a type II region the arrow is drawn horizontally from the left boundary to the right
boundary.
EXAMPLE 2 Find the volume of the solid that lies under the paraboloid and
above the region in the -plane bounded by the line and the parabola .
SOLUTION 1 From Figure 9 we see that is a type I region and
Therefore the volume under and above is
SOLUTION 2 From Figure 10 we see that can also be written as a type II region:
Therefore another expression for is
M
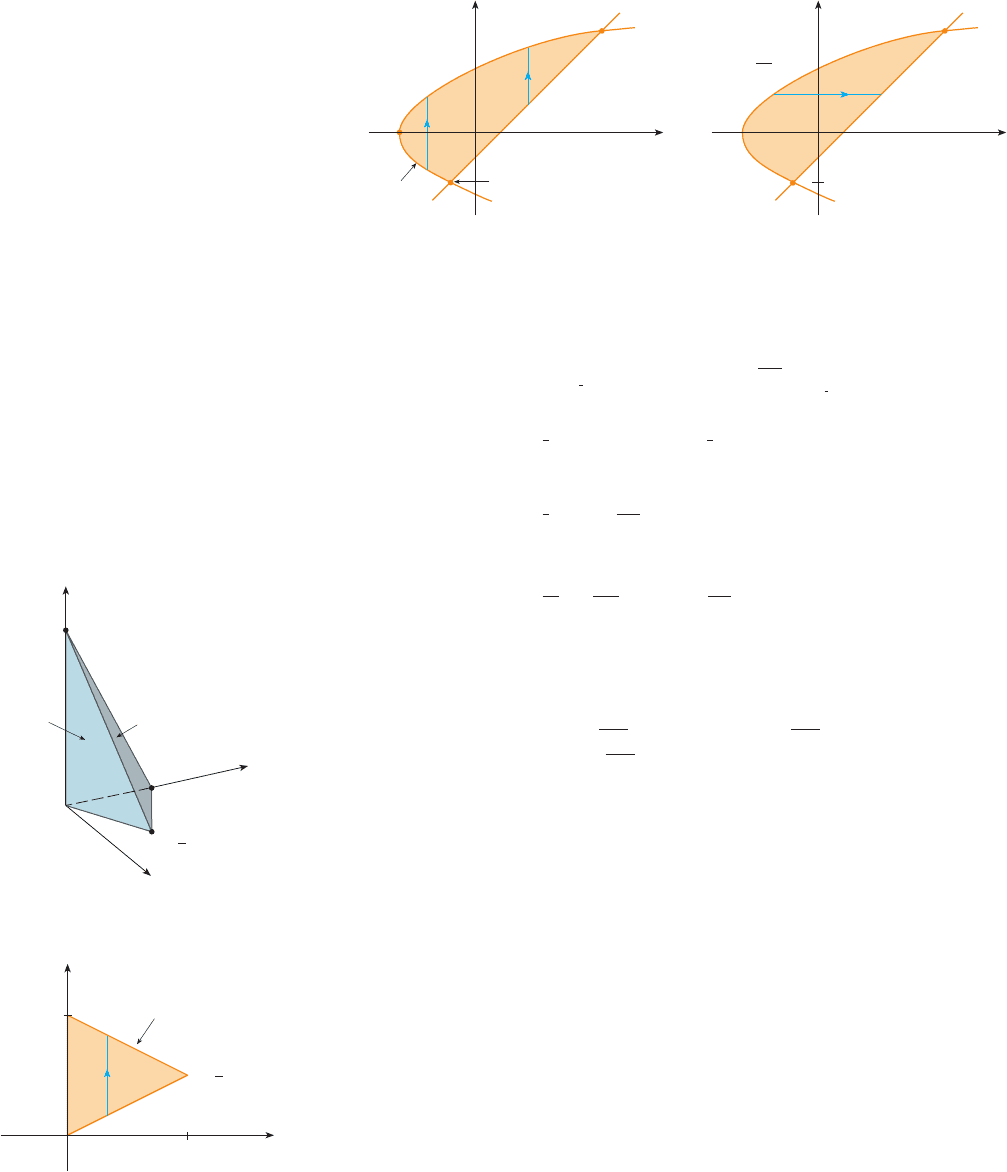
EXAMPLE 3 Evaluate where is the region bounded by the line
and the parabola .
SOLUTION The region is shown in Figure 12. Again is both type I and type II, but the
description of as a type I region is more complicated because the lower boundary con-
sists of two parts. Therefore we prefer to express as a type II region:
D 苷
兵
(x, y)
ⱍ
2 y 4,
1
2
y
2
3 x y 1
其
D
D
DD
y
2
苷 2x 6
y 苷 x 1Dxx
D
xy dA,
V
苷
2
15
y
5兾2
2
7
y
7兾2
13
96
y
4
]
0
4
苷
216
35
苷
y
4
0
冋
x
3
3
y
2
x
册
x苷
1
2
y
x苷
s
y
dy 苷
y
4
0
冉
y
3兾2
3
y
5兾2
y
3
24
y
3
2
冊
dy
V 苷
yy
D
共x
2
y
2
兲
dA 苷
y
4
0
y
s
y
1
2
y
共x
2
y
2
兲
dx dy
V
D 苷
兵
共x, y兲
ⱍ
0 y 4,
1
2
y x
s
y
其
D
苷
y
2
0
冉
x
6
3
x
4
14x
3
3
冊
dx 苷
x
7
21
x
5
5
7x
4
6
册
0
2
苷
216
35
苷
y
2
0
冋
x
2
y
y
3
3
册
y苷x
2
y苷2x
dx 苷
y
2
0
冋
x
2
共2x兲
共2x兲
3
3
x
2
x
2
共x
2
兲
3
3
册
dx
V 苷
yy
D
共x
2
y
2
兲
dA 苷
y
2
0
y
2x
x
2
共x
2
y
2
兲
dy dx
Dz 苷 x
2
y
2
D 苷
兵
共x, y兲
ⱍ
0 x 2, x
2
y 2x
其
D
y 苷 x
2
y 苷 2xxyD
z 苷 x
2
y
2
y 苷 t
2
共x兲
y 苷 t
1
共x兲
NOTE
1004
||||
CHAPTER 16 MULTIPLE INTEGRALS
FIGURE 10
D as a type II region
FIGURE 9
D as a type I region
y
0
x
12
(2,4)
D
y=≈
y=2x
x=œ
„
y
1
2
x= y
y
4
0
x
D
(2,4)
N Figure 11 shows the solid whose volume
is calculated in Example 2. It lies above the
-plane, below the paraboloid ,
and between the plane and the
parabolic cylinder .y 苷 x
2
y 苷 2x
z 苷 x
2
y
2
xy
FIGURE 11
y
x
z
z=≈+¥
y=2x
y=≈
Then (5) gives
If we had expressed as a type I region using Figure 12(a), then we would have
obtained
but this would have involved more work than the other method. M
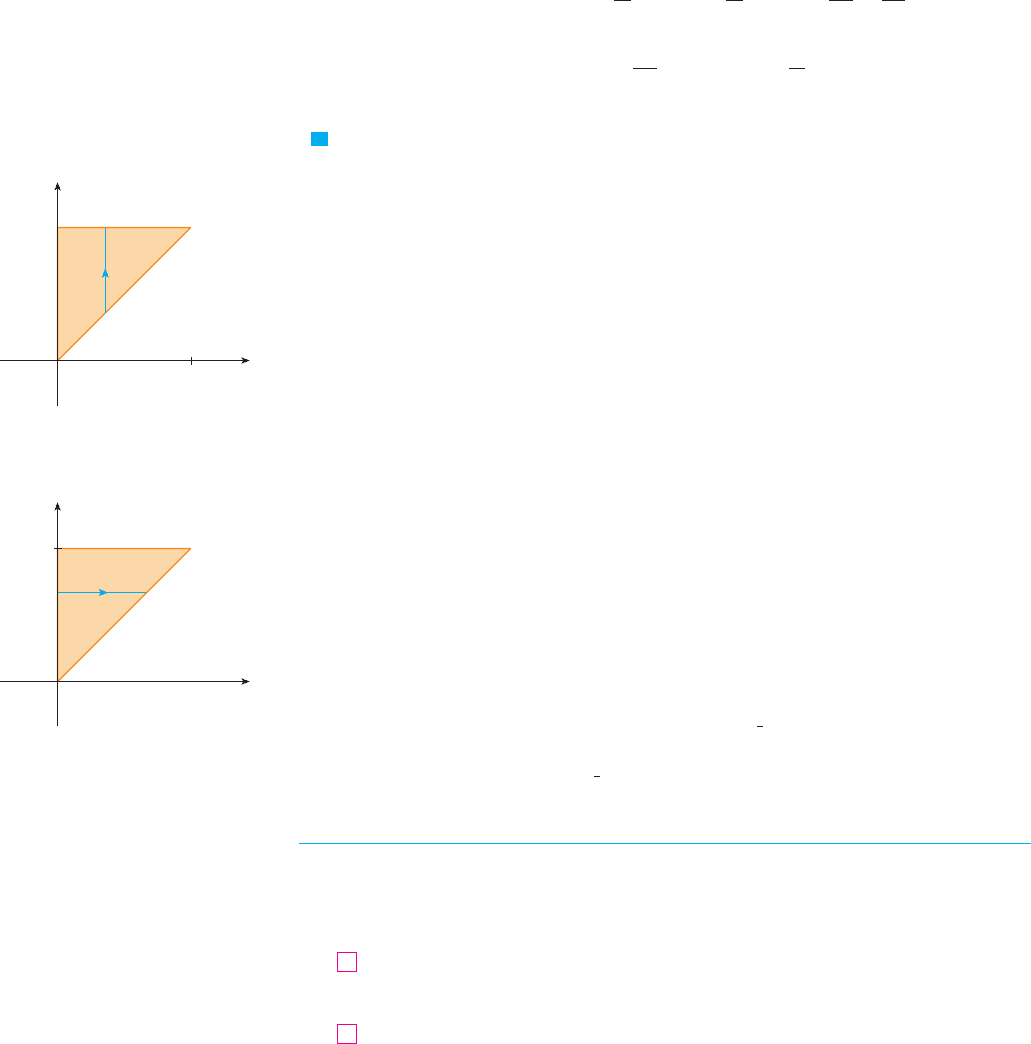
EXAMPLE 4 Find the volume of the tetrahedron bounded by the planes ,
, , and .
SOLUTION In a question such as this, it’s wise to draw two diagrams: one of the three-
dimensional solid and another of the plane region over which it lies. Figure 13 shows
the tetrahedron bounded by the coordinate planes , , the vertical plane
, and the plane . Since the plane intersects the
-plane (whose equation is ) in the line , we see that lies above the
triangular region in the -plane bounded by the lines , , and .
(See Figure 14.)
The plane can be written as , so the required volume
lies under the graph of the function and above
D 苷
兵
共x, y兲
ⱍ
0 x 1, x兾2 y 1 x兾2
其
z 苷 2 x 2y
z 苷 2 x 2yx 2y z 苷 2
x 苷 0x 2y 苷 2x 苷 2yxyD
Tx 2y 苷 2z 苷 0xy
x 2y z 苷 2x 2y z 苷 2x 苷 2y
z 苷 0x 苷 0T
D
z 苷 0x 苷 0x 苷 2y
x 2y z 苷 2
yy
D
xy dA 苷
y
1
3
y
s
2x6
s
2x6
xy dy dx
y
5
1
y
s
2x6
x1
xy dy dx
D
苷
1
2
冋
y
6
24
y
4
2
y
3
3
4y
2
册
2
4
苷 36
苷
1
2
y
4
2
冉
y
5
4
4y
3
2y
2
8y
冊
dy
苷
1
2
y
4
2
y
[
共y 1兲
2
(
1
2
y
2
3
)
2
]
dy
yy
D
xy dA 苷
y
4
2
y
y1
1
2
y
2
3
xy dx dy 苷
y
4
2
冋
x
2
2
y
册
x苷
1
2
y
2
3
x苷y1
dy
FIGURE 12
(5,4)
0
y
x
_3
y=x-1
(_1,_2)
y=_œ„„„„
„
2x+6
(a) D as a type I region (b) D as a type II region
x=-3
¥
2
(5,4)
x=y+1
(_1,_2)
0
y
x
_2
y=œ„„„„
„
2x+6
SECTION 16.3 DOUBLE INTEGRALS OVER GENERAL REGIONS
||||
1005
FIGURE 14
FIGURE 13
y=x/2
”1, ’
1
2
D
y
0
1
x
1
(0,1,0)
(0,0,2)
y
x
0
z
x+2y+z=2
x=2y
”1, ,0’
1
2
T
(or y=1-x/2)
x+2y=2
Therefore
M
EXAMPLE 5 Evaluate the iterated integral .
SOLUTION If we try to evaluate the integral as it stands, we are faced with the task of first
evaluating . But it’s impossible to do so in finite terms since is
not an elementary function. (See the end of Section 8.5.) So we must change the order
of integration. This is accomplished by first expressing the given iterated integral as a
double integral. Using (3) backward, we have
where
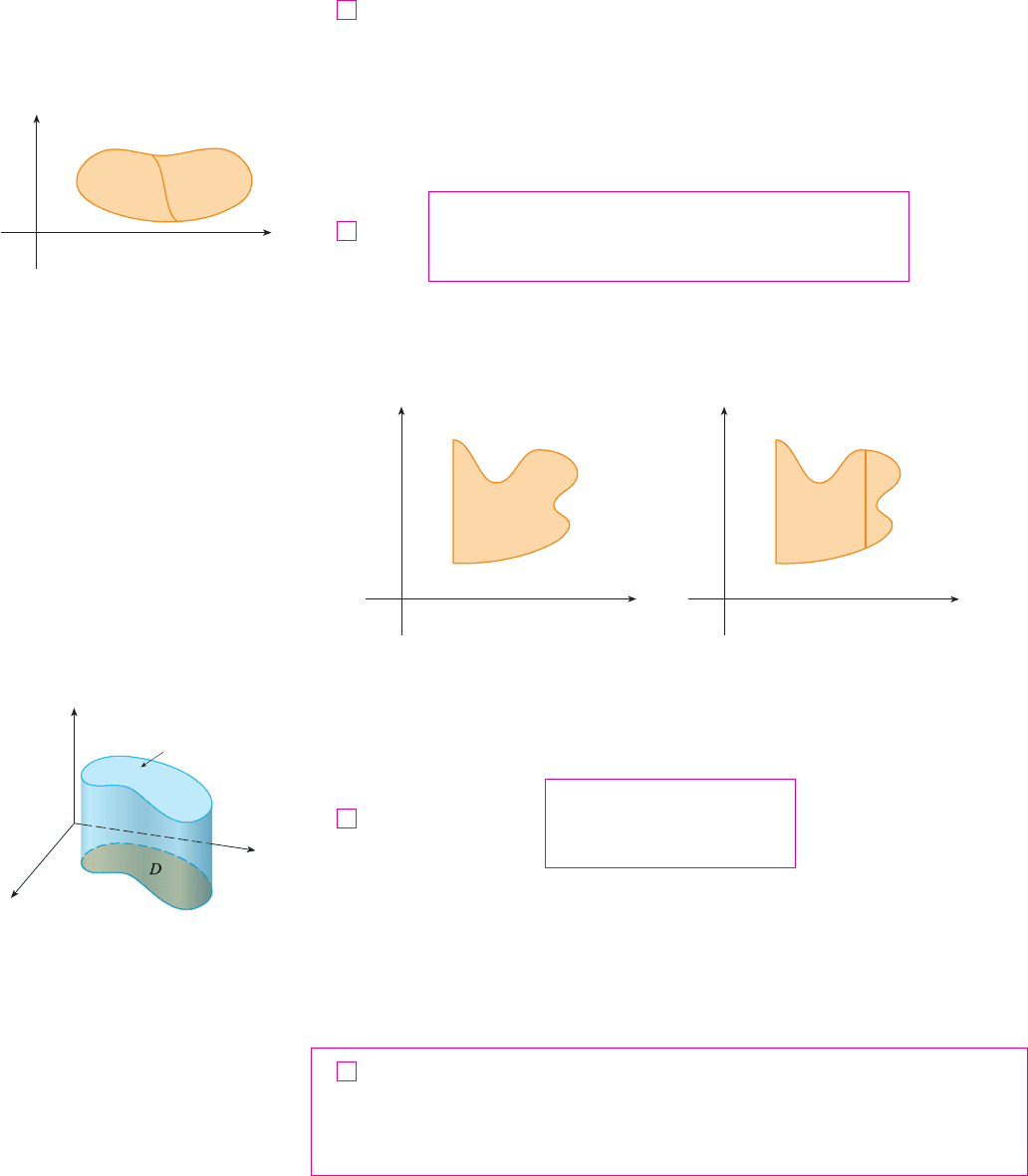
We sketch this region in Figure 15. Then from Figure 16 we see that an alternative
description of is
This enables us to use (5) to express the double integral as an iterated integral in the
reverse order:
M
PROPERTIES OF DOUBLE INTEGRALS
We assume that all of the following integrals exist. The first three properties of double inte-
grals over a region follow immediately from Definition 2 and Properties 7, 8, and 9 in
Section 16.1.
yy
D
cf共x, y兲 dA 苷 c
yy
D
f 共x, y兲 dA
7
yy
D
关 f 共x, y兲 t共x, y兲兴 dA 苷
yy
D
f 共x, y兲 dA
yy
D
t共x, y兲 dA
6
D
苷
1
2
共1 cos 1兲
苷
y
1
0
y sin共y
2
兲
dy 苷
1
2
cos共y
2
兲
]
0
1
苷
y
1
0
y
y
0
sin共y
2
兲
dx dy 苷
y
1
0
[
x sin共y
2
兲
]
x苷0
x苷y
dy
y
1
0
y
1
x
sin共y
2
兲
dy dx 苷
yy
D
sin共y
2
兲
dA
D 苷
兵
共x, y兲
ⱍ
0 y 1, 0 x y
其
D
D
D 苷
兵
共x, y兲
ⱍ
0 x 1, x y 1
其
y
1
0
y
1
x
sin共y
2
兲
dy dx 苷
yy
D
sin共y
2
兲
dA
x sin共y
2
兲
dyx sin共y
2
兲
dy
x
1
0
x
1
x
sin共y
2
兲
dy dx
V
苷
y
1
0
共x
2
2x 1兲 dx 苷
x
3
3
x
2
x
册
0
1
苷
1
3
苷
y
1
0
冋
2 x x
冉
1
x
2
冊
冉
1
x
2
冊
2
x
x
2
2
x
2
4
册
dx
苷
y
1
0
[
2y xy y
2
]
y苷x兾2
y苷1x兾2
dx
V 苷
yy
D
共2 x 2y兲 dA 苷
y
1
0
y
1x兾2
x兾2
共2 x 2y兲 dy dx
1006
||||
CHAPTER 16 MULTIPLE INTEGRALS
1
x
0
y
D
y=1
y=x
x
0
y
1
D
x=0
x=y
FIGURE 16
D as a type II region
FIGURE 15
D as a type I region
If for all in , then
The next property of double integrals is similar to the property of single integrals given
by the equation .
If , where and don’t overlap except perhaps on their boundaries
(see Figure 17), then
Property 9 can be used to evaluate double integrals over regions that are neither type I
nor type II but can be expressed as a union of regions of type I or type II. Figure 18 illus-
trates this procedure. (See Exercises 51 and 52.)
The next property of integrals says that if we integrate the constant function
over a region , we get the area of :
Figure 19 illustrates why Equation 10 is true: A solid cylinder whose base is and whose
height is 1 has volume , but we know that we can also write its volume
as .
Finally, we can combine Properties 7, 8, and 10 to prove the following property. (See
Exercise 57.)
If for all in , then
mA共D兲
yy
D
f 共x, y兲 dA MA共D兲
D共x, y兲m f 共x, y兲 M
11
xx
D
1 dA
A共D兲 ⴢ 1 苷 A共D兲
D
yy
D
1 dA 苷 A共D兲
10
DD
f 共x, y兲 苷 1
FIGURE 18
x
0
y
D
(a) D is neither type I nor type II.
x
0
y
D¡
D™
(b) D=D¡ 傼 D™, D¡ is type I, D™ is type II.
D
yy
D
f 共x, y兲 dA 苷
yy
D
1
f 共x, y兲 dA
yy
D
2
f 共x, y兲 dA
9
D
2
D
1
D 苷 D
1
傼 D
2
x
b
a
f 共x兲 dx 苷 x
c
a
f 共x兲 dx x
b
c
f 共x兲 dx
yy
D
f 共x, y兲 dA
yy
D
t共x, y兲 dA
8
D共x, y兲f 共x, y兲 t共x, y兲
SECTION 16.3 DOUBLE INTEGRALS OVER GENERAL REGIONS
||||
1007
0
y
x
D
D¡ D™
FIGURE 17
FI
G
URE 1
9
C
y
linder with base
D
and hei
g
ht
1
y
0
z
x
z=
1
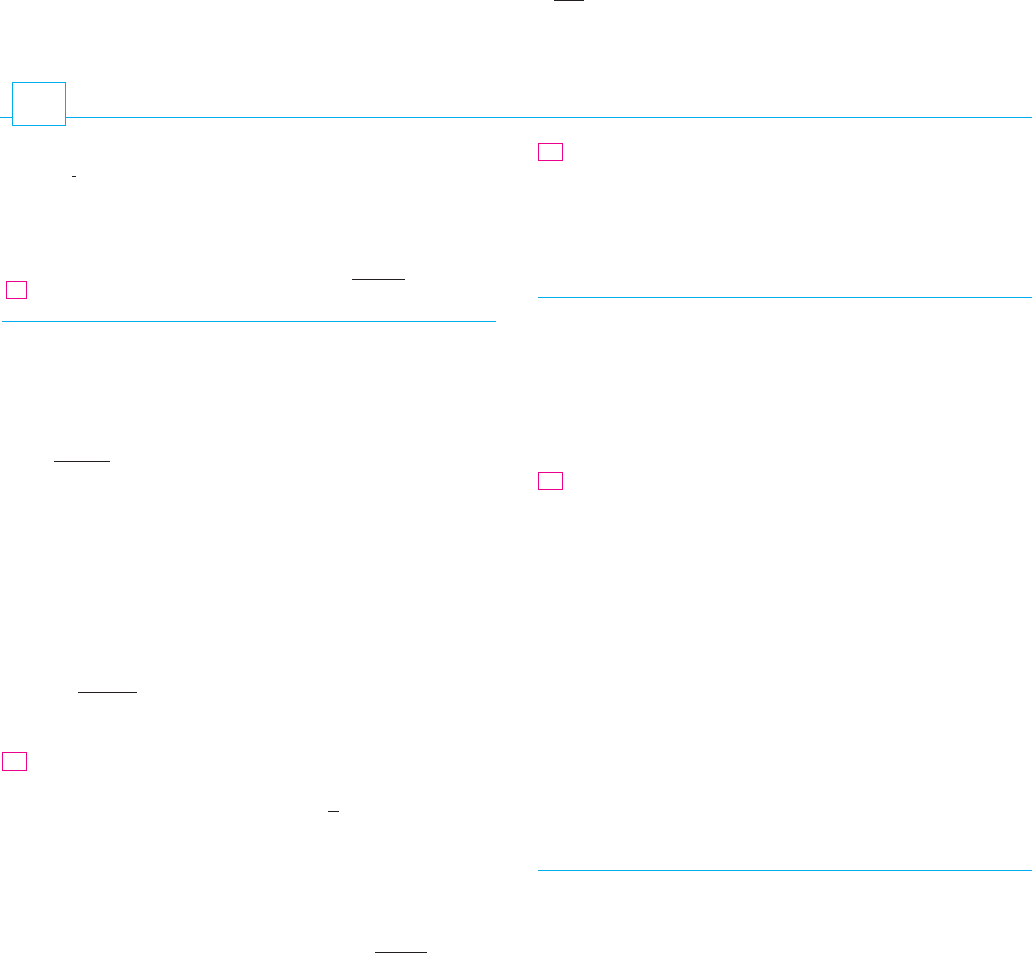
1008
||||
CHAPTER 16 MULTIPLE INTEGRALS
is bounded by the circle with center the origin and radius 2
18. is the triangular region with vertices ,
, and
19–28 Find the volume of the given solid.
19. Under the plane and above the region
bounded by and
20. Under the surface and above the region bounded
by and
Under the surface and above the triangle with vertices
, , and
22. Enclosed by the paraboloid and the planes ,
, ,
23. Bounded by the coordinate planes and the plane
24. Bounded by the planes , , , and
25. Enclosed by the cylinders , and the planes
,
26. Bounded by the cylinder and the planes
, in the first octant
27. Bounded by the cylinder and the planes ,
, in the first octant
28. Bounded by the cylinders and
;
29. Use a graphing calculator or computer to estimate the
-coordinates of the points of intersection of the curves
and . If is the region bounded by these curves,
estimate .
xx
D
x dA
Dy 苷 3x x
2
y 苷 x
4
x
y
2
z
2
苷 r
2
x
2
y
2
苷 r
2
z 苷 0x 苷 0
y 苷 zx
2
y
2
苷 1
z 苷 0x 苷 0
x 苷 2y,y
2
z
2
苷 4
y 苷 4z 苷 0
y 苷 x
2
z 苷 x
2
z 苷 0x y 苷 2y 苷 xz 苷 x
3x 2y z 苷 6
z 苷 0y 苷 xy 苷 1
x 苷 0z 苷 x
2
3y
2
共1, 2兲共4, 1兲共1, 1兲
z 苷 xy
21.
x 苷 y
3
x 苷 y
2
z 苷 2x y
2
y 苷 x
4
y 苷 x
x 2y z 苷 0
共0, 3兲共1, 2兲
共0, 0兲
yy
D
2xy dA, D
D
yy
D
共2x y兲 dA,
17.
1–6 Evaluate the iterated integral.
1. 2.
3. 4.
6.
7–18 Evaluate the double integral.
7.
8.
9.
10.
11.
12.
,
, is bounded by , ,
14. , is bounded by
15. ,
is the triangular region with vertices (0, 2), (1, 1),
16.
yy
D
xy
2
dA, D is enclosed by x 苷 0 and x 苷
s
1 y
2
共3, 2兲D
yy
D
y
3
dA
y 苷
s
x
and y 苷 x
2
D
yy
D
共x y兲 dA
x 苷 1y 苷 x
2
y 苷 0D
yy
D
x cos y dA
13.
D 苷 兵共x, y兲
ⱍ
0 y 1, 0 x y其
yy
D
x
s
y
2
x
2
dA
yy
D
y
2
e
xy
dA, D 苷 兵共x, y兲
ⱍ
0 y 4, 0 x y其
yy
D
x
3
dA, D 苷 兵共x, y兲
ⱍ
1 x e, 0 y ln x其
yy
D
x dA, D 苷 兵共x, y兲
ⱍ
0 x
, 0 y sin x其
yy
D
y
x
5
1
dA, D 苷 兵共x, y兲
ⱍ
0 x 1, 0 y x
2
其
yy
D
y
2
dA, D 苷 兵共x, y兲
ⱍ
1 y 1, y 2 x y其
y
1
0
y
v
0
s
1 v
2
du dv
y
兾2
0
y
cos
0
e
sin
dr d
5.
y
2
0
y
2y
y
xy dx dy
y
1
0
y
x
x
2
共1 2y兲 dy dx
y
1
0
y
2
2x
共x y兲 dy dx
y
4
0
y
s
y
0
xy
2
dx dy
EXERCISES
16.3
EXAMPLE 6 Use Property 11 to estimate the integral , where is the disk
with center the origin and radius 2.
SOLUTION Since and , we have and
therefore
Thus, using , , and in Property 11, we obtain
M
4
e
yy
D
e
sin x cos y
dA 4
e
A共D兲 苷
共2兲
2
M 苷 em 苷 e
1
苷 1兾e
e
1
e
sin x cos y
e
1
苷 e
1 sin x cos y 11 cos y 11 sin x 1
Dxx
D
e
sin x cos y
dA
SECTION 16.3 DOUBLE INTEGRALS OVER GENERAL REGIONS
||||
1009
51–52 Express as a union of regions of type I or type II and
evaluate the integral.
52.
53–54 Use Property 11 to estimate the value of the integral.
53. , is the quarter-circle with center the origin
and radius in the first quadrant
54. , is the triangle enclosed by the lines
, , and
55–56 Find the average value of over region .
55. , is the triangle with vertices ,
and
56. , is enclosed by the curves ,
, and
57. Prove Property 11.
In evaluating a double integral over a region , a sum of
iterated integrals was obtained as follows:
Sketch the region and express the double integral as an
iterated integral with reversed order of integration.
59. Evaluate , where
[Hint: Exploit the fact that
is symmetric with respect to both axes.]
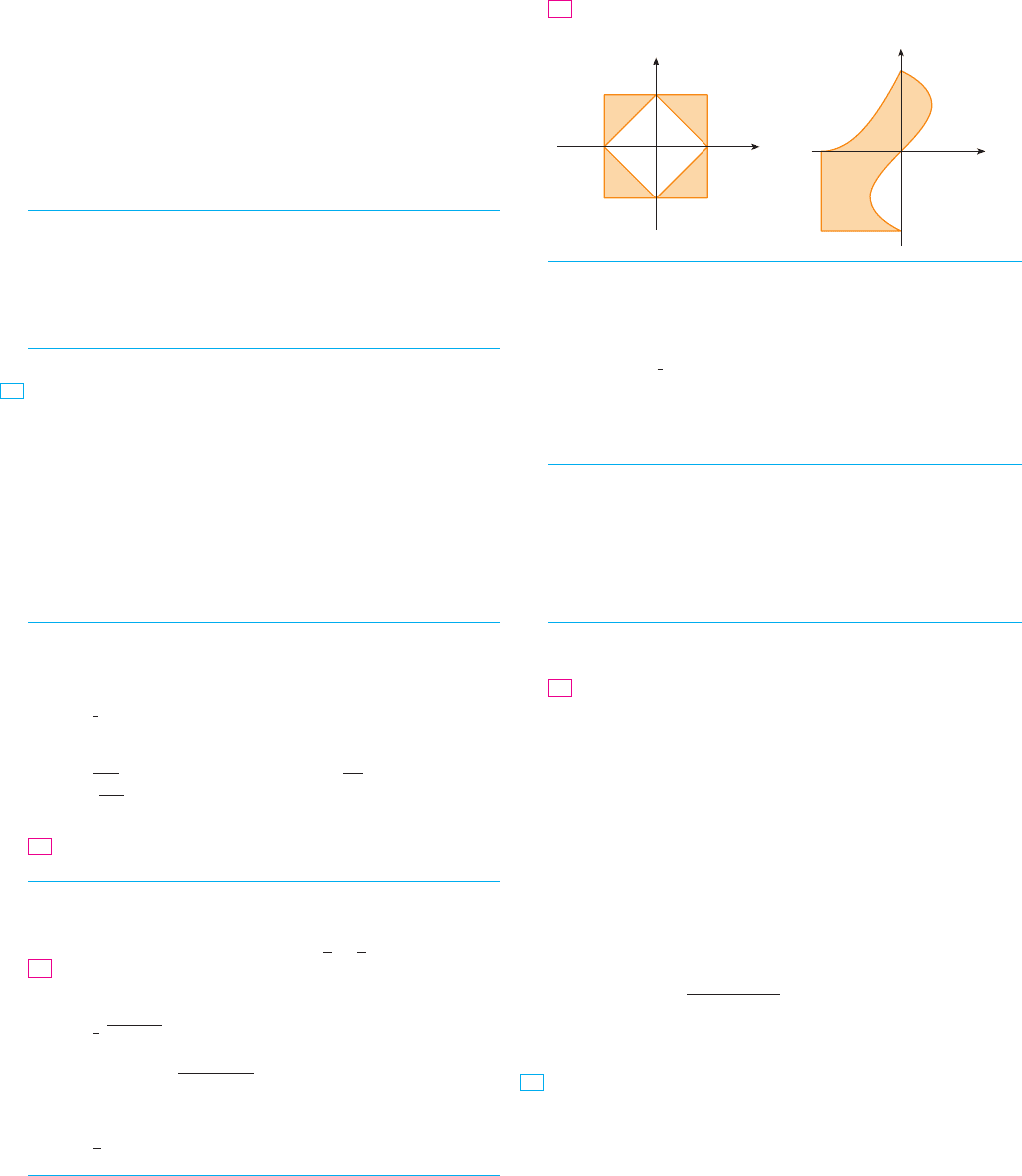
60. Use symmetry to evaluate , where
is the region bounded by the square with vertices
and .
61. Compute , where is the disk
, by first identifying the integral as the volume
of a solid.
62. Graph the solid bounded by the plane and
the paraboloid and find its exact volume.
(Use your CAS to do the graphing, to find the equations of
the boundary curves of the region of integration, and to eval-
uate the double integral.)
z 苷 4 x
2
y
2
x y z 苷 1
CAS
x
2
y
2
1
D
xx
D
s
1 x
2
y
2
dA
共0, 5兲
共5, 0兲
D
xx
D
共2 3x 4y兲 dA
D
D 苷 兵共x, y兲
ⱍ
x
2
y
2
2其.
xx
D
共x
2
tan x y
3
4兲 dA
D
yy
D
f 共x, y兲 dA 苷
y
1
0
y
2y
0
f 共x, y兲 dx dy
y
3
1
y
3y
0
f 共x, y兲 dx dy
D
58.
x 苷 1y 苷 x
2
y 苷 0Df 共x, y兲 苷 x sin y
共1, 3兲
共0, 0兲, 共1, 0兲Df 共x, y兲 苷 xy
Df
x 苷 1y 苷 2xy 苷 0
T
yy
T
sin
4
共x y兲 dA
1
2
Q
yy
Q
e
共x
2
y
2
兲
2
dA
0
_1
1
_1
x=y-Á
y=(x+1)@
y
x
0
1
_1
_1 1
D
(1,1)
x
y
yy
D
y dA
yy
D
x
2
dA
51.
D
;
30. Find the approximate volume of the solid in the first octant
that is bounded by the planes , , and and
the cylinder . (Use a graphing device to estimate
the points of intersection.)
31–32 Find the volume of the solid by subtracting two volumes.
31. The solid enclosed by the parabolic cylinders
, and the planes ,
32. The solid enclosed by the parabolic cylinder and the
planes ,
33–34 Sketch the solid whose volume is given by the iterated
integral.
33. 34.
35–38 Use a computer algebra system to find the exact volume
of the solid.
35. Under the surface and above the region
bounded by the curves and for
36. Between the paraboloids and
and inside the cylinder
37. Enclosed by
38. Enclosed by
39– 44 Sketch the region of integration and change the order of
integration.
39. 40.
41. 42.
44.
45–50 Evaluate the integral by reversing the order of integration.
46.
47. 48.
49.
50.
y
8
0
y
2
s
y
3
e
x
4
dx dy
y
1
0
y
兾2
arcsin
y
cos x
s
1 cos
2
x
dx dy
y
1
0
y
1
x
e
x兾y
dy dx
y
4
0
y
2
s
x
1
y
3
1
dy dx
y
s
0
y
s
y
cos共x
2
兲 dx dy
y
1
0
y
3
3y
e
x
2
dx dy
45.
y
1
0
y
兾4
arctan
x
f 共x, y兲 dy dx
y
2
1
y
ln
x
0
f 共x, y兲 dy dx
43.
y
3
0
y
s
9y
0
f 共x, y兲 dx dy
y
3
0
y
s
9y
2
s
9y
2
f 共x, y兲 dx dy
y
1
0
y
4
4x
f 共x, y兲 dy dx
y
4
0
y
s
x
0
f 共x, y兲 dy dx
z 苷 x
2
y
2
and z 苷 2y
z 苷 1 x
2
y
2
and z 苷 0
x
2
y
2
苷 1z 苷 8 x
2
2y
2
z 苷 2x
2
y
2
x 0y 苷 x
2
xy 苷 x
3
x
z 苷 x
3
y
4
xy
2
CAS
y
1
0
y
1x
2
0
共1 x兲 dy dx
y
1
0
y
1x
0
共1 x y兲 dy dx
z 苷 2 yz 苷 3y
y 苷 x
2
2x 2y z 10 苷 0
x y z 苷 2y 苷 x
2
1y 苷 1 x
2
y 苷 cos x
z 苷 xz 苷 0y 苷 x
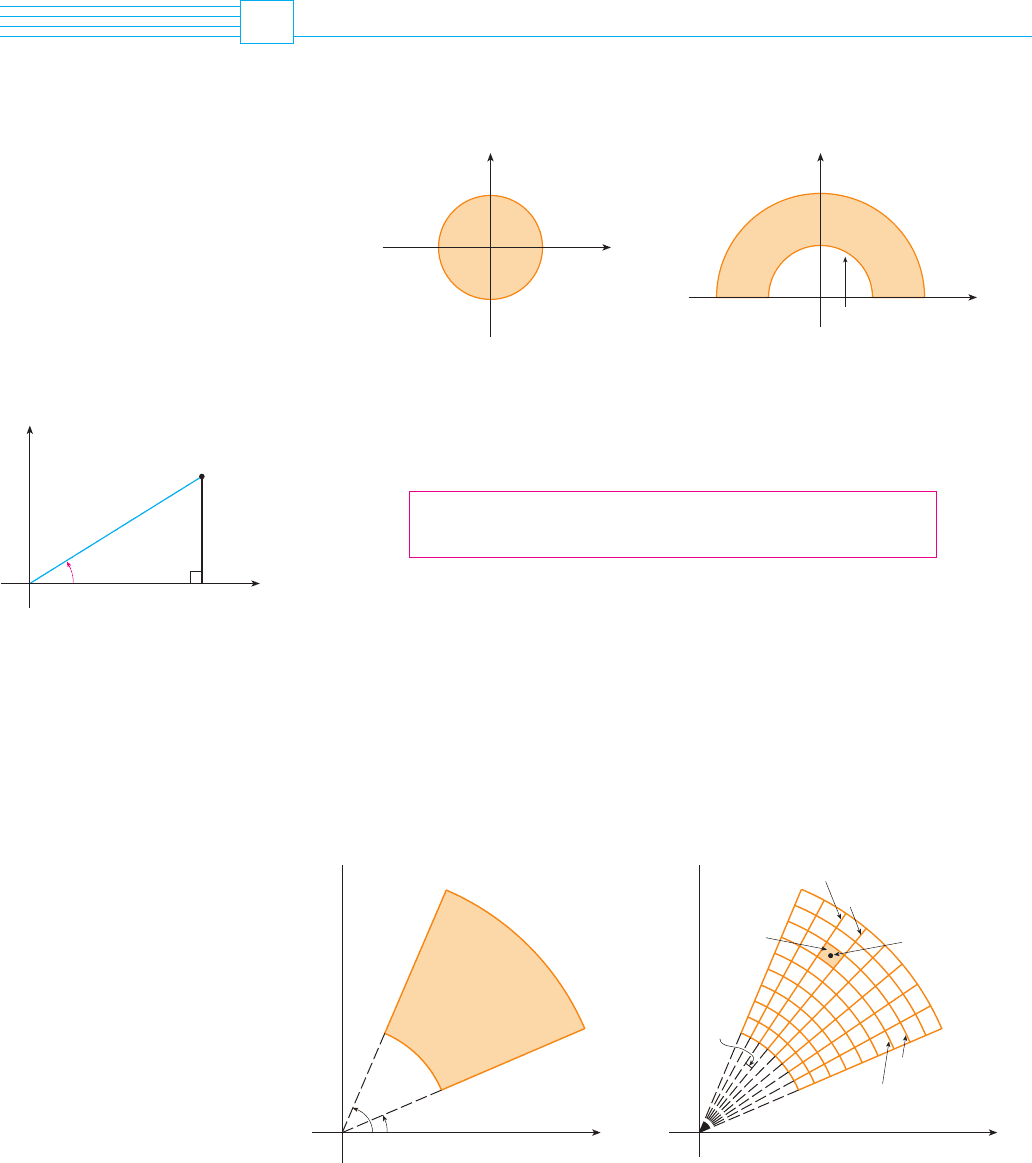
DOUBLE INTEGRALS IN POLAR COORDINATES
Suppose that we want to evaluate a double integral , where is one of the
regions shown in Figure 1. In either case the description of in terms of rectangular coor-
dinates is rather complicated but is easily described using polar coordinates.
Recall from Figure 2 that the polar coordinates of a point are related to the rect-
angular coordinates by the equations
(See Section 11.3.)
The regions in Figure 1 are special cases of a polar rectangle
which is shown in Figure 3. In order to compute the double integral , where
is a polar rectangle, we divide the interval into subintervals of equal
width and we divide the interval into subintervals of
equal width . Then the circles and the rays divide the polar
rectangle R into the small polar rectangles shown in Figure 4.
r=r
i-1
FIGURE 3 Polar rectangle FIGURE 4 Dividing R into polar subrectangles
O
∫
å
r=a
¨=å
¨=∫
r=b
R
Ψ
¨=¨
j
(r
i
*
,¨
j
*
)
r=r
i
R
ij
O
¨=¨
j-1
苷
j
r 苷 r
i
苷 共
兲兾n
关
j1
,
j
兴n关
,
兴r 苷 共b a兲兾m
关r
i1
, r
i
兴m关a, b兴R
xx
R
f 共x, y兲 dA
R 苷
兵
共r,
兲
ⱍ
a r b,
其
y 苷 r sin
x 苷 r cos
r
2
苷 x
2
y
2
共x, y兲
共r,
兲
FIGURE 1
x
0
y
R
≈+¥=1
(a) R=s(r,¨) | 0¯r¯1, 0¯¨¯2πd
x
0
y
R
≈+¥=4
≈+¥=1
(b) R=s(r,¨) | 1¯r¯2, 0¯¨¯πd
R
R
Rxx
R
f 共x, y兲 dA
16.4
1010
||||
CHAPTER 16 MULTIPLE INTEGRALS
O
y
x
¨
x
y
r
P
(r,¨)=P(x,y)
FIGURE 2
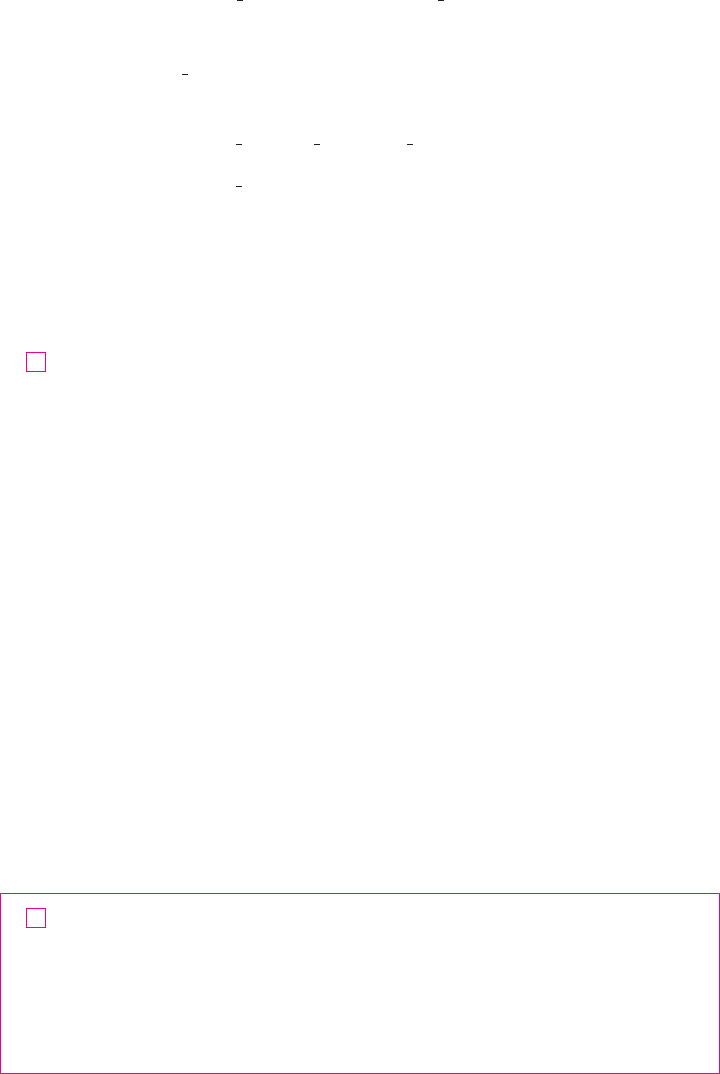
The “center” of the polar subrectangle
has polar coordinates
We compute the area of using the fact that the area of a sector of a circle with radius
and central angle is . Subtracting the areas of two such sectors, each of which has
central angle , we find that the area of is
Although we have defined the double integral in terms of ordinary rect-
angles, it can be shown that, for continuous functions , we always obtain the same
answer using polar rectangles. The rectangular coordinates of the center of are
, so a typical Riemann sum is
If we write , then the Riemann sum in Equation 1 can be writ-
ten as
which is a Riemann sum for the double integral
Therefore we have
CHANGE TO POLAR COORDINATES IN A DOUBLE INTEGRAL If is con-
tinuous on a polar rectangle given by , , where
, then
yy
R
f 共x, y兲 dA 苷
y
y
b
a
f 共r cos
, r sin
兲
r dr d
0
2
0 a r bR
f
2
苷
y
y
b
a
f 共r cos
, r sin
兲
r dr d
苷 lim
m, n
l
兺
m
i苷1
兺
n
j苷1
t共r
i
*
,
j
*
兲 r
苷
y
y
b
a
t共r,
兲
dr d
yy
R
f 共x, y兲 dA 苷 lim
m, n
l
兺
m
i苷1
兺
n
j苷1
f 共r
i
*
cos
j
*
, r
i
*
sin
j
*
兲 A
i
y
y
b
a
t共r,
兲
dr d
兺
m
i苷1
兺
n
j苷1
t共r
i
*
,
j
*
兲 r
t共r,
兲 苷 rf共r cos
, r sin
兲
兺
m
i苷1
兺
n
j苷1
f 共r
i
*
cos
j
*
, r
i
*
sin
j
*
兲 A
i
苷
兺
m
i苷1
兺
n
j苷1
f 共r
i
*
cos
j
*
, r
i
*
sin
j
*
兲 r
i
*
r
1
共r
i
*
cos
j
*
, r
i
*
sin
j
*
兲
R
ij
f
xx
R
f 共x, y兲 dA
苷
1
2
共r
i
r
i1
兲共r
i
r
i1
兲
苷 r
i
*
r
A
i
苷
1
2
r
i
2
1
2
r
i1
2
苷
1
2
共r
i
2
r
i1
2
兲
R
ij
苷
j
j1
1
2
r
2
rR
ij
j
*
苷
1
2
共
j1
j
兲r
i
*
苷
1
2
共r
i1
r
i
兲
R
ij
苷
兵
共r,
兲
ⱍ
r
i1
r r
i
,
j1
j
其
SECTION 16.4 DOUBLE INTEGRALS IN POLAR COORDINATES
||||
1011
