Stewart J. Calculus

mathematical discoveries. The details, including a translation of l’Hospital’s letter to Bernoulli

proposing the arrangement, can be found in the book by Eves [1].

Write a report on the historical and mathematical origins of l’Hospital’s Rule. Start by pro-

viding brief biographical details of both men (the dictionary edited by Gillispie [2] is a good

source) and outline the business deal between them. Then give l’Hospital’s statement of his rule,

which is found in Struik’s sourcebook [4] and more brieﬂy in the book of Katz [3]. Notice that

l’Hospital and Bernoulli formulated the rule geometrically and gave the answer in terms of dif-

ferentials. Compare their statement with the version of l’Hospital’s Rule given in Section 7.8 and

show that the two statements are essentially the same.

1. Howard Eves, In Mathematical Circles (Volume 2: Quadrants III and IV) (Boston: Prindle,

Weber and Schmidt, 1969), pp. 20–22.

2. C. C. Gillispie, ed., Dictionary of Scientiﬁc Biography (New York: Scribner’s, 1974). See the

article on Johann Bernoulli by E. A. Fellmann and J. O. Fleckenstein in Volume II and the

article on the Marquis de l’Hospital by Abraham Robinson in Volume VIII.

3. Victor Katz, A History of Mathematics: An Introduction (New York: HarperCollins, 1993),

p. 484.

4. D. J. Struik, ed., A Sourcebook in Mathematics, 1200 –1800 (Princeton, NJ: Princeton Uni-

versity Press, 1969), pp. 315–316.

482

|| ||

CHAPTER 7 INVERSE FUNCTIONS

www.stewartcalculus.com

The Internet is another source of infor-

mation for this project. Click on History

of Mathematics for a list of reliable websites.

Thomas Fisher Rare Book Library

REVIEW

C O N C E P T C H E C K

7

(d) (e) (f)

(g) (h) (i)

( j) (k) (l)

(m)

6. (a) How is the number deﬁned?

(b) Express as a limit.

(c) Why is the natural exponential function used more

often in calculus than the other exponential functions

?

(d) Why is the natural logarithmic function used more

often in calculus than the other logarithmic functions

?

7. (a) Write a differential equation that expresses the law of

natural growth.

(b) Under what circumstances is this an appropriate model for

population growth?

(c) What are the solutions of this equation?

8. (a) What does l’Hospital’s Rule say?

(b) How can you use l’Hospital’s Rule if you have a product

where and as ?

(c) How can you use l’Hospital’s Rule if you have a difference

where and as ?

(d) How can you use l’Hospital’s Rule if you have a power

where and as ?x l at!x" l 0f !x" l 0$ f !x"%

t!x"

x l at!x" l #f !x" l #f !x" " t!x"

x l at!x" l #f !x" l 0f !x"t!x"

y ! log

a

x

y ! ln x

y ! a

x

y ! e

x

e

y ! tanh

"1

x

y ! cosh

"1

xy ! sinh

"1

xy ! tanh x

y ! cosh xy ! sinh xy ! tan

"1

x

y ! cos

"1

xy ! sin

"1

xy ! log

a

x

1. (a) What is a one-to-one function? How can you tell if a func-

tion is one-to-one by looking at its graph?

(b) If is a one-to-one function, how is its inverse function

deﬁned? How do you obtain the graph of from the

graph of ?

(c) If is a one-to-one function and , write a

formula for .

2. (a) What are the domain and range of the natural exponential

function ?

(b) What are the domain and range of the natural logarithmic

function ?

(c) How are the graphs of these functions related? Sketch these

graphs by hand, using the same axes.

(d) If a is a positive number, , write an equation that

expresses in terms of .

3. (a) How is the inverse sine function deﬁned?

What are its domain and range?

(b) How is the inverse cosine function deﬁned?

What are its domain and range?

(c) How is the inverse tangent function deﬁned?

What are its domain and range? Sketch its graph.

4. Write the deﬁnitions of the hyperbolic functions , ,

and .

5. State the derivative of each function.

(a) (b) (c) y ! ln xy ! a

x

y ! e

x

tanh x

cosh xsinh x

f !x" ! tan

"1

x

f !x" ! cos

"1

x

f !x" ! sin

"1

x

ln xlog

a

x

a " 1

f !x" ! ln x

f !x" ! e

x

! f

"1

"

(

!a"

f (! f

"1

!a"" " 0f

f

"1

f

"1

f

CHAPTER 7 REVIEW

|| ||

483

Determine whether the statement is true or false. If it is true, explain why.

If it is false, explain why or give an example that disproves the statement.

1. If is one-to-one, with domain , then .

2. If is one-to-one and differentiable,with domain , then

.

3. The function , , is one-to-one.

4.

5.

If , then .

6.

7.

You can always divide by .

8. If and , then .

9. If , then .!ln x"

6

! 6 ln xx ' 0

ln!a ! b" ! ln a ! ln bb ' 0a ' 0

e

x

$

s

5

! e

s

5

ln

$

ln a

%

ln b0

%

a

%

b

tan

"1

!"1" ! 3

$

#4

"

$

#2 + x +

$

#2f !x" ! cos x

! f

"1

"(!6" ! 1#f (!6"

!f

f

"1

!f!6"" ! 6!f

10.

11.

12.

The inverse function of is .

13. 14.

15.

for all 16.

17.

18. lim

x

l

$

"

tan x

1 " cos x

!

lim

x

l

$

"

sec

2

x

sin x

! #

y

16

2

dx

x

! 3 ln 2

ln

1

10

! "

y

10

1

dx

x

xcosh x / 1

tan

"1

x !

sin

"1

x

cos

"1

x

cos

"1

x !

1

cos x

y !

1

3

ln xy ! e

3x

d

dx

!ln 10" !

1

10

d

dx

!10

x

" ! x10

x"1

T R U E - FA L S E Q U I Z

1. The graph of is shown. Is one-to-one? Explain.

2. The graph of is given.

(a) Why is one-to-one?

(b) Estimate the value of .

(c) Estimate the domain of .

(d) Sketch the graph of .

3. Suppose f is one-to-one, , and . Find

(a) and (b) .

4. Find the inverse function of .

5–9 Sketch a rough graph of the function without using a

calculator.

5. 6.

y ! "e

"x

y ! 5

x

" 1

f !x" !

x ! 1

2x ! 1

! f

"1

"(!3"f

"1

!3"

f (!7" ! 8f !7" ! 3

g

y

x0

1

t

"1

t

"1

t

"1

!2"

t

y

x0

ff

7. 8.

9.

10. Let . For large values of , which of the functions ,

, and has the largest values and which has the

smallest values?

11–12 Find the exact value of each expression.

11. (a) (b)

12. (a) (b)

13–20 Solve the equation for .

13. 14.

15. 16.

17. 18.

19. 20.

21– 47 Differentiate.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

31. 32.

y ! !arcsin 2x"

2

y !

e

1#x

x

2

y ! ln!x

2

e

x

"y ! ln!sec

2

x"

y ! e

mx

cos nxy ! e

cx

!c sin x " cos x"

y ! e

"t

!t

2

" 2t ! 2"y ! ln

)

sec 5x ! tan 5x

)

h!u" ! 10

s

u

h!

*

" ! e

tan 2

*

t!t" !

e

t

1 ! e

t

f !t" ! t

2

ln t

sin x ! 0.3tan

"1

x ! 1

log

5

!c

x

" ! dln!x ! 1" ! ln! x " 1" ! 1

ln!1 ! e

"x

" ! 3e

e

x

! 17

e

x

!

1

3

ln x !

1

3

x

tan

(

arcsin

1

2

)

ln e

$

log

10

25 ! log

10

4e

2 ln 3

y ! log

a

xy ! a

x

y ! x

a

xa ' 1

y ! 2 arctan x

y ! ln!x " 1"y ! "ln x

E X E R C I S E S

63–78 Evaluate the limit.

63. 64.

65. 66.

67. 68.

69. 70.

71. 72.

73. 74.

75. 76.

77. 78.

79– 84 Sketch the curve using the guidelines of Section 4.5.

79. 80.

81. 82.

83. 84.

;

85. Graph in a viewing rectangle that shows all the

main aspects of this function. Estimate the inﬂection points.

Then use calculus to ﬁnd them exactly.

;

86. Investigate the family of functions . What hap-

pens to the maximum and minimum points and the inﬂection

points as changes? Illustrate your conclusions by graphing

several members of the family.

87. An equation of motion of the form

represents damped oscillation of an object. Find the velocity

and acceleration of the object.

88. (a) Show that there is exactly one root of the equation

and that it lies between 2 and .

(b) Find the root of the equation in part (a) correct to four

decimal places.

89. A bacteria culture contains 200 cells initially and grows at a

rate proportional to its size. After half an hour the population

has increased to 360 cells.

(a) Find the number of bacteria after hours.

(b) Find the number of bacteria after 4 hours.

(c) Find the rate of growth after 4 hours.

(d) When will the population reach 10,000?

90. Cobalt-60 has a half-life of 5.24 years.

(a) Find the mass that remains from a 100-mg sample after

20 years.

(b) How long would it take for the mass to decay to 1 mg?

t

eln x ! 3 ! x

s ! Ae

!ct

cos!

"

t #

$

"

c

f !x" ! cxe

!cx

2

f !x" ! e

!1#x

2

y ! x # ln!x

2

# 1"y ! xe

!2x

y ! e

2x!x

2

y ! x ln x

y ! sin

!1

!1#x"y ! tan

!1

!1#x"

lim

x

l

!

%

#2"

!

!tan x"

cos x

lim

x

l

1

#

$

x

x ! 1

!

1

ln x

%

lim

x

l

0

#

x

2

ln xlim

x

l

&

x

3

e

!x

lim

x

l

&

e

4x

! 1 ! 4x

x

2

lim

x

l

0

e

4x

! 1 ! 4x

x

2

lim

x

l

0

1 ! cos x

x

2

# x

lim

x

l

0

tan

%

x

ln!1 # x"

lim

x l &

$

1 #

4

x

%

x

lim

x l &

1 # 2

x

1 ! 2

x

lim

x l &

e

!x

sin xlim

x

l

0

#

ln!sinh x"

lim

x l &

arctan!x

3

! x"lim

x

l

3

!

e

2#!x!3"

lim

x

l

10

!

ln!100 ! x

2

"lim

x

l

&

e

!3x

33. 34.

35. 36.

37. 38.

39. 40.

41. 42.

43. 44.

45. 46.

47.

48. Show that

49–52 Find in terms of .

49. 50.

51. 52.

53–54 Find .

53. 54.

55. Use mathematical induction to show that if ,

then .

56. Find if .

57–58 Find an equation of the tangent to the curve at the given

point.

57. , 58. ,

59. At what point on the curve is the tangent

horizontal?

;

60. If , ﬁnd . Graph and on the same

screen and comment.

61. (a) Find an equation of the tangent to the curve that is

parallel to the line .

(b) Find an equation of the tangent to the curve that

passes through the origin.

62. The function , where a, b, and K are

positive constants and , is used to model the concentra-

tion at time t of a drug injected into the bloodstream.

(a) Show that .

(b) Find , the rate at which the drug is cleared from

circulation.

(c) When is this rate equal to 0?

C'!t"

lim

t

l

&

C!t" ! 0

b ( a

C!t" ! K!e

!at

! e

!bt

"

y ! e

x

x ! 4y ! 1

y ! e

x

f 'ff '!x"f !x" ! xe

sin x

y ! &ln!x # 4"'

2

!e, e"y ! x ln x!0, 2"y ! !2 # x"e

!x

y ! x # arctan yy'

f

!n"

!x" ! !x # n"e

x

f !x" ! xe

x

f !x" ! ln!2x"f !x" ! 2

x

f

!n"

!x"

f !x" ! t!ln x"f !x" ! ln

(

t!x"

(

f !x" ! t!e

x

"f !x" ! e

t!x"

t'f '

d

dx

$

1

2

tan

!1

x #

1

4

ln

!x # 1"

2

x

2

# 1

%

!

1

!1 # x"!1 # x

2

"

y ! cos

(

e

s

tan 3x

)

y ! x tanh

!1

s

x

y ! cosh

!1

!sinh x"

y !

!x

2

# 1"

4

!2x # 1"

3

!3x ! 1"

5

y ! ln!cosh 3x"

xe

y

! y ! 1y ! ln

$

1

x

%

#

1

ln x

y ! arctan

(

arcsin

s

x

)

y ! ln sin x !

1

2

sin

2

x

y ! !cos x"

x

y ! x sinh!x

2

"

F!z" ! log

10

!1 # z

2

"H!v" ! v tan

!1

v

y ! e

cos x

# cos!e

x

"y ! 3

x ln x

484

|| ||

CHAPTER 7 INVERSE FUNCTIONS

116. What is the area of the largest rectangle in the ﬁrst quadrant

with two sides on the axes and one vertex on the curve

?

117. What is the area of the largest triangle in the ﬁrst quadrant

with two sides on the axes and the third side tangent to the

curve ?

118. Evaluate without using the Fundamental Theorem of

Calculus. [Hint: Use the deﬁnition of a deﬁnite integral with

right endpoints, sum a geometric series, and then use

l’Hospital’s Rule.]

119. If , where , then, by the Fundamental

Theorem,

Use l’Hospital’s Rule to show that is continuous at .

120. Show that

121. If is a continuous function such that

for all , ﬁnd an explicit formula for .

122. (a) Show that for .

(b) Show that, for , ,

(c) Deduce Napier’s Inequality:

if .

(d) Give a geometric proof of Napier’s Inequality by com-

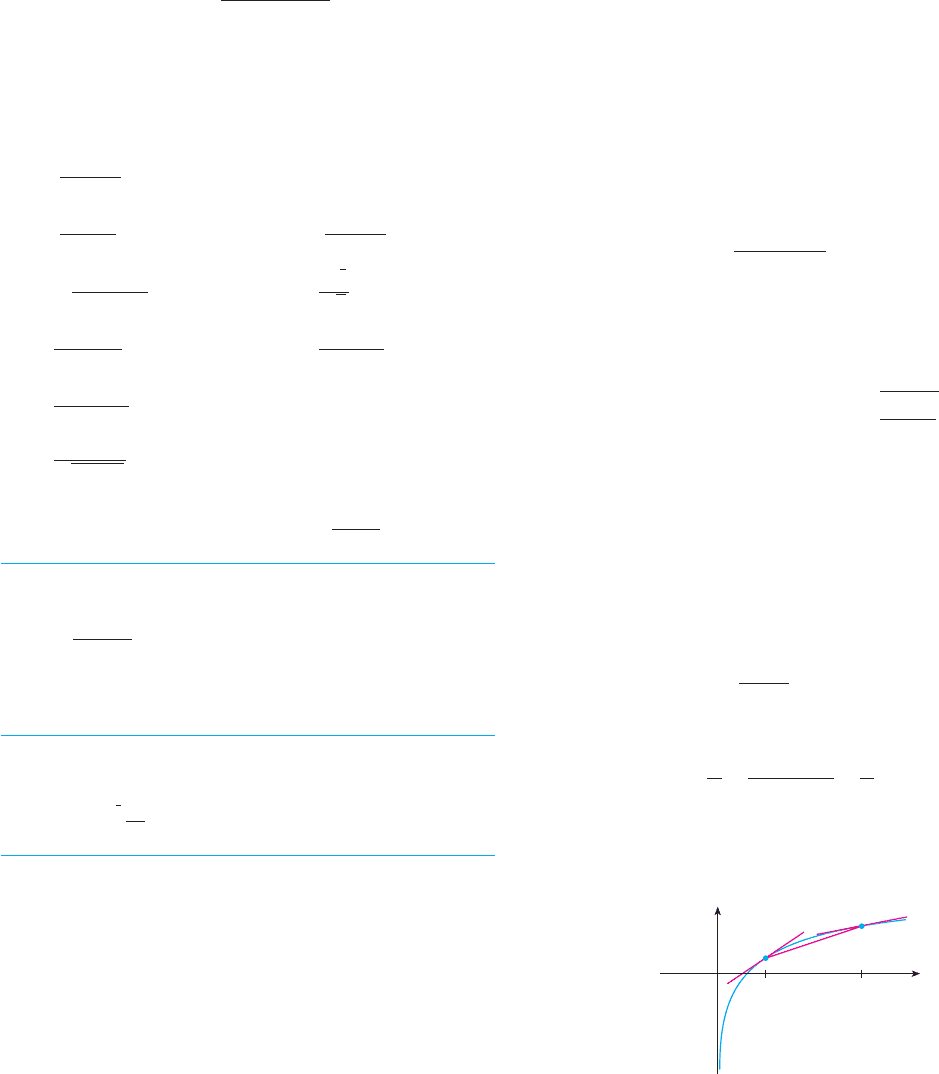
paring the slopes of the three lines shown in the ﬁgure.

(e) Give another proof of Napier’s Inequality by applying

Property 8 of integrals (see Section 5.2) to .

x

b

a

!1#x" dx

0

x

y

a

b

y=lnx

b ( a ( 0

1

b

)

ln b ! ln a

b ! a

)

1

a

x ! 1

x

)

ln x

x " 1x ( 0

x ( 0, x " 1ln x

)

x ! 1

f !x"x

y

x

0

f !t" dt ! xe

2x

#

y

x

0

e

!t

f!t" dt

f

cos)arctan&sin!arccot x"'* !

+

x

2

# 1

x

2

# 2

!1F

F!!1" ! ln b ! ln a

x " !1 F!x" !

b

x#1

! a

x#1

x # 1

a, b ( 0F!x" ! x

b

a

t

x

dt

x

1

0

e

x

dx

y ! e

!x

y ! e

!x

91. The biologist G. F. Gause conducted an experiment in the

1930s with the protozoan Paramecium and used the population

function

to model his data, where was measured in days. Use this

model to determine when the population was increasing most

rapidly.

92–105 Evaluate the integral.

92. 93.

94. 95.

96. 97.

98. 99.

100. 101.

102. 103.

104. 105.

106–108 Use properties of integrals to prove the inequality.

106.

107. 108.

109–110 Find .

109. 110.

111. Find the average value of the function on the

interval .

112. Find the area of the region bounded by the curves

, and .

113. Find the volume of the solid obtained by rotating about the

-axis the region under the curve from

to .

114. If , ﬁnd .

115. If , ﬁnd . ! f

!1

"

'

!

%

#4"f !x" ! ln x # tan

!1

x

! f

!1

"

'

!1"f !x" ! x # x

2

# e

x

x ! 1

x ! 0y ! 1#!1 # x

4

"y

x ! 1y ! e

x

, y ! e

!x

, x ! !2

&1, 4'

f !x" ! 1#x

f !x" !

y

2x

ln

x

e

!t

2

dtf !x" !

y

s

x

1

e

s

ds

f '!x"

y

1

0

x sin

!1

x dx *

%

#4

y

1

0

e

x

cos x dx * e ! 1

y

1

0

s

1 # e

2x

dx + e ! 1

y

$

1 ! x

x

%

2

dx

y

sinh au du

y

2

tan

,

sec

2

,

d

,

y

x

s

1 ! x

4

dx

y

tan x ln!cos x" dx

y

csc

2

x

1 # cot x

dx

y

x # 1

x

2

# 2x

dx

y

cos!ln x"

x

dx

y

e

s

x

s

x

dx

y

%

#2

0

cos x

1 # sin

2

x

dx

y

1

0

e

x

1 # e

2x

dx

y

5

2

dr

1 # 2r

y

1

0

ye

!2y

2

dy

y

4

0

1

16 # t

2

dt

t

P!t" !

64

1 # 31e

!0.7944t

CHAPTER 7 REVIEW

|| ||

485

486

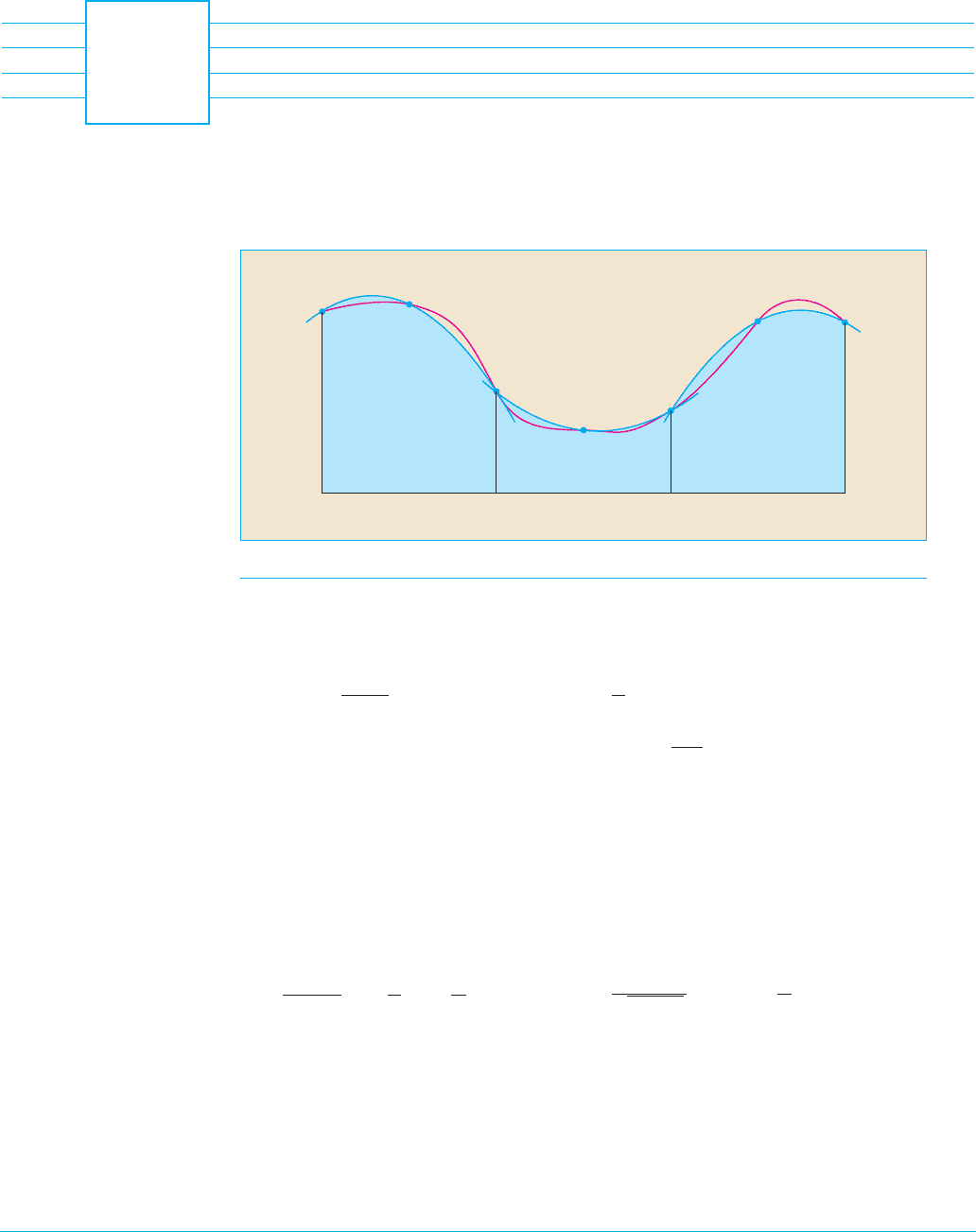
EXAMPLE 1 For what values of does the equation have exactly one

solution?

SOLUTION One of the most important principles of problem solving is to draw a diagram,

even if the problem as stated doesn’t explicitly mention a geometric situation. Our pres-

ent problem can be reformulated geometrically as follows: For what values of does the

curve intersect the curve in exactly one point?

Let’s start by graphing and for various values of . We know that,

for , is a parabola that opens upward if and downward if .

Figure 1 shows the parabolas for several positive values of . Most of them

don’t intersect at all and one intersects twice. We have the feeling that there

must be a value of (somewhere between and ) for which the curves intersect

exactly once, as in Figure 2.

To ﬁnd that particular value of , we let be the -coordinate of the single point of

intersection. In other words, , so is the unique solution of the given equa-

tion. We see from Figure 2 that the curves just touch, so they have a common tangent

line when . That means the curves and have the same slope when

. Therefore

Solving the equations and , we get

Thus and

For negative values of we have the situation illustrated in Figure 3: All parabolas

with negative values of intersect exactly once. And let’s not forget

about : The curve is just the -axis, which intersects exactly

once.

To summarize, the required values of are and . M

c * 0c ! 1#!2e"c

y

y=lnx

x

0

F I G U R E 3

y ! ln xxy ! 0x

2

! 0c ! 0

y ! ln xcy ! cx

2

c

c !

ln a

a

2

!

ln e

1#2

e

!

1

2e

a ! e

1#2

ln a ! ca

2

! c !

1

2c

!

1

2

1#a ! 2caln a ! ca

2

1

a

! 2ca

x ! a

y ! cx

2

y ! ln xx ! a

aln a ! ca

2

xac

0.30.1c

y ! ln x

cy ! cx

2

c

)

0c ( 0y ! cx

2

c " 0

cy ! cx

2

y ! ln x

y ! cx

2

y ! ln x

c

ln x ! cx

2

c

P R O B L E M S P L U S

N Cover up the solution to the example and try

it yourself.

0

3≈

≈

0.3≈

0.1≈

y=lnx

≈

1

2

x

y

F I G U R E 1

y=lnx

y=c≈

c=?

y

x

0

a

F I G U R E 2

487

1. If a rectangle has its base on the -axis and two vertices on the curve , show that the

rectangle has the largest possible area when the two vertices are at the points of inﬂection of

the curve.

2. Prove that is an irrational number.

3. Show that

where and are positive numbers, , and .

4. Show that .

5. Show that, for ,

6. Suppose is continuous, , , , and . Find the value of

the integral .

7. Show that is one-to-one and ﬁnd .

8. If

show that .

9. For what value of is the following equation true?

10. Sketch the set of all points such that .

11. Prove that for all .

12. Show that, for all positive values of and ,

13. For what value of does the equation have exactly one solution?

14. For which positive numbers is it true that for all ?

15. For which positive numbers does the curve intersect the line ?

16. For what values of does the curve have inﬂection points?y ! cx

3

# e

x

c

y ! xy ! a

x

a

xa

x

+ 1 # xa

e

2x

! k

s

x

k

e

x#y

xy

+ e

2

yx

xcosh!sinh x"

)

sinh!cosh x"

(

x # y

(

* e

x

!x, y"

lim

x

l

&

$

x # a

x ! a

%

x

! e

a

y' !

1

a # cos x

y !

x

s

a

2

! 1

!

2

s

a

2

! 1

arctan

sin x

a #

s

a

2

! 1 # cos x

! f

!1

"'!0"f !x" ! x

x

1

s

1 # t

3

dt

x

1

0

f

!1

!y" dy

x

1

0

f !x" dx !

1

3

f '!x" ( 0f !1" ! 1f !0" ! 0f

x

1 # x

2

)

tan

!1

x

)

x

x ( 0

sin

!1

!tanh x" ! tan

!1

!sinh x"

,

! tan

!1

!b#a"r

2

! a

2

# b

2

ba

d

n

dx

n

!e

ax

sin bx" ! r

n

e

ax

sin!bx # n

,

"

log

2

5

y ! e

!x

2

x

PROBLEM S

P R O B L E M S P L U S

488

Because of the Fundamental Theorem of Calculus, we can integrate a function if we know

an antiderivative, that is, an indeﬁnite integral. We summarize here the most important

integrals that we have learned so far.

In this chapter we develop techniques for using these basic integration formulas to obtain

indeﬁnite integrals of more complicated functions. We learned the most important method of

integration, the Substitution Rule, in Section 5.5. The other general technique, integration by

parts, is presented in Section 8.1. Then we learn methods that are special to particular classes

of functions, such as trigonometric functions and rational functions.

Integration is not as straightforward as differentiation; there are no rules that absolutely

guarantee obtaining an indeﬁnite integral of a function. Therefore we discuss a strategy for

integration in Section 8.5.

y

1

s

a

2

! x

2

dx ! sin

!1

!

x

a

"

" C

y

1

x

2

" a

2

dx !

1

a

tan

!1

!

x

a

"

" C

y

cot x dx ! ln

#

sin x

#

" C

y

tan x dx ! ln

#

sec x

#

" C

y

cosh x dx ! sinh x " C

y

sinh x dx ! cosh x " C

y

csc x cot x dx ! !csc x " C

y

sec x tan x dx ! sec x " C

y

csc

2

x dx ! !cot x " C

y

sec

2

x dx ! tan x " C

y

cos x dx ! sin x " C

y

sin x dx ! !cos x " C

y

a

x

dx !

a

x

ln a

" C

y

e

x

dx ! e

x

" C

y

1

x

dx ! ln

#

x

#

" C

$n " !1%

y

x

n

dx !

x

n"1

n " 1

" C

Simpson’s Rule estimates

integrals by approximating

graphs with parabolas.

TECHNIQUES OF

INTEGRATION

8

INTEGRATION BY PARTS

Every differentiation rule has a corresponding integration rule. For instance, the Substi-

tution Rule for integration corresponds to the Chain Rule for differentiation. The rule that

corresponds to the Product Rule for differentiation is called the rule for integration by

parts.

The Product Rule states that if and are differentiable functions, then

In the notation for indeﬁnite integrals this equation becomes

or

We can rearrange this equation as

Formula 1 is called the formula for integration by parts. It is perhaps easier to remem-

ber in the following notation. Let and . Then the differentials are

and , so, by the Substitution Rule, the formula for integration

by parts becomes

EXAMPLE 1 Find .

SOLUTION USING FORMULA 1 Suppose we choose and . Then

and . (For we can choose any antiderivative of .) Thus, using Formula

1, we have

It’s wise to check the answer by differentiating it. If we do so, we get , as

expected.

x sin x

! !x cos x " sin x " C

! !x cos x "

y

cos x dx

! x $!cos x% !

y

$!cos x% dx

y

x sin x dx ! f $x%t$x% !

y

t$x%f #$x% dx

t#tt$x% ! !cos x

f #$x% ! 1t#$x% ! sin xf $x% ! x

y

x sin x dx

y

u dv ! uv !

y

v du

2

dv ! t#$x% dxdu ! f #$x% dx

v ! t$x%u ! f $x%

y

f $x%t#$x% dx ! f $x%t$x% !

y

t$x%f #$x% dx

1

y

f $x%t#$x% dx "

y

t$x%f #$x% dx ! f $x%t$x%

y

& f $x%t#$x% " t$x%f #$x%' dx ! f $x%t$x%

d

dx

& f $x%t$x%' ! f $x%t#$x% " t$x%f #$x%

tf

8.1

489

SOLUTION USING FORMULA 2 Let

Then

and so

M

Our aim in using integration by parts is to obtain a simpler integral than the one

we started with. Thus in Example 1 we started with and expressed it in terms

of the simpler integral . If we had instead chosen and , then

and , so integration by parts gives

Although this is true, is a more difﬁcult integral than the one we started with.

In general, when deciding on a choice for and , we usually try to choose to

be a function that becomes simpler when differentiated (or at least not more complicated)

as long as can be readily integrated to give .

EXAMPLE 2 Evaluate .

SOLUTION Here we don’t have much choice for and . Let

Then

Integrating by parts, we get

Integration by parts is effective in this example because the derivative of the function

is simpler than .

M

ff $x% ! ln x

! x ln x ! x " C

! x ln x !

y

dx

y

ln x dx ! x ln x !

y

x

dx

x

du !

1

x

dx

v ! x

u ! ln x d

v ! dx

dvu

y

ln x dx

V

vdv ! t#$x% dx

u ! f $x%dvu

x x

2

cos x dx

y

x sin x dx ! $sin x%

x

2

!

1

2

y

x

2

cos x dx

v ! x

2

(2du ! cos x dx

dv ! x dxu ! sin xx cos x dx

x x sin x dx

NOTE

! !x cos x " sin x " C

! !x cos x "

y

cos x dx

y

x sin x dx !

y

x sin x dx ! x $!cos x% !

y

$!cos x% dx

v ! !cos x du ! dx

dv ! sin x dx u ! x

490

|| ||

CHAPTER 8 TECHNIQUES OF INTEGRATION

u d√ u √ √ du

N It is helpful to use the pattern:

v ! ! du ! !

dv ! ! u ! !

N It’s customary to write as .

x dxx 1 dx

N Check the answer by differentiating it.

EXAMPLE 3 Find .

SOLUTION Notice that becomes simpler when differentiated (whereas is unchanged

when differentiated or integrated), so we choose

Then

Integration by parts gives

The integral that we obtained, , is simpler than the original integral but is still not

obvious. Therefore, we use integration by parts a second time, this time with and

. Then , , and

Putting this in Equation 3, we get

M

EXAMPLE 4 Evaluate .

SOLUTION Neither nor becomes simpler when differentiated, but we try choosing

and anyway. Then and , so integration by

parts gives

The integral that we have obtained, , is no simpler than the original one, but

at least it’s no more difﬁcult. Having had success in the preceding example integrating

by parts twice, we persevere and integrate by parts again. This time we use and

. Then , , and

At ﬁrst glance, it appears as if we have accomplished nothing because we have arrived at

, which is where we started. However, if we put the expression for

from Equation 5 into Equation 4 we get

y

e

x

sin x dx ! !e

x

cos x " e

x

sin x !

y

e

x

sin x dx

x e

x

cos x dxx e

x

sin x dx

y

e

x

cos x dx ! e

x

sin x !

y

e

x

sin x dx

5

v ! sin xdu ! e

x

dxdv ! cos x dx

u ! e

x

x e

x

cos x dx

y

e

x

sin x dx ! !e

x

cos x "

y

e

x

cos x dx

4

v ! !cos xdu ! e

x

dxdv ! sin x dxu ! e

x

sin xe

x

y

e

x

sin x dx

V

where C

1

! !2C ! t

2

e

t

! 2te

t

" 2e

t

" C

1

! t

2

e

t

! 2$te

t

! e

t

" C%

y

t

2

e

t

dt ! t

2

e

t

! 2

y

te

t

dt

! te

t

! e

t

" C

y

te

t

dt ! te

t

!

y

e

t

dt

v ! e

t

du ! dtdv ! e

t

dt

u ! t

x te

t

dt

y

t

2

e

t

dt ! t

2

e

t

! 2

y

te

t

dt

3

du ! 2t dt v ! e

t

u ! t

2

dv ! e

t

dt

e

t

2

y

t

2

e

t

dt

V

SECTION 8.1 INTEGRATION BY PARTS

|| ||

491

N An easier method, using complex numbers, is

given in Exercise 50 in Appendix G.

Stewart J. Calculus

Подождите немного. Документ загружается.