Stewart J. Calculus

EXAMPLE 1 Determine whether the series converges or diverges.

SOLUTION For large the dominant term in the denominator is so we compare the

given series with the series . Observe that

because the left side has a bigger denominator. (In the notation of the Comparison Test,

is the left side and is the right side.) We know that

is convergent because it’s a constant times a -series with . Therefore

is convergent by part (i) of the Comparison Test. M

Although the condition or in the Comparison Test is given for

all , we need verify only that it holds for , where is some ﬁxed integer, because

the convergence of a series is not affected by a ﬁnite number of terms. This is illustrated

in the next example.

EXAMPLE 2 Test the series for convergence or divergence.

SOLUTION This series was tested (using the Integral Test) in Example 4 in Section 12.3,

but it is also possible to test it by comparing it with the harmonic series. Observe that

for and so

We know that is divergent ( -series with ). Thus the given series is divergent

by the Comparison Test.

M

The terms of the series being tested must be smaller than those of a convergent

series or larger than those of a divergent series. If the terms are larger than the terms of a

convergent series or smaller than those of a divergent series, then the Comparison Test

doesn’t apply. Consider, for instance, the series

The inequality

is useless as far as the Comparison Test is concerned because is convergent

and . Nonetheless, we have the feeling that ought to be convergent

because it is very similar to the convergent geometric series . In such cases the fol-

lowing test can be used.

$

(

1

2

)

n

$

1+(2

n

" 1)a

n

$ b

n

$

b

n

!

$

(

1

2

)

n

1

2

n

" 1

$

1

2

n

!

n!1

1

2

n

" 1

NOTE 2

p ! 1p

$

1+n

n ) 3

ln n

n

$

1

n

n ) 3ln n $ 1

!

n!1

ln n

n

V

Nn ) Nn

a

n

) b

n

a

n

' b

n

NOTE 1

!

n!1

5

2n

2

# 4n # 3

p ! 2 $ 1p

!

n!1

5

2n

2

!

5

2

!

n!1

1

n

2

b

n

a

n

5

2n

2

# 4n # 3

*

5

2n

2

$

5+(2n

2

)

2n

2

n

!

n!1

5

2n

2

# 4n # 3

V

742

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

THE LIMIT COMPARISON TEST Suppose that and are series with positive

terms. If

where c is a ﬁnite number and , then either both series converge or both

diverge.

PROOF Let m and M be positive numbers such that . Because is close

to c for large n, there is an integer N such that

and so

If converges, so does . Thus converges by part (i) of the Comparison

Test. If diverges, so does and part (ii) of the Comparison Test shows that

diverges. M

EXAMPLE 3 Test the series for convergence or divergence.

SOLUTION We use the Limit Comparison Test with

and obtain

Since this limit exists and is a convergent geometric series, the given series con-

verges by the Limit Comparison Test. M

EXAMPLE 4 Determine whether the series converges or diverges.

SOLUTION The dominant part of the numerator is and the dominant part of the denomi-

nator is . This suggests taking

! lim

n

l

!

2 #

3

n

2

.

5

n

5

# 1

!

2 # 0

2

s

0 # 1

! 1

lim

n

l

!

a

n

b

n

! lim

n

l

!

2n

2

# 3n

s

5 # n

5

!

n

1+2

2

! lim

n

l

!

2n

5+2

# 3n

3+2

2

s

5 # n

5

b

n

!

2n

2

n

5+2

!

2

n

1+2

a

n

!

2n

2

# 3n

s

5 # n

5

s

n

5

! n

5+2

2n

2

!

n!1

2n

2

# 3n

s

5 # n

5

$

1+2

n

lim

n

l

!

a

n

b

n

! lim

n

l

!

1+(2

n

" 1)

1+2

n

! lim

n

l

!

2

n

2

n

" 1

! lim

n

l

!

1

1 " 1+2

n

! 1 $ 0

b

n

!

1

2

n

a

n

!

1

2

n

" 1

!

n!1

1

2

n

" 1

$

a

n

$

mb

n

$

b

n

$

a

n

$

Mb

n

$

b

n

mb

n

*

a

n

*

Mb

n

when n $ N

m

*

a

n

b

n

*

M when n $ N

a

n

+b

n

m

*

c

*

M

c $ 0

lim

n

l

!

a

n

b

n

! c

$

b

n

$

a

n

SECTION 12.4 THE COMPARISON TESTS

|| ||

743

N Exercises 40 and 41 deal with the

cases and .c ! !c ! 0

Since is divergent

(

-series with

)

, the given series diverges

by the Limit Comparison Test. M

Notice that in testing many series we ﬁnd a suitable comparison series by keeping

only the highest powers in the numerator and denominator.

ESTIMATING SUMS

If we have used the Comparison Test to show that a series converges by comparison

with a series , then we may be able to estimate the sum by comparing remainders.

As in Section 12.3, we consider the remainder

For the comparison series we consider the corresponding remainder

Since for all , we have . If is a -series, we can estimate its remain-

der as in Section 12.3. If is a geometric series, then is the sum of a geometric

series and we can sum it exactly (see Exercises 35 and 36). In either case we know that

is smaller than .

EXAMPLE 5 Use the sum of the ﬁrst 100 terms to approximate the sum of the series

. Estimate the error involved in this approximation.

SOLUTION Since

the given series is convergent by the Comparison Test. The remainder for the compari-

son series was estimated in Example 5 in Section 12.3 using the Remainder Esti-

mate for the Integral Test. There we found that

Therefore the remainder for the given series satisﬁes

With we have

Using a programmable calculator or a computer, we ﬁnd that

with error less than .

M

0.00005

!

n!1

1

n

3

# 1

,

!

100

n!1

1

n

3

# 1

, 0.6864538

R

100

'

1

2(100)

2

! 0.00005

n ! 100

R

n

' T

n

'

1

2n

2

R

n

T

n

'

y

!

n

1

x

3

dx !

1

2n

2

$

1+n

3

T

n

1

n

3

# 1

*

1

n

3

$

1+(n

3

# 1)

V

T

n

R

n

T

n

$

b

n

T

n

p

$

b

n

R

n

' T

n

na

n

' b

n

T

n

! t " t

n

! b

n#1

# b

n#2

# & & &

$

b

n

R

n

! s " s

n

! a

n#1

# a

n#2

# & & &

$

a

n

$

b

n

$

a

n

$

b

n

p !

1

2

*

1p

$

b

n

! 2

$

1+n

1+2

744

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

33 –36 Use the sum of the ﬁrst 10 terms to approximate the sum of

the series. Estimate the error.

33. 34.

35. 36.

The meaning of the decimal representation of a number

(where the digit is one of the numbers 0, 1,

2, . . . , 9) is that

Show that this series always converges.

38. For what values of does the series converge?

39. Prove that if and converges, then also

converges.

40. (a) Suppose that and are series with positive terms

and is convergent. Prove that if

then is also convergent.

(b) Use part (a) to show that the series converges.

(i)

(ii)

(a) Suppose that and are series with positive terms

and is divergent. Prove that if

then is also divergent.

(b) Use part (a) to show that the series diverges.

(i)

(ii)

42. Give an example of a pair of series and with positive

terms where and diverges, but

converges. (Compare with Exercise 40.)

43. Show that if and then is

divergent.

44. Show that if and is convergent, then

is convergent.

45. If is a convergent series with positive terms, is it true that

is also convergent?

46. If and are both convergent series with positive terms,

is it true that is also convergent?

$

a

n

b

n

$

b

n

$

a

n

$

sin(a

n

)

$

a

n

$

ln(1 # a

n

)

$

a

n

a

n

$ 0

$

a

n

lim

n l !

na

n

" 0, a

n

$ 0

$

a

n

$

b

n

lim

n l !

(a

n

+b

n

) ! 0

$

b

n

$

a

n

!

n!1

ln n

n

!

n!2

1

ln n

$

a

n

lim

n l !

a

n

b

n

! !

$

b

n

$

b

n

$

a

n

41.

!

n!1

ln n

s

n

e

n

!

n!1

ln n

n

3

$

a

n

lim

n l !

a

n

b

n

! 0

$

b

n

$

b

n

$

a

n

$

a

n

2

$

a

n

a

n

) 0

$

!

n!2

1+(n

p

ln n)p

0.d

1

d

2

d

3

d

4

. . . !

d

1

10

#

d

2

10

2

#

d

3

10

3

#

d

4

10

4

# & & &

d

i

0.d

1

d

2

d

3

. . .

37.

!

n!1

n

(n # 1)3

n

!

n!1

1

1 # 2

n

!

n!1

sin

2

n

3

!

n!1

1

s

n

4

# 1

Suppose and are series with positive terms and is

known to be convergent.

(a) If for all , what can you say about ? Why?

(b) If for all , what can you say about ? Why?

2. Suppose and are series with positive terms and is

known to be divergent.

(a) If for all n, what can you say about ? Why?

(b) If for all n, what can you say about ? Why?

3–32 Determine whether the series converges or diverges.

3. 4.

5. 6.

7.

9.

11. 12.

13. 14.

15. 16.

18.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

32.

!

n!1

1

n

1#1+n

!

n!1

sin

"

1

n

#

31.

!

n!1

n!

n

!

n!1

1

n!

!

n!1

e

1+n

n

!

n!1

"

1 #

1

n

#

2

e

"n

!

n!1

n # 5

s

3

n

7

# n

2

!

n!1

1 # n # n

2

s

1 # n

2

# n

6

!

n!1

n

2

" 5n

n

3

# n # 1

!

n!1

5 # 2n

(1 # n

2

)

2

!

n!3

n # 2

(n # 1)

3

!

n!1

s

n # 2

2n

2

# n # 1

!

n!1

n # 4

n

n # 6

n

!

n!1

1 # 4

n

1 # 3

n

!

n!1

1

2n # 3

!

n!1

1

s

n

2

# 1

17.

!

n!1

1

s

n

3

# 1

!

n!1

2 # ("1)

n

s

n

!

n!2

s

n

n " 1

!

n!1

arctan n

n

1.2

!

n! 0

1 # sin n

10

n

!

n!1

n " 1

n4

n

!

n!1

n

2

" 1

3n

4

# 1

10.

!

n!1

cos

2

n

2

# 1

!

n!1

4 # 3

n

2

n

8.

!

n!1

9

n

3 # 10

n

!

n!1

n " 1

n

2

s

n

!

n!1

n # 1

n

s

n

!

n!2

n

3

n

4

" 1

!

n!1

n

2n

3

# 1

$

a

n

a

n

*

b

n

$

a

n

a

n

$ b

n

$

b

n

$

b

n

$

a

n

$

a

n

na

n

*

b

n

$

a

n

na

n

$ b

n

$

b

n

$

b

n

$

a

n

1.

E X E R C I S E S

12.4

SECTION 12.4 THE COMPARISON TESTS

|| ||

745

ALTERNATING SERIES

The convergence tests that we have looked at so far apply only to series with positive

terms. In this section and the next we learn how to deal with series whose terms are not

necessarily positive. Of particular importance are alternating series, whose terms alternate

in sign.

An alternating series is a series whose terms are alternately positive and negative. Here

are two examples:

We see from these examples that the th term of an alternating series is of the form

where is a positive number.

(

In fact, .

)

The following test says that if the terms of an alternating series decrease toward 0 in

absolute value, then the series converges.

THE ALTERNATING SERIES TEST If the alternating series

satisﬁes

(i)

(ii)

then the series is convergent.

Before giving the proof let’s look at Figure 1, which gives a picture of the idea behind

the proof. We ﬁrst plot on a number line. To ﬁnd we subtract , so is to the

left of . Then to ﬁnd we add , so is to the right of . But, since , is to

the left of . Continuing in this manner, we see that the partial sums oscillate back and

forth. Since , the successive steps are becoming smaller and smaller. The even par-

tial sums , , , . . . are increasing and the odd partial sums , , , . . . are decreasing.

Thus it seems plausible that both are converging to some number , which is the sum of

the series. Therefore we consider the even and odd partial sums separately in the follow-

ing proof.

F I G U R E 1

0 s¡

s™ s£s¢ s∞sß

s

b¡

-b™

+b£

-b¢

+b∞

-bß

s

5

s

3

s

1

s

6

s

4

s

2

b

n

l 0

s

1

s

3

b

3

*

b

2

s

2

s

3

b

3

s

3

s

1

s

2

b

2

s

2

s

1

! b

1

lim

n l !

b

n

! 0

for all nb

n#1

' b

n

b

n

$ 0

!

n!1

("1)

n"1

b

n

! b

1

" b

2

# b

3

" b

4

# b

5

" b

6

# & & &

b

n

!

-

a

n

-

b

n

a

n

! ("1)

n

b

n

ora

n

! ("1)

n"1

b

n

"

1

2

#

2

3

"

3

4

#

4

5

"

5

6

#

6

7

" & & & !

!

n!1

("1)

n

n # 1

1 "

1

2

#

1

3

"

1

4

#

1

5

"

1

6

# & & & !

!

n!1

("1)

n"1

n

12.5

746

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

PROOF OF THE ALTERNATING SERIES TEST We ﬁrst consider the even partial sums:

In general

Thus

But we can also write

Every term in brackets is positive, so for all . Therefore the sequence

of even partial sums is increasing and bounded above. It is therefore convergent by the

Monotonic Sequence Theorem. Let’s call its limit , that is,

Now we compute the limit of the odd partial sums:

[by condition (ii)]

Since both the even and odd partial sums converge to , we have

[see Exercise 80(a) in Section 12.1] and so the series is convergent.

M

EXAMPLE 1 The alternating harmonic series

satisﬁes

(i) because

(ii)

so the series is convergent by the Alternating Series Test.

M

EXAMPLE 2 The series is alternating but

lim

n

l

!

b

n

! lim

n

l

!

3n

4n " 1

! lim

n

l

!

3

4 "

1

n

!

3

4

!

n!1

("1)

n

3n

4n " 1

V

lim

n l !

b

n

! lim

n l !

1

n

! 0

1

n # 1

*

1

n

b

n#1

*

b

n

1 "

1

2

#

1

3

"

1

4

# & & & !

!

n!1

("1)

n"1

n

V

lim

n l !

s

n

! ss

! s

! s # 0

! lim

n l !

s

2n

# lim

n l !

b

2n#1

lim

n l !

s

2n#1

! lim

n l !

(s

2n

# b

2n#1

)

lim

n l !

s

2n

! s

s

%s

2n

&ns

2n

' b

1

s

2n

! b

1

" (b

2

" b

3

) " (b

4

" b

5

) " & & & " (b

2n"2

" b

2n"1

) " b

2n

0 ' s

2

' s

4

' s

6

' & & & ' s

2n

' & & &

since b

2n

' b

2n"1

s

2n

! s

2n"2

# (b

2n"1

" b

2n

) ) s

2n"2

since b

4

' b

3

s

4

! s

2

# (b

3

" b

4

) ) s

2

since b

2

' b

1

s

2

! b

1

" b

2

) 0

SECTION 12.5 ALTERNATING SERIES

|| ||

747

F I G U R E 2

0

n

1

%a

n

&

%s

n

&

N Figure 2 illustrates Example 1 by showing the

graphs of the terms and the

partial sums . Notice how the values of

zigzag across the limiting value, which appears

to be about . In fact, it can be proved that

the exact sum of the series is

(see Exercise 36).

ln 2 , 0.693

0.7

s

n

s

n

a

n

! ("1)

n"1

+n

so condition (ii) is not satisﬁed. Instead, we look at the limit of the nth term of the series:

This limit does not exist, so the series diverges by the Test for Divergence.

M

EXAMPLE 3 Test the series for convergence or divergence.

SOLUTION The given series is alternating so we try to verify conditions (i) and (ii) of the

Alternating Series Test.

Unlike the situation in Example 1, it is not obvious that the sequence given by

is decreasing. However, if we consider the related function

, we ﬁnd that

Since we are considering only positive , we see that if , that is,

. Thus is decreasing on the interval

.

This means that

and therefore when . (The inequality can be veriﬁed directly but

all that really matters is that the sequence is eventually decreasing.)

Condition (ii) is readily veriﬁed:

Thus the given series is convergent by the Alternating Series Test.

M

ESTIMATING SUMS

A partial sum of any convergent series can be used as an approximation to the total sum

, but this is not of much use unless we can estimate the accuracy of the approximation. The

error involved in using is the remainder . The next theorem says that

for series that satisfy the conditions of the Alternating Series Test, the size of the error is

smaller than , which is the absolute value of the ﬁrst neglected term.

ALTERNATING SERIES ESTIMATION THEOREM If is the sum of an

alternating series that satisﬁes

(i) and (ii)

then

PROOF We know from the proof of the Alternating Series Test that s lies between any two

consecutive partial sums and . It follows that

M

-

s " s

n

-

'

-

s

n#1

" s

n

-

! b

n#1

s

n#1

s

n

-

R

n

-

!

-

s " s

n

-

' b

n#1

lim

n l !

b

n

! 00 ' b

n#1

' b

n

s !

$

("1)

n"1

b

n

b

n#1

R

n

! s " s

n

s , s

n

s

n

lim

n

l

!

b

n

! lim

n

l

!

n

2

n

3

# 1

! lim

n

l

!

1

n

1 #

1

n

3

! 0

%b

n

&

b

2

*

b

1

n ) 2b

n#1

*

b

n

f (n # 1)

*

f (n)

(

s

3

2

, !

)

fx $

s

3

2

2 " x

3

*

0f +(x)

*

0x

f +(x) !

x(2 " x

3

)

(x

3

# 1)

2

f (x) ! x

2

+(x

3

# 1)

b

n

! n

2

+(n

3

# 1)

!

n!1

("1)

n#1

n

2

n

3

# 1

lim

n

l

!

a

n

! lim

n

l

!

("1)

n

3n

4n " 1

748

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

N Instead of verifying condition (i) of the Alter-

nating Series Test by computing a derivative,

we could verify that directly by using

the technique of Solution 1 of Example 12 in

Section 12.1.

b

n#1

*

b

n

N You can see geometrically why the

Alternating Series Estimation Theorem is true

by looking at Figure 1 (on page 746). Notice that

and so on. Notice

also that lies between any two consecutive

partial sums.

s

-

s " s

5

-

*

b

6

,s " s

4

*

b

5

,

EXAMPLE 4 Find the sum of the series correct to three decimal places.

(By deﬁnition, .)

SOLUTION We ﬁrst observe that the series is convergent by the Alternating Series Test

because

(i)

(ii) so as

To get a feel for how many terms we need to use in our approximation, let’s write out

the ﬁrst few terms of the series:

Notice that

and

By the Alternating Series Estimation Theorem we know that

This error of less than does not affect the third decimal place, so we have

correct to three decimal places. M

|

The rule that the error (in using to approximate ) is smaller than the ﬁrst

neglected term is, in general, valid only for alternating series that satisfy the conditions

of the Alternating Series Estimation Theorem. The rule does not apply to other types of

series.

ss

n

NOTE

s , 0.368

0.0002

-

s " s

6

-

' b

7

*

0.0002

s

6

! 1 " 1 #

1

2

"

1

6

#

1

24

"

1

120

#

1

720

, 0.368056

b

7

!

1

5040

*

1

5000

! 0.0002

! 1 " 1 #

1

2

"

1

6

#

1

24

"

1

120

#

1

720

"

1

5040

# & & &

s !

1

0!

"

1

1!

#

1

2!

"

1

3!

#

1

4!

"

1

5!

#

1

6!

"

1

7!

# & & &

n l !

1

n!

l 00

*

1

n!

*

1

n

l 0

1

(n # 1)!

!

1

n! (n # 1)

*

1

n!

0! ! 1

!

n!0

("1)

n

n!

V

SECTION 12.5 ALTERNATING SERIES

|| ||

749

N In Section 12.10 we will prove that

for all , so what we have

obtained in Example 4 is actually an approxi-

mation to the number .e

"1

xe

x

!

$

!

n!0

x

n

+n!

9. 10.

12.

14.

15. 16.

18.

19. 20.

!

n!1

"

n

5

#

n

!

n!1

("1)

n

n!

!

n!1

("1)

n

cos

"

,

n

#

!

n!1

("1)

n

sin

"

,

n

#

17.

!

n!1

sin(n

,

+2)

n!

!

n!1

cos n

,

n

3+4

!

n!1

("1)

n"1

ln n

n

!

n!2

("1)

n

ln n

13.

!

n!1

("1)

n"1

e

1+n

n

!

n!1

("1)

n#1

n

2

n

3

# 4

11.

!

n!1

("1)

n

s

n

1 # 2

s

n

!

n!1

("1)

n

10

n

1. (a) What is an alternating series?

(b) Under what conditions does an alternating series converge?

(c) If these conditions are satisﬁed, what can you say about the

remainder after terms?

2–20 Test the series for convergence or divergence.

2.

4.

5. 6.

8.

!

n!1

("1)

n

s

n

3

# 2

!

n!1

("1)

n

3n " 1

2n # 1

7.

!

n!1

("1)

n"1

ln(n # 4)

!

n!1

("1)

n"1

2n # 1

1

s

2

"

1

s

3

#

1

s

4

"

1

s

5

#

1

s

6

" & & &

4

7

"

4

8

#

4

9

"

4

10

#

4

11

" & & &

3.

"

1

3

#

2

4

"

3

5

#

4

6

"

5

7

# & & &

n

E X E R C I S E S

12.5

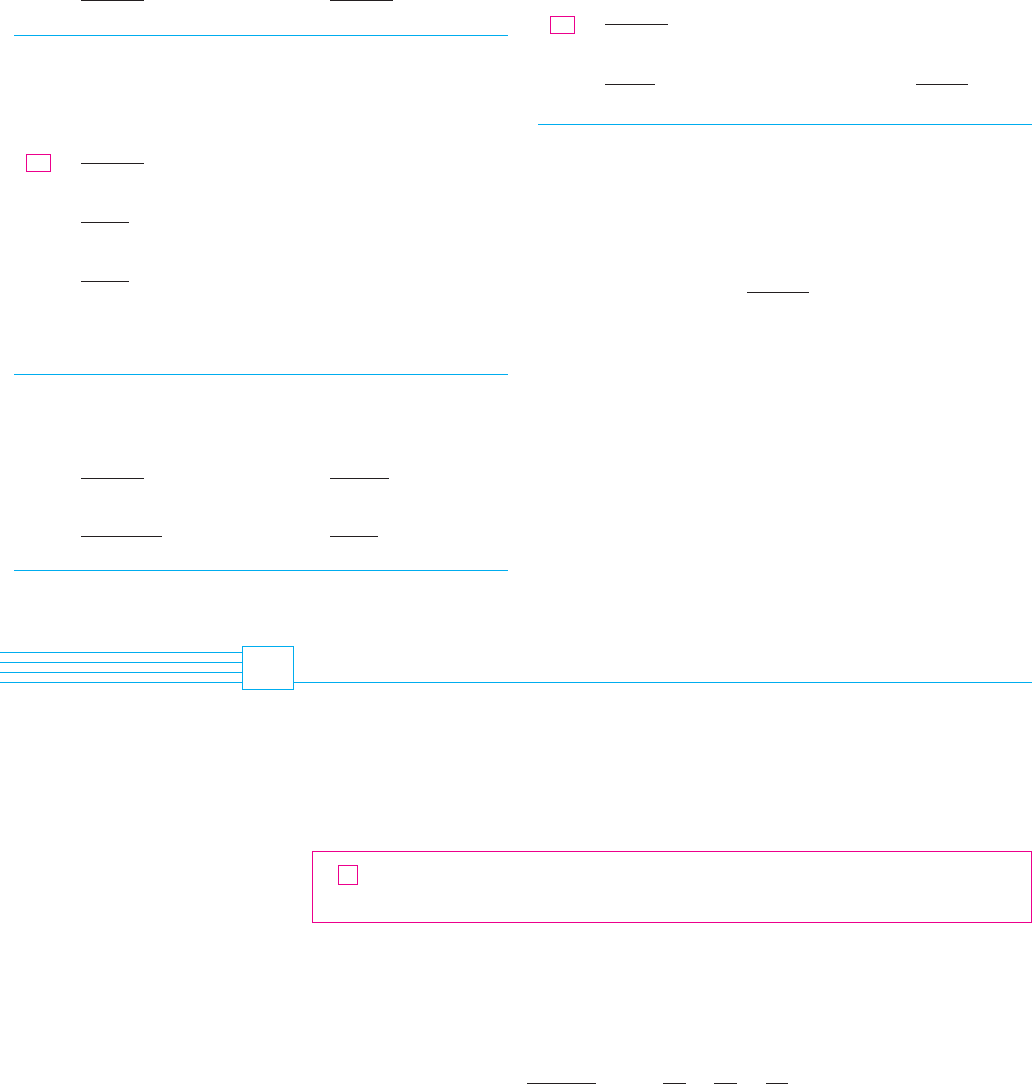
31. Is the 50th partial sum of the alternating series

an overestimate or an underestimate of the

total sum? Explain.

32–34 For what values of is each series convergent?

33. 34.

35. Show that the series , where if is odd

and if is even, is divergent. Why does the Alter-

nating Series Test not apply?

36. Use the following steps to show that

Let and be the partial sums of the harmonic and alter-

nating harmonic series.

(a) Show that .

(b) From Exercise 40 in Section 12.3 we have

as

and therefore

as

Use these facts together with part (a) to show that

as .n l !s

2n

l ln 2

n l !h

2n

" ln!2n" l

#

n l !h

n

" ln n l

#

s

2n

! h

2n

" h

n

s

n

h

n

#

!

n!1

!"1"

n"1

n

! ln 2

nb

n

! 1$n

2

nb

n

! 1$n

%

!"1"

n"1

b

n

#

!

n!2

!"1"

n"1

!ln n"

p

n

#

!

n!1

!"1"

n

n $ p

#

!

n!1

!"1"

n"1

n

p

32.

p

%

!

n!1

!"1"

n"1

$n

s

50

;

21–22 Calculate the ﬁrst 10 partial sums of the series and graph

both the sequence of terms and the sequence of partial sums on

the same screen. Estimate the error in using the 10th partial sum

to approximate the total sum.

21. 22.

23–26 Show that the series is convergent. How many terms of

the series do we need to add in order to ﬁnd the sum to the indi-

cated accuracy?

24.

25.

26.

27–30 Approximate the sum of the series correct to four

decimal places.

27. 28.

29. 30.

#

!

n!1

!"1"

n

3

n

n!

#

!

n!1

!"1"

n"1

n

2

10

n

#

!

n!1

!"1"

n

8

n

#

!

n!1

!"1"

n$1

n

5

(

&

error

&

%

0.01

)

#

!

n!1

!"1"

n"1

ne

"n

(

&

error

&

%

0.000005

)

#

!

n!0

!"1"

n

10

n

n!

(

&

error

&

%

0.0001

)

#

!

n!1

!"1"

n

n 5

n

(

&

error

&

%

0.00005

)

#

!

n!1

!"1"

n$1

n

6

23.

#

!

n!1

!"1"

n"1

n

3

#

!

n!1

!"1"

n"1

n

3$2

750

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

ABSOLUTE CONVERGENCE AND THE RATIO AND ROOT TESTS

Given any series , we can consider the corresponding series

whose terms are the absolute values of the terms of the original series.

DEFINITION A series is called absolutely convergent if the series of

absolute values is convergent.

Notice that if is a series with positive terms, then and so absolute con-

vergence is the same as convergence in this case.

EXAMPLE 1 The series

#

!

n!1

!"1"

n"1

n

2

! 1 "

1

2

$

1

3

2

"

1

4

2

$ & & &

&

a

n

&

! a

n

%

a

n

%

&

a

n

&

%

a

n

1

#

!

n!1

&

a

n

&

!

&

a

1

&

$

&

a

2

&

$

&

a

3

&

$ & & &

%

a

n

12.6

N We have convergence tests for series with

positive terms and for alternating series. But

what if the signs of the terms switch back and

forth irregularly? We will see in Example 3 that

the idea of absolute convergence sometimes

helps in such cases.

is absolutely convergent because

is a convergent -series ( ).

M

EXAMPLE 2 We know that the alternating harmonic series

is convergent (see Example 1 in Section 12.5), but it is not absolutely convergent

because the corresponding series of absolute values is

which is the harmonic series ( -series with ) and is therefore divergent.

M

DEFINITION A series is called conditionally convergent if it is conver-

gent but not absolutely convergent.

Example 2 shows that the alternating harmonic series is conditionally convergent. Thus

it is possible for a series to be convergent but not absolutely convergent. However, the next

theorem shows that absolute convergence implies convergence.

THEOREM If a series is absolutely convergent, then it is convergent.

PROOF Observe that the inequality

is true because is either or . If is absolutely convergent, then is

convergent, so is convergent. Therefore, by the Comparison Test,

is convergent. Then

is the difference of two convergent series and is therefore convergent.

M

EXAMPLE 3 Determine whether the series

is convergent or divergent.

SOLUTION This series has both positive and negative terms, but it is not alternating.

(The ﬁrst term is positive, the next three are negative, and the following three are posi-

tive: The signs change irregularly.) We can apply the Comparison Test to the series of

absolute values

#

!

n!1

'

cos n

n

2

'

!

#

!

n!1

&

cos n

&

n

2

#

!

n!1

cos n

n

2

!

cos 1

1

2

$

cos 2

2

$

cos 3

3

2

$ & & &

V

#

a

n

!

#

(

a

n

$

&

a

n

&

)

"

#

&

a

n

&

%

(

a

n

$

&

a

n

&

)

%

2

&

a

n

&

%

&

a

n

&

%

a

n

"a

n

a

n

&

a

n

&

0 ' a

n

$

&

a

n

&

' 2

&

a

n

&

%

a

n

3

%

a

n

2

p ! 1p

#

!

n!1

'

!"1"

n"1

n

'

!

#

!

n!1

1

n

! 1 $

1

2

$

1

3

$

1

4

$ & & &

#

!

n!1

!"1"

n"1

n

! 1 "

1

2

$

1

3

"

1

4

$ & & &

p ! 2p

#

!

n!1

'

!"1"

n"1

n

2

'

!

#

!

n!1

1

n

2

! 1 $

1

2

$

1

3

2

$

1

4

2

$ & & &

SECTION 12.6 ABSOLUTE CONVERGENCE AND THE RATIO AND ROOT TESTS

|| ||

751

F I G U R E 1

0

n

0.5

(a

n

)

(s

n

)

N Figure 1 shows the graphs of the terms and

partial sums of the series in Example 3. Notice

that the series is not alternating but has positive

and negative terms.

s

n

a

n

Stewart J. Calculus

Подождите немного. Документ загружается.