Stewart J. Calculus

Подождите немного. Документ загружается.

782

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

17. , 18. ,

19. , 20. ,

21. Prove that the series obtained in Exercise 7 represents

for all .

22. Prove that the series obtained in Exercise 18 represents

for all .

23. Prove that the series obtained in Exercise 11 represents

for all .

24. Prove that the series obtained in Exercise 12 represents

for all .

25–28 Use the binomial series to expand the function as a power

series. State the radius of convergence.

25. 26.

28.

29–38 Use a Maclaurin series in Table 1 to obtain the Maclaurin

series for the given function.

29. 30.

31. 32.

34.

36.

37.

Hint: Use

38.

;

39 – 42 Find the Maclaurin series of (by any method) and its

radius of convergence. Graph and its ﬁrst few Taylor polynomials

on the same screen. What do you notice about the relationship

between these polynomials and ?

40.

41. 42.

43. Use the Maclaurin series for to calculate correct to ﬁve

decimal places.

#0.2

f &x' ! ln&1 ! x

'f &x' ! xe

f &x' ! e

! cos xf &x' ! cos&x

39.

f &x' !

x # sin x

if x " 0

if x ! 0

sin

x !

&1 # cos 2x'.

][

f &x' ! sin

f &x' !

2 ! x

f &x' !

4 ! x

35.

f &x' ! x

tan

'f &x' ! x cos

(

)

33.

f &x' ! e

! 2e

f &x' ! e

! e

f &x' ! cos&

x,2'f &x' ! sin

&1 # x'

2,3

&2 ! x'

27.

&1 ! x'

1 ! x

cosh x

sinh x

sin x

sin

a ! 1f &x' ! x

a ! 9f &x' ! 1,

a !

,2f &x' ! sin xa !

f &x' ! cos x

1. If for all , write a formula for .

2. The graph of is shown.

(a) Explain why the series

is not the Taylor series of centered at 1.

(b) Explain why the series

is not the Taylor series of centered at 2.

3. If for ﬁnd the Maclaurin

series for and its radius of convergence.

4. Find the Taylor series for centered at 4 if

What is the radius of convergence of the Taylor series?

5–12 Find the Maclaurin series for using the deﬁnition

of a Maclaurin series. [Assume that has a power series expan-

sion. Do not show that .] Also ﬁnd the associated radius

of convergence.

7. 8.

9. 10.

11. 12.

13–20 Find the Taylor series for centered at the given value

of . [Assume that has a power series expansion. Do not show

that .]

13. ,

14. ,

16. , a ! #3f &x' ! 1,xa ! 3f &x' ! e

15.

a ! #2f &x' ! x # x

a ! 1f &x' ! x

# 3x

! 1

&x' l 0

f &x'

f &x' ! cosh xf &x' ! sinh x

f &x' ! xe

f &x' ! e

f &x' ! cos 3xf &x' ! sin

f &x' ! ln&1 ! x'f &x' ! &1 # x'

&x' l 0

f &x'

&n'

&4' !

&#1'

&n ! 1'

n ! 0, 1, 2, . . . ,f

&n'

&0' ! &n ! 1'!

2.8 ! 0.5&x # 2' ! 1.5&x # 2'

# 0.1&x # 2'

! " " "

1.6 # 0.8&x # 1' ! 0.4&x # 1'

# 0.1&x # 1'

! " " "

0 x

xf &x' !

n!0

&x # 5'

E X E R C I S E S

12.10

SECTION 12.10 TAYLOR AND MACLAURIN SERIES

|| ||

783

61. 62.

63–68 Find the sum of the series.

64.

65. 66.

67.

68.

69. Prove Taylor’s Inequality for , that is, prove that if

for , then

70. (a) Show that the function deﬁned by

is not equal to its Maclaurin series.

;

(b) Graph the function in part (a) and comment on its behavior

near the origin.

71. Use the following steps to prove (17).

(a) Let . Differentiate this series to show that

(b) Let and show that .

72. In Exercise 53 in Section 11.2 it was shown that the length of

the ellipse , , where , is

where is the eccentricity of the ellipse.

Expand the integrand as a binomial series and use the result of

Exercise 46 in Section 8.1 to express as a series in powers of

the eccentricity up to the term in .e

e !

# b

L ! 4a

1 # e

sin

(

a ) b ) 0y ! b cos

(

x ! a sin

(

t&x' ! &1 ! x'

h*&x' ! 0h&x' ! &1 ! x'

t&x'

1t*&x' !

kt&x'

1 ! x

(

)

t&x' !

n!0

f &x' !

#1,x

if x " 0

if x ! 0

)

&x'

)

x # a

)

for

)

x # a

)

+ d

)

x # a

)

+ d

)

f ,&x'

)

+ M

n ! 2

1 # ln 2 !

&ln 2'

! " " "

3 !

! " " "

(

n!0

(

n!0

&#1'

2n!1

&2n ! 1'!

(

n!0

&#1'

&2n'!

(

n!0

&#1'

63.

y ! e

ln&1 # x'y !

sin x

44. Use the Maclaurin series for to compute correct to

ﬁve decimal places.

(a) Use the binomial series to expand .

(b) Use part (a) to ﬁnd the Maclaurin series for .

46. (a) Expand as a power series.

(b) Use part (a) to estimate correct to three decimal

places.

47–50 Evaluate the indeﬁnite integral as an inﬁnite series.

47. 48.

49. 50.

51–54 Use series to approximate the deﬁnite integral to within the

indicated accuracy.

51. (three decimal places)

52. (ﬁve decimal places)

53.

54.

55–57 Use series to evaluate the limit.

55. 56.

58. Use the series in Example 12(b) to evaluate

We found this limit in Example 4 in Section 7.8 using l’Hospi-

tal’s Rule three times. Which method do you prefer?

59–62 Use multiplication or division of power series to ﬁnd the

ﬁrst three nonzero terms in the Maclaurin series for the function.

60.

y ! sec xy ! e

cos x

59.

lim

tan x # x

lim

sin x # x !

57.

lim

1 # cos x

1 ! x # e

lim

x # tan

(

)

error

)

0.001

)

0.5

(

)

error

)

5 & 10

)

0.4

1 ! x

0.2

-tan

' ! sin&x

'. dx

x cos&x

arctan&x

' dx

cos x # 1

# 1

x cos&x

' dx

1.1

1 ! x

sin

1 # x

45.

sin 3-sin x

The Binomial Theorem, which gives the expansion of , was known to Chinese mathe-

maticians many centuries before the time of Newton for the case where the exponent k is a

positive integer. In 1665, when he was 22, Newton was the ﬁrst to discover the inﬁnite series

expansion of when k is a fractional exponent (positive or negative). He didn’t publish

his discovery, but he stated it and gave examples of how to use it in a letter (now called the

epistola prior) dated June 13, 1676, that he sent to Henry Oldenburg, secretary of the Royal

Society of London, to transmit to Leibniz. When Leibniz replied, he asked how Newton had

discovered the binomial series. Newton wrote a second letter, the epistola posterior of Octo-

ber 24, 1676, in which he explained in great detail how he arrived at his discovery by a very

indirect route. He was investigating the areas under the curves from 0 to x for

, 1, 2, 3, 4, . . . . These are easy to calculate if n is even. By observing patterns and inter-

polating, Newton was able to guess the answers for odd values of n. Then he realized he could

get the same answers by expressing as an inﬁnite series.

Write a report on Newton’s discovery of the binomial series. Start by giving the statement of

the binomial series in Newton’s notation (see the epistola prior on page 285 of [4] or page 402

of [2]). Explain why Newton’s version is equivalent to Theorem 17 on page 778. Then read

Newton’s epistola posterior (page 287 in [4] or page 404 in [2]) and explain the patterns that

Newton discovered in the areas under the curves . Show how he was able to

guess the areas under the remaining curves and how he veriﬁed his answers. Finally, explain how

these discoveries led to the binomial series. The books by Edwards [1] and Katz [3] contain

commentaries on Newton’s letters.

1. C. H. Edwards, The Historical Development of the Calculus (New York: Springer-Verlag,

1979), pp. 178–187.

2. John Fauvel and Jeremy Gray, eds., The History of Mathematics: A Reader (London:

MacMillan Press, 1987).

3. Victor Katz, A History of Mathematics: An Introduction (New York: HarperCollins, 1993),

pp. 463–466.

4. D. J. Struik, ed., A Sourcebook in Mathematics, 1200–1800 (Princeton, NJ: Princeton

University Press, 1969).

y ! &1 # x

n,2

&1 # x

n,2

n ! 0

y ! &1 # x

n,2

&a ! b'

HOW NEWTON DISCOVERED THE BINOMIAL SERIES

W R I T I N G

P R O J E C T

784

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

This project deals with the function

1. Use your computer algebra system to evaluate for and .

Does it appear that has a limit as ?

2. Use the CAS to graph near . Does it appear that has a limit as ?

3. Try to evaluate with l’Hospital’s Rule, using the CAS to ﬁnd derivatives of the

numerator and denominator. What do you discover? How many applications of l’Hospital’s

Rule are required?

4. Evaluate by using the CAS to ﬁnd sufﬁciently many terms in the Taylor series

of the numerator and denominator. (Use the command

taylor in Maple or Series in

Mathematica.)

5. Use the limit command on your CAS to ﬁnd directly. (Most computer algebra

systems use the method of Problem 4 to compute limits.)

In view of the answers to Problems 4 and 5, how do you explain the results of Problems 1 and 2?

lim

f &x'

lim

f &x'

lim

f &x'

x l 0fx ! 0f

x l 0f

0.0001x ! 1, 0.1, 0.01, 0.001,f &x'

f &x' !

sin&tan x' # tan&sin x'

arcsin&arctan x' # arctan&arcsin x'

AN ELUSIVE LIMIT

CAS

L A B O R A T O R Y

P R O J E C T

APPLICATIONS OF TAYLOR POLYNOMIALS

In this section we explore two types of applications of Taylor polynomials. First we look

at how they are used to approximate functions––computer scientists like them because

polynomials are the simplest of functions. Then we investigate how physicists and engi-

neers use them in such ﬁelds as relativity, optics, blackbody radiation, electric dipoles, the

velocity of water waves, and building highways across a desert.

APPROXIMATING FUNCTIONS BY POLYNOMIALS

Suppose that is equal to the sum of its Taylor series at a:

In Section 12.10 we introduced the notation for the th partial sum of this series

and called it the th-degree Taylor polynomial of at . Thus

Since is the sum of its Taylor series, we know that as and so can

be used as an approximation to : .

Notice that the ﬁrst-degree Taylor polynomial

is the same as the linearization of f at a that we discussed in Section 3.9. Notice also that

and its derivative have the same values at a that and have. In general, it can be

shown that the derivatives of at agree with those of up to and including derivatives

of order (see Exercise 38).

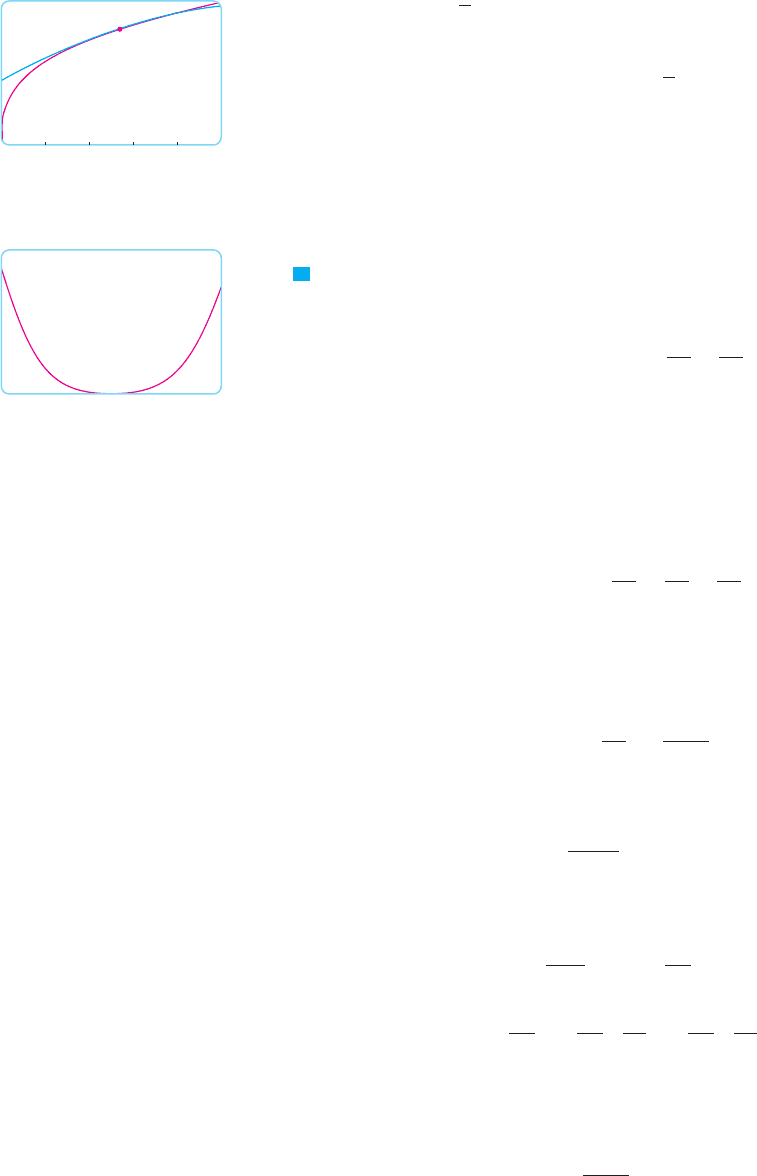
To illustrate these ideas let’s take another look at the graphs of and its ﬁrst few

Taylor polynomials, as shown in Figure 1. The graph of is the tangent line to

at ; this tangent line is the best linear approximation to near . The graph

of is the parabola , and the graph of is the cubic curve

, which is a closer ﬁt to the exponential curve than .

The next Taylor polynomial would be an even better approximation, and so on.

The values in the table give a numerical demonstration of the convergence of the Taylor

polynomials to the function . We see that when the convergence is

very rapid, but when it is somewhat slower. In fact, the farther is from 0, the more

slowly converges to .

When using a Taylor polynomial to approximate a function , we have to ask the

questions: How good an approximation is it? How large should we take to be in order to

achieve a desired accuracy? To answer these questions we need to look at the absolute

value of the remainder:

)

&x'

)

f &x' # T

&x'

)

&x'

xx ! 3

x ! 0.2y ! e

&x'

y ! e

y ! 1 ! x ! x

,2 ! x

y ! 1 ! x ! x

,2T

&0, 1'e

&0, 1'

y ! e

faT

f *fT

&x' ! f &a' ! f *&a'&x # a'

f &x' # T

&x'f

n l %T

&x' l f &x'f

! f &a' !

f *&a'

&x # a' !

f .&a'

&x # a'

! " " " !

&n'

&a'

&x # a'

&x' !

(

i!0

&i'

&a'

&x # a'

afn

&x'

f &x' !

(

n!0

&n'

&a'

&x # a'

f &x'

12.11

SECTION 12.11 APPLICATIONS OF TAYLOR POLYNOMIALS

|| ||

785

1.220000 8.500000

1.221400 16.375000

1.221403 19.412500

1.221403 20.009152

1.221403 20.079665

1.221403 20.085537e

&x'

x ! 3.0x ! 0.2

y=´

y=T£(x)

(0,1)

y=T™(x)

y=T¡(x)

F I G U R E 1

There are three possible methods for estimating the size of the error:

1. If a graphing device is available, we can use it to graph and thereby esti-

mate the error.

2. If the series happens to be an alternating series, we can use the Alternating Series

Estimation Theorem.

3. In all cases we can use Taylor’s Inequality (Theorem 12.10.9), which says that if

, then

EXAMPLE 1

(a) Approximate the function by a Taylor polynomial of degree 2 at .

(b) How accurate is this approximation when ?

SOLUTION

(a)

Thus the second-degree Taylor polynomial is

The desired approximation is

(b) The Taylor series is not alternating when , so we can’t use the Alternating

Series Estimation Theorem in this example. But we can use Taylor’s Inequality with

and :

where . Because , we have and so

Therefore we can take . Also , so and

. Then Taylor’s Inequality gives

Thus, if , the approximation in part (a) is accurate to within .

0.00047 + x + 9

)

&x'

)

0.0021

! 1

0.0021

0.0004

)

x # 8

)

+ 1

#1 + x # 8 + 17 + x + 9M ! 0.0021

f ,&x' !

8,3

0.0021

8,3

/ 7

8,3

x / 7

)

f ,&x'

)

+ M

)

&x'

)

x # 8

)

a ! 8n ! 2

# T

&x' ! 2 !

&x # 8' #

288

&x # 8'

! 2 !

&x # 8' #

288

&x # 8'

&x' ! f &8' !

f *&8'

&x # 8' !

f .&8'

&x # 8'

f ,&x' !

#8,3

f .&x' ! #

#5,3

f .&8' ! #

144

f *&x' !

#2,3

f *&8' !

f &x' !

! x

1,3

f &8' ! 2

7 + x + 9

a ! 8f &x' !

)

&x'

)

&n ! 1'!

)

x # a

)

n!1

)

&n!1'

&x'

)

+ M

)

&x'

)

786

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

Let’s use a graphing device to check the calculation in Example 1. Figure 2 shows that

the graphs of and are very close to each other when is near 8. Fig-

ure 3 shows the graph of computed from the expression

We see from the graph that

when . Thus the error estimate from graphical methods is slightly better than the

error estimate from Taylor’s Inequality in this case.

EXAMPLE 2

(a) What is the maximum error possible in using the approximation

when ? Use this approximation to ﬁnd correct to six decimal

places.

(b) For what values of is this approximation accurate to within ?

SOLUTION

(a) Notice that the Maclaurin series

is alternating for all nonzero values of , and the successive terms decrease in size

because , so we can use the Alternating Series Estimation Theorem. The error

in approximating by the ﬁrst three terms of its Maclaurin series is at most

If , then , so the error is smaller than

To ﬁnd we ﬁrst convert to radian measure.

Thus, correct to six decimal places, .

(b) The error will be smaller than if

)

5040

0.00005

sin 12- # 0.207912

# 0.20791169

sin 12- ! sin

180

! sin

sin 12-

&0.3'

5040

# 4.3 & 10

)

+ 0.3#0.3 + x + 0.3

)

5040

sin x

)

sin x ! x #

! " " "

0.00005x

sin 12-#0.3 + x + 0.3

sin x # x #

7 + x + 9

)

&x'

)

0.0003

)

&x'

)

# T

&x'

)

&x'

)

xy ! T

&x'y !

SECTION 12.11 APPLICATIONS OF TAYLOR POLYNOMIALS

|| ||

787

2.5

T™

„

F I G U R E 2

0.0003

7 9

y=|R™(x)|

F I G U R E 3

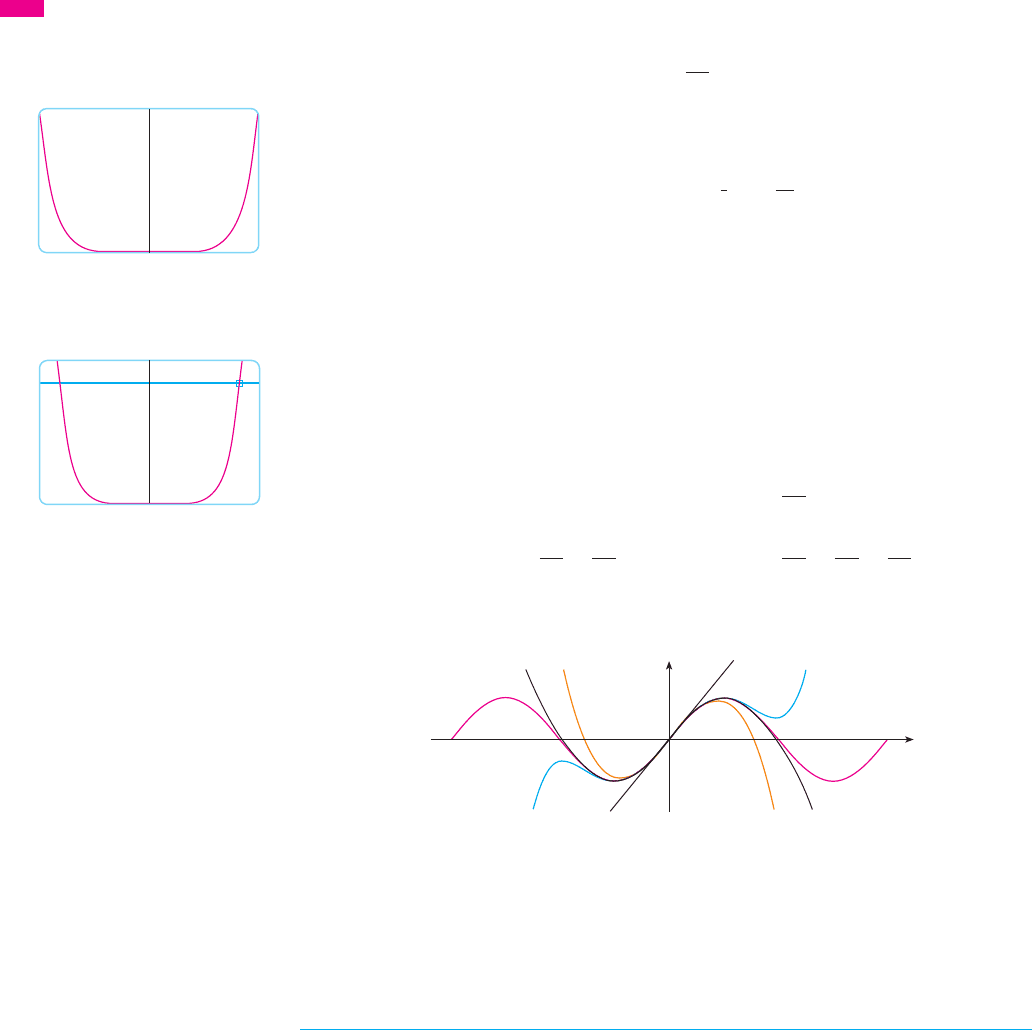
Solving this inequality for , we get

So the given approximation is accurate to within when . M

What if we use Taylor’s Inequality to solve Example 2? Since , we

have and so

So we get the same estimates as with the Alternating Series Estimation Theorem.

What about graphical methods? Figure 4 shows the graph of

and we see from it that when . This is the same estimate

that we obtained in Example 2. For part (b) we want , so we graph both

and in Figure 5. By placing the cursor on the right intersection

point we ﬁnd that the inequality is satisﬁed when . Again this is the same esti-

mate that we obtained in the solution to Example 2.

If we had been asked to approximate instead of in Example 2, it would

have been wise to use the Taylor polynomials at (instead of ) because they

are better approximations to for values of close to . Notice that is close to

(or radians) and the derivatives of are easy to compute at .

Figure 6 shows the graphs of the Maclaurin polynomial approximations

to the sine curve. You can see that as increases, is a good approximation to on

a larger and larger interval.

One use of the type of calculation done in Examples 1 and 2 occurs in calculators and

computers. For instance, when you press the or key on your calculator, or when a

computer programmer uses a subroutine for a trigonometric or exponential or Bessel func-

tion, in many machines a polynomial approximation is calculated. The polynomial is often

a Taylor polynomial that has been modiﬁed so that the error is spread more evenly through-

out an interval.

APPLICATIONS TO PHYSICS

Taylor polynomials are also used frequently in physics. In order to gain insight into an

equation, a physicist often simpliﬁes a function by considering only the ﬁrst two or three

terms in its Taylor series. In other words, the physicist uses a Taylor polynomial as an

sin

F I G U R E 6

T¶

T∞

T£

y=sin x

T¡

sin xT

&x'n

&x' ! x #

&x' ! x T

&x' ! x #

,3sin x

,360-

72-

,3xsin x

a ! 0a !

sin 12-sin 72-

)

0.82

y ! 0.00005y !

)

&x'

)

&x'

)

0.00005

)

+ 0.3

)

&x'

)

4.3 & 10

)

&x'

)

sin x #

(

x #

120

)

&x'

)

&7'

&x'

)

+ 1

&7'

&x' ! #cos x

)

0.820.00005

)

&0.252'

1,7

# 0.821or

)

0.252

788

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

Module 12.10 /12.11 graphically

shows the remainders in Taylor polynomial

approximations.

TE C

4.3 & 10–*

_0.3 0.3

y=|Rß(x)|

F I G U R E 4

0.00006

_1 1

y=|Rß(x)|

y=0.00005

F I G U R E 5

approximation to the function. Taylor’s Inequality can then be used to gauge the accuracy

of the approximation. The following example shows one way in which this idea is used in

special relativity.

EXAMPLE 3 In Einstein’s theory of special relativity the mass of an object moving

with velocity is

where is the mass of the object when at rest and is the speed of light. The kinetic

energy of the object is the difference between its total energy and its energy at rest:

(a) Show that when is very small compared with , this expression for agrees with

classical Newtonian physics: .

(b) Use Taylor’s Inequality to estimate the difference in these expressions for when

m,s.

SOLUTION

(a) Using the expressions given for and , we get

With , the Maclaurin series for is most easily computed as a

binomial series with .

(

Notice that because .

)

Therefore we have

and

If is much smaller than , then all terms after the ﬁrst are very small when compared

with the ﬁrst term. If we omit them, we get

(b) If , , and M is a number such that

, then we can use Taylor’s Inequality to write

We have and we are given that m,s, so

)

f .&x'

)

4&1 # v

5,2

4&1 # 100

5,2

&! M'

)

+ 100f .&x' !

&1 ! x'

#5,2

)

&x'

)

f .&x'

)

+ M

f &x' ! m

-&1 ! x'

#1,2

# 1.x ! #v

K # m

! m

! " " "

K ! m

1 !

! " " "

# 1

! 1 #

x !

! " " "

&1 ! x'

#1,2

! 1 #

x !

(

)(

)

(

)(

)

! " " "

)

1k ! #

&1 ! x'

#1,2

x ! #v

! m

1 #

#1,2

# 1

K ! mc

# m

1 # v

# m

)

+ 100

K !

Kcv

K ! mc

# m

m !

1 #

SECTION 12.11 APPLICATIONS OF TAYLOR POLYNOMIALS

|| ||

789

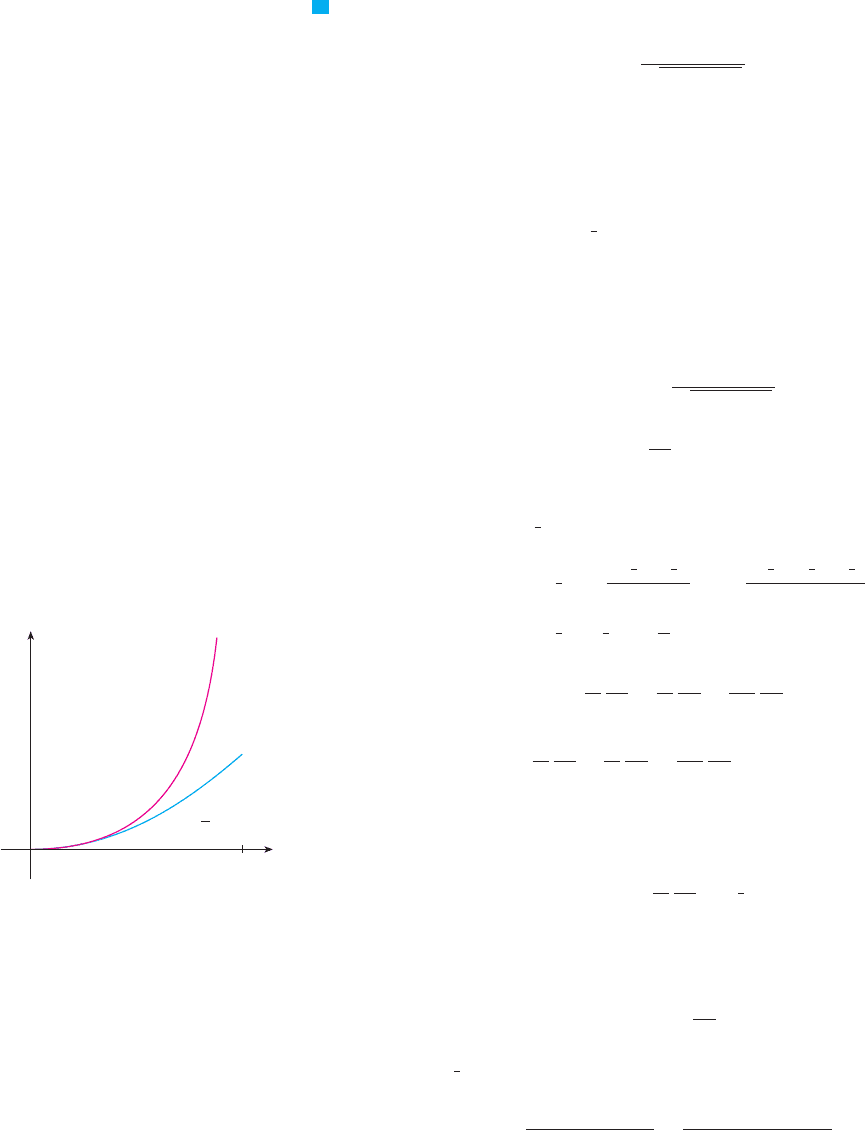
N The upper curve in Figure 7 is the graph of

the expression for the kinetic energy of an

object with velocity in special relativity. The

lower curve shows the function used for in

classical Newtonian physics. When is much

smaller than the speed of light, the curves are

practically identical.

F I G U R E 7

√

K=mc@-m¸c@

K= m¸√@

Thus, with ,

So when m!s, the magnitude of the error in using the Newtonian expression

for kinetic energy is at most .

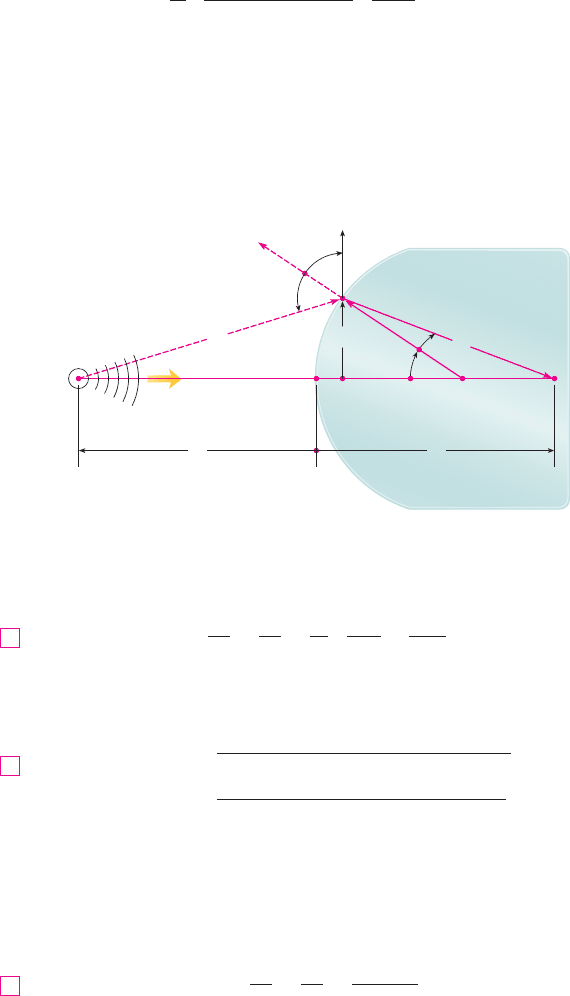
Another application to physics occurs in optics. Figure 8 is adapted from Optics,

4th ed., by Eugene Hecht (San Francisco: Addison-Wesley, 2002), page 153. It depicts a

wave from the point source S meeting a spherical interface of radius R centered at C. The

ray SA is refracted toward P.

Using Fermat’s principle that light travels so as to minimize the time taken, Hecht

derives the equation

where and are indexes of refraction and , , , and are the distances indicated in

Figure 8. By the Law of Cosines, applied to triangles ACS and ACP, we have

Because Equation 1 is cumbersome to work with, Gauss, in 1841, simpliﬁed it by using

the linear approximation for small values of . (This amounts to using the

Taylor polynomial of degree 1.) Then Equation 1 becomes the following simpler equation

[as you are asked to show in Exercise 34(a)]:

The resulting optical theory is known as Gaussian optics, or ﬁrst-order optics, and has

become the basic theoretical tool used to design lenses.

A more accurate theory is obtained by approximating by its Taylor polynomial of

degree 3 (which is the same as the Taylor polynomial of degree 2). This takes into account

rays for which is not so small, that is, rays that strike the surface at greater distances h

above the axis. In Exercise 34(b) you are asked to use this approximation to derive the

cos

# n

cos

" 1

" #s

# R$

" 2R#s

# R$ cos

" #s

" R$

# 2R#s

" R$ cos

C P

n¡ n™

Courtesy of Eugene Hecht

F I G U R E 8

Refraction at a spherical interface

#4.2 $ 10

#10

% 100

#x$

4#1 # 100

5!2

100

#4.17 $ 10

#10

c ! 3 $ 10

m!s

790

|| ||

CHAPTER 12 INFINITE SEQUENCES AND SERIES

N Here we use the identity

cos#

$ ! #cos

more accurate equation

The resulting optical theory is known as third-order optics.

Other applications of Taylor polynomials to physics and engineering are explored in

Exercises 32, 33, 35, 36, and 37 and in the Applied Project on page 793.

# n

" h

(

)

SECTION 12.11 APPLICATIONS OF TAYLOR POLYNOMIALS

|| ||

791

;

13. , , ,

14. , , ,

15. , , ,

16. , , ,

17. , , ,

, , ,

20. , , ,

21. , , ,

22. , , ,

23. Use the information from Exercise 5 to estimate cor-

rect to ﬁve decimal places.

24. Use the information from Exercise 16 to estimate

correct to ﬁve decimal places.

Use Taylor’s Inequality to determine the number of terms of

the Maclaurin series for that should be used to estimate

to within .

26. How many terms of the Maclaurin series for do you

need to use to estimate to within ?

;

27–29 Use the Alternating Series Estimation Theorem or

Taylor’s Inequality to estimate the range of values of for which

the given approximation is accurate to within the stated error.

Check your answer graphically.

27.

28.

29.

(

error

0.05

)

arctan x " x #

(

error

0.005

)

cos x " 1 #

(

error

0.01

)

sin x " x #

0.001ln 1.4

ln#1 " x$

0.00001

0.1

25.

sin 38(

cos 80(

#1 % x % 1n ! 5a ! 0f #x$ ! sinh 2x

#1 % x % 1n ! 4a ! 0f #x$ ! x sin x

0.5 % x % 1.5n ! 3a ! 1f #x$ ! x ln x

0 % x % 0.1n ! 3a ! 0f #x$ ! e

19.

0.5 % x % 1.5n ! 3a ! 1f #x$ ! ln#1 " 2x$

18.

#0.2 % x % 0.2n ! 2a ! 0f #x$ ! sec x

0 % x %

!3n ! 4a !

!6f #x$ ! sin x

0.8 % x % 1.2n ! 3a ! 1f #x$ ! x

2!3

0.9 % x % 1.1n ! 2a ! 1f #x$ ! x

4 % x % 4.2n ! 2a ! 4f #x$ !

#x$

;

1. (a) Find the Taylor polynomials up to degree 6 for

centered at . Graph and these

polynomials on a common screen.

(b) Evaluate and these polynomials at , ,

and .

to .

;

2. (a) Find the Taylor polynomials up to degree 3 for

centered at . Graph and these

polynomials on a common screen.

(b) Evaluate and these polynomials at and 1.3.

to .

;

3–10 Find the Taylor polynomial for the function at the

number . Graph and on the same screen.

3. ,

4. ,

6. ,

7. ,

8. ,

10. ,

11–12 Use a computer algebra system to ﬁnd the Taylor poly-

nomials centered at for . Then graph these

polynomials and on the same screen.

11. ,

12. ,

13–22

(a) Approximate by a Taylor polynomial with degree at the

number .

(b) Use Taylor’s Inequality to estimate the accuracy of the

approximation when x lies in the given

interval.

f #x$ " T

#x$

a ! 0f #x$ !

1 " x

a !

!4f #x$ ! cot x

n ! 2, 3, 4, 5aT

CAS

a ! 1f #x$ ! tan

a ! 0f #x$ ! xe

#2x

a ! 1f #x$ !

ln x

a ! 0f #x$ ! arcsin x

a ! 0f #x$ ! e

sin x

a !

!2f #x$ ! cos x

a ! 0f #x$ ! x " e

a ! 2f #x$ ! 1!x

#x$

f #x$

x ! 0.9f

fa ! 1f #x$ ! 1!x

f #x$

!2x !

!4f

fa ! 0f #x$ ! cos x

E X E R C I S E S

12.11