Stewart J. College Algebra: Concepts and Contexts
Подождите немного. Документ загружается.

334 CHAPTER 4
■
Logarithmic Functions and Exponential Models
47–50
■ The graph of a logarithm function is shown. Find the base a.
47. 48.
f 1x 2= log
a
x
x
y
0
1 5
(5, 1
)
1
x
y
0
12345678910
(8, 1)
1.0
51. Graph the family of logarithmic functions for . How are the
graphs related?
52. Graph the functions and . How are the graphs related?g1x 2= log
10
110x 2f 1x 2= log
10
x
a = 3, 5, 7f 1x 2= log
a
x
0
x
y
1 963
(9, 2)
1
x
y
0
1
3
1
!
3,
@
1
2
2
4.2 Laws of Logarithms
■
Laws of Logarithms
■
Expanding and Combining Logarithmic Expressions
■
Change of Base Formula
IN THIS SECTION… we study the Laws of Logarithms. These laws are the properties of
logarithms that correspond to the Rules of Exponents.
The Laws of Logarithms are the key properties of logarithms. They allow us to use
logarithms to compare large numbers (Section 4.3) and to solve exponential equa-
tions (Section 4.5). We need to solve exponential equations to answer questions such
as “When will my bank account reach a million dollars?” or “When will the popula-
tion of the world reach 10 billion?”
2
■ Laws of Logarithms
Since logarithms are exponents, the Rules of Exponents give us useful rules for
working with logarithms. For example, we know that
“To find the product of two powers with the same base, we add exponents.”
For example, . To see what this rule tells us about logarithms, let’s
express the exponents as logarithms. So let
A = 10
x
B = 10
y
AB = 10
x +y
10
x
#
10
y
= 10
x +y
The Rules of Exponents are
reviewed in Algebra Toolkit A.3,
page T14.
49. 50.

SECTION 4.2
■
Laws of Logarithms 335
Law In Words
1. The logarithm of a product is the sum of
the logarithms.
2. The logarithm of a quotient is the
difference of the logarithms.
3. The logarithm of a power is the exponent
times the logarithm of the base.
log
a
A
C
= C log
a
A
log
a
˛
A
B
= log
a
A - log
a
B
log
a
AB = log
a
A + log
a
B
Writing these equations in logarithmic form, we get
It follows that . We can express this rule in words:
“To find the logarithm of a product, we add the logarithms of the factors.”
This explains the first of the following “laws.” Laws 2 and 3 follow from the corre-
sponding rules for exponents. In these laws A and B are positive real numbers, and
C is any real number.
Laws of Logarithms
log
10
AB = log
10
A + log
10
B
log
10
A = xlog
10
B = ylog
10
AB = x + y
example
1
Evaluating Logarithmic Expressions
Evaluate each expression.
(a)
(b)
(c)
Solution
To find the logarithm of a number, it’s helpful to express the number as a power of
the base.
(a) Law 1
Because
(b) Law 2
Because
(c) Law 3
Rules of Exponents
Calculator
■ NOW TRY EXERCISE 9 ■
L-0.301
= logA
1
2
B
-
1
3
log 8 = log 8
-1>3
16 = 2
4
= log
2
16 = 4
log
2
80 - log
2
5 = log
2
A
80
5
B
64 = 4
3
= log
4
64 = 3
log
4
2 + log
4
32 = log
4
12
#
322
-
1
3
log 8
log
2
80 - log
2
5
log
4
2 + log
4
32
8
-1>3
=
1
8
1>3
=
1
2
2
■ Expanding and Combining Logarithmic Expressions
The Laws of Logarithms allow us to write the logarithm of a product or a quotient
as a sum or difference of logarithms. This process, called expanding a logarithmic
expression, is illustrated in the next example.

336 CHAPTER 4
■
Logarithmic Functions and Exponential Models
example
2
Expanding Logarithmic Expressions
Use the Laws of Logarithms to expand each expression.
(a) (b) (c) (d)
Solution
(a) Law 1
(b) Law 2
Law 3
(c) Law 1
Law 3
(d) Law 2
Law 1
Law 3
■ NOW TRY EXERCISES 11 AND 15 ■
The Laws of Logarithms also allow us to reverse the process of expanding. That
is, we can write sums and differences of logarithms as a single logarithm. This process,
called combining logarithmic expressions, is illustrated in the next example.
= log a + log b -
1
3
log c
= log a + log b - log c
1>3
log
ab
2
3
c
= log ab - log2
3
c
= 3 log
5
x + 6 log
5
y
log
5
x
3
y
6
= log
5
x
3
+ log
5
y
6
= 2 log
4
z - log
4
y
log
4
z
2
y
= log
4
z
2
- log
4
y
log
2
6x = log
2
6 + log
2
x
log
ab
2
3
c
log
5
x
3
y
6
log
4
z
2
y
log
2
6x
example
3
Combining Logarithmic Expressions
Combine the given expression into a single logarithm.
(a) (b)
Solution
(a) Law 3
Law 1
(b) Law 3
Law 2
■ NOW TRY EXERCISE 19 ■
= log a
s
3
2t + 1
b
3 log s -
1
2
log1t + 1 2= log s
3
- log1t + 12
1>2
= log1x
3
1x - 5 2
2
2
3 log x + 2 log1x - 52= log x
3
+ log1x - 5 2
2
3 log s -
1
2
log1t + 123 log x + 2 log1x - 5 2
example
4
Comparing Logarithms
Find the difference in the logarithms of the given weights (subtract the smaller log-
arithm from the larger one).
(a) The weight of a beetle is 10 times that of an ant.
(b) The weight of a mouse is a thousandth that of a wolf.
Recall that log x is the common
logarithm and is the same as .log
10
x
SECTION 4.2
■
Laws of Logarithms 337
Solution
(a) Let A be the weight of the ant. Then the weight of the beetle is 10A. The
difference in the logarithms is
Law 2
Simplify
Because
The difference in the logarithms is 1.
(b) Let W be the weight of the wolf. Then the weight of the mouse is .
The difference in the logarithms is
Law 2
Simplify
Because
The difference in the logarithms is 3.
■ NOW TRY EXERCISES 25 AND 29 ■
1000 = 10
3
= 3
= log1000
log1W 2- log a
W
1000
b= logW - 1logW - log1000 2
W>1000
10 = 10
1
= 1
= log10
log110A 2- log A = log a
10A
A
b
2
■ Change of Base Formula
So far, we have been calculating logarithms by inspection or by using the calculator.
That’s fine when the numbers involved are exact powers of the base—for example,
because we know that . But what if we need to find, say, ?
Scientific calculators in general have only two keys that calculate logarithms:
for finding logarithms base 10 and for finding logarithms base e. (We’ll learn
about in Section 4.4.) We can use a calculator to find logarithms for other bases
by using the Change of Base Formula.
Change of Base Formula
LN
LN
lOG
log
3
172
4
= 16log
2
16 = 4
log
b
x =
log
a
x
log
a
b
To prove this formula, we’ll start with the logarithm that we want to find. Let
We write this equation in exponential form and take the logarithm, with base a, of
each side.
Exponential form
Take of each side
Law 3
Divide by
Since , this completes the proof.y = log
b
x
log
a
b y =
log
a
x
log
a
b
y log
a
b = log
a
x
log
a
log
a
1b
y
2= log
a
x
b
y
= x
y = log
b
x

338 CHAPTER 4
■
Logarithmic Functions and Exponential Models
example
5
Evaluating Logarithms with the Change of Base Formula
Use the Change of Base Formula to evaluate the logarithm , correct to five dec-
imal places.
Solution
We use the Change of Base Formula with , , and .
Change of Base Formula
Calculator
■ NOW TRY EXERCISE 33 ■
Graphing calculators have a key for calculating logarithms base 10. We
can use a graphing calculator to draw a graph for any base a by us-
ing the Change of Base Formula. For example, to draw a graph of ,
we note that
This shows that is a constant multiple of , that is, .
We use this fact to sketch graphs of logarithm functions in the next example.
log
4
x L 11.662 log xlog xlog
4
x
f 1x2= log
4
x =
log x
log 4
= a
1
log 4
b log x L 11.662 log x
f 1x2= log
4
x
f 1x2= log
a
x
lOG
L 0.77398
log
8
5 =
log
10
5
log
10
8
x = 5a = 10b = 8
log
8
5
example
6
Graphing Logarithmic Functions
Using the Change of Base Formula
Draw the graph of the family of logarithmic functions for
, all on the same graph.
Solution
To draw a graph of using a graphing calculator, we first use the Change
of Base Formula:
Change of Base Formula
Rewrite the fraction
Calculator
Similarly, you can check that
f 1x2= log
5
x L 11.432 log x
f 1x2= log
3
x L 12.102 log x
L 13.322 log x
= a
1
log 2
b log x
log
2
x =
log x
log 2
y = log
2
x
a = 2, 3, 5, 10
f 1x2= log
a
x
We can now evaluate a logarithm to any base by using the Change of Base
Formula to express the logarithm in terms of common logarithms and then using a
calculator.

SECTION 4.2
■
Laws of Logarithms 339
3
_3
_1
5
y=log¤x
y=log‹x
y=log⁄‚x
y=logfix
figure 1 A family of logarithmic
functions
Using a graphing calculator, we sketch these graphs in Figure 1. Notice how in-
creasing the value of the base a affects the graph.
■ NOW TRY EXERCISES 37 AND 39 ■
4.2 Exercises
CONCEPTS
Fundamentals
1. The logarithm of a product of two numbers is the same as the _______ of the
logarithms of these numbers. So
_______⫹ _______.
2. The logarithm of a quotient of two numbers is the same as the
_______ of the
logarithms of these numbers. So
_______ ⫺ _______.
3. The logarithm of a number raised to a power is the same as the logarithm of the number
multiplied by the
_______. So _______.
4. Most calculators can find logarithms with base
_______. To find logarithms with
different bases, we use the
_____________ Formula. To find , we write
_____________.
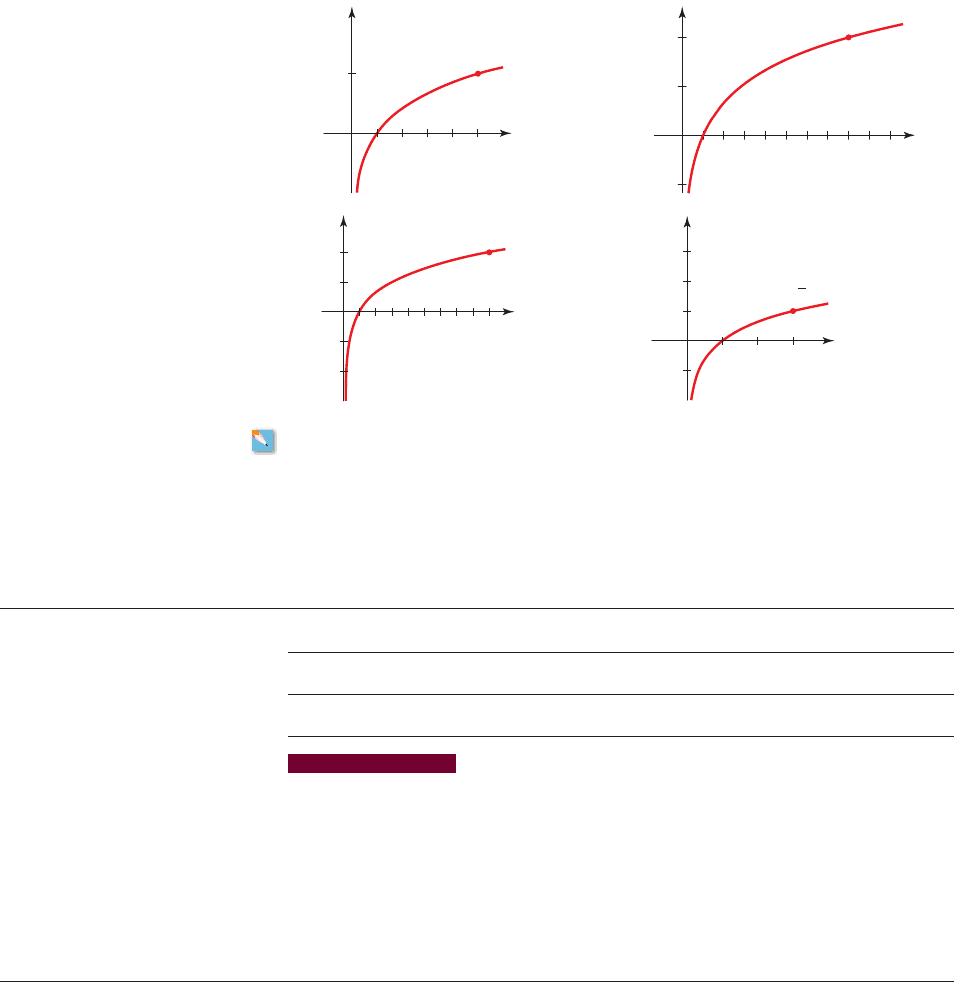
5. Match the logarithmic function with its graph.
(a) (b) (c) f 1x 2= log
5
xf 1x 2= log
2
xf 1x 2= log
10
x
log
7
12 =
log
ⵧ
log
ⵧ
=
log
7
12
log
5
125
10
2=
log
5
A
25
125
B=
log
5
125
#
1252=
x
y
1
2
4
3
12468357911
I
II
III
10
0
_1

340 CHAPTER 4
■
Logarithmic Functions and Exponential Models
SKILLS
6. When using a graphing calculator to draw the graph of the function , first
rewrite f as a constant multiple of the common logarithm function, using the
______________ Formula:
Think About It
7. True or false? (Assume that x, y, a, b are positive numbers.)
(a) (b)
(c) (d)
(e) (f)
(g) (h)
8. How are the graphs of and related? Answer this
question without using a graphing calculator. [Hint: Use the Laws of Logarithms.]
9–10
■ Evaluate the given expression.
9. (a) (b) (c)
10. (a) (b) (c)
11–18 ■ Use the Laws of Logarithms to expand the given expression.
11. (a) (b)
12. (a) (b)
13. (a) (b)
14. (a) (b)
15. (a) (b)
16. (a) (b)
17. (a) (b)
18. (a) (b)
19–24
■ Use the Laws of Logarithms to combine the given expression.
19. (a)
(b)
20. (a)
(b) log 5 + 2 log x + 3 log1x
2
+ 52
4 log
2
x -
1
3
log
2
1x
2
+ 12
4 log
6
y -
1
4
log
6
z
log
2
A + log
2
B - 2 log
2
C
log a
x
3
y
4
z
6
blog 2
3
3r
2
s
log
5
a
x
2
yz
3
blog1xy2
10
log
7
2
3
wz
x
log1w
2
z2
10
log
r
3
s
4
2
4
t
log
2
s
2
1t
log
5
2a
b
log
3
15a 2
log a
1
1z
blog
2
1AB
2
2
log
3
1x 1y2log
5
x
2
log
3
x
y
3
log
2
2x
1
2
log
5
625 - 3 log
5
15log
4
192 - log
4
3log
12
9 + log
12
16
-
1
2
log
2
64log
2
160 - log
2
5log
10
4 + log
10
25
g1x 2= 1 + log xf 1x 2= log110x2
2 log x = log x
2
1log x 2
2
= log x
2
log
2
1x - y 2= log
2
x - log
2
y
log a
log b
= log a - log b
log1x + y2= log x + log ylog x + log y = log xy
log a - log b = log a
a
b
blog a
x
y
b=
log x
log y
f 1x2= a
1
log
ⵧ
b log x
f 1x 2= log
13
x
SECTION 4.2
■
Laws of Logarithms 341
21. (a)
(b)
22. (a)
(b)
23. (a)
(b)
24. (a)
(b)
25–28
■ Find the difference in the logarithms of the given weights. (Subtract the smaller
logarithm from the larger one.)
25. The weight of an elephant is 100,000 times as much as the weight of a mouse.
26. The weight of an average star is times as much as the weight of a hippopotamus.
27. The weight of a bacterium is about times as much as the weight of an atom.
28. The weight of an electron is one thousandth the weight of an atom.
29–32
■ Find the difference in the logarithms of the given heights or lengths. (Subtract the
smaller logarithm from the larger one.)
29. The length of a ladybug is one thousandth of the height of a giraffe.
30. The height of a human is times the diameter of a bacterium.
31. The height of a tree is 100 times the height of a rabbit.
32. The radius of the earth is one hundredth of the radius of the sun.
33–36
■ Use the Change of Base Formula and a calculator to evaluate the logarithm,
correct to six decimal places.
33. (a) (b)
34. (a) (b)
35. (a) (b)
36. (a) (b)
37–38
■ Use the Change of Base Formula to draw a graph of the function (see Example 6).
37. (a) (b)
38. (a) (b)
39–40 ■ Draw graphs of the family of logarithmic functions , for the given
values of a, all in the same viewing rectangle (see Example 6). How are these
graphs related?
39. 40.
41–42
■ A family of functions is given.
(a) Graph the family for .
(b) How are the graphs in part (a) related?
41. 42. H1x2= c log xG1x 2= log1cx 2
c = 1, 2, 3, 4
a = 3, 5, 7a = 2, 4, 6
f 1x 2= log
a
x
g1x 2= log
8
xg1x2= log
6
x
f 1x 2= log
9
xf 1x2= log
5
x
log
12
2.5log
4
125
log
6
532log
7
2.61
log
6
92log
3
16
log
5
2log
2
5
10
6
10
15
10
27
log1a + b2+ log1a - b 2- 2 log c
log
7
1s + 12-
1
3
log
7
1s - 12
4 log x -
1
3
log1x
2
+ 12+ 2 log1x - 12
1
2
log
4
1y + 12-
1
2
log
4
1y - 12
log
5
1x
2
- 12- log
5
1x - 12
2 log
8
1x + 12+ 2 log
8
1x - 12
4 log
3
12x - 12-
1
2
log
3
1x + 12
2
3 log
2
A + 2 log
2
1B + 12

342 CHAPTER 4
■
Logarithmic Functions and Exponential Models
2
■ Logarithmic Scales
We have observed that when numbers vary over a large range, their logarithms vary
over a much smaller range. For example, the logarithms of the numbers between
and vary between and 6. So to manage and understand large ranges of num-
bers, we represent them on a “logarithmic ruler” or logarithmic scale. An ordinary
ruler uses a linear scale: Each successive mark on the ruler adds a fixed constant. On
a “logarithmic ruler” each successive mark multiplies by a fixed factor. (See Figure 1.)
Linear scale: Each successive mark on the scale corresponds to adding a
fixed constant.
Logarithmic scale: Each successive mark on the scale corresponds to
multiplying by a fixed factor.
For example, for a logarithmic scale in base 10, moving up one unit on the scale cor-
responds to multiplying by 10. So the marks on the logarithmic ruler are the loga-
rithms of the numbers they represent. The marks at 2, 3, and 4 on the ruler represent
100, 1000, and 10000, respectively. (Logarithmic scales can be made in any base, but
the most common base is 10.)
- 310
6
10
-3
figure 1 The marks on the “logarithmic ruler” are the logarithms of the
number they represent.
0
10º
1
10¡
2
10™
3
10£
4
10¢
5
10∞
6
10§
2
4.3 Logarithmic Scales
■
Logarithmic Scales
■
The pH Scale
■
The Decibel Scale
■
The Richter Scale
IN THIS SECTION… we see how logarithms allow us to efficiently compare real-world
phenomena that vary over extremely large ranges (logarithmic scales).
Many real-world quantities involve a huge disparity in size. For example, an average-
sized human is many times larger than an atom but trillions of times smaller than the
smallest star, which in turn is insignificantly small in comparison to the average
galaxy. So how can we meaningfully compare these very different sizes? How can
we represent these differing sizes graphically?
Even everyday activities can involve enormously varying sizes. For example,
our ears are sensitive to huge variations in sound intensity; we can hear a soft whis-
per as well as the almost deafening roar of a jet engine. The sound of a jet engine is
a million billion times more intense than a whisper. We’ll see in this section that the
key to comparing and visualizing these vast disparities in size is to use logarithms.
AP Images
SECTION 4.3
■
Logarithmic Scales 343
example
1
Logarithmic Scale
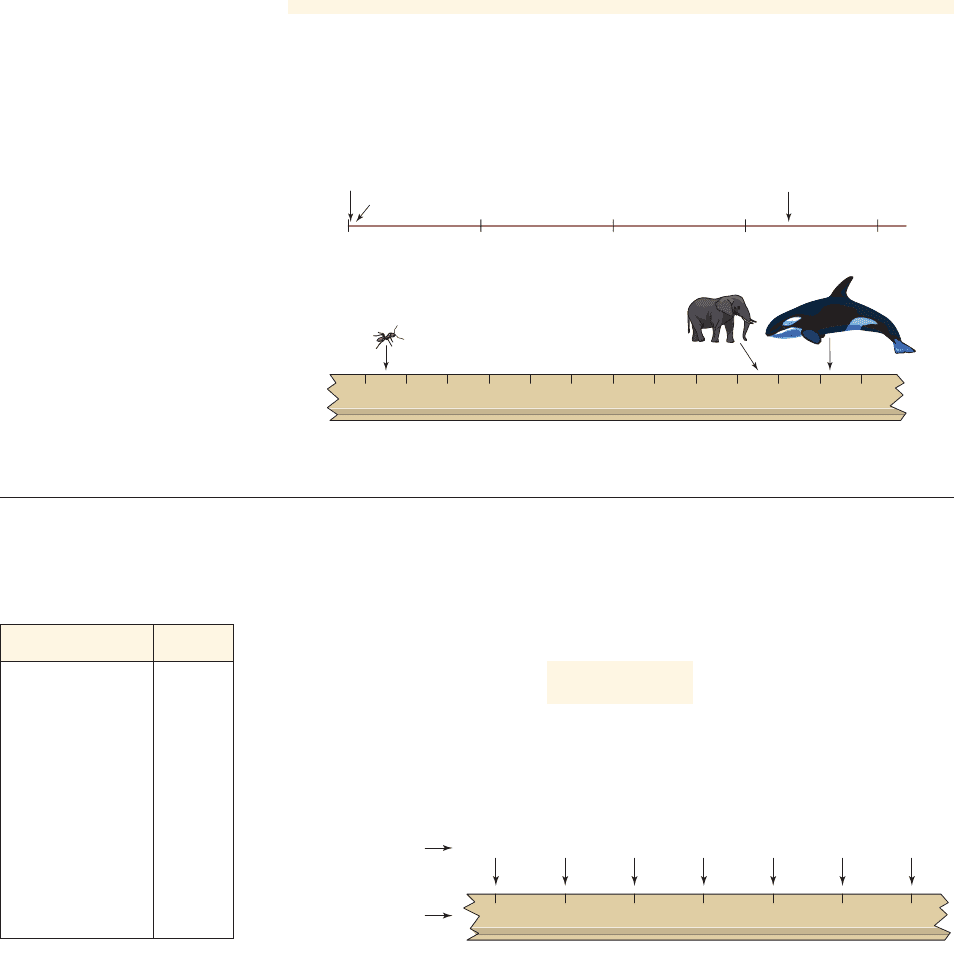
The weights of a particular ant, elephant, and whale are given. Compare the weights
on a logarithmic scale (see Example 3 in Section 4.1, page 326).
Ant 0.000003 kilograms
Elephant 4000 kilograms
Whale 170,000 kilograms
Solution
On a logarithmic scale, these weights are represented by their logarithms. So on a
logarithmic scale, the weights are represented by , and 5.2, respectively.
■ NOW TRY EXERCISE 7 ■
In Figure 2 we represent the weights of the ant, elephant, and whale of Example 1
graphically. On a linear scale, the weight of the ant is indistinguishable from 0 and from
the weight of the elephant. On a logarithmic scale we can more easily gauge their rela-
tive sizes.
- 5.5, 3.6
0
0 50,000 100,000 150,000
WhaleAnt
Elephant
200,000
1 2 3 4 5 6_6 _5 _4 _3 _2 _1
figure 2 A linear scale (top) and a logarithmic scale (bottom).
2
■ The pH Scale
Chemists measure the acidity of a solution by giving its hydrogen ion concentration
in moles per liter (M). The hydrogen ion concentration varies greatly from sub-
stance to substance and involves huge numbers. In 1909 Sorensen proposed using a
logarithmic scale to measure hydrogen ion concentration. He defined
He did this to avoid very small numbers and negative exponents. For instance,
In other words, the pH scale is a “logarithmic ruler” for measuring ion concentration.
If
3H
+
4= 10
-4
MthenpH =-log
10
110
-4
2=-1- 42= 4
pH =-log 3H
+
4
3H
+
4
4
10–¢
pH
Ion concentration
5
10–∞
6
10–§
7
10–¶
8
10–•
9
10–ª
10
10–¡º
Substance pH
Milk of magnesia 10.5
Seawater 8.0–8.4
Human blood 7.3–7.5
Crackers 7.0–8.5
Hominy (lye) 6.9–7.9
Cow’s milk 6.4–6.8
Spinach 5.1–5.7
Tomatoes 4.1–4.4
Oranges 3.0–4.0
Apples 2.9–3.3
Limes 1.3–2.0
Battery acid 1.0
pH for some common substances
