Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

15.2 Geometry of SU(2) 545

Exercise 15.8: Show that for U, the defining 2-by-2 matrices of SU(2), we have



SU(2)

−1

dU )

= 24π

Suppose we have a map g : R

→ SU(2) such that g(x) goes to the identity element at

infinity. Consider the integral

S[g]=

24π



tr (g

−1

dg)

where the 3-form tr (g

−1

dg)

is the pull-back to R

of the form tr [(U

−1

dU )

]on SU(2).

Show that if we make the variation g → g + δg, then

δS[g]=

24π





3tr



−1

δg)(g

−1

dg)



= 0,

and so S[g] is a topological invariant of the map g. Conclude that the functional S[g]

is an integer, that integer being the Brouwer degree, or winding number, of the map

g : S

→ S

Exercise 15.9: Generalize the result of the previous problem to show, for any mapping

x (→ g(x) into a Lie group G, and for n an odd integer, that the n-form tr (g

−1

dg)

constructed from the Maurer–Cartan form is closed, and that

δ tr (g

−1

dg)

= d



n tr



−1

δg)(g

−1

dg)

n−1



(Note that for even n the trace of (g

−1

dg)

vanishes identically.)

15.2.5 SO(3) * SU(2)/Z

The groups SU(2) and SO(3) are locally isomorphic. They have the same Lie algebra,

but differ in their global topology. Although rotations in space are elements of SO(3),

electrons respond to these rotations by transforming under the two-dimensional defining

representation of SU(2). As we shall see, this means that after a rotation through 2π the

electron wavefunction comes back to minus itself. The resulting orientation entanglement

is characteristic of the spinor representation of rotations and is intimately connected

with the Fermi statistics of the electron. The spin representations were discovered by

Élie Cartan in 1913, some years before they were needed in physics.

The simplest way to motivate the spin/rotation connection is via the Pauli sigma

matrices. These matrices are hermitian, traceless and obey

=σ

+=σ

=σ

= 2δ

I. (15.63)

546 15 Lie groups

If, for any U ∈ SU(2), we define

=σ



= U=σ

−1

, (15.64)

then the =σ



are also hermitian, traceless and obey (15.63). Since the original =σ

form a

basis for the space of hermitian traceless matrices, we must have

=σ



= =σ

(15.65)

for some real 3-by-3 matrix having entries R

. From (15.63) we find that

2δ

= =σ



=σ



+=σ



=σ



= (=σ

)(=σ

) + (=σ

)(=σ

)

= (=σ

=σ

+=σ

=σ

= 2δ

Thus

= δ

. (15.66)

In other words, R

R = I, and so R is an element of O(3). Now the determinant of any

orthogonal matrix is ±1, but the manifold of SU(2) is a connected set and R = I when

U = I. Since a continuous map from a connected set to the integers must be a constant,

we conclude that det R = 1 for all U . The R matrices are therefore in SO(3).

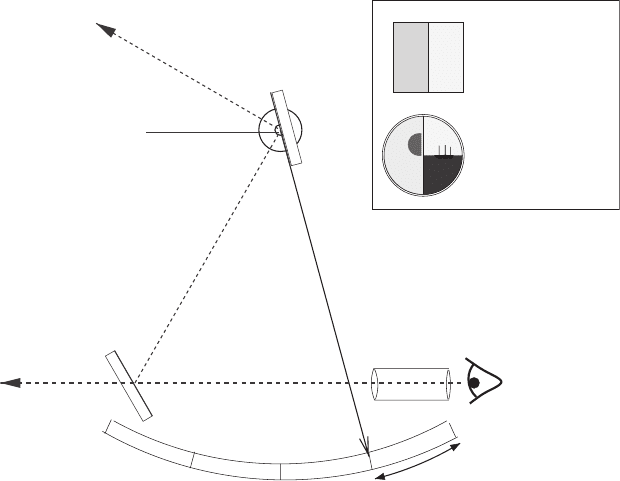
We now exploit the principle of the sextant to show that the correspondance goes both

ways, i.e. we can find a U (R) for any element R ∈ SO(3). This familiar instrument is

used to measure the altitude of the Sun above the horizon while standing on the unsteady

deck of a ship at sea (Figure 15.1). A theodolite or similar device would be rendered

useless by the ship’s pitching and rolling. The sextant exploits the fact that successive

reflection in two mirrors inclined at an angle θ to one another serves to rotate the image

through an angle 2θ about the line of intersection of the mirror planes. This rotation

is used to superimpose the image of the sun onto the image of the horizon, where it

stays even if the instrument is rocked back and forth. Exactly the same trick is used in

constructing the spinor representations of the rotation group.

Consider a vector x with components x

and form the matrix

x = x

=σ

. Now, if n is a

unit vector with components n

, then

(−=σ

)

x(=σ

) =



− 2(n · x)(n

)



=σ

x − 2(n · x )

n. (15.67)

The vector x − 2(n · x)n is the result of reflecting x in the plane perpendicular to n.

Consequently

−(=σ

cos θ/2 +=σ

sin θ/2)(−=σ

)

x (=σ

)(=σ

cos θ/2 +=σ

sin θ/2) (15.68)

15.2 Geometry of SU(2) 547

Left-hand half of fixed

mirror is silvered. Right-

hand half is transparent

View through telescope

of Sun brought down to

touch horizon

120º

90º

60º

30º

0º

Pivot

Moveable Mirror

2

Telescope

To Sun

To Horizon

Fixed, half-silvered mirror

Figure 15.1 The sextant. The telescope and the half-silvered mirror are fixed to the frame of the

instrument, which also holds the scale. The second mirror and attached pointer pivot so that the

angle θ between the mirrors can be varied and accurately recorded. The scale is calibrated so as

to display the altitude 2θ. For the configuration shown, θ = 15

◦

while the pointer indicates that

the sun is 30

◦

above the horizon.

performs two successive reflections on x. The first, a reflection in the “1” plane, is

performed by the inner =σ

’s. The second reflection, in a plane at an angle θ/2 to the “1”

plane, is performed by the (=σ

cos θ/2 +=σ

sin θ/2)’s. Multiplying out the factors, and

using the =σ

algebra, we find

(cos θ/2 −=σ

=σ

sin θ/2)

x(cos θ/2 +=σ

=σ

sin θ/2)

= =σ

(cos θ x

− sin θ x

) +=σ

(sin θ x

+ cos θ x

) +=σ

. (15.69)

The effect on x is a rotation

(→ cos θ x

− sin θ x

(→ sin θ x

+ cos θ x

(→ x

, (15.70)

through the angle θ about the 3-axis. We can drop the x

and re-express (15.69)as

U=σ

−1

= =σ

, (15.71)

548 15 Lie groups

where R

is the 3-by-3 rotation matrix

R =

⎛

⎝

cos θ −sin θ 0

sin θ cos θ 0

001

⎞

⎠

, (15.72)

and

U = exp



−

=σ



= exp



−i

[=σ

,=σ

]θ



(15.73)

is an element of SU(2). We have exhibited two ways of writing the exponents in (15.73)

because the subscript 3 on=σ

indicates the axis about which we are rotating, while the 1, 2

in [=σ

,=σ

] indicates the plane in which the rotation occurs. It is the second language that

generalizes to higher dimensions. More on the use of mirrors for creating and combining

rotations can be found in §41.1 of Misner, Thorne and Wheeler’s Gravitation.

This mirror construction shows that for any R ∈ SO(3) there is a two-dimensional

unitary matrix U(R) such that

U (R)=σ

−1

(R) = =σ

. (15.74)

This U (R) is not unique, however. If U ∈ SU(2) then so is −U. Furthermore

U (R)=σ

−1

(R) = (−U (R))=σ

(−U (R))

−1

, (15.75)

and so U(R) and −U (R) implement exactly the same rotation R. Conversely, if two

SU(2) matrices U , V obey

U σ

−1

= V σ

−1

(15.76)

then V

−1

U commutes with all 2-by-2 matrices and, by Schur’s lemma, must be a

multiple of the identity. But if λI ∈ SU(2) then λ =±1. Thus, U =±V . The mapping

between SU(2) and SO(3) is therefore two-to-one. Since U and −U correspond to the

same R, the group manifold of SO(3) is the 3-sphere with antipodal points identified.

Unlike the 2-sphere, where the identification of antipodal points gives the non-orientable

projective plane, the SO(3) group manifold remains orientable. It is not, however, simply

connected: a path on the 3-sphere from a point to its antipode forms a closed loop in

SO(3), but one that is not contractible to a point. If we continue on from the antipode

back to the original point, the complete path is contractible. This means that the first

homotopy group, the group π

(SO(3)) of based paths in SO(3) with composition given

by concatenation, is isomorphic to Z

. This two-element group encodes the topology

behind the Balinese Candle Dance, and keeps track of whether a sequence of rotations

that eventually bring a spin-

particle back to its original orientation should be counted

as a 360

◦

rotation (U =−I )ora720

◦

∼ 0

◦

rotation (U =+I ).

15.2 Geometry of SU(2) 549

Exercise 15.10: Verify that

U (R)=σ

−1

(R) = =σ

is consistent with U (R

)U (R

) =±U (R

Spinor representations of SO(N )

The mirror trick can be extended to perform rotations in N dimensions. We replace the

three =σ

matrices by a set of N Dirac gamma matrices, which obey the defining relations

of a Clifford algebra:

=γ

+ =γ

=γ

= 2δ

µν

I. (15.77)

These relations are a generalization of the key algebraic property of the Pauli sigma

matrices.

If N (= 2n) is even, then we can find 2

-by-2

hermitian matrices =γ

satisfying this

algebra. If N (= 2n + 1) is odd, we append to the matrices for N = 2n the hermitian

matrix =γ

2n+1

=−(i)

=γ

···=γ

which obeys =γ

2n+1

= 1 and anticommutes with all

the other =γ

. The =γ matrices therefore act on a 2

0N /21

-dimensional space, where the

symbol 0N /21 denotes the integer part of N /2.

The =γ ’s do not form a Lie algebra as they stand, but a rotation through θ in the µν-plane

is obtained from

exp



−i

[=γ

, =γ

]θ



=γ

exp



[=γ

, =γ

]θ



= =γ

, (15.78)

and we find that the hermitian matrices



µν

[=γ

, =γ

] form a basis for the Lie

algebra of SO(N ). The 2

0N /21

-dimensional space on which they act is the Dirac spinor

representation of SO(N ). Although the matrices exp{i



µν

} are unitary, they are not

the entirety of U(2

0N /21

), but instead constitute a subgroup called Spin(N ).

If N is even then we can still construct the matrix =γ

2n+1

that anti-commutes with all

the other =γ

’s. It cannot be the identity matrix, therefore, but it commutes with all the



µν

. By Schur’s lemma, this means that the SO(2n) Dirac spinor representation space

V is reducible. Now, =γ

2n+1

= I, and so =γ

2n+1

has eigenvalues ±1. The two eigenspaces

are invariant under the action of the group, and thus the Dirac spinor space decomposes

into two irreducible Weyl spinor representations:

V = V

odd

⊕ V

even

. (15.79)

Here V

even

and V

odd

, the plus and minus eigenspaces of =γ

2n+1

, are called the spaces of

right and left chirality. When N is odd the spinor representation is irreducible.

550 15 Lie groups

Exercise 15.11: Starting from the defining relations of the Clifford algebra (15.77) show

that, for N = 2n,

tr (=γ

) = 0,

tr (=γ

2n+1

) = 0,

tr (=γ

=γ

) = tr (I )δ

µν

tr (=γ

=γ

) = 0,

tr (=γ

=γ

) = tr (I )(δ

µν

στ

− δ

µσ

ντ

+ δ

µτ

νσ

Exercise 15.12: Consider the space (C) =



symmetric tensors A

...µ

for 0 ≤ p ≤ N = 2n. Let

αβ



p=0



=γ

···=γ



αβ

...µ

define a mapping from (C) into the space of complex matrices of the same size as the

=γ

. Show that this mapping is invertible, i.e. given ψ

αβ

we can recover the A

...µ

.By

showing that the dimension of (C) is 2

, deduce that the =γ

must be at least 2

-by-2

matrices.

Exercise 15.13: Show that the R

Dirac operator D = =γ

∂

obeys D

=∇

. Recall

that the Hodge operator d −δ from Section 13.7.1 is also a “square root” of the Laplacian:

(d − δ)

=−(dδ + δd) =∇

Show that

αβ

→ (Dψ)

αβ

= (=γ

)

αα



∂



corresponds to the action of d − δ on the space (R

, C) of differential forms

A =

...µ

(x)dx

···dx

The space of complex-valued differential forms has thus been made to look like a

collection of 2

Dirac spinor fields, one for each value of the “flavour index” β. These

αβ

are called Kähler–Dirac fields. They are not really flavoured spinors because a

rotation transforms both the α and β indices.

Exercise 15.14: That a set of 2n Dirac γ ’shasa2

-by-2

matrix representation is most

naturally established by using the tools of second quantization. To this end, let a

, a

†

i = 1, ..., n, be set of anticommuting annihilation and creation operators obeying

+ a

= 0, a

†

+ a

†

= δ

15.2 Geometry of SU(2) 551

and let |0 be the “no particle” state for which a

|0=0, i = 1, ..., n. Then the 2

states

, ..., m

=(a

†

)

···(a

†

)

|0,

where the m

take the value 0 or 1, constitute a basis for a space on which the a

and a

†

act irreducibly. Show that the 2n operators

= a

+ a

†

i+n

= i(a

− a

†

obey

+ γ

= 2δ

µν

and hence can be represented by 2

-by-2

matrices. Deduce further that spaces of left

and right chirality are the spaces of odd or even “particle number”.

The adjoint representation

We established the connection between SU(2) and SO(3) by means of a conjugation:

=σ

(→ U=σ

−1

. The idea of obtaining a representation by conjugation works for an

arbitrary Lie group. It is easiest, however, to describe in the case of a matrix group where

we can consider an infinitesimal element I +i

. The conjugate element g(I +i

−1

will also be an infinitesimal element. Since gIg

−1

= I , this means that g(i

−1

must

be expressible as a linear combination of the i

matrices. Consequently, we can define

a linear map acting on the element X = ξ

of the Lie algebra by setting

Ad(g)

≡ g

−1

[

Ad (g)

]

. (15.80)

The matrices with entries

[

Ad (g)

]

form the adjoint representation of the group. The

dimension of the adjoint representation coincides with that of the group manifold.

The spinor construction shows that the defining representation of SO(3) is the adjoint

representation of SU(2).

For a general Lie group, we make Ad(g) act on a vector in the tangent space at the

identity by pushing the vector forward to TG

by left multiplication by g, and then

pushing it back from TG

to TG

by right multiplication by g

−1

Exercise 15.15: Show that

[

Ad (g

)

]

[

Ad (g

)

]

[

Ad (g

)

]

thus confirming that Ad(g) is a representation.

552 15 Lie groups

15.2.6 Peter–Weyl theorem

The volume element constructed in Section 15.2.4 has the feature that it is invariant. In

other words if we have a subset  of the group manifold with volume V , then the image

set g under left multiplication has exactly the same volume. We can also construct a

volume element that is invariant under right multiplication by g, and in general these

will be different. For a group whose manifold is a compact set, however, both left- and

right-invariant volume elements coincide. The resulting measure on the group manifold

is called the Haar measure.

For a compact group, therefore, we can replace the sums over the group elements

that occur in the representation theory of finite groups, by convergent integrals over the

group elements using the invariant Haar measure, which is usually denoted by d[g].

The invariance property is expressed by d[g

g]=d[g] for any constant element g

This allows us to make a change-of-variables transformation, g → g

g, identical to that

which played such an important role in deriving the finite-group theorems. Consequently,

all the results from finite groups, such as the existence of an invariant inner product and

the orthogonality theorems, can be taken over by the simple replacement of a sum by

an integral. In particular, if we normalize the measure so that the volume of the group

manifold is unity, we have the orthogonality relation



d[g]



(g)

∗

(g) =

dim J

. (15.81)

The Peter–Weyl theorem asserts that the representation matrices D

(g) form a com-

plete set of orthogonal functions on the group manifold. In the case of SU(2) this tells

us that the spin J representation matrices

(θ, φ, ψ) =J , m|e

−iJ

|J , n,

= e

−imφ

(θ)e

−inψ

, (15.82)

which you will likely have seen in quantum mechanics courses,

are a complete set of

functions on the 3-sphere with orthogonality relation

16π



sin θdθ



2π

dφ



4π

dψ



(θ, φ, ψ)

∗



(θ, φ, ψ)

2J + 1



. (15.83)

Since the D

(where L has to be an integer for n = 0 to be possible) are independent of

the third Euler angle, ψ, we can do the trivial integral over ψ to obtain the special case

4π



sin θdθ



2π

dφ



(θ, φ)

∗



(θ, φ) =

2L + 1



. (15.84)

See, for example, G. Baym, Lectures on Quantum Mechanics, Chapter 17.

15.2 Geometry of SU(2) 553

Comparing with the definition of the spherical harmonics, we see that we can identify

(θ, φ) =

2L + 1

4π



(θ, φ, ψ)

∗

. (15.85)

The complex conjugation is necessary here because D

(θ, φ, ψ) ∝ e

−imφ

, while

(θ, φ) ∝ e

imφ

The character, χ

(g) =

(g), will be a function only of the rotation angle θ and

not the axis of rotation – all rotations through a common angle being conjugate to one

another. Because of this, χ

(θ) can be found most simply by looking at rotations about

the z-axis, since these give rise to easily computed diagonal matrices. Thus, we find

χ(θ) = e

iJ θ

+ e

i(J −1)θ

+···+e

−i(J −1)θ

+ e

−iJ θ

sin(2J + 1)θ/2

sin θ/2

. (15.86)

Warning: The angle θ in this formula and the next is not the Euler angle.

For integer J , corresponding to non-spinor rotations, a rotation through an angle θ

about an axis n and a rotation though an angle 2π −θ about −n are the same operation.

The maximum rotation angle is therefore π. For spinor rotations this equivalence does

not hold, and the rotation angle θ runs from 0 to 2π . The character orthogonality relation

must therefore be



2π

(θ)χ



(θ) sin

(θ/2)dθ = δ



, (15.87)

implying that the volume fraction of the rotation group containing rotations through

angles between θ and θ + dθ is sin

(θ/2)dθ/π.

Exercise 15.16: Prove this last statement about the volume of the equivalence classes

by showing that the volume of the unit 3-sphere that lies between a rotation angle of θ

and θ + dθ is 2π sin

(θ/2)dθ.

15.2.7 Lie brackets vs. commutators

There is an irritating minus-sign problem that needs to be acknowledged. The Lie bracket

[X , Y ] of two vector fields is defined by first running along X , then Y and then back in

the reverse order. If we do this for the action of matrices,

X and

Y , on a vector space,

then, since the sequence of matrix operations is to be read from right to left, we have

−t

= I − t

[

X ,

Y ]+···, (15.88)

554 15 Lie groups

which has the other sign. Consider, for example, rotations about the x, y, z axes, and look

at the effect these have on the coordinates of a point:



δy =−z δθ

δz =+y δθ



=⇒ L

= y∂

− z∂

⎛

⎝

00 0

00−1

01 0

⎞

⎠



δz =−x δθ

δx =+z δθ



=⇒ L

= z∂

− x∂

⎛

⎝

001

000

−100

⎞

⎠



δx =−y δθ

δy =+x δθ



=⇒ L

= x∂

− y∂

⎛

⎝

0 −10

100

000

⎞

⎠

From this we find

, L

]=−L

, (15.89)

as a Lie bracket of vector fields, but

[

]=+

, (15.90)

as a commutator of matrices. This is the reason why it is the left-invariant vector fields

whose Lie bracket coincides with the commutator of the i

matrices.

Some insight into all this can be had by considering the action of the left-invariant

fields on the representation matrices, D

(g). For example,

(g) = lim

→0







(g(1 + i

)) − D

(g)



= lim

→0









(g)D



(1 + i

) − D

(g)



= lim

→0









(g)(δ



+ i(



)



) − D

(g)



= D



(g)(i



)



, (15.91)

where



is the matrix representing

in the representation J . Repeating this exercise

we find that



(g)

= D



(g)(i



)







)



. (15.92)

Thus

, L

(g) = D



(g)[i



, i



]



, (15.93)