Сундарон Э.М. Выборочный контроль

Подождите немного. Документ загружается.

партию и перемешивают. Затем берут наугад второе изде-

лие, производят те же самые операции и т.д. Вероятность

извлечения (n-d) годных изделий из проконтролированных

определяются по формуле

ddn

dnd

ddndn

nndn

qpqpCр

−

−−

−

== ***

)!!*(

(8)

Математическое ожидание

µ и дисперсию σ

биноми-

ального распределения находят по формулам:

nq=

(9)

nqp=

. (10)

Закон редких событий (Пуассона). Закон редких со-

бытий применяется в машиностроении для выборочного

контроля готовой продукции, когда по техническим усло-

виям в принимаемой партии продукции допускается неко-

торый процент брака (обычно небольшой) - q<<0,1.

Если вероятность q события А очень мала (q

≤0,1), а

число испытаний велико, то вероятность того, что событие

А наступит d раз в n испытаниях, будет равна

ednp

−

= *),(

, (11)

где а=nq=

µ[m] - математическое ожидание случайной ве-

личины.

Уравнение (11) определяет собой распределение ред-

ких событий, или распределение Пуассона.

Когда число испытаний n велико, а q мало, то закон

биномиального распределения и закон редких событий

практически совпадают. Это имеет место тогда, когда

≤0,1. При этих условиях вместо формулы (8) можно при-

менить формулу (11).

Принимая а=nq, формула (7) примет вид:

ednр

−

= *),(

)(

. (12)

При помощи закона редких событий можно вычис-

лить вероятность того, что в выборке из n единиц будет со-

держаться: 0,1,2,3, и т.д. бракованных деталей, т.е. задан-

ное d раз. Можно также вычислить вероятность появления

в такой выборке d штук дефектных деталей и более. Эта

вероятность на основании правила сложения вероятностей

будет равна

∑∑

−

−=−=

1),(1),(

eXnPdnP

(13)

Пример 1. В партии имеются бракованные детали,

доля которых составляет 0,1. Последовательно берут 10

деталей и обследуют, после чего их возвращают в партию,

т.е. испытания носят независимый характер. Какова веро-

ятность того, что при проверке 10 деталей попадется одна

бракованная?

Решение. Из условия задачи q=0,1 n=10 d=1.

Очевидно, что р=1-q=0,9. Тогда

387,09,0*1,0*)1;10(

9,0

!9!1

==Р

Полученный результат можно отнести и к тому слу-

чаю, когда извлекается подряд 10 деталей без возврата их

обратно в партию. При достаточно большой партии, на-

пример, 1000 шт., вероятность извлечения деталей изме-

нится ничтожно мало. Поэтому при таких условиях извле-

чение бракованной детали можно рассматривать как собы-

тие, не зависящее от результатов предшествующих испы-

таний.

Пример 2. В партии имеется 1% бракованных дета-

лей. Какова вероятность того, что при взятии из партии

выборки объемом 50 единиц продукции в ней будет нахо-

диться 0,1,2,3,4 дефектные детали.

Здесь q=0.01, nq=50*0.01=0.5

607,0*)0;50(

5,0

−

еР

303,0*)1;50(

5,0

−

еР

075,0*)2;50(

5,0

−

еР

012,0*)3;50(

5,0

−

еР

001,0*)4;50(

5,0

−

еР

Порядок работы:

1. Ознакомиться с общими положениями методиче-

ских указаний, обратив внимание на примеры и методики

решения задач.

Решить задачи 1 и 2 по данным, приведенным в

таблицах 1и 2 приложения 2.

Номер варианта выбирается по последней цифре

шифра зачетной книги.

3. Оформить отчет и ответить на контрольные во-

просы.

Задание 1. По данным, приведенным в таблице 1 при-

ложения 2, при заданной браковочной доле определить

вероятность того, что в выборке с возвратом среди n про-

контролированных изделий окажется d дефектных изде-

лий.

Задание 2. По данным, приведенным в таблице 2 при-

ложения 2 при известных значениях доли дефектных изде-

лий в партии D, объема выборки n, определите вероятности

появления d дефектных изделий в выборке.

Контрольные вопросы

1 Какие основные законы применяются при контроле

качества по альтернативному признаку?

2 Изобразить графики нормального, гипергеометри-

ческого, биномиального законов распределения вероятно-

сти и график закона распределения вероятности Пуассона.

Описать способ выражения законов распределения веро-

ятности в виде формул.

3 Какому закону распределения вероятности подчи-

няются результаты контроля выборки без возврата, выбор-

ки с возвратом?

4 Какой закон распределения применяется в случае

очень малой вероятности события?

Практическое занятие 3

Правила переключения планов приемочного

контроля

Общие положения: Основной задачей при прове-

дении выборочного приемочного контроля является опре-

деление оптимального плана контроля.

Под планом контроля понимают совокупность значе-

ний объемов выборок n, приемочных и браковочных чисел.

При выборе плана контроля следует определить его

кодовое обозначение, для чего в свою очередь устанавли-

вается объем партий, представляемых на контроль, а также

степень контроля.

В нормативной документации по статистическим ме-

тодам контроля предусмотрены семь степеней контроля:

четыре специальных (С-1. С-2, С-3, С-4) и три общих (I, II,

III).

Основной для применения является степень контроля

II.

Общую степень контроля I следует применять в тех

случаях, когда проведение контроля связано со значитель-

ными затратами или потери от принятия партий с большим

количеством дефектных изделий сравнительно невелики.

Общую степень контроля III следует применять в тех

случаях, когда затраты на контроль сравнительно невелики

или требуется тщательный контроль партий продукции.

Специальные степени контроля применяют в тех слу-

чаях, когда целесообразен контроль малых выборок и до-

пустимы большие риски потребителя, например, в случае

разрушающего контроля. Риски потребителя и изготовите-

ля при применении специальных степеней контроля следу-

ет оценивать с помощью оперативных характеристик.

На каждом уровне контроля следует применять пра-

вила переключения, требующие перехода на нормальный,

усиленный и ослабленный контроль в соответствии с

ГОСТ Р 50779.71-99.

На начальном этапе контроля, если не оговорены осо-

бые условия, устанавливается нормальный контроль.

Нормальный, усиленный или ослабленный контроль

должен продолжаться без изменения до тех пор, пока не

будут выполнены переключения. Процедуры переключе-

ния применяют для каждого класса несоответствий или не-

соответствующих единиц продукции отдельно.

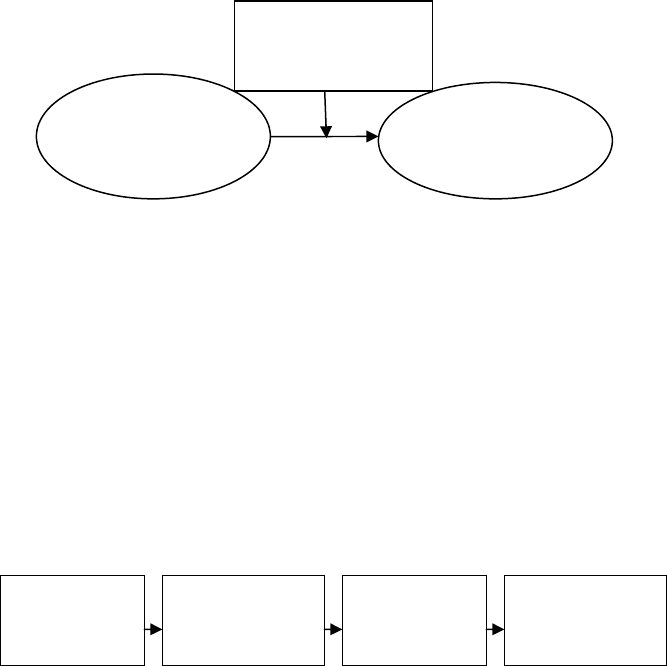
Процедуры и правила переключения представлены на

рис. 4.

Рис. 4 – Схема правил переключения

Если общее число партий, не принятых с первого

предъявления, в серии последовательных партий на уси-

ленном контроле, достигает пяти, то процедуры приемки

должны быть приостановлены. Контроль партий по выбо-

рочным планам не возобновляют до тех пор, пока постав-

щик не примет меры по улучшению качества поставляемой

продукции или услуг. Контроль партий должен быть во-

зобновлен на усиленном контроле.

Пример 1. На предприятии машиностроительной от-

расли проводится выборочный приемочный контроль по

альтернативному признаку.

Задание

1. Выбрать объект, контролируемый по альтернатив-

ному признаку. Самим задать исходные данные (объем

контролируемой партии N, допускаемый процент брако-

ванных изделий в партии

ген,

%, объем выборки, требова-

ния к общему числу несоответствующих единиц продук-

ции, а также дополнительные условия относительно ста-

бильности и устойчивости производства).

2. Сформулировать условие задачи и правило приня-

тия решения по результатам контроля.

3. Смоделировать данные контроля качества по аль-

тернативному признаку. Данные занести в таблицу 2.

Таблица 2

N q

ген,

Номер

пар-

тии

Объем

выбор-

ки

Кол-во

бракован-

ных изде-

лий

Решение о при-

нятии (непри-

нятии) партии

Примечание

4. По результатам контроля в соответствии с ГОСТ Р

50779.71-99 принять решение о переходе (или непереходе)

к другой степени контроля.

5. Результат переключения представить в виде схемы:

6. После переключения на ослабленную или усилен-

ную степень контроля снова смоделировать данные ре-

зультатов контроля и заполнить таблицу 2.

7. п.п.4,5 и 6 повторить несколько раз таким образом,

чтобы в работе были использованы все степени контроля

(нормальный, ослабленный, усиленный, а также и возмож-

ное прекращение выборочного приемочного контроля, и

переход к сплошному контролю) с обоснованием выбран-

ного переключения.

8. Результаты работы представьте в виде окончатель-

ной схемы с последовательностью уровней контроля (при-

мер схемы приводится на рис.5).

Рис.5

9. Разработанную схему переключений привести в со-

ответствие со схемой ГОСТ Р 50779.71-99.

Нормальный

уровень кон-

троля

Ослабленный

уровень кон-

троля

Нормальный

уровень

кон-

троля

Усиленный

уровень кон-

троля

Нормальный

ур

овень конт

о-

Здесь указать ус-

ловия выбранного

переключения

Контрольные вопросы

1 В каком случае необходимо прекратить выбороч-

ный и перейти к сплошному контролю качества?

2 Какая степень контроля применяется на началь-

ных этапах организации выборочного приемочного кон-

троля?

3 В результате прекращения выборочного контроля

и перехода к сплошному контролю поставщик не имеет

права применять выборочный контроль качества до тех пор

пока им не будут приняты меры по улучшению качества

поставляемой продукции (услуг) и уполномоченная сторо-

на не признает эти меры эффективными. Если эти условия

будут выполнены, то выборочный контроль может быть

возобновлен. С какой степени контроля в этом случае мо-

жет быть возобновлен выборочный приемочный контроль?

Практическая работа 4

Разработка плана контроля по альтернативному

признаку.

Общие положения:

Несоответствующая единица продукции: единица

продукции или услуга, содержащая, по крайней мере одно

несоответствие. Несоответствующие единицы продукции в

зависимости от значимости подразделяют на следующие

классы:

А – единица продукции, содержащая одно или более

несоответствий типии А, может также содержать несоот-

ветствия типа В и (или) С.

В - единица продукции, содержащая одно или более

несоответствий типии В, может также содержать несоот-

ветствия типа С, но не имеет несоответствий типа А.

Процент несоответствующих единиц продукции:

отношение числа несоответствующих единиц продукции к

общему числу единиц продукции, умноженное на 100.

Процент число несоответствующих

Несоответствующих = единиц продукции

х 100

единиц продукции общее число единиц

продукции

Число несоответствий на 100 единиц продукции

произведение частного от деления числа несоответствий на

общее число единиц продукции и 100

Число

несоответствий = число несоответствий

_ х 100

на 100 единиц общее число единиц

продукции продукции

Приемлемый уровень качества (AQL): при рас-

смотрении непрерывной последовательности партий уро-

вень качества, который является границей удовлетвори-

тельного среднего уровня качества процесса.

План выборочного контроля (выборочный план):

определенный план контроля, который устанавливает чис-

ло единиц продукции из каждой партии, подлежащие кон-

тролю (объем выборки или объемы серий выборок) и необ-

ходимые критерии приемлемости партии (приемочные и

браковочные числа).

Схема выборочного контроля (выборочная схема):

сочетание выборочных планов контроля и правил пере-

ключения.

Система выборочного контроля (выборочная сис-

тема): совокупность выборочных планов или схем с уче-

том объемов партий, уровней контроля и приемлемого

уровня качества AQL.

Виды выборочных систем: выборочная система для

планов контроля на основе предельного качества LQ

(ГОСТ Р 50779.72)

Определение плана контроля по альтернативному

признаку производится согласно ГОСТ Р 50779.71-99.

Под планом выборочного контроля подразумевается

совокупность данных, устанавливающих объем выборки,

подлежащий контролю, и необходимые критерии прием-

лемости партии (приемочные и браковочные числа).

Задание 1. На предприятии машиностроительной от-

расли производится одноступенчатый контроль качества

изделия по альтернативному признаку. Определите план

контроля партии объемом N для нормального, ослабленно-

го и усиленного степеней контроля, при условии, что из-

вестны результаты сплошного контроля (количество де-

фектных изделий D

, D

в партиях объемами N

, N

соответственно.) Исходные данные приведены в приложе-

нии В (вариант выбирать по последним двум цифрам за-

четной книжки).

Результаты работы занесите в таблицу 3

Таблица 3

Крите-

рии при-

емки

Вариант

Уровень контроля

Приемлемый уро-

вень качества

Объем контроли-

руемой партии N

Степень кон-

троля

Код объема вы-

бо

ки

Объем выборки n

нормальный

усиленный

ослабленный

Задание 2. На предприятии машиностроительной

отрасли производится двухступенчатый контроль качества

изделия по альтернативному признаку. По данным задания

1 определите план контроля партии изделий объемом N

для нормального, ослабленного и усиленного степеней

контроля. Результаты работы занесите в таблицу 4.

Задание 3. По результатам работы сделать вывод об

изменении плана контроля при переходе от одной степени

контроля к другой, а также при изменении типа контроля с

одноступенчатого на двухступенчатый.

Таблица 4

Объем

выбор-

ки

Критерии приемки

первой

выборки

второй

выборки

Вариант

Уровень контроля

Приемлемый уровень ка-

чества

Объем контролируемой

партии N

Степень

контроля

Код объема выборки

нормаль-

ный

усиленный

ослаблен-

ный

Контрольные вопросы

1 Дать определение понятию «контроль качества по

альтернативному признаку». Привести 5 примеров контро-

ля качества по альтернативному признаку.

2 Каким законам распределения подчиняются ре-

зультаты контроля по альтернативному признаку.

3 Дать определение понятию «план выборочного

контроля».

4 Какая характеристика является оценкой эффек-

тивности плана выборочного контроля?

5 Какие факторы необходимо учитывать при выборе

уровня контроля при контроле по альтернативному при-

знаку?

6 Какие факторы необходимо учитывать при выборе

типа плана контроля при контроле по альтернативному

признаку?

7 Проанализировать планы выборочного контроля

при одноступенчатом, двухступенчатом и многоступенча-

том типах контроля и сделать вывод об изменениях плана

контроля при переходе от одного к другому типу контроля.

Практическая работа 5

Контроль по количественному признаку

Общие положения.

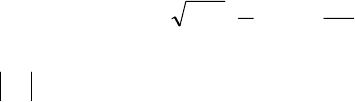
Алгоритм разработки плана контроля, проводимого

поставщиком, представлен на рис. 6.

Анализ установленных технических требований к продукции

Односторонний допуск Двусторонний

допуск

Установлено

наименьшее

предельное

значение

показателя

{у≥а}

Установлено

наибольшее

предельное

значение

показателя

{у≤в}

Установлены

наименьшее и

наибольшее

значения

показателя

{а≤у≤в}

Получение априорной информации (µ, σ) по результатам пред-

варительного сплошного контроля

Установление приемочных границ

{у≥а} {у≤в} {а≤у≤в}

НПГ ВПГ НПГ ВПГ НПГ ВПГ

а+К

σ - - в-К

σ а+К

σ в-К

Рис. 6

Порядок работы:

Ознакомиться с общими положениями

методических указаний, а также государственного

стандарта ГОСТ Р 50779.53-98 «Приемочный контроль

качества по количественному признаку для нормального

закона распределения. Часть 1. Стандартное отклонение

известно.

Определение репрезентативного объема выборки n по значению

минимального запаса качества g и NQL,%

{у≥а} {у≤в} {а≤у≤в}

g=(µ-а)/σ g=(в-µ)/σ g=min {(µ-а)/σ;

(в-µ)/σ}

Установление нормативного значения риска потребителя β

(степень доверия Т)

Определение значения коэффициента К

при заданных:

(Т) и NQL,%

Правило принятия решения

По результатам анализа общих положений

стандарта разработать алгоритм плана приемочного

контроля, проводимого потребителем (аналогично

представленному алгоритму на рис.6).

По вариантам, представленным в таблице 4, и по

предложенным данным решите практические задачи 1-3.

По результатам решения задач сформулируйте

выводы.

Оформите работу и ответьте на контрольные во-

просы.

Задача 1: Требования в технической документации

поставщика на изделие сформулированы в виде

А ± ∆А. По

результатам сплошного контроля априорная информация

содержит сведения о

µ и σ. Разработать планы выборочно-

го приемочного контроля поставщика и потребителя, если

организацией-поставщиком получен сертификат соответ-

ствия СМК международным стандартам.

Задача 2: Разработать планы приемочного контроля

поставщика и потребителя при различных степенях дове-

рия Т, исключая соответственно степени Т

и Т

Задача 3: По результатам решения задач 1 и 2 по-

строить графики зависимости элементов плана контроля (n,

g, НПГ и ВПГ) от степени доверия Т.

Таблица 4

Вариант 1 2 3 4 5 6 7

А 11,9 10 17 15 25 15 19

∆А

0,05 0,2 0,3 0,3 0,3 0,3 0,2

11,80 10,07 16,99 14,98 24,42 15,0 18,99

0,10 0,12 0,09 0,09 0,11 0,10 0,1

Вариант 8 9 10 11 12 13 14

А 13 8 16 45 20 10 15

∆А

0,1 0,4 0,6 0,3 0,3 0,3 0,2

12,8 7,98 16,1 44,95 19,42 10,0 14,99

0,07 0,12 0,15 0,13 0,11 0,10 0,10

Контрольные вопросы

1 Сформулировать сущность выборочного контроля

по количественному признаку.

2 Пояснить, почему контроль по количественному

признаку обладает более высокой информативностью, чем

контроль по альтернативному признаку.

3 Какую вероятность приемки партий обеспечивают

планы контроля по ГОСТ Р 50779.53-98.

ПРИЛОЖЕНИЕ 1

Биномиальные коэффициенты

()

∑

−

knkk

baCba

Свойства коэффициентов

C 2

∑

;

−

CCC

1 −

−

Треугольник Паскаля:

С 1

С 1 1

С 1 2 1

С 1 3 3 1

C 1 4 6 4 1

……….. ………..

Здесь каждое число кроме крайних единиц является сум-

мой двух вышерасположенных.

Формула Стерлинга

























12! ,

где

12/1≤

, а 718.2

≈

e - основание натурального ло-

гарифма.

ПРИЛОЖЕНИЕ 2

Таблица 1

N вар-та q n d

1 0,05 10 1

2 0,05 10 2

3 0,05 10 3

4 0,05 10 4

5 0,05 10 5

6 0,1 10 6

7 0,1 10 7

8 0,1 10 8

9 0,1 10 9

10 0,1 10 10

11 0,15 15 1

12 0,15 15 2

13 0,15 15 3

14 0,15 15 4

15 0,15 15 5

16 0,2 15 6

17 0,2 15 7

18 0,2 15 8

19 0,2 15 9

20 0,2 15 10

Таблица 2

N вар-та q n d

1 0,05 20 5,6,7,8,

2 0,07 30 4,5,6,7

3 0,09 40 0,1,2,3

4 0,11 50 6,7,8,9

5 0,13 60 5,6,7,8

6 0,15 70 4,5,6,7

7 0,17 80 0,1,2,3

8 0,19 90 1,2,3,4

9 0,21 100 2,3,4,5

10 0,23 120 3,4,5,6

11 0,25 140 4,5,6,7

12 0,27 160 0,1,2,3

13 0,29 180 1,2,3,4

N вар-та q n d

14 0,31 200 2,3,4,5

15 0,33 125 3,4,5,6

16 0,35 145 4,5,6,7

17 0,37 155 0,1,2,3

18 0,39 175 1,2,3,4

19 0,41 185 2,3,4,5

20 0,43 195 3,4,5,6

Таблица 3

Вариант N

01 1000 900 1500 9 5 12 1200

02 700 500 1400 5 10 17 3200

03 500 1600 1100 1 15 10 1400

04 2000 1900 1700 18 15 14 2500

05 2000 1800 3000 18 10 24 2000

06 1200 1000 2000 10 7 15 1700

07 600 450 750 5 3 7 500

08 2000 2200 1800 15 16 10 1500

09 1000 1500 2000 15 2 10 1900

10 800 500 300 7 4 2 400

11 1200 800 300 11 7 5 500

12 1000 800 500 6 10 15 1500

13 700 1000 1200 6 10 9 1500

14 1200 1000 750 7 9 14 1200

15 2000 800 600 6 10 9 1500

16 2100 2000 2600 13 9 16 2000

17 1000 1200 1100 10 9 9 1000

18 1500 1400 1200 5 6 5 1100

19 1900 1700 1600 6 7 4 1500

20 2000 1800 2100 6 8 10 1900

Подписано в печать 24.11.2006г. Формат 60×84

1/16. Усл. п.л. 2,4. Тираж 100 экз. Заказ № 249.

___________________________________________

Издательство ВСГТУ. г. Улан-Удэ, ул. Ключевская, 40, В.