Tabak J. Beyond Geometry: A New Mathematics of Space and Form

Подождите немного. Документ загружается.

10 BEYOND GEOMETRY

the same will often appear superficially to be very different. Our

visual imagination is often of little use in determining topological

equivalence.

The Beginnings of Calculus

To appreciate some of the motivations for creating topology, it

helps to understand some of the logical shortcomings in early

conceptions of calculus. The German mathematician Gottfried

Leibniz (1646–1716) created calculus. (Isaac Newton discov-

ered calculus independently of Leibniz, and his formulation of

calculus had the same sorts of logical shortcomings as those of

Leibniz. Only Leibniz’s contribution is considered here, because

in addition to calculus, Leibniz also speculated on the possibilities

inherent in a geometry that was independent of the idea of mea-

surement. He called it analysis situs, and analysis situs became the

forerunner of topology.)

Leibniz spoke several languages. In addition, he was a legal

scholar, a philosopher, a diplomat, an inventor, a scientist, and

a mathematician. He is best remembered, as mentioned above,

as the codiscoverer of calculus, but he also made many other

mathematical discoveries, including the binary number system,

which had no apparent use until the invention of the computer.

He invented one of the earliest mechanical calculators, and he was

a writer who simultaneously maintained lively correspondences

with hundreds of people. He is sometimes described as the last

completely educated European in the sense that he is often cred-

ited with being the last person to attain a high level of expertise in

every academic discipline known during his time.

Leibniz expressed his ideas about calculus in the language of

geometry. One problem to which he gave a great deal of thought

involved finding the slope of the line tangent to a given curve at a

given point. (Recall that a line that is tangent to a curve at a par-

ticular point is the best straight line approximation to the curve at

that point.) See the accompanying diagram. The problem of find-

ing a tangent may sound too abstract to be useful, but historically

it is one of the most important problems in mathematics. In fact,

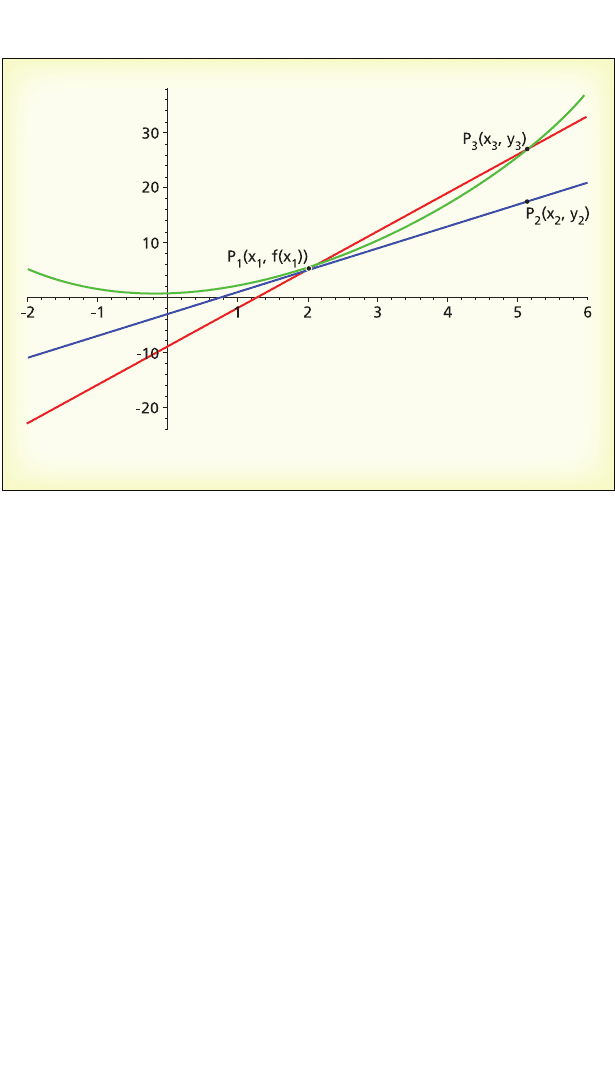
Topology: A Prehistory 11

the problem and its solution lie at the very heart of calculus, and

the ability to compute the tangent has many applications to prob-

lems in engineering and science as well as mathematics.

As is indicated in Euclid’s first postulate, a line is determined

when any two points on the line are known. If Leibniz could find

two points on the tangent line—say and P

, y

) and P

, y

)—he

would also know the slope of the line according to the following

formula:

(2.1) slope =

− y

———

− x

(Here P

and P

are the names of the points on the tangent line,

and (x

, y

) and (x

, y

) are the coordinates of the points P

and P

respectively. Formula (2.1) is discussed at length in every high

school algebra and trigonometry class.)

The red line is a secant line, and the blue line is the line tangent to the

curve at the point P

. The tangent is determined by, for example, P

and

, but the coordinates of P

are unknown. If P

is used instead, then, as

the distance between P

and P

approaches zero, the slope of the secant line

approaches the slope of the tangent line.

12 BEYOND GEOMETRY

Leibniz’s problem was that he only knew P

, the point on the

curve through which the tangent passes. He did not know P

nor did he have a way of finding P

, and he could not determine

the tangent from knowledge of P

alone. He could, however,

approximate the unknown tangent by choosing another point on

the curve—in the diagram that point is labeled P

, y

)—and by

employing formula (2.1) with (x

, y

) written in place of (x

, y

From P

he could compute an approximation to the slope of the

tangent line. (The line determined by P

and P

is called a secant

line, or secant for short.) The quality of the approximation one

obtains by using P

and P

instead of P

and P

is determined by the

choice of P

. If P

is close to P

, the difference between the slope of

the secant and the slope of the tangent will be small, and the closer

is to P

, the smaller the difference will be.

It might be tempting to think that because the slope of the

secant approaches the slope of the tangent as P

approaches P

along the curve, the slope of the secant equals the slope of the

tangent when P

finally “gets to” P

. But this idea cannot be right.

When P

coincides with P

, the secant fails to exist. This is reflect-

ed in the formula for the slope: When P

coincides with P

—and

, y

) coincides with (x

, y

)—the formula for the slope becomes

meaningless since the denominator is zero, and division by zero

has no meaning. As a general rule, there is no choice for P

on the

curve that will yield the slope of the tangent.

It would be hard to overstate the mathematical problems

caused by these simple-sounding observations. In attempting to

overcome these mathematical difficulties, Leibniz postulated the

existence of a class of numbers that he sometimes called infini-

tesimals; other times he called them differentials. He imagined

them as being greater than zero but smaller than any positive

number. They were so small that no matter how many were

added together, their sum was still less than any positive num-

ber. He often tried to explain the concept of differentials by way

of analogy. He wrote, “. . . the differential of a quantity can be

thought of as bearing to the quantity itself a relationship analo-

gous to that of a point to the earth or of earth’s radius to that of

the heavens.”

Topology: A Prehistory 13

Leibniz represented an infinitesimal in the y-direction with the

symbol dy and an infinitesimal in the x-direction with the symbol

dx. By adding dx to x

and dy to y

, Leibniz obtained the point

+ dx, y

+ dy), which he envisioned as a point on the curve

very close to P

—Leibniz used the phrase “infinitely close” to P

In fact, according to Leibniz, P

, y

) and P

+ dx, y

+ dy) were

so close that the difference between the two points was “less than

any given length.” Leibniz described differentials in these words:

“. . . these dx and dy are taken to be infinitely small, or the two

points on the curve are understood to be at a distance apart less

than any given length . . .”

In a sense, P

+ dx, y

+ dy) is the point on the curve that was

immediately adjacent to P

, y

). It is, in effect, the next point

over.

Using formula (2.1) to compute the slope determined by P

, y

)

and P

+ dx, y

+ dy) gives

(2.2) slope =

+ dy − y

—————

+ dx − x

or, upon simplification

(2.3) slope =

—

(The algorithms Leibniz used to manipulate his infinitesimals in

order to obtain numerical answers are omitted here.) The slope

of the tangent line at P

, y

) is better known as the derivative of

the curve at P

, y

). The derivative is a function. Its value at the

point x

is the slope of the tangent line passing through (x

, y

Keep in mind that according to Leibniz, dx is not zero.

Consequently, the denominator of the fraction in equation (2.3)

makes mathematical sense (provided one is willing to accept the

existence of infinitely small nonzero quantities), and the numera-

tor in (2.3) will have approximately the same magnitude as the

14 BEYOND GEOMETRY

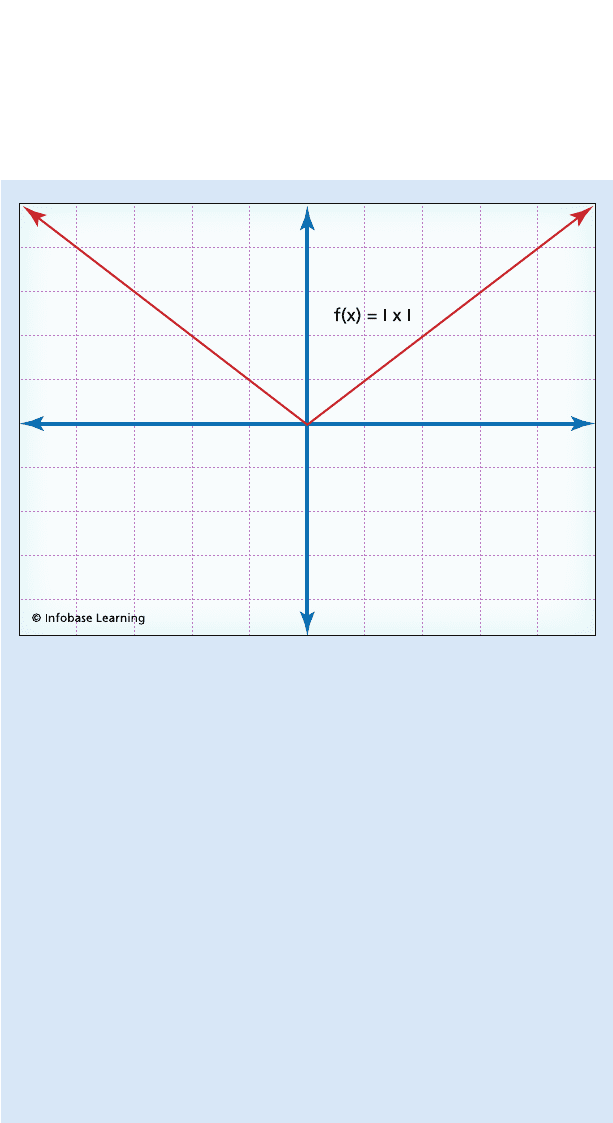
counterexample 1: a continuous function

that is not everywhere differentiable

The mathematicians of Leibniz’s time took it for granted that one could

find a tangent line at every point of a curve. Given a curve and a point

on the curve, the tangent line can be constructed by passing a line

through P

and another point P

lying on the curve. Any point P

differ-

ent from P

will yield a line because any two points determine a line. To

obtain the tangent, according to Leibniz, just allow P

to move “near

enough” to P

. The result, Leibniz asserted, had to be the tangent. This

idea was formulated in terms of a general principle, which is now known

as Leibniz’s principle of continuity:

“In any supposed transition, ending in a terminus, it is permis-

sible to institute a general reasoning, in which the final terminus

may also be included.”

However, this is false, as the following counterexample demonstrates.

Consider the function f(x) = |x|, where the symbol |x| means the “abso-

lute value of x.” (As a matter of definition, |x| = x if x ≥ 0, and |x| = −x if

x < 0.) As is indicated in the accompanying diagram, the graph of this

function lies in the first and second quadrants of the plane. The graph of

f(x) coincides with the graph of the line y = x in the first quadrant, and

in the second quadrant, it coincides with the graph of the line y = −x.

For each positive value of x, the tangent to the graph exists and coin-

cides with the line y = x, and for each negative value of x, the tangent

to the graph exists and coincides with the line y = −x. According to

Leibniz’s principle of continuity, it should be possible to extend to the

origin the process of forming the tangent. The origin would be the “ter-

minus,” but if the origin is approached from the right, the tangent at the

origin must have a slope coinciding with the line y = x—that is, the slope

must be +1. If the origin is approached from the left, the slope of the

tangent at the origin must coincide with the line y = −x—that is, the slope

must be −1. The tangent at the origin is, therefore, impossible to define

since it cannot simultaneously have a slope of +1 and −1. Leibniz’s

principle of continuity fails. There are points on some curves where the

derivative fails to exist.

denominator, so their ratio “makes sense.” Consequently, the

value of the ratio in equation (2.3), which is the value of Leibniz’s

derivative, is determined by the relative sizes of the two infinitesi-

Topology: A Prehistory 15

mals. Finally, because P

, y

) and P

+ dx, y

+ dy) are “infi-

nitely close” together, the slope determined by these two points

must, according to Leibniz, be the slope of the tangent. Why?

Mathematicians soon discovered many examples of functions with the

occasional corner or cusp in their graph. At these points, the derivative

failed to exist. The existence of such curves became geometrically “obvi-

ous” to them (as they become obvious to us) after a little thought. These

mathematicians also believed that it was “obvious” that points where the

derivative fails to exist are exceptional, in the sense that cusps and cor-

ners are “always” isolated from each other, and therein lies the problem

with geometric reasoning. While it is hard to imagine a curve that is so

“jagged” that it consists entirely of cusps and corners, such curves are

more the rule than the exception. Geometric reasoning failed to reveal

the existence of continuous nowhere differentiable functions because

most of us cannot imagine what such jagged curves look like. Certainly

their graphs cannot be drawn. Topological ideas would be required

before calculus could be put on a firm logical foundation.

The derivative is equal to +1 at every point on the curve that lies in

the first quadrant, and the derivative is equal to −1 at every point on

the curve that lies in the second quadrant. At the origin, therefore, the

derivative does not exist.

16 BEYOND GEOMETRY

The (positive) difference between the slope of the secant and the

slope of the tangent must be less than any given number because

the two points are at a distance apart that is “less than any given

length.” This was the key: By choosing P

“infinitely close” to P

the slope of the resulting line equaled the slope of the tangent.

For Leibniz, infinitesimals were a convenient quasi-mathemati-

cal idea that enabled him to give expression to the very important

mathematical idea of closeness. Calculus, as envisioned by Leibniz

(and Newton), was not a sequence of logical deductions beginning

from a set of axioms and definitions. It was not mathematics in the

sense that the Greeks understood the word. Calculus was originally

a set of techniques the justification for which was the results that

were obtained by using them. Calculus made a huge difference in

the progress of science and

mathematics right from the

time of its introduction, but

even early in the development

of calculus its logical short-

comings were apparent to

many. The British philosopher

and theologian Bishop George

Berkeley (1685–1753) famous-

ly criticized the foundations

of calculus when he wrote, “I

say that in every other science

men prove their conclusions

by their principles and not

their principles by their con-

clusions.” Unfortunately, it is

often easier to recognize an

error than to fix one.

Without a logical framework

to support his algorithms,

Leibniz was unable to rigor-

ously test his ideas. In retro-

spect, some of his ideas were

correct, some were incorrect,

Bishop George Berkeley. Calculus

was originally expressed as a

collection of algorithms unsupported

by careful mathematical reasoning.

Berkeley famously mocked the

mathematicians of his time for

“proving . . . their principles

by their conclusions.”

(National

Portrait Gallery)

Topology: A Prehistory 17

and in some cases it is not quite clear what he meant. He was

not alone. A rigorous understanding of the mathematical idea of

closeness—an understanding that does not make use of infinitesi-

mals—eluded mathematicians until well into the 19th century. By

the latter half of the 19th century, mathematicians were forced to

develop new ideas because the old ad hoc justifications proposed

by Leibniz, Newton, and their successors, ideas that had once

spurred progress in mathematics and science, had become a hin-

drance to further progress.

a failure of intuition

For millennia, Greek geometry occupied a central place in the

mathematical traditions of many cultures. Early mathemati-

cians—some lived in present-day Turkey, present-day Iran and

Iraq, North Africa, and southern Europe—regarded Greek geom-

etry with a sort of reverence. They believed that there was little

they could add to the study of geometry because the Greeks had

already accomplished the better part of what could be done. The

Greeks had, of course, left some problems unsolved, and later gen-

erations of mathematicians addressed themselves to these prob-

lems. Even so, for more than 2,000 years, mathematicians could

not imagine a geometry other than the geometry of Euclid. They

could not imagine another model for space than the one described

in Euclid’s Elements. Part of this chapter describes how, early in the

19th century, this concept of geometry was finally abandoned, and

mathematicians began to consider so-called non-Euclidean geom-

etries. For these mathematical pioneers, the new geometries did

not have the same intuitive appeal as did Euclid’s. In fact, the first

mathematician to publish a description of a non-Euclidean geom-

etry described his discovery as an “imaginary” geometry to distin-

guish it from what he perceived as the real geometry of the ancient

Greeks. Nevertheless, the willingness to propose alternative sets

of geometric axioms was an enormous conceptual breakthrough

that prepared the way for early topologists, who often spent a

great deal of time tinkering with alternative sets of topological

axioms in order to generate “spaces” with various properties.

The second part of this chapter concerns an important attempt

to correct the logical shortcomings in Leibniz’s (and Newton’s)

A Failure of Intuition 19

intuitive conceptions of cal-

culus. The substitution of

logic for pictures is called

the arithmetization of analy-

sis. (Analysis is the branch of

mathematics that grew out of

calculus.) The drive to place

analysis on a firm logical foun-

dation also began in earnest in

the early decades of the 19th

century. As described in chap-

ter 1, calculus was initially

justified in two ways: first,

by appealing to one’s intu-

ition about the existence of

various limits and second by

pointing to the important and

often correct results obtained

by using calculus algorithms.

The problem is that in calcu-

lus, as in the rest of mathematics, intuition is often a poor guide

to mathematical truth. By the late 18th century, mathematicians’

intuitions were increasingly leading them astray. Putting calculus

on a firm logical foundation became a matter of some urgency,

and many of the best mathematicians of the 19th century applied

themselves to this task. The arithmetization of analysis was one of

the main motivations for early topological research.

An Alternative to Euclid’s Axioms

In the centuries after Euclid, many mathematicians tried to show

that Euclid had made a fundamental error: They believed that the

fifth postulate was not a postulate at all. They believed that the fifth

postulate could be proved as a logical consequence of the other

postulates and axioms. In other words, they thought that Euclid’s

collection of postulates and axioms was not logically independent

and that the fifth postulate, in particular, could be proved as a

Mathematics allows one to create

infinitely many distinct shapes—most

too complex to represent pictorially.

By the latter half of the 19th

century, it had become clear to many

mathematicians that geometrically

plausible arguments had no place

within analysis.