Tan S.T. Finite Mathematics for the Managerial, Life, and Social Sciences
Подождите немного. Документ загружается.


552 A INVERSE FUNCTIONS
EXAMPLE 3
Using the laws of logic, show that
p (p q) ⇔ ( p q)
Solution
p (p q) ⇔ ( p p) ( p q) By law 8
⇔ t ( p q) By law 11
⇔ p q By law 14
EXAMPLE 4
Using the laws of logic, show that
( p q) (p q) ⇔ p
Solution
( p q) (p q)
⇔ (p q) (p q)
By law 9
⇔ p (q q) By law 7
⇔ p t By law 11
⇔ p By law 14
A.4 Exercises
1. Prove the idempotent law for conjunction,
p p ⇔ p.
2. Prove the idempotent law for disjunction,
p p ⇔ p.
3. Prove the associative law for conjunction,
(p q) r ⇔ p (q r).
4. Prove the associative law for disjunction,
(p q) r ⇔ p (q r).
5. Prove the commutative law for conjunction,
p q ⇔ q p.
6. Prove the commutative law for disjunction,
p q ⇔ q p.
7. Prove the distributive law for disjunction,
p (q r) ⇔ (p q) (p r).
8. Prove De Morgan’s laws
a. (p q) ⇔
p q b. ( p q) ⇔ p q
In Exercises 9–18, determine whether the statement is a
tautology, a contradiction, or neither.
9. (p 씮 q) 씯씮 (p q) 10. (p q) (p 씯씮 q)
11. p 씮 (p q) 12. (p 씮 q) (q 씮 p)
13. (p 씮 q) 씯씮 (q 씮 p)
14. p (p 씮 q) 씮 q
15. (p 씮 q) (q) 씮 (p)
16. [(p 씮 q) (q 씮 r)] 씮
(p 씮 r)
17. [( p 씮 q) (q 씮 r)] 씮 (p 씮 r)
18. [p (q r)] 씯씮 [(p q) (p r)]
19. Let p and q denote the statements
p: The candidate opposes changes in the Social Security
system.
q: The candidate supports immigration reform.
Use De Morgan’s laws to state the negation of p q and
the negation of p q.
20. Let p and q denote the statements
p: The recycling bill was passed by the voters.
q: The tax on oil and hazardous materials was not
approved by the voters.
Use De Morgan’s laws to state the negation of p q and
the negation of p q.
In Exercises 21–26, use the laws of logic to prove the
propositions.
21. [p (q q) (p q)] ⇔ p (p q)
22. p (p q) ⇔ p q
23. (p q) (p r) ⇔ p (q r)
24. (p q) q ⇔ t
25. p (q r) ⇔ (p q) (p r)
26. p (q r) ⇔ r (q
p)
87533_10_APP_p537-578 1/30/08 10:27 AM Page 552
In this section, we discuss arguments and the methods used to determine the validity
of arguments.
The next example illustrates the form in which an argument is presented. Notice
that the premises are written separately above the horizontal line and the conclusion
is written below the line.
EXAMPLE 1
An argument is presented in the following way:
Premises: If Pam studies diligently, she passes her exams.
Pam studies diligently.
Conclusion: Pam passes her exams.
To determine the validity of an argument, we first write the argument in symbolic
form and then construct the associated truth table containing the prime propositions,
the premises, and the conclusion. We then check the rows in which the premises are
all true. If the conclusion in each of these rows is also true, then the argument is valid.
Otherwise, it is a fallacy.
EXAMPLE 2
Determine the validity of the argument in Example 1.
Solution
The symbolic form of the argument is
p 씮 q
p
q
Observe that the conclusion is preceded by the symbol , which is used to repre-
sent the word therefore. The truth table associated with this argument is shown in
Table 14. Observe that only row 1 contains true values for both premises. Since the
conclusion is also true in this row, we conclude that the argument is valid.
Argument
An argument or proof consists of a set of propositions p
1
, p
2
, . . . , p
n
, called the
premises, and a proposition q, called the conclusion. An argument is valid if and
only if the conclusion is true whenever the premises are all true. An argument
that is not valid is called a fallacy, or an invalid argument.
A.5 ARGUMENTS 553
TABLE 14
Propositions Premises Conclusion
pqp씮 qp q
TT TT T
TF FT F
FT TF T
FF TF F
A.5 Arguments
87533_10_APP_p537-578 1/30/08 10:27 AM Page 553

EXAMPLE 3
Determine the validity of the argument
If Michael is overtired, then he is grumpy.
Michael is grumpy.
Therefore, Michael is overtired.
Solution
The argument is written symbolically as follows:
p 씮 q
q
p
The associated truth table is shown in Table 15. Observe that the entries for the
premises in the third row are both true, but the corresponding entry for the conclu-
sion is false. We conclude that the argument is a fallacy.
When we consider the validity of an argument, we are concerned only with the
form of the argument and not the truth or falsity of the premises. In other words, the
conclusion of an argument may follow validly from the premises, but the premises
themselves may be false. The next example demonstrates this point.
EXAMPLE 4
Determine the validity of the argument
If I drive a car, then I eat lunch.
If I eat lunch, then I play Wii.
Therefore, if I drive a car, then I play Wii.
Solution
The symbolic form of the argument is
p 씮 q
q 씮 r
p 씮 r
The associated truth table is shown in Table 16. Since the conclusion is true in each
of the rows that contain true values for both premises, we conclude that the argu-
ment is valid. Note that the validity of the argument is not affected by the truth or
falsity of the premise “If I drive a car, then I eat lunch.”
A question that may already have arisen in your mind is: How does one determine
the validity of an argument if the associated truth table does not contain true values
for all the premises? The next example provides the answer to this question.
554 A INTRODUCTION TO LOGIC
TABLE 15
pqp씮 qqp
TTTTT
TFFFT
FTTTF
FF T FF
TABLE 16
pqrp씮 qq씮 rp씮 r
TTT T T T(✓)
TTF T F F
TFT F T T
TFF F T F
FTT T T T(✓)
FTF T F T
FFT T T T(✓)
FFF T T T(✓)
87533_10_APP_p537-578 1/30/08 10:27 AM Page 554

EXAMPLE 5
Determine the validity of the argument
The door is locked.
The door is unlocked.
Therefore, the door is locked.
Solution
The symbolic form of the argument is
p
p
p
The associated truth table is shown in Table 17. Observe that no rows contain true
values for both premises. Nevertheless, the argument is considered to be valid since
the condition that the conclusion is true whenever the premises are all true is not
violated. Again, we remind you that the validity of an argument is not determined by
the truth or falsity of its premises, but rather it is determined only by the form of the
argument.
The next proposition provides us with an alternative method for determining the
validity of an argument.
To prove this proposition, we must show that (a) if an argument is valid, then the given
proposition is a tautology, and (b) if the given proposition is a tautology, then the
argument is valid.
Proof of (a) Since the argument is valid, it follows that q is true whenever all
of the premises p
1
, p
2
, . . . , p
n
are true. But the conjunction ( p
1
p
2
. . .
p
n
)
is true when all the premises are true (by the definition of conjunction). Hence,
q is true whenever the conjunction is true, and we conclude that the conditional
( p
1
p
2
. . .
p
n
) 씮 q is true. (Recall that a conditional statement is always
true when its hypothesis is false. Hence, to show that a conditional is a tautology, we
need only prove that its conclusion is always true when its hypothesis is true.)
Proof of (b) Since the given proposition is a tautology, it is always true. Therefore,
q is true when the conjunction
p
1
p
2
. . .
p
n
is true. But the conjunction is true when all of the premises p
1
, p
2
, . . . , p
n
are true.
Hence, q is true whenever the premises are all true, and the argument is valid.
Having proved this proposition, we can now use it to determine the validity
of an argument. If we are given an argument, we construct a truth table for
( p
1
p
2
. . .
p
n
) 씮 q. If the truth table contains all Ts in its last column, then the
argument is valid; otherwise it is invalid. This method of proof is illustrated in the next
example.
Proposition
Suppose an argument consists of the premises p
1
, p
2
, . . . , p
n
and conclusion q.
Then, the argument is valid if and only if the proposition ( p
1
p
2
. . .
p
n
) 씮 q is a tautology.
A.5 ARGUMENTS 555
TABLE 17
p pp
TFT
FTF
87533_10_APP_p537-578 1/30/08 10:27 AM Page 555
EXAMPLE 6
Determine the validity of the argument
You return the book on time, or you will have to pay a fine.
You do not return the book on time.
Therefore, you will have to pay a fine.
Solution
The symbolic form of the argument is
p q
p
q
Following the method described, we construct the truth table for
[( p q) p] 씮 q
as shown in Table 18. Since the entries in the last column are all Ts, the proposition
is a tautology, and we conclude that the argument is valid.
By familiarizing ourselves with a few of the most commonly used argument
forms, we can simplify the problem of determining the validity of an argument. Some
of the argument forms most commonly used are the following:
1. Modus ponens (a manner of affirming), or rule of detachment
p 씮 q
p
q
2. Modus tollens (a manner of denying)
p 씮 q
q
p
3. Law of syllogisms
p 씮 q
q 씮 r
p 씮 r
The truth tables verifying modus ponens and the law of syllogisms have already
been constructed (see Tables 14 and 16, respectively). The verification of modus tol-
lens is left to you as an exercise. The next two examples illlustrate the use of these
argument forms.
EXAMPLE 7
Determine the validity of the argument
If the battery is dead, the car will not start.
The car starts.
Therefore, the battery is not dead.
556 A INTRODUCTION TO LOGIC
TABLE 18
pqp q p ( p q) p [( p q) p] 씮 q
TT T F F T
TF T F F T
FT T T T T
FF F T F T
87533_10_APP_p537-578 1/30/08 10:27 AM Page 556

Solution
As before, we express the argument in symbolic form. Thus,
p 씮 q
q
p
Identifying the form of this argument as modus tollens, we conclude that the given
argument is valid.
EXAMPLE 8
Determine the validity of the argument
If mortgage rates are lowered, housing sales increase.
If housing sales increase, then the prices of houses increase.
Therefore, if mortgage rates are lowered, the prices of houses increase.
Solution
The symbolic form of the argument is
p 씮 q
q 씮 r
p 씮 r
Using the law of syllogisms, we conclude that the argument is valid.
A.5 ARGUMENTS 557
A.5 Exercises
In Exercises 1–16, determine whether the argument is
valid.
1. p 씮 q 2. p q
q 씮 r p
p 씮 r q
3. p q 4. p 씮 q
p q
q p
5. p 씮 q 6. p 씮 q
pq r
q p r
7. p 씯씮 q 8. p q
q p 씮 q
p p q
9. p 씮 q 10. p 씮 q
q 씮 pp q
p 씯씮 q q
11.
p 씯씮 q 12. p 씮 q
q 씯씮 rq씯씮 r
p 씯씮 r p
r
13. p r 14. p 씯씮 q
q rq r
p 씮 r
r
p 씮 r
15. p 씯씮 q 16. p 씮 q
q rr씮 q
pp q
p 씮 r p r
In Exercises 17–22, represent the argument symbolically
and determine whether it is a valid argument.
17. If Carla studies, then she passes her exams.
Carla did not study.
Therefore, Carla did not pass her exams.
18. If Tony is wealthy, he is either intelligent or a good business-
man.
Tony is intelligent and he is not a good businessman.
Therefore, Tony is not wealthy.
19. Steve will attend the matinee and/or the evening show.
If Steve doesn’t go to the matinee show,
then he will not go to the evening show.
Therefore, Steve will attend the matinee show.
20. If Mary wins the race, then Stacy loses the race.
Neither Mary nor Linda won the race.
Therefore, Stacy won the race.
21. If mortgage rates go up, then housing prices will go up.
If housing prices go up, more people will rent houses.
More people are renting houses.
Therefore, mortgage rates went up.
87533_10_APP_p537-578 1/30/08 10:27 AM Page 557
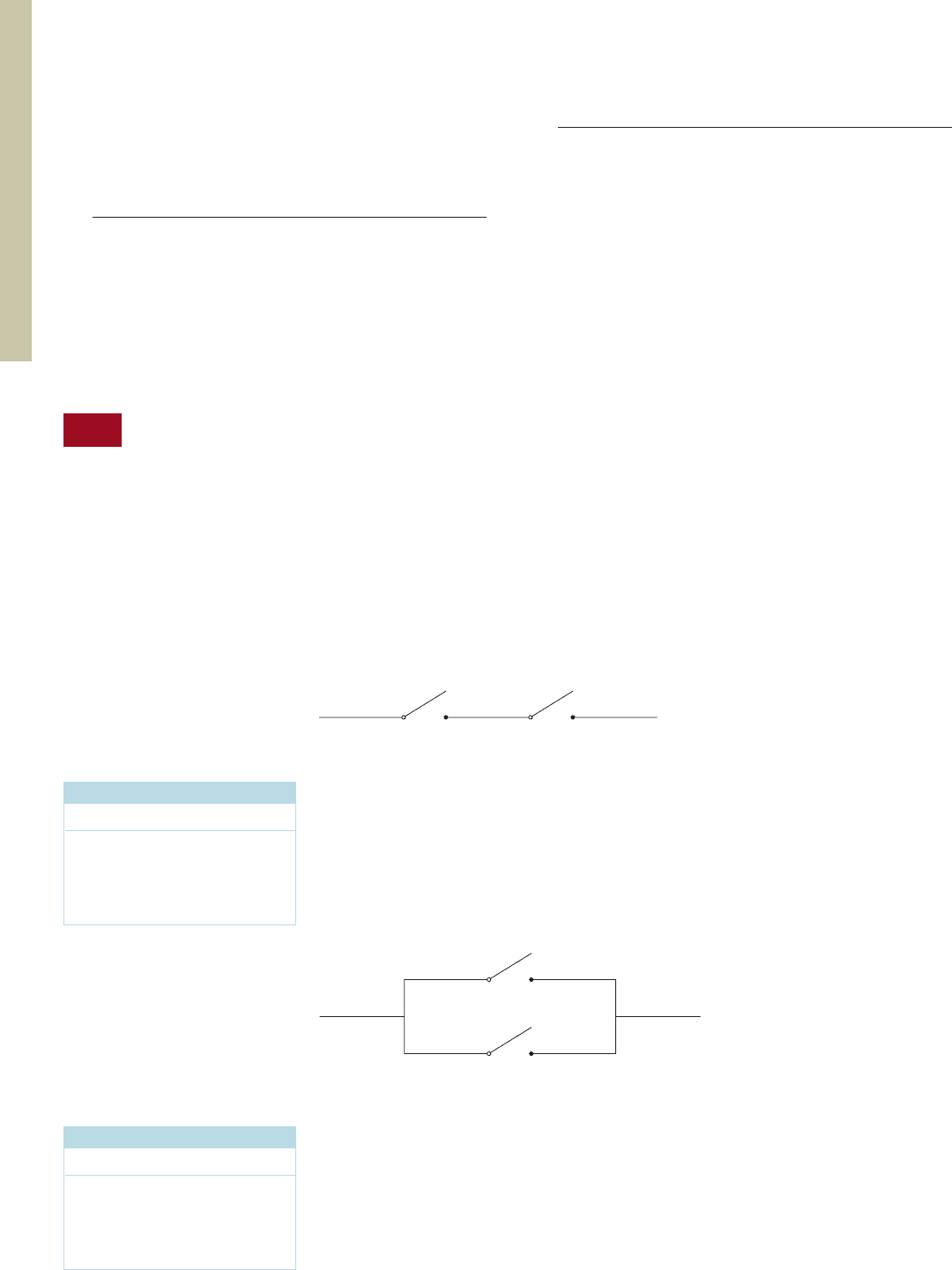
558 A INVERSE FUNCTIONS
22. If taxes are cut, then retail sales increase.
If retail sales increase, then the unemployment rate will
decrease.
If the unemployment rate decreases, then the incumbent
will win the election.
Therefore, if taxes are not cut, the incumbent will not win
the election.
23. Show that the following argument is valid.
If George prepares gourmet food, then he is a good cook.
If Brenda does not prepare gourmet food, then Sarah buys
fast food.
Sarah does not buy fast food.
Therefore, George does not prepare gourmet food, and
Brenda does not prepare gourmet food.
24. What conclusion can be drawn from the following state-
ments?
His date is pretty, or she is tall and skinny.
If his date is tall, then she is a brunette.
His date is not a brunette.
25. Show that modus tollens is a valid form of argument.
A.6 Applications of Logic to Switching Networks
In this section, we see how the principles of logic can be used in the design and analysis
of switching networks. A switching network is an arrangement of wires and switches
connecting two terminals. These networks are used extensively in digital computers.
A switch may be open or closed. If a switch is closed, current will flow through
the wire. If it is open, no current will flow through the wire. Because a switch has
exactly two states, it can be represented by a proposition p that is true if the switch is
closed and false if the switch is open.
Now let’s consider a circuit with two switches p and q. If the circuit is constructed
as shown in Figure 1, the switches p and q are said to be in series.
For such a network, current will flow from A to B if both p and q are closed, but
no current will flow if one or more of the switches is open. Thinking of p and q as
propositions, we have the truth table shown in Table 19. (Recall that T corresponds to
the situation in which the switch is closed.) From the truth table we see that two
switches p and q connected in series are analogous to the conjunction p q of the
two propositions p and q.
If a circuit is constructed as shown in Figure 2, the switches p and q are said to be
connected in parallel.
For such a network, current will flow from A to B if and only if one or more of
the switches p or q is closed. Once again, thinking of p and q as propositions, we have
the truth table shown in Table 20. From the truth table, we conclude that two switches
p and q connected in parallel are analogous to the inclusive disjunction p q of the
two propositions p and q.
EXAMPLE 1
Find a logic statement that represents the network shown in Figure 3.
By constructing the truth table for this logic statement, determine the conditions
under which current will flow from A to B in the network.
p
A
B
q
q
p
A
B
FIGURE 1
Two switches connected in series
FIGURE 2
Two switches connected in parallel
TABLE 19
pq
TTT
TFF
FTF
FFF
TABLE 20
pq
TTT
TFT
FTT
FFF
87533_10_APP_p537-578 1/30/08 10:27 AM Page 558

Solution
The required logic statement is p (q r). Next, we construct the truth
table for the logic statement p (q r) (Table 21).
From the truth table, we conclude that current will flow from A to B if and only if
one of the following conditions is satisfied:
1. p, q, and r are all closed.
2. p and q are closed, but r is open.
3. p and r are closed, but q is open.
In other words, current will flow from A to B if and only if p is closed and either q
or r or both q and r are closed.
Before looking at some additional examples, let’s remark that p represents a
switch that is open when p is closed and vice versa. Furthermore, a circuit that is
always closed is represented by a tautology, p p, whereas a circuit that is always
open is represented by a contradiction, p p. (Why?)
EXAMPLE 2
Given the logic statement ( p q) (r s t), draw the corre-
sponding network.
Solution
Recalling that the disjunction p q of the propositions p and q repre-
sents two switches p and q connected in parallel and the conjunction p q repre-
sents two switches connected in series, we obtain the following network (Figure 4).
When used in conjunction with the laws of logic, the theory of networks devel-
oped so far is a useful tool in network analysis. In particular, network analysis enables
us to find equivalent, and often simpler, networks, as the following example shows.
p
B
q
A
r
~t
s
q
B
r
p
A
A.6 APPLICATIONS OF LOGIC TO SWITCHING NETWORKS 559
FIGURE 3
We want to determine when the current
will flow from A to B.
FIGURE 4
The network that corresponds to the logic
statement
( p q) (r s t)
TABLE 21
pqrq rp (q r)
TTT T T
TTF T T
TFT T T
TFF F F
FTT T F
FTF T F
FFT T F
FFF F F
87533_10_APP_p537-578 1/30/08 10:27 AM Page 559
560 A INVERSE FUNCTIONS
EXAMPLE 3
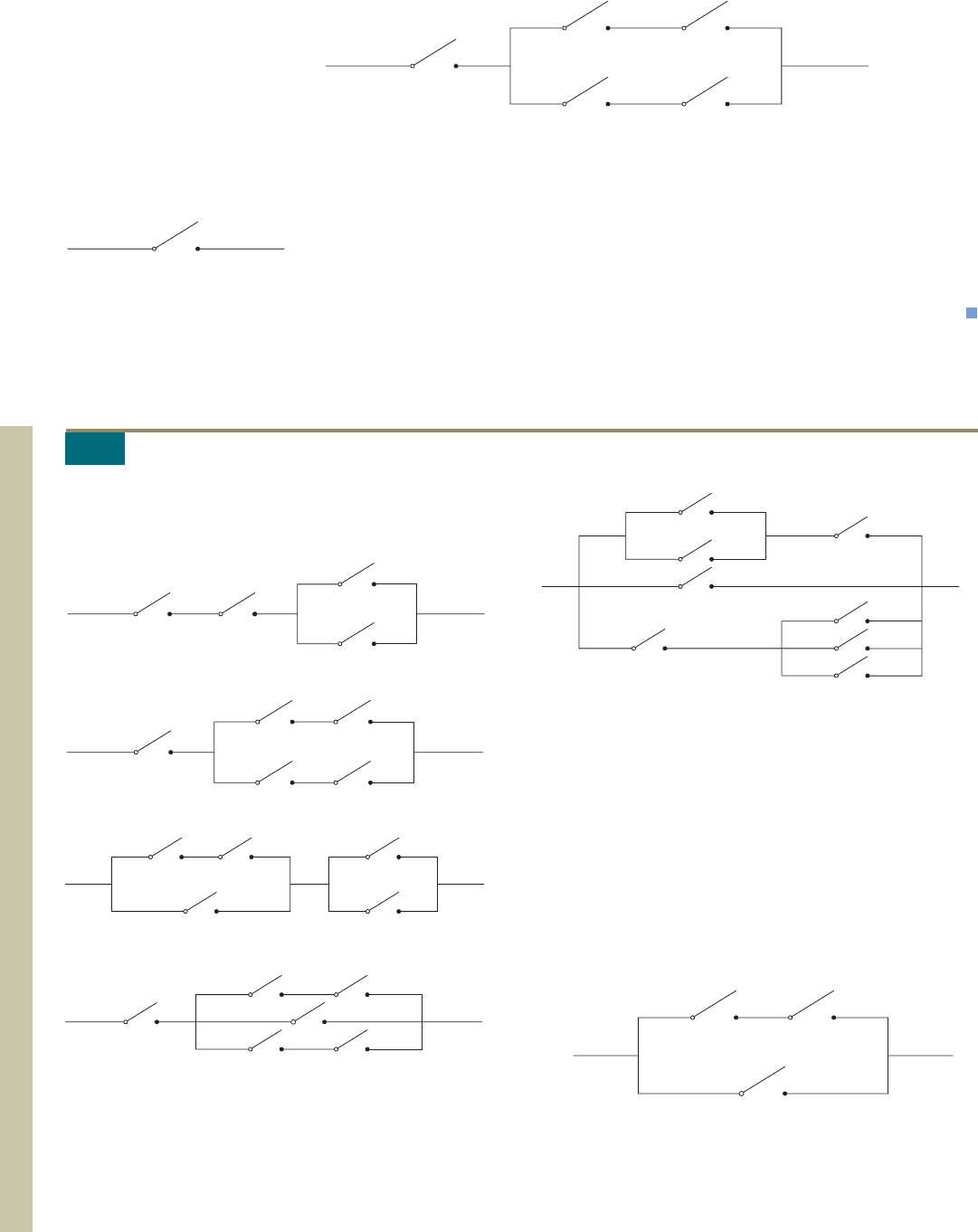
Find a logic statement representing the network shown in Figure 5.
Also, find a simpler but equivalent network.
Solution
The logic statement corresponding to the given network is p
[(p q) (p q)]. Next, using the rules of logic to simplify this statement, we
obtain
p [(p q) (p q)] B p [p (q q)]
Distributive law
B p p Tautology
B p
Thus, the network shown in Figure 6 is equivalent to the one shown in Figure 5.
p
B
p
p
A
q
~
q
FIGURE 5
We want to find the logic statement that
corresponds to the network shown in the
figure.
p
A
B
FIGURE 6
The network is equivalent to the one
shown in Figure 5.
A.6 Exercises
In Exercises 1–5, find a logic statement corresponding to
the network. Determine the conditions under which cur-
rent will flow from A to B.
1.
2.
3.
4.
q
B
~r
p
A
~q
r
~p
p
B
r
A
q ~r
p
q
B
s
p
r
t
A
r
B
s
qp
A
5.
In Exercises 6–11, draw the network corresponding to
the logic statement.
6. p (q r) 7. ( p q) r
8. [ p (q r)] q
9. ( p q) [r (r p)]
10. (p q) ( p q)
11. ( p q) [(r q) (s p)]
In Exercises 12–15, find a logic statement corresponding
to the network. Then find a simpler but equivalent logic
statement.
12.
q
B
~q
A
p
B
~q
A
r
r
~p
p
q
p
~r
87533_10_APP_p537-578 1/30/08 10:27 AM Page 560

15.
16. A hallway light is to be operated by two switches, one lo-
cated at the bottom of the staircase and the other located at
the top of the staircase. Design a suitable network.
Hint: Let p and q be the switches. Construct a truth table for the
associated propositions.
B
q
p
A
~p
r
q
A.6 APPLICATIONS OF LOGIC TO SWITCHING NETWORKS 561
13.
14.
~q
B
r
~p
A
p
q
~q
B
~p
p
A
q
87533_10_APP_p537-578 1/30/08 10:27 AM Page 561
