Таненбаум Э. Распределенные системы. Принципы и парадигмы

Подождите немного. Документ загружается.

8.7. Пример — электронные платежные системы

531

Информация

Сторона

Продавец

Покупа-

тель

Банк

Наблю-

датель

Продавец

Полностью

Покупа-

тель

Полностью

Частично

Дата

Полностью

Сумма

Полностью

Товар

Полностью

Нет

Полностью

Рис. 8.43. Сокрытие информации в традиционных системах,

использующих кредитные карты

Понятно, что оплата кредитной картой не обеспечивает особой закрытости,

оставляя нам лишь анонимность. Электронные версии платежных систем долж-

ны предоставлять как минимум такой же, а по возможности и больший уровень

защиты. Например, обычно недопустимо, чтобы номер кредитной карты пересы-

лался по открытым сетям в виде простого текста.

8.7.3. Примеры протоколов

Чтобы лучше разобраться в вопросах заш.иты электронных платежных систем,

давайте кратко обсудим две характерные системы. Сначала мы поговорим о сис-

теме, позволяющей проводить платежи цифровыми деньгами. Затем рассмотрим

стандартизованный протокол для безопасных транзакций с кредитными картами

через Интернет.

E-cash

Существует несколько электронных платежных систем, которые базируются на

концепции цифровых денег. Одной из наиболее известных является система e-cash,

описание которой можно найти в [94, 95]. Основной целью при разработке этой

системы было введение анонимности в платежи. Чтобы понять, как работает сис-

тема e-cash, рассмотрим сначала не анонимную систему на основе наличных де-

нег.

Допустим, Алиса хочет купить некоторые товары у Боба через сеть на общую

сумму 12 долларов, используя цифровые деньги. Сначала она связывается со

своим банком и просит снять 12 долларов с ее счета. Банк создает цифровые

деньги в форме подписанных виртуальных банкнот на определенную сумму,

причем каждая банкнота имеет уникальную ассоциированную с ней подпись.

Так, например, виртуальная банкнота в 10 долларов может быть подписана спе-

циальным, принадлежащим банку закрытым ключом iCjo, а однодолларовая банк-

нота

—

другим специальным закрытым ключом

К~\.

Для предотвращения копи-

рования виртуальных банкнот каждая из них имеет уникальный серийный но-

мер,

с помощью которого банк может проверить факт повторного использования

банкноты.

532 Глава 8. Защита

В нашем примере Алиса получает в своем банке десятидолларовую банкноту

и две однодолларовых, которые позднее передает Бобу. По подписи банка Боб

может проверить, что банкноты хотя и виртуальные, но не поддельные. Однако

для проверки на попытку повторного использования банкнот ему необходимо

связаться с банком, который по серийным номерам проверит, не применялись ли

эти банкноты для оплаты раньше. Если это не попытка повторного использова-

ния виртуальных банкнот. Боб отправляет сообщение ОК как знак того, что го-

тов принять эти деньги. Отметим, что Бобу все равно нужно связаться с банком,

поскольку банк должен также проверить целостность банкнот.

Основной минус этой схемы состоит в том, что банк вынужден отслеживать

серийные номера всех цифровых банкнот, то есть точно контролировать все де-

нежные потоки. Если Алиса запросит десятидолларовую банкноту, банк должен

записать серийный номер банкноты, выданной Алисе, и позже отследить, как Боб

использует ее для оплаты. Не существует другого способа понять, что Алиса пла-

тит Бобу, если не будет некоей третьей стороны, которая примет платеж от Али-

сы,

поверив ей на слово, что эти деньги еще ни разу не использовались.

Эту систему необходимо дополнить, чтобы не нужно было отслеживать, ка-

кие цифровые банкноты кому были переданы, сохраняя при этом защищенность

банкнот от попыток подделки или повторного использования. Как показано

в [93], такая защита может быть осуществлена при помощи так называемой сле-

пой подписи

{blind

signature).

Принцип, лежащий в основе слепой подписи, про-

ще всего объяснить на примере конверта, покрытого изнутри копировальной бу-

магой. [94]. Если положить внутрь конверта обычную бумагу, все, написанное на

конверте, отпечатается и на бумаге внутри него.

Для Алисы, получающей свою десятидолларовую банкноту, подписанную ее

банком, это выглядит так, будто она помещает банкноту в конверт с копироваль-

ной бумагой и просит свой банк поставить подпись на конверте. Банк снимает 10

долларов со счета Алисы и ставит свою подпись на конверте. После этого банк

никогда не увидит саму банкноту, но в любой момент может прочитать свою де-

сятидолларовую подпись, стоящую на конверте. После этого Алиса может исполь-

зовать банкноту как обычные деньги. Эта схема отлично работает, если учесть,

что банк ежедневно подписывает множество десятидолларовых виртуальных

банкнот. В этом случае, когда Боб передаст в банк десятидолларовую банкноту

и потребует перечислить 10 долларов на свой счет, отследить Алису по этой банк-

ноте будет невозможно.

Чтобы понять, как работают эти подписи в алгоритмах RSA, используем ту же

нотацию, что и ранее при описании принципов RS

А:

п= р х

д^

где

pnq

—

два боль-

ших простых (и секретных) числа. Число d вычисляется на основе этих простых

чисел как d ^ {р - \) х {q - I),

г.

е получается следующим образом: в х

6? = 1

modz.

Предположим, Алиса хочет получить со своего банковского счета десятидол-

ларовую банкноту. Фактически она сама создает себе эту банкноту, но нуждает-

ся в банковской подписи для ее подтверждения, причем так, чтобы банк впо-

следствии был не в состоянии проследить ее движение. Она создает случайное

число k между i и пи делает т нечитаемым, скрывая его в сообщении

t =

mk^

mod п.

8.7. Пример — электронные платежные системы 533

Банк подписывает сообщение t своим защищенным ключом iCJo (в нашем

примере

—

б/), превращая его в сообщение t^. Отметим, что мы используем клю-

чи,

специально предназначенные для десятидолларовых банкнот. Для изготовле-

ния банкнот другого достоинства требуются другие ключи. Когда Алиса получит

сообщение t^, она раскроет его, делая следующие вычисления:

S = t^/k mod п = (mk^Y/k mod п =

m^k^^~

mod п =

т^

mod п.

С этого момента она имеет в своем распоряжении десятидолларовую банкно-

ту, которая подписана банком так, что банк никогда ее не видел. Теперь Алиса

может использовать т^ в качестве десятидолларовой банкноты для того, чтобы

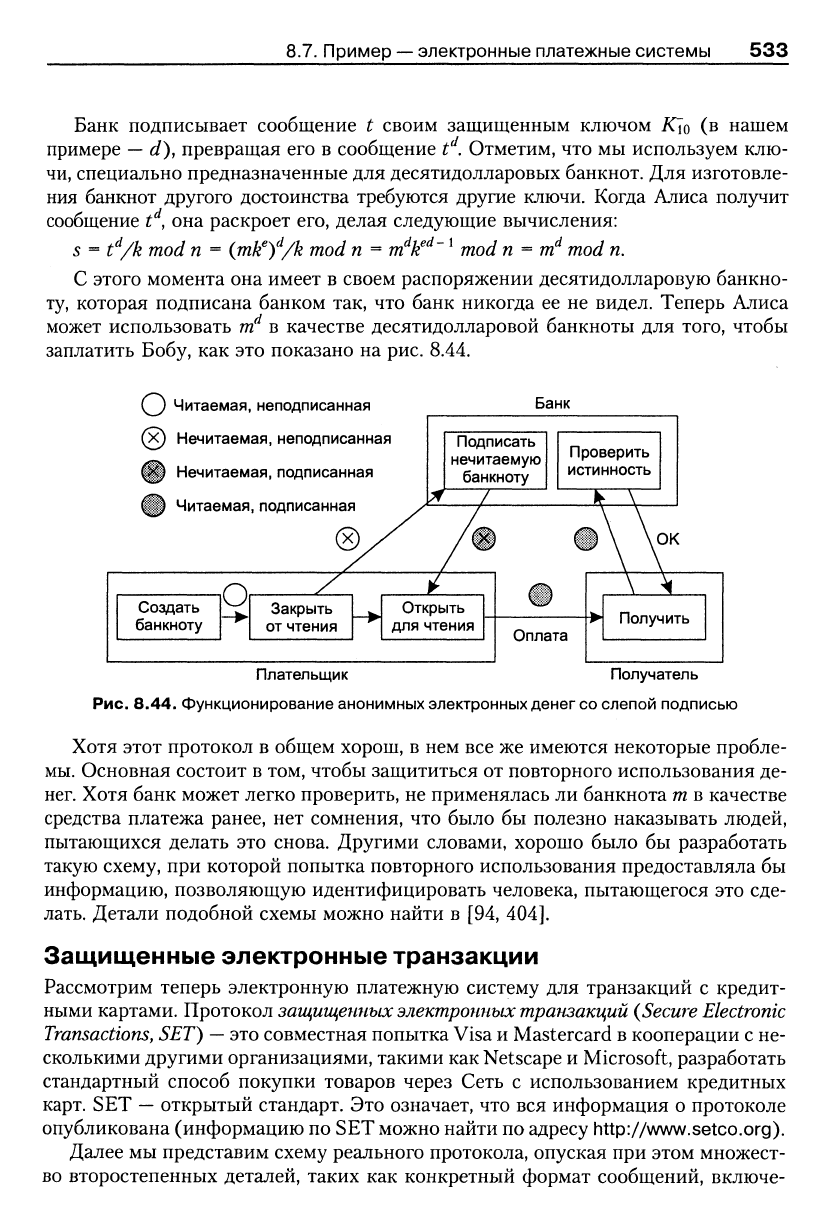
заплатить Бобу, как это показано на рис. 8.44.

Q Читаемая, неподписанная

(х) Нечитаемая, неподписанная

@ Нечитаемая, подписанная

(3 Читаемая, подписанная

Банк

Подписать

нечитаемую

банкноту

Создать

банкноту

Проверить

истинность

Закрыть

от чтения

Открыть

для чтения

ок

Оплата

Получить

Плательщик Получатель

Рис. 8.44. Функционирование анонимных электронных денег со слепой подписью

Хотя этот протокол в общем хорош, в нем все же имеются некоторые пробле-

мы.

Основная состоит в том, чтобы защититься от повторного использования де-

нег. Хотя банк может легко проверить, не применялась ли банкнота т в качестве

средства платежа ранее, нет сомнения, что было бы полезно наказывать людей,

пытающихся делать это снова. Другими словами, хорошо было бы разработать

такую схему, при которой попытка повторного использования предоставляла бы

информацию, позволяющую идентифицировать человека, пытающегося это сде-

лать.

Детали подобной схемы можно найти в [94, 404].

Защищенные электронные транзакции

Рассмотрим теперь электронную платежную систему для транзакций с кредит-

ными картами. Протокол

защищегтых электронных транзакций {Secure Electronic

Transactions

SET)

—

это совместная попытка Visa и Mastercard в кооперации с не-

сколькими другими организациями, такими как Netscape и Microsoft, разработать

стандартный способ покупки товаров через Сеть с использованием кредитных

карт. SET

—

открытый стандарт. Это означает, что вся информация о протоколе

опубликована (информацию по SET можно найти по адресу http://www.setco.org).

Далее мы представим схему реального протокола, опуская при этом множест-

во второстепенных деталей, таких как конкретный формат сообщений, включе-

534 Глава 8. Защита

ние изменений, отметки времени и пр. Основная задача этого описания состоит

в том, чтобы дать представление о SET как многостороннем протоколе для элек-

тронных платежей при помощи кредитных карт.

В SET использована важная новая концепция двойной подписи. Прежде чем

мы перейдем к обсуждению различных этапов протокола, нам следует в ней ра-

зобраться. Рассмотрим следующую проблему: Алиса хочет купить у Боба не-

которые товары, пользуясь кредитной картой. Все, что она должна сделать при

этом,

—

отправить Бобу информацию о заказанных товарах вместе с данными о

своей кредитной карте. Боб должен быть в состоянии передать эти данные

в банк для завершения процесса оплаты за товары. Нам необходимо связать за-

каз и платежную информацию.

Один из способов — поместить всю необходимую информацию в одно сооб-

щение и потребовать от Алисы, чтобы она подписала его. Однако в этом случае и

Боб,

и банк для проверки подписи Алисы будут вынуждены получать как заказ,

так и платежную информацию. Соответственно, банк узнает, что заказывала

Алиса. Обычно эти данные должны быть известны только Алисе и Бобу. Точно

так же Алиса не хочет, чтобы Бобу стали известны детали информации о произ-

веденной оплате. Данные о кредитоспособности Алисы

—

дело банка, а не Боба.

Решение будет следующим. Пусть т\ и

т2

обозначают соответственно заказ и

платежную информацию. Двойная подпись (dual signature) состоит в построении

дайджеста сообщения md[

Н{т\) для т^ и

md2 =

Н(т2) для т2 с последующим

построением третьего дайджеста путем слияния mdi и

md2:

mdduai

= H{concat(jndu

mdi)).

Этот дайджест

mdduai

затем подписывается Алисой с использованием ее

закрытого ключа. Теперь Алиса посылает Бобу сообщение [т\, mdjuah ^d2,

K~\{mdduai)]^

которое позволяет ему идентифицировать Алису и убедиться, что

именно она поставила подпись под всем сообщением. Однако Боб не в состоя-

нии прочесть

1712.

Для обозначения двойной подписи сообщений т\ и ^2, из кото-

рых открыто только

/771,

МЫ ИСПОЛЬЗуСМ запись [7771|7772]л*

[7771|/772]л = \ши Щшг), Н{сопса1{ти 7772)), K~A{H{concat{rn\, 7772)))].

Давайте обсудим теперь основы протокола SET. Этапы протокола иллюстри-

рует рис. 8.45.

Мы предпо.71агаем, что Алиса хочет заплатить Бобу. Первое, что ей необходи-

мо сделать, — послать Бобу заказ и платежную информацию. На рисунке это

действие показано в виде сообщения 1. Информация о заказе обозначена как order,

информация о платеже

—

как pay_info. Алиса создает дважды подписанное сооб-

щение [order

pay_info]A. Платежная информация, которая должна быть прочи-

тана только в банке, шифруется сеансовым ключом КлмпЬ который банк создал

для Алисы. Этот ключ также посылается Бобу, но зашифрованный открытым

ключом банка

Klank-

После того как Боб проверит сообщение Алисы, он пересылает платежную

информацию в банк и запрашивает авторизацию оплаты. При этом он создает се-

ансовый ключ

Кв\,ьапку

который используст ДЛЯ шифроваиия своего запроса auth.

Этот запрос пересылается в банк вместе с информацией Алисы об оплате, а ключ

Кв\мапк

шифруется открытым ключом банка. Все это показано на рисунке как со-

общение 2.

8.8. Итоги

535

[order I payJnfolA,

.bank

(payjnfo), KJank

(KA

.bank/

[рау_ОК]в

^^Bl.bank (auth), Kbank (^BLbank)'

KA .bank

(payjnfo),

К^зпк

(KA.bank)

Кв2.Ьапк ([auth_OK]bank). ^в (Квг.Ьапк).

Квз .bank

([caplbank), K^ (Квз

.bank/

Кв4.Ьапк ([Рау_те]в), Кьапк (Кв4.Ьапк).

•^ВЗ.Ьапк ([Cap]bank).

K^ank

(^вз.Ьапк)

Квб.Ьапк ([сар_ОК]ьапк)'Кв (^BS.bank)

Рис. 8.45. Этапы протокола SET

Допустим, что банк признал действительность оплаты. В этом случае он воз-

вращает Бобу подписанное сообщение о прохождении авторизации auth_OK,

зашифрованное новообразованным сеансовым ключом КщмпЬ который, в свою

очередь, зашифрован открытым ключом Боба. Этот ответ, обозначенный как со-

обще}П1е 3, содержит также и так называемое сообщение о получении {capture

message),

которое потребуется позже, когда Боб действительно будет получать

деньги из банка. Сообщение о получении однозначно ассоциируется с конкрет-

ной транзак1и1ей посредством идентификатора транзакции. Этот идентификатор

также используется и в сообщениях order и payjnfo. Сообщение о получении

подписывается банком и шифруется при помощи третьего сеансового ключа.

Когда Боб получает от банка «добро», он посылает Алисе подписанное под-

тверждение, показанное на рисунке как сообщение 4.

Теперь Боб хочет получить свои деньги. Он посылает банку сооби1ение рау_те

вместе с ранее полученным сообщением о получении. И вновь для шифрования

сообщения рау_те создается и используется новый сеансовый ключ. Это сооб-

щение 5.

И, наконец, после того как банк проверит сообщение о получении, он возвра-

щает Бобу подтверждение сар_ОК, зашифрованное сеансовым ключом

Квзмапк-

Хотя на рис. 8.45 это и не указано, в протоколе SET на каждом из шагов вы-

полняется аутентргфикация путем посылки сертификатов всякий раз, когда воз-

никает необходимость в использовании открытого ключа. С этой целью в прото-

коле задействуется иерархия сертифицирующих организаций, сходная с ранее

обсуждавшейся иерархией моделей доверия в почте РЕМ. Детали этой модели,

равно как и протокола, можно найти в

[407].

8.8. Итоги

Защита играет в распределенных системах чрезвычайно важную роль. Распреде-

ленные системы должны предоставлять пользователям и разработчикам меха-

536 Глава 8. Защита

низмы, обеспечивающие реализацию разнообразных правил защиты. Разработка

и правильное применение подобных механизмов обычно делают обеспечение за-

щиты в распределенных системах сложной инженерной задачей.

Следует выделить три важных момента. Первый из них состоит в том, что

распределенные системы должны иметь средства для организации защищенных

каналов связи между процессами. Защищенный канал в принципе предоставля-

ет средства взаимной аутентификации сторон и защищает сообщения во время

пересылки от фальсификации. Защищенный канал обычно предоставляет также

и средства поддержания конфиденциальности. Это означает, что никто, кроме

связавшихся друг с другом сторон, не в состоянии читать передаваемые по кана-

лу сообщения.

Одним из серьезных вопросов, который следует решить при проектировании,

является выбор между исключительно симметричной криптосистемой (основан-

ной на совместном использовании секретных ключей) или сочетанием ее с сис-

темой с открытым ключом. В текущей практике криптография с открытым клю-

чом используется для рассылки общих секретных ключей. Последние известны

также как сеансовые ключи.

Второй вопрос защиты распределенных систем

—

это контроль доступа, или

авторизация. Авторизация касается защиты ресурсов, чтобы только процессы,

имеющие соответствующие права доступа, могли получать доступ к соответст-

вующим ресурсам и использовать их. После аутентификации процесса всегда про-

изводится контроль доступа.

Существует два способа реализации контроля доступа. Во-первых, каждый из

ресурсов может поддерживать собственный список доступа, в котором перечис-

ляются права доступа всех пользователей или процессов. Кроме того, процесс

может иметь сертификат, точно устанавливающий его права на определенный

набор ресурсов. Основное достоинство сертификатов состоит в том, что процесс

может с легкостью передать свой талон другому процессу, делегировав свои пра-

ва доступа. Однако сертификаты имеют и недостаток

—

их обычно не просто от-

зывать.

Особое внимание следует уделить вопросам управления доступом в случае

мобильного кода. Помимо необходимости защиты мобильного кода от вредонос-

ных хостов, обычно важнее защитить хосты от вредоносного мобильного кода.

Для этого существуют различные способы, из которых наиболее часто применя-

ется так называемое сито. Однако сито чрезмерно ограничивает возможности

программ, поэтому для решения проблемы были разработаны более гибкие мето-

ды на основе реально защищенных доменов.

Третий ключевой вопрос защиты распределенных систем

—

это управление

защитой. Здесь есть два важных аспекта

—

управление ключами и управление

авторизацией. Управление ключами включает распространение криптографиче-

ских ключей, в котором значительную роль играют сертификаты, выдаваемые

доверенным третьим лицом. В деле управления авторизацией важны сертифика-

ты атрибутов и делегирование.

Kerberos — это широко распространенная система защиты, основанная на

шифровании общих секретных ключей. Ее основное назначение

—

аутентифика-

8.8. Итоги 537

дня, хотя она также поддерживает протоколы управления доступом и делегиро-

вание прав доступа.

SESAME — это типичный пример системы защиты, которая встраивается

в распределенные системы. Она основана на комбинированном использовании

шифрования открытых ключей и общих секретных ключей. Она многое взяла от

системы Kerberos и совместима с Kerberos.

И, наконец, важной областью использования распределенных систем являют-

ся электронные платежные системы. Интерес они представляют с точки зрения

тех сторон, которые могут связываться через глобальные сети. Особое внимание

часто уделяется обеспечению определенного уровня анонимности покупателя,

который возможен в традиционных расчетных системах на базе наличных денег

и в их электронных двойниках.

Вопросы и задания

Какие механизмы могут предоставляться в распределенных системах в каче-

стве служб защиты разработчикам приложений, которые, как говорилось в гла-

ве 5, в проектировании систем доверяют только сквозным аргументам?

Можно ли в случае подхода RISSC сосредоточить все службы защиты на за-

щищенных серверах?

Предположим, что вас попросили разработать распределенное приложение,

которое должно помочь преподавателям принимать экзамены. Укажите как

минимум три условия, которые должны стать частью правил защиты такого

приложения.

Будет ли безопасно объединить сообщения 3 и 4 протокола аутентификации,

приведенного на рис. 8.11, в Х^,в(^5» ^л)?

Почему (см. рис. 8.14) для центра KDC очевидно, что он общался с Алисой,

при получении запроса на передачу секретного ключа, который Алисд может

использовать совместно с Бобом?

6. Почему вместо случайного числа

попсе

нельзя использовать отметку времени?

В сообщении 2 протокола аутентификации Нидхема—Шредера талон шифру-

ется секретным ключом, который совместно используют Алиса и KDC. Явля-

ется ли это шифрование необходимым?

8. Можем ли мы безопасно изменить протокол, приведенный на рис. 8.19, так,

чтобы сообщение 3 содержало только запрос i^^?

9. Придумайте простой алгоритм аутентификации с использованием подписей

для криптосистемы с открытым ключом.

10.

Пусть Алиса хочет передать Бобу сообщение. Вместо того чтобы шифровать

т открытым ключом Боба

K'^Q,

она создает сеансовый ключ

iC^

и посылает

[К/^^в{гп),

i^K^л,5)]• Почему эта схема обычно оказывается лучше? (Подсказ-

ка: примите во внимание вопросы производительности.)

И. Как может быть реализована смена ролей в матрице контроля доступа?

538 Глава 8. Защита

12.

Как реализованы списки контроля доступа в файловой системе UNIX?

13.

Как организация может заставить использовать для доступа в Web прокси-

шлюз и предотвратить прямой доступ своих пользователей к внешнрш web-

серверам?

14.

В какой степени (см. рис. 8.28) использование в качестве мандатов ссылок на

объекты Java действительно зависит от языка Java?

15.

Назовите три проблемы, с которыми сталкиваются разработчики интерфей-

сов,

когда для защиты от неавторизованного доступа к локальным ресурсам

со стороны мобильных программ они вынуждены, как описано в соответст-

вующем разделе, вставлять инструкции включения и отключения прр1виле-

гий.

16.

Назовите несколько достоинств и недостатков использования централизован-

ного сервера управления ключами.

17.

Протокол обмена ключами Диффи—Хеллмана можно использовать также и при

создания общего секретного ключа для трех сторон. Объясните, как.

18.

В протоколе обмена ключами Диффи—Хеллмана отсутствует аутентификация.

Из-за этого третья сторона, Чак, может легко вмешаться в обмен ключами ме-

жду Алисой и Бобом, после чего проникнуть через механизмы защиты. Объ-

ясгнгге, как.

19.

Приведите простой способ отзыва мандатов в системе Amoeba.

20.

Имеет ли смысл ограничение срока жизни сеансового ключа? Если да, приве-

дите пример.

21.

Какова роль отметки времени в сообщении 6 на рис.

8.37?

Почему она долж-

на быть зашифрована?

22.

Придайте законченный вид рис. 8.37, добавив связь для аутентификации Али-

сой и Бобом друг друга.

23.

Рассмотрим связь между Алисой и Бобом и службу аутентификацрш AS, та-

кую как в системе SESAME. Какая разница (если она есть) между сообще-

ниями

Ш1

= K^s(KA,As(data)) и ^2 = K^^AsiK^sidata))?

24.

Определите как минимум два различных уровня атомарности транзакций

в электронных платежных системах.

25.

Покупатель в системе e-cash до использования денег, полученных в банке, обыч-

но делает паузу случайной длительности. Почему?

26.

Анонимность продавца в платежных системах нередко запрещена. Почему?

27.

Рассмотрим электронную платежную систему, в которой покупатель посыла-

ет деньги продавцу (удаленному). Постройте таблицу (см. рис. 8.42 и 8.43),

описывающую сокрытие информации.

Глава 9

Распределенные

системы объектов

9.1.C0RBA

9.2. DCOM

9.3. Globe

9.4. Сравнение систем CORBA, DCOM и Globe

9.5. Итоги

В этой главе мы переходим от обсуждения принципов построения распределен-

ных систем к изучению различных парадигм, используемых при

PIX

построении.

Первая парадигма

—

это распределенные объекты. В распределенных системах

объектов понятие объекта играет ключевую роль для реализацрш прозрачности

распределения. В принципе считать объектами можно все; клиенты получают

службы и ресурсы в форме объектов, к которым они могут обращаться.

Распределенные объекты образуют важную парадигму, поскольку все аспек-

ты распределения относительно просто скрыть за интерфейсом объектов. Кроме

того,

объекты могут присутствовать фактически повсюду, и это также усиливает

значение этой парадигмы для построения систем. Распределенные объекты ле-

жат в основе двух важных, широко распространенных распределенных систем,

которые мы обсудим в этой главе.

В качестве первого примера мы рассмотрим CORBA, промышленный стан-

дарт распределенных систем. В настоящее время используется множество сис-

тем CORBA, и их разработка и стандартизация развиваются по мере того, как

растет число установленных систем.

Нашим вторым примером будет DCOM корпорации Microsoft. DCOM мож-

но рассматривать как систему промежуточного уровня, реализованную поверх

различных операционных систем Windows, начиная с Windows 95. Фактически

все приложения Windows опираются на предоставляемую DCOM функциональ-

ность. Таким образом, DCOM можно считать наиболее широко распространен-

ной распределенной системой промежуточного уровня.

540 Глава 9. Распределенные системы объектов

Кроме этих двух коммерческих систем известно также множество исследо-

вательских работ по построению различных распределенных систем объектов.

В этой главе мы рассмотрим экспериментальную систему Globe, которая разра-

батывается в настоящее время в рамках исследовательского проекта по глобаль-

ным распределенным сетям. Интересной особенностью Globe, которая отличает

ее от систем типа CORBA и DCOM, является тот факт, что состояние распреде-

ленных объектов Globe может раздельно храниться и реплицироваться на не-

скольких машинах.

Важно так структурировать наше обсуждение, чтобы иметь возможность срав-

нивать различные системы. По этой причине каждая из систем рассматривается

в отдельном разделе, который начинается с обзора наиболее важных концепций

системы, а именно ее объектной модели и основных служб, которые она поддер-

живает. Затем идет обсуждение семи принципов реализацирг системы: связи, про-

цессов, именования, синхронизации, непротиворечивости и репликации, отказо-

устойчивости, защиты.

Преимущество подобной структуры в том, что мы можем провести детальное

сравнение различных систем, рассматриваемых в разных разделах. С другой сто-

роны, поскольку основные аспекты этих принципов мы уже обсудили в первой

части книги, нам осталось описать лишь некоторые дополнительные моменты,

а скорее даже детализацию этих ОСРЮВ. Однако эти детали помогут нам понять,

как на самом деле работает каждая из систем и каким образом сравнивать их ме-

жду собоР!.

Существует множество книг, посвященных распределенным системам объек-

тов.

Несложный обзор CORBA и DCOM приводится в

[333].

В [138] системы

CORBA и DCOM вместе с Java RMI также используются в качестве примеров,

причем основное внимание уделяется нескольким прирщипам, лежащим в осно-

ве распределенных объектов. Как благодаря технологии распределенных объек-

тов можно гибко строить системное программное обеспечение, рассказывается

[209].

9.1.

CORBA

Мы начнем изучение распределенных систем объектов с рассмотрершя

обобщен-

ной архитектуры брокера

объектных

запросов (Common Object Request Broker

Architecture,

CORBA). Как следует из названия, CORBA

—

это не столько распре-

деленная система, сколько ее спецификация. Подобные спецификации разра-

ботаны группой управления объектами {Object Management Group, OMG), не-

коммерческой организацией, в которую входят более 800 членов, в основном

промышленных компаний. Основной целью OMG при разработке CORBA было

создание распределенной системы, способной преодолеть большинство проблем

межоперационной совместимости при интеграции сетевых приложений. Первые

спецификации CORBA появились в начале 90-х годов. В настоящее время широ-

ко распространена реализация CORBA версии 2.4, начинают появляться первые

образцы систем CORBA версии 3.