Теорія ймовірностей та математична статистика

Подождите немного. Документ загружается.

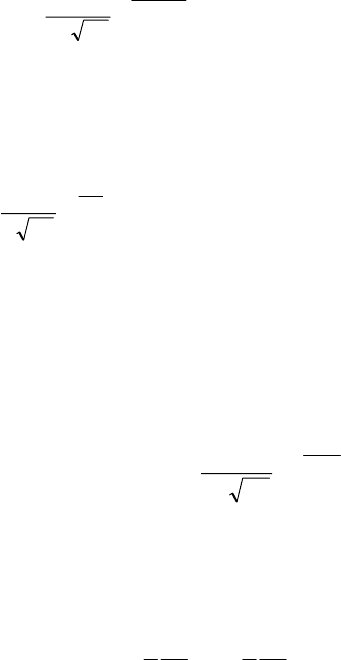
141

Вправи для самостійного розв’язування

5.14.

Із нормально розподіленої сукупності з

σ=DX

зробле-

но вибірку обсягом n. Знайти оцінку для МХ. Перевірити її на не-

зміщеність, ефективність та обґрунтованість.

5.15.

Із нормально розподіленої сукупності з MX = a зроблено

вибірку обсягом n. Знайти оцінку для DХ. Перевірити її на не-

зміщеність, ефективність та обґрунтованість.

5.16.

Із сукупності, розподіл у якій задається щільністю

()

πσ

µ−

−

зроблено вибірку обсягом n. Знайти

оцінку для

і перевірити її на незміщеність, ефективність та об-

ґрунтованість (значення

відоме).

5.17.

Із напівнормально розподіленої сукупності зроблено ви-

бірку обсягом n. Знайти оцінку для

. Перевірити оцінку на не-

зміщеність, ефективність та обґрунтованість, якщо

()

=xf

2σ

−

πσ

.0>x

5.18.

Із сукупності зі щільністю:

()

⎪

⎩

⎪

⎨

⎧

≥

µ−−

µ. якщо ,0

µ якщо ,

,xae

зроблено вибірку обсягом n. Знайти оцінки для

. i

5.19.

Із сукупності зі щільністю:

()

⎪

⎩

⎪

⎨

⎧

≤

πσ

⎟

⎠

⎞

⎜

⎝

⎛

µ−

−

. x

, xe

0 якщо ,0

0 якщо ,

зроблено вибірку обсягом n. Знайти оцінки для

. i

σµ

5.20.

Із сукупності, яка має подвійний розподіл Пуассона,

зроблено вибірку обсягом n. Знайти оцінки параметрів

, i

якщо

()

mXP

−−

+==

,....1,0

5.21

. Із сукупності, яка має поліноміальний закон розподілу,

зроблено вибірку обсягом r. Знайти оцінки для параметрів

142

,,...,,

21 s

ppp

якщо

(

)

mXmXmXP

,...,,

2211

()

....

ppp

∏

5.22. Із сукупності, розподіленої за законом Паскаля, зроблено

вибірку обсягом

. Знайти оцінку для параметра

, якщо

() ()

ppCmXP −==

−+

,....1,0

5.23. Із сукупності, розподіленої за біноміальним законом

зроблено вибірку обсягом

. Знайти оцінку для параметра

і по-

казати, що вона незміщена, ефективна та обґрунтована, якщо

() ()

ppCmXP

−

−==

.,...,1,0 nm

5.24. Із сукупності зі щільністю

()

α−−

xpp

зроблено вибірку обсягом

. Знайти оцінку для параметра α і

показати, що вона має додатне зміщення. Усунувши зміщення,

переконатися в тому, що така оцінка асимптотично ефективна.

5.25. Із сукупності, розподіленої показниково, зроблено вибір-

ку обсягом

. Знайти оцінку для параметра ,

ліквідувати змі-

щення і перевірити, чи буде здобута оцінка ефективною.

5.26. Із сукупності зі щільністю

()

(

)

α≥=

α−−

xaexf

зроблено

вибірку обсягом

.,...,,

21 n

XXX

Як оцінка параметра

пропону-

ється

{}

.min

X=α

Чи буде ця оцінка:

а) незміщеною (якщо ні, то знайти незміщену оцінку); б) об-

ґрунтованою?

5.27. Із рівномірно розподіленої сукупності зроблено вибірку

обсягом

.,...,

21 n

XXX

Як оцінка довжини інтервалу

−

пропо-

нується

VZh −=

де

{

}

{

}

.minV ,max

XXZ ==

Чи буде ця оцінка

незміщеною ?

5.28. Під час перевірки 400 лампочок середній строк їх горін-

ня становив 1220 год. Оцінити з надійністю

95,0

математичне

сподівання тривалості горіння, якщо

год і в сукупності ви-

конується нормальний закон розподілу.

5.29. На основі 100 спостережень було визначено, що в серед-

ньому для виробництва деталі потрібно 5,5 с, а

.89,2

Вважа-

ючи, що тривалість виготовлення деталі розподілена нормально,

143

знайти інтервальні оцінки для

i σa

з надійністю 0,96 і 0,98 від-

повідно.

5.30. Систематичні помилки вимірювального приладу дорів-

нюють нулю, а випадкові розподілені нормально з

м. Пот-

рібно, щоб абсолютне значення різниці між здобутим результа-

том і справжнім її значенням не перевищувало 10 м. Визначити, з

якою ймовірністю ця вимога виконуватиметься, якщо береться

середнє арифметичне

вимірювань і

= 4, 9, 16, 25.

5.31. У результаті вимірювання максимальної ємності 20 кон-

денсаторів дістали такі числові характеристики:

пф, 47,4

.пф 0121,0

Порівняти точність оцінки матетичного сподіван-

ня

за допомогою

з надійністю

95,0

, скориставшись нор-

мальним законом розподілу і законом розподілом Стьюдента.

5.32. У ВТК виміряно діаметри 200 валів, виготовлених одним

верстатом-автоматом. При цьому здобуто такі числові характерис-

тики відхилення розмірів від номіналу:

мкм,

.мкм 25,90

За допомогою асимптотично нормального розподілу знайти інте-

рвальні оцінки для математичного сподівання та дисперсії з на-

дійністю

.99,0=γ

5.33. Для деякої партії втулок потрібно визначити відсоток

браку. Вибірка обсягом

500

дала 30 дефектних виробів. З на-

дійністю

99,0=γ

визначити межі для частки (у відсотках) браку у

всій партії.

5.34. Як оцінку відстані до навігаційного знака беруть середнє

арифметичне незалежних вимірювань, що їх виконали

дальномі-

рів. Похибки вимірювання розподілені нормально з

10 i 0

=σ

м.

Скільки потрібно дальномірів, щоб абсолютна величина похибки

вимірювання відстані з імовірністю 0,96 не перевищувала 15 м?

5.3. ПЕРЕВІРКА СТАТИСТИЧНИХ ГІПОТЕЗ

Статистичною називається гіпотеза, яка стосується виду

або параметрів розподілу випадкової величини і яку можна пере-

вірити на підставі результатів спостереження у випадковій вибір-

ці. Перевіряючи статистичні гіпотези за результатами випадкової

вибірки, завжди ризикують прийняти хибне рішення. Але в тако-

му можна обчислити ймовірність прийняття хибного рішення і,

якщо вона мала, ризик помилки

буде невеликим. Помилки, яких

можна припуститися, бувають двох родів. Помилка першого роду

полягає в тому, що гіпотеза перевірювана

відхиляється, тоді

як вона правильна. Помилка другого роду полягає у тому, що гі-

144

потеза

приймається, тоді як вона хибна, а правильною є деяка

гіпотеза

Ця гіпотеза, яка протиставляється гіпотезі

нази-

вається

альтернативною. При цьому, хоча множина альтерна-

тивних гіпотез може бути нескінченною, висувається тільки одна

альтернативна гіпотеза

Статистичні гіпотези поділяються на

прості і складні.

Проста гіпотеза однозначно визначає закон ро-

зподілу випадкової величини. Для побудови статистичного кри-

терію, який дає змогу перевірити деяку гіпотезу

необхідно

вибрати

статистичну характеристику гіпотези

— деяку ви-

біркову функцію, визначити допустиму ймовірність помилки

першого роду

(рівень значущості), сформулювати альтернати-

вну гіпотезу

знайти критичну область

для статистичної ха-

рактеристики, щоб мінімізувати ймовірність помилки другого

роду. Критична область

— це така множина значень

, що ко-

ли

,GQ ∈

то гіпотеза

відхиляється на користь гіпотези

Критична область визначається так, щоб імовірність потрапляння

в неї статистичної характеристики за умови, що правильна гіпо-

теза

дорівнювала

— заданому рівню значущості, тобто

()

α=∈

HGQP

Крім того, необхідно, щоб

(

)

/ HGQP

∈ була ма-

ксимальною, тобто ймовірність помилки другого роду має бути

мінімальною. Останнє співвідношення називається

вимогою ма-

ксимізації потужності критерію

, який виражає ймовірність то-

го, що не буде допущено помилки другого роду.

Статистичні гіпотези поділяються на

параметричні і непа-

раметричні

. Параметричні гіпотези передбачають, що вигляд

закону розподілу відомий і перевірка зводиться до перевірки зна-

чень невідомих параметрів.

У разі, коли гіпотези

i HH

прості і розглядається непере-

рвна випадкова величина, то побудова критерію ґрунтується на

теоремі Неймана—Пірсона.

Коли гіпотеза, що перевіряється, і альтернативна їй гіпотеза є

простими гіпотезами виду відповідно

1100

: i :

θ=θθ=θ

і як-

що

()

021

,,...,,

xxxL

(

)

121

,,...,,

xxxL

— функції правдоподібнос-

ті, які знайдено за умови, що правильна відповідно гіпотеза

або

, то існує найпотужніший критерій для гіпотези

сто-

совно альтернативної гіпотези

Критична область і статис-

тична характеристика гіпотез визначаються нерівністю:

()()

,,,...,,,,...,,

021121

θ≥θ

xxxcLxxxL

де

— додатна стала, значення

якого залежить від рівня значущості.

145

Якщо принаймні одна з гіпотез

або

не є простою, не-

рівність не можна застосувати. У цьому разі можна побудувати

критерій, що ґрунтується на відношенні функцій правдоподіб-

ності (знову вважається, що розподіл у сукупності непере-

рвний).

Припустимо, що змінна

має щільність виду

(

)

,,...,,,

21 r

θθθ яка залежить від

параметрів, а гіпотеза

подається у вигляді:

ω∈θ

, де

— вектор з

компонентами

()

ω≤

a ,rs

— деяка підмножина

Ω

усіх можливих значень па-

раметра. Гіпотеза

.\:

ωΩ∈θH

Для побудови критерію визна-

чають функцію правдоподібності

(

)

θ,,...,,

21 n

xxxL

, а далі знахо-

дять її максимуми для випадків, коли

. i Ω∈θω∈θ

Далі

складають відношення:

(

)

()

,,...,,max

=λ

Ω∈θ

ω∈θ

xxxL

Значення

завжди належить інтервалу

(

)

.1;0

Чим ближче

до

одиниці, тим правдоподібніша гіпотеза

і навпаки: чим ближ-

че значення

до нуля, тим більше підстав для відхилення

Критична область для

лівостороння. Вона визначається з умо-

ви:

()

α=λ<λ

Якщо відомий закон розподілу для

, то можна знайти грани-

цю критичної області для заданого критерію. Критерії, що ґрун-

туються на відношенні функцій правдоподібності, асимптотично

найпотужніші.

Розглянемо основні параметричні статистичні критерії.

А. Перевірка гіпотези про математичне сподівання

нормально розподіленої сукупності

Якщо дисперсія сукупності відома і дорівнює

, то при

.00

: aaH

за статистичну характеристику береться

вибіркова функція

−

Критична область визначається

залежно від значення

a і відповідно до рівня значущості

. Мо-

жливі три випадки.

146

1. Якщо

> то критична область правостороння. Її межа

визначається за умовою:

()

=≥

∫

∞

−

dtezZP

(

)

α=Φ−=

z5,0

. Тоді

()

.5,0

α−Φ=

−

2. Якщо

< , то критична область лівостороння, =

(

)

.5,0

α−Φ−=

−

3. Якщо

≠ то критичній області належать значення

. i

αα

−≤≥ zzzz

При цьому

5,0

⎟

⎠

⎞

⎜

⎝

⎛

−Φ=

−

Коли дисперсія сукупності невідома, то для перевірки гіпотези

використовується вибіркова функція

−

= n

розподіле-

на за законом Стьюдента з

n – 1 ступенями волі. Вигляд критич-

ної області визначають так само, як і в попередніх випадках, а

межу знаходять за допомогою таблиць розподілу Стьюдента з ві-

дповідною кількістю ступенів волі. Якщо

n > 20, то розподіл

Стьюдента апроксимується нормальним розподілом з нульовим

математичним сподіванням і одиничною дисперсією.

Б. Перевірка гіпотези про дисперсію

нормально розподіленої сукупності

Коли рівень значущості дорівнює

, перевіримо гіпотезу

: σ=σH

за альтернативної гіпотези

. :

σ=σH

Якщо справ-

джується гіпотеза, яка перевіряється, то вибіркова функція

має розподіл

з n – 1 ступенями волі. Як і в попередніх

випадках, вигляд критичної області визначається значенням

Межі критичної області визначаються так:

якщо

σ>σ

то критична область G правостороння,

()

;

αχ=

якщо

σ<σ

то критична область G лівостороння,

()

α−χ=

якщо

σ=σ

то критична область двостороння. Їй нале-

жать значення

≤

≥

де

a ,

⎟

⎠

⎞

⎜

⎝

⎛

χ=

⎟

⎠

⎞

⎜

⎝

⎛

−χ= uu

147

В. Перевірка гіпотези про істотність

різниці математичних сподівань

двох нормально розподілених сукупностей

Нехай задано дві нормально розподілені сукупності з однако-

вими дисперсіями, але, можливо, із різними математичними спо-

діваннями. Із цих сукупностей зроблено вибірки обсягом відпові-

дно

i nn

. Числові характеристики вибіркових сукупностей:

. , i ,

SXSX

Якщо позначити різницю

δ=−

то гіпотезу

δ=δ

можна перевірити за допомогою вибіркової функції

2121

021

⎟

⎠

⎞

⎜

⎝

⎛

−+

δ−−

nnnn

snsn

Якщо гіпотеза

правильна, то Z має

розподіл Стьюдента з

−+

ступенями волі. Залежно від

значення

δ у альтернативній гіпотезі визначають критичну

область за допомогою таблиць розподілу Стьюдента, а в разі

великих значень

i nn

— за допомогою таблиць функції Ла-

пласа.

Г. Перевірка гіпотези про рівність дисперсій

двох нормально розподілених сукупностей

Нехай задано дві нормально розподілені сукупності. На підс-

таві вибірок обсягом

i nn

із цих сукупностей потрібно переві-

рити гіпотезу

: σ=σH за альтернативної гіпотези

: σ>σH .

Статистичною характеристикою для перевірки гіпотези

буде

вибіркова функція

−

При побудові відношення чисе-

льник має бути не меншим від знаменника. Якщо гіпотеза

правильна, то вибіркова функція

F має розподіл Фішера з

1 i 1

−−

ступенями волі. Критична область G правостороння

і визначається умовою

(

)

α=≥

fFP

148

Д. Критерій дисперсійного аналізу

Нехай задано k нормально розподілених сукупностей з одна-

ковими дисперсіями і, можливо, різними математичними споді-

ваннями. Із кожної сукупності зроблено вибірку обсягом

Пе-

ревіряється гіпотеза

.... :

210

aaaH

=== Статистичною характе-

ристикою гіпотези є вибіркова функція

()

∑∑

∑

−

iij

nXX

де

— j-те значення випадкової величини ;

∑

;

∑

;

∑

. Якщо гіпотеза

правильна, то вибіркова

функція має розподіл Фішера з k – 1 i n – k ступенями волі. Кри-

тична область правостороння і визначається так, як це було зроб-

лено в попередньому пункті.

Крім наведених параметричних критеріїв перевірки статисти-

чних гіпотез розглядаються критерії для перевірки непараметри-

чних статистичних гіпотез, сутність яких можна схарактеризува-

ти так.

Якщо маємо вибірку обсягом n, то чи правильним є тверджен-

ня, що її зроблено із сукупності з даною функцією розподілу

()

Критерій

Пірсона

Критерій ґрунтується на порівнянні теоретичних і емпіричних

частот. Нехай область реалізацій випадкової величини розбито на

k інтервалів, частоти яких дорівнюють

∑

Якщо гіпоте-

за про закон розподілу в сукупності правильна, то можна обчис-

лити ймовірності

(

)

iii

xXxPp

<≤=

−

тобто ймовірність потрап-

ляння випадкової величини на i-й інтервал. Теоретичні частоти

потрапляння нa цей інтервал можна розглядати як математичне

сподівання компонентів випадкової величини, розподіленої за

поліноміальним законом:

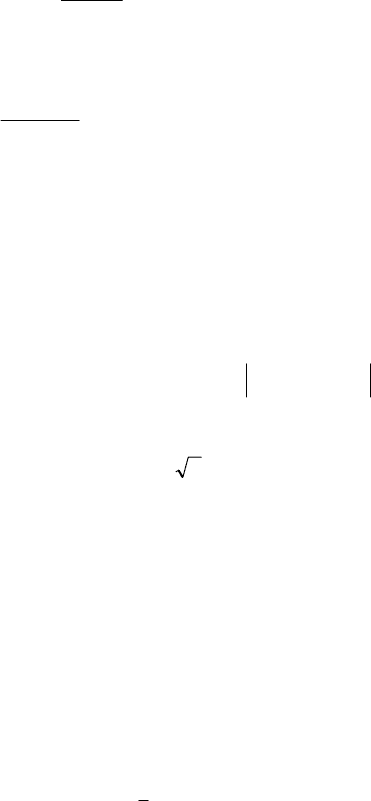
149

(

)

====

mXmXmXP ;...;;

2211

()

;...

ppp

∏

.,...,2,1 , kinpnMX

iii

′

Статистичною характеристикою гіпотези є вибіркова функція

()

∑

′

−

′

Якщо

∞

→n

, то вибіркова функція має розподіл

−

ступенями волі, де r — кількість параметрів, оцінки

для яких знайдено за вибірковими даними. Критична область для

статистичної характеристики правостороння.

Критерій Колмогорова

Критерій ґрунтується на порівнянні статистичної і теоретич-

ної функцій розподілу. Якщо

(

)

(

)

,max xFxFD

−=

∗

то при

∞→n

(

)

()

,1 λ−→λ≥

KDnP

де

() ( )

.0 ,1

>λ−=λ

∑

∞

λ−

За допомогою таблиць розподілу Ко-

лмогорова визначається правостороння критична область.

Приклади розв’язування задач

Приклад 1

. Побудувати найпотужніший критерій для переві-

рки гіпотези

: aaH

за альтернативної гіпотези

: aaH

, якщо

вибірку обсягом n зроблено з нормально розподіленої сукупності

з дисперсією, що дорівнює

Дібрати таке значення С, при

якому

= 0,02, якщо

.25 ,9 ,12 ,10

==σ== naa

Яка з гіпотез

приймається, якщо

9,10

Розв’язання. Застосуємо нерівність із теореми Неймана — Пі-

рсона:

()

(

)

.,,...,,,,...,,

021121

axxxcLaxxxL

≥ Побудуємо функції прав-

доподібності:

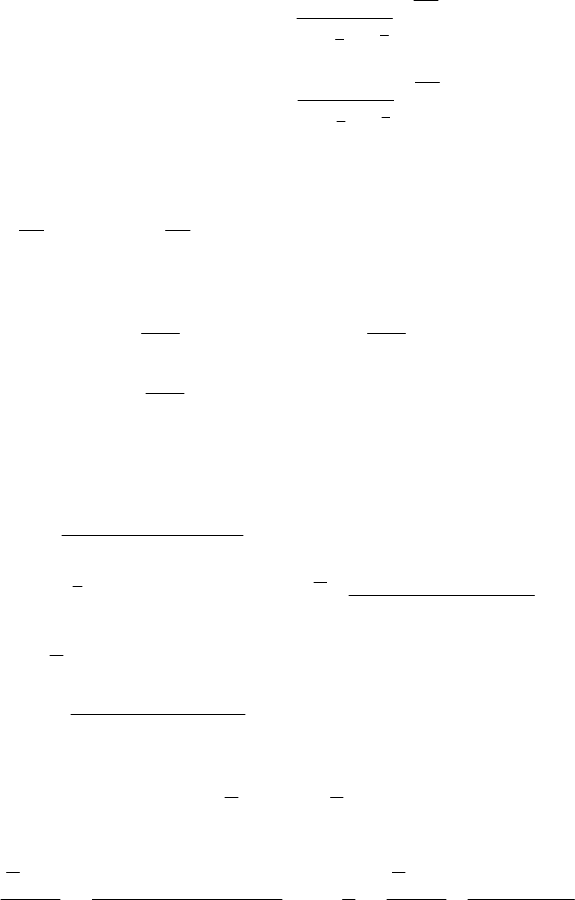
150

()

,,...,,

1.21

∑

−

σπ

eaxxxL

()

,,...,,

0.21

∑

−

σπ

eaxxxL

Підставимо функції правдоподібності в нерівність і виконаємо

спрощення скороченням сталих множників. Дістанемо нерівність

() ()

∑∑

−

−−

−

≥

axax

Cee

, яку прологарифмуємо і виконаємо

низку перетворень:

()

Cax

≥−

−

∑

()

∑

−

;

()()

;ln

Caxax

≥

⎟

⎠

⎞

⎜

⎝

⎛

−−−

∑∑

;ln222

Cnaxaxnaxax

σ≥−+−+−

∑∑∑∑

====

(

)

()

ln2

aanC

−

−+σ

≥

∑

бо за умовою

> Після заміни

xnx

∑

остаточно дістанемо

(

)

()

ln2

aan

aanC

−

−+σ

≥

Отже, статистичною характеристикою гіпотези є вибіркова фун-

кція

а критичною областю для неї — множина значень, не мен-

ших за

()

ln2

aan

aanC

−

−+σ

Щоб дібрати значення С, потрібно знати

закон розподілу вибіркової функції. Якщо справджується гіпотеза

, то вибірку зроблено з нормально розподіленої сукупності з

.9 i 10

=σ=a

Тоді

.36,0 a ,10

XDXM

Центруємо і нормуємо

вибіркову функцію, щоб застосувати таблиці функції Лапласа. Ана-

логічні перетворення виконуємо з правою частиною нерівності:

()

;

250

10014425ln18

6,0

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

−+

≥

− CX

100ln18

6,0

10 +

≥

− CX

Кри-

тична область правостороння, тому її межа

()

;5,0

α−Φ=

−