Tong W. Wind Power Generation and Wind Turbine Design

Подождите немного. Документ загружается.

Optimized Gearbox Design 525

It also emphasizes the importance of isolating the gearbox from the parasitic forces

imposed by the turbine on its rotor support.

The volumetric concept facilitates the synthesis of the initial design of gears

rather than using an analytical/iterative approach. It helps to optimise the overall

size and weight of gears by showing the value of using lower ratios in the high

torque low speed stages of high ratio applications, particularly when epicyclic

trains are involved. Ultimately, all stress criteria are subject to arbitrary limits

embodying a string of "factors of ignorance" which tend to be treated as virtual

constants. Ten such factors, with a 5% increase in each, would reduce permissible

load by 40%!

This page intentionally left blank

CHAPTER 16

Tower design and analysis

Biswajit Basu

Trinity College Dublin, Ireland.

This chapter addresses some of the design and analysis issues of interest to struc-

tural and wind engineers involved in ensuring the serviceability and survivability

of wind turbine towers. Wind turbine towers are ﬂ exible multi-body entities con-

sisting of rotor blades which collect the energy contained within the wind, and the

tower which supports the weight of the rotor system and nacelle and transfers all

gravity and environment loading to the foundation. Two themes on the design and

analysis aspects of the tower have been presented. The ﬁ rst is the mathematical

representation of the behaviour of wind turbine towers when subjected to wind

loading and the second is the suppression of the vibrations caused by this wind

action. The ﬁ rst theme focuses on a series of mathematical models representing

the rotor blades, the tower with the added mass of the nacelle, and the coupled

rotor blade and tower system which are used to determine the free and forced

vibration characteristics of the structure. Response estimation for the rotating

blades includes the effects of centrifugal stiffening, dynamic gravity effects due

to rotation and rotationally sampled turbulence. A gust factor approach is also

presented for design of the wind turbine towers. The second theme considers the

mitigation of vibrations under dynamic wind action by adding energy dampers to

the system, and ﬁ nding the optimal properties of these dampers in order to maxi-

mise the reduction of vibration. Modelling and analysis of offshore towers have

also been discussed.

1 I ntroduction

With the exponential growth in the wind energy market, turbines with larger rotor

diameter and hence taller towers are becoming more common. This has a crucial

impact on the design and analysis of wind turbine towers. The primary function

of the wind turbine tower is to elevate the turbine rotor for a horizontal axis wind

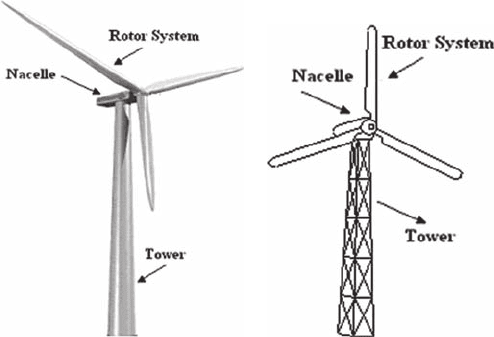
528 Wind Power Generation and Wind Turbine Design

turbine (HAWT) and support the mechanical and electrical system housed in the

nacelle. Wind speed increases with altitude and also tends to become less turbu-

lent. As a result more energy can be extracted with taller towers. However, this

comes at a price of higher cost of construction and installation. Choice of tower

height is based on a tradeoff between increased energy production at a particular

site and the increase in the cost of construction.

The principal types of towers currently in use are the free standing type using

steel tubes ( Fig. 1a ), lattice (or truss) towers ( Fig. 1b ) and concrete towers. For

smaller turbines, guyed towers are also used. Tower height is typically 1–1.5

times the rotor diameter. Tower selection is greatly inﬂ uenced by the character-

istics of the site. The stiffness of the tower is a major factor in wind turbine

system dynamics because of the possibility of coupled vibrations between the

rotor and tower. In addition, there are several other factors which affect the selec-

tion of the type of tower and its design, such as the mode of erection and fabrica-

tion, sizes of crane required for construction, noise, impact on avian population

and aesthetics. Among the different type of towers, tubular towers are more com-

mon and they are also preferable due to aesthetics and in minimizing impact on

avian population.

One of the primary considerations in the tower design is the overall tower stiff-

ness, which in turn affects its natural frequency. From a structural dynamics point

of view, a stiff tower whose fundamental natural frequency is higher than that of

the blade passing frequency (rotor’s rotational speed times the number of blades)

is preferable. This type of tower has the advantage of being relatively unaffected

by the motions of the rotor-turbine itself. However, the cost may be prohibitive due

to a larger mass and hence more material requirement.

(a) (b)

Figure 1: (a) Free standing tubular wind turbine tower; (b) lattice wind turbine

tower.

Tower Design and Analysis 529

Towers are usually classiﬁ ed based on the relative natural frequencies of the

tower and the rotor blades. Opposite to the stiff towers, soft towers are those whose

fundamental natural frequency is lower than the blade passing frequency. A further

subdivision differentiates a soft and a soft–soft tower. A soft tower’s natural fre-

quency is above the rotor frequency but below the blade passing frequency while

a soft–soft tower has its natural frequency below both the rotor frequency and the

blade passing frequency. These kinds of towers (soft and soft–soft) are generally

less expensive than the stiffer ones, since they are lighter. However, they require

particular attention and need careful dynamic analysis of the entire system to

ensure that no resonances are excited by any motions in the rest of the turbine.

2 Analysis of towers

2.1 Tower blade coupling

Design engineers are interested in understanding and analyzing the coupled dynam-

ics of wind turbine towers with associated components, especially with proliferation

of such systems worldwide for renewable energy production. As wind turbines are

becoming larger in size and are being placed in varying global wind environments,

knowledge of the dynamic behaviour is important. The behaviour of the subcompo-

nents of the system (the tower and rotor blades) as well as the dynamic interaction of

those components with each other is vital to ensure the serviceability and survivabi-

lity of such expensive power generating infrastructure. Following a conventional and

simpliﬁ ed design analysis, the mass of the components (nacelle and rotor blades)

can be simply lumped at the top of the tower, and as long as the fundamental fre-

quencies of the tower and blades are far apart, a stochastic forced vibration analysis

could be carried out. While the simplicity of this is attractive, the ﬂ exibility of large

rotor systems may result in either economically inefﬁ cient design due to the conser-

vatism required to accommodate the uncertainties of component interaction or an

unsafe design due to ignoring the coupling effects.

Published literature available regarding the dynamic interaction of wind turbine

components, especially from the point of view of the structural design of the tower

with the interaction of the mechanical rotor blade system is growing. Harrison

et al. [ 1 ] state that the motion of the tower is strongly connected to the motion of

the blades, as the blades transfer an axial force onto the low speed drive shaft

which is ultimately transferred into the nacelle base plate at the top of the tower.

The dynamic characteristics of a multi-body system have traditionally been

determined by the substructure synthesis or component mode synthesis method

[ 2 , 3 ]. In coupled analyses, it is ﬁ rst necessary to obtain the free vibration charac-

teristics of all sub-entities, prior to dynamic coupling. The free vibration proper-

ties of a tower carrying a rigid nacelle mass at the top may be evaluated by

techniques such as the discrete parameter method, the ﬁ nite element method or by

using closed form solutions. The discrete parameter method was used by Wu and

Yang [ 4 ] in a study on the control of transmission towers under the action of sto-

chastic wind loading. Lavassas et al. [ 5 ] also used this technique to assess the

530 Wind Power Generation and Wind Turbine Design

accuracy and reliability of more computationally expensive ﬁ nite element analy-

ses of wind turbine tower. Recent studies using the ﬁ nite element technique for

free vibration analyses of structures in wind engineering include Bazeos et al. [ 6 ]

and Dutta et al. [ 7 ]. Murtagh et al. [ 8 ] derived an expression in closed form to

yield the eigenvalues and eigenvectors of a tower-nacelle system comprising of a

prismatic cantilever beam with a rigid mass at its free end.

2.2 Rotating blades

The free vibration properties of realistic wind turbine blades are computationally

more difﬁ cult to obtain, and models are usually mathematically complicated due

to the complex geometry of the blade and the effects of blade rotation. Baumgart

[ 9 ] used a combination of ﬁ nite elements and virtual work, accounting for the

complex geometry of the blade to obtain the modal parameters. Naguleswaran [ 10 ]

proposed an approach to determine the free vibration characteristics of a spanwise

rotating beam subjected to centrifugal stiffening. This model [ 10 ] can be used in

many industrial ﬁ elds, such as wind turbine blades, aircraft rotor blades and tur-

bine rotor blades. Naguleswaran [ 10 ] and Banerjee [ 11 ] both used the Frobenius

method to obtain the natural frequencies of spanwise rotating uniform beams for

several cases of boundary conditions. Chung and Yoo [ 12 ] used the ﬁ nite element

method to obtain the dynamic properties of a rotating cantilever, whereas Lee

et al. [ 13 ] carried out experimental studies on the same. All studies indicate that

the natural frequencies rise as the rotational frequency of the blade increases. Vari-

ous software codes have been developed by engineers to dynamically analyse

the various components of a wind turbine tower. Buhl [ 14 ] presented guidelines

for the use of the software code ADAMS in free and forced vibrations of wind

turbine towers.

Under the action of rotation, the free vibration parameters of the blades are

affected by two axial phenomena. The ﬁ rst is centrifugal stiffening and the second

is blade gravity (self weight) effects. In order to ﬁ nd the free vibration properties

of the blades, each blade can be discretized into a lumped parameter system com-

prising of ‘ n ’ degrees of freedom. The eigenvalues of a blade undergoing ﬂ apping

motion may be obtained from the eigenvalue analysis:

BBB

[] []=0KMw

′

−

(1 )

where

BBBG

[][ ]K=K K

′

represents the modiﬁ ed stiffness matrix due to the geo-

metric stiffness matrix [ K

], accounting for the effect of axial load, w

is the

natural frequency, [ K

] is the ﬂ exural stiffness matrix and [ M

] is the mass matrix.

The mass matrix may be formulated as a diagonal matrix with the mass m

at each

discrete node i .

The geometric stiffness matrix contains force contributions due to blade rota-

tion which are always tensile, and contributions from the self weight of the blade,

which may be either tensile or compressive, depending on blade position. The

geometric stiffness matrix is

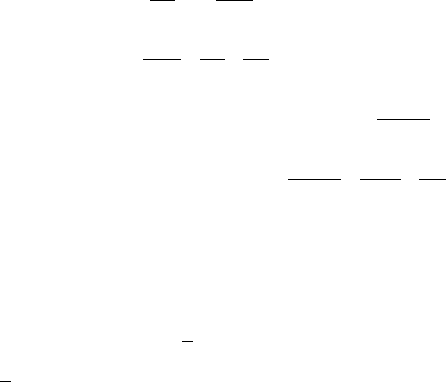
Tower Design and Analysis 531

112

…0

[]

nnn

NNN

lll

NNN

lll

−

−−

−

⎡⎤

⎢⎥

−

⎢⎥

−

⎢⎥

−

⎢⎥

⎣⎦



(2 )

where N

is the axial force at node ‘ i ’ and l

is the length of beam segment between

the nodes ‘ i ’ and ‘ i + 1’. The magnitude of the tensile centrifugal axial force,

CT( x ), along the axis of a continuous blade, may be found from the expression

given by Naguleswaran [ 10 ] as

BBBHH

CT( ) 0.5 ( 2 2 )xmLLRRxx=Ω+ −−

(3 )

where

m represents the mass per unit length of the blade, Ω is the rotational

frequency of the blade, and x is the distance along the blade from the hub. This

continuous force distribution is discretized into nodal values (CT

) and used to

form the geometric stiffness matrix. The component of nodal blade gravity force

(self weight), G

, acting axially may be obtained from geometry and depends on

the angle q that the longitudinal axis of the blade makes with the horizontal global

axis, in the plane of rotation. Values of N

are obtained from the expression:

iii

CTNG=±

(4 )

with the sign convention that tensile forces are positive and compressive forces

are negative.

2.3 Forced vibration analysis

Forced vibration analyses of structures may either be carried out in the time or

frequency domain, with each having its own distinct merits. Analysis through the

time domain allows for the inclusion of behavioural non-linearity and response

coupling. Due to limited availability of actual input time-histories as measured in

the ﬁ eld, the designer has to generate relevant artiﬁ cial time-histories using widely

published spectral density functions. The method for generating the artiﬁ cial time-

histories can be divided into three categories, the ﬁ rst based on a fast Fourier trans-

form (FFT) algorithm, the second based on wavelets and other time–frequency

algorithms and the third based on time-series techniques such as Auto-Regressive

Moving Average (ARMA) method. Suresh Kumar and Stathopoulos [ 15 ] simu-

lated both Gaussian and non-Gaussian wind pressure time-histories based on the

FFT algorithm. Kitagawa and Nomura [ 16 ] recently used wavelet theory to gen-

erate wind velocity time-histories by assuming that eddies of varying scale and

strength may be represented on the time axis by wavelets of corresponding scales.

532 Wind Power Generation and Wind Turbine Design

In an investigation on the buffeting of long-span bridges, Minh et al. [ 17 ] used

the digital ﬁ ltering ARMA method to numerically generate time-histories of wind

turbulence.

In simulating drag force time-histories on the tower, information on spatial cor-

relation, or coherence is necessary to be included. Coherence relates the similarity

of signals measured over a spatial distance within a random ﬁ eld. Coherence is of

great importance, especially if gust eddies are smaller than the height of a struc-

ture. Some of the earliest investigations into the spatial correlation of wind forces

were carried out by Panofsky and Singer [ 18 ] and Davenport [ 19 ] and later aug-

mented by Vickery [ 20 ] and Brook [ 21 ]. Recent publications involving lateral

coherence in wind engineering include Højstrup [ 22 ], Sørensen et al. [ 23 ] and

Minh et al. [ 17 ].

2.4 Rotationally sampled spectra

In order to simulate the drag force time-histories on the rotating blades, a special

type of wind velocity spectrum is needed. Connell [ 24 ] reported that a rotating

blade is subjected to an atypical ﬂ uctuating wind velocity spectrum, known as

a rotationally sampled spectrum. Due to the rotation of the blades, the spectral

energy distribution is altered, with variance shifting from the lower frequencies

to peaks located at integer multiples of the rotational frequency. Kristensen and

Frandsen [ 25 ], following on from work by Rosenbrock [ 26 ], developed a simple

model to predict the power spectrum associated with a rotating blade, and this was

signiﬁ cantly different to a spectrum without the rotation considered. Though liter-

ature on this topic is limited, Madsen and Frandsen [ 27 ], Verholek [ 28 ], Hardesty

et al. [ 29 ] and Sørensen et al. [ 23 ] are some relevant references on this topic.

Rotationally sampled spectra are used to quantify the energy as a function of

frequency for rotor blades within a turbulent wind ﬂ ow for representing the redis-

tribution of spectral energy due to rotation. The required redistribution of spectral

energy can be achieved by identifying the speciﬁ c frequencies 1 Ω , 2Ω , 3 Ω , and

4 Ω ( Ω being the rotational frequency of the blades), and then deriving the Fourier

coefﬁ cients for those frequencies according to speciﬁ c standard deviation values.

These values can be obtained based on some measurements or assumption

related to the rotational turbulence spectra. Madsen and Frandsen [ 27 ] observed

that the peaks of redistributed spectral energy in a rotationally sampled spec-

trum tend to become more pronounced as distance increases along the blade,

away from the hub.

The typical rotationally sampled turbulence spectra are shown in Fig. 2 [ 30 ]. It

has been assumed for the spectra that the variance values increase by an arbitrary

value of 10%, for each successive blade node radiating out from the hub. It is also

assumed that 30% of the total variance at each node is localized into peaks at 1 Ω ,

2 Ω , 3Ω , and 4Ω (15%, 7.5%, 4.5% and 3% of the total energy is allocated to the

different peaks). Nodal ﬂ uctuating velocity time-histories with speciﬁ c energy–

frequency relationships can be simulated from the spectra in Fig. 2 using a discrete

Fourier transform (DFT) technique.

Tower Design and Analysis 533

Using the loading from the rotationally sampled spectra of turbulence and using

a mode-acceleration method, Murtagh et al. [ 31 ] estimated the wind-induced

dynamic time-history response of tapered rotating wind turbine blades. The mode-

acceleration method was initially implemented by Williams [ 32 ] and Craig [ 33 ]

reported that it has superior convergence characteristics compared to the mode-

displacement method. Singh [ 34 ] presented a method for obtaining the spectral

response of a non-classically damped system, based on the mode-acceleration

technique. Akgun [ 35 ] presented an augmented algorithm based on the mode-

acceleration method which has improved convergence for computation of stresses

in large models.

2.5 Loading on tower-nacelle

The tower can be modelled as a lumped mass multi-degree-of-freedom (MDOF)

ﬂ exible entity, which includes a lumped mass at the top of the tower, to represent

the mass of the nacelle and the effect of the blades. An eigenvalue analysis can be

performed to obtain the natural frequencies and mode shapes. As the tower-nacelle

is a MDOF system, it is convenient to obtain modal force time-histories associated

with each mode for analysis. This allows the spatial correlation or coherence of

drag forces along the height of the tower to be included. Nigam and Narayanan

[ 36 ] presented an expression for the modal ﬂ uctuating drag force power spectrum,

for a continuous line-like structure, which can be used following modiﬁ cation for

a discretized MDOF system [ 30 ].

The wind velocity auto and cross power spectral density (PSD) terms may be

evaluated as

() () ()coh(,;)

VVV

kkVklVl

SfSfSf klf=

(5 )

Figure 2 : Rotationally sampled turbulence spectra.

534 Wind Power Generation and Wind Turbine Design

with S

vkvk

( f ) and S

vkvk

( f ) being the velocity PSD functions at nodes k and l respec-

tively and coh( k , l ; f ) is the spatial coherence function between nodes k and l . The

terms S

vkvk

( f ) and S

vkvk

( f ) are functions of frequency f and may be calculated

using the Kaimal spectra [ 37 ]. A coherence function suggested by Davenport

[ 19 ], coh( k , l ; f ), which relates the frequency dependent spatial correlation between

nodes k and l , is represented as

coh( , ; ) exp

kl f

⎛⎞

−

=−

⎜⎟

⎝⎠

(6 )

where | k – l | is the spatial separation and L

is a length scale given by

(7 )

with

0.5( )

vvv=+

(8 )

and D is a decay constant. The ﬂ uctuating component of the modal force acting

on the tower may be obtained by employing the DFT technique. The mean nodal

drag force component is obtained by transforming the nodal mean drag force time-

histories into modal force time-histories using the modal matrix. The mean modal

drag force is added to the modal ﬂ uctuating component to obtain the total modal

drag force time-history.

2.6 Response of tower including blade–tower interaction

In order to couple the tower and rotating blades, equations of motion for the

tower that includes the blade shear forces is necessary to be considered. This is

represented by

{} {}

TT TB

[ ] () +[ ] () +[ ]{()}={ ()}+{ ()}

Mxt Cxt Kxt Ft Vt

 

(9 )

where [ M

], [ K

] and [ C

] are the mass, stiffness and damping matrices of the

tower-nacelle respectively, {()},{()},{()}xt xt xt



are the displacement, velocity and

acceleration vectors respectively, { F

( t )} is the total wind drag loading vector act-

ing on the tower and

{()}Vt

′

is the effective blade base shear vector transmitted

from the root of the rotating blades and acting at the top of the tower. The set of

equations cannot be solved directly in time domain as the base shear is dependent

on the motion of the tower (due to coupling) and hence is not known explicitly. An

alternative way to solve the equations is to convert the set into a set of algebraic

equations by FFT and subsequently solve by inverse FFT [ 30 ].

A numerical example [ 30 ] is presented for a steel wind turbine tower of height

60 m with three blades of rotor radius 30 m. The total mass of the nacelle and rotor

system is 19,876 kg. The average wind speed at the top of the tower is 20 m/s.

Figure 3 shows the displacement response time-history at the top of tower when