Трофимова Т.И. Курс физики

Подождите немного. Документ загружается.

Подставив в (220.5) значение к из

(220.6), найдем собственные функции:

Постоянную интегрирования А най-

дем из условия нормировки (216.3),

которое для данного случая запишется

в виде

В результате интегрирования полу-

чим

А —

Jy,

а собственные функции

будут иметь вид

I рафики собственных функции

(220.8), соответствующие уровням

энергии (220.7) при п=1,2, 3, приведе-

ны на рис. 300, а. На рис. 300, б изобра-

жена плотность вероятности обнаруже-

ния частицы на различных расстояни-

ях от «стенок» ямы, равная

|ф„(ж)|

(х)^)*(х)

для п= 1, 2 и 3. Из рисун-

ка следует, что, например, в квантовом

состоянии с п = 2 частица не может на-

ходиться в середине «ямы», в то время

как одинаково часто может пребывать

в ее левой и правой частях. Такое пове-

дение частицы указывает на то, что

представления о траекториях частицы

в квантовой механике несостоятельны.

Из выражения (220.7) вытекает, что

энергетический интервал между двумя

соседними уровнями равен

Например, для электрона при раз-

мерах ямы

— 10"

м (свободные элек-

троны в металле)

АЕ

Дж

10~

пэВ,

т. е. энергетические уровни

расположены столь тесно, что спектр

практически можно считать непрерыв-

ным. Если же размеры ямы соизмери-

мы с атомными

10~

м), то для

электрона

АЕ

та

10~

Дж

та

эВ,

т.е. получаются явно дискретные зна-

чения энергии (линейчатый спектр).

Таким образом, применение уравне-

ния Шредингера к частице в «потенци-

альной яме» с бесконечно высокими

«стенками» приводит к квантованным

значениям энергии, в то время как клас-

сическая механика на энергию этой ча-

стицы никаких ограничений не накла-

дывает.

Кроме того,

квантово-механическое

рассмотрение данной задачи приводит

к выводу, что частица «в потенциаль-

ной яме» с бесконечно высокими «стен-

ками» не может иметь энергию меньше

%Чъ

минимальной, равной

[см. (220.7)].

Наличие отличной от нуля мини-

мальной энергии не случайно и выте-

кает из соотношения неопределеннос-

тей. Неопределенность координаты Ах

частицы в «яме» шириной

/равна

Ах=

Тогда, согласно соотношению неопре-

деленностей

(215.1),

импульс не может

иметь точное, в данном случае нулевое,

значение. Неопределенность импульса

Ар?а—,

Такому разбросу значений

411

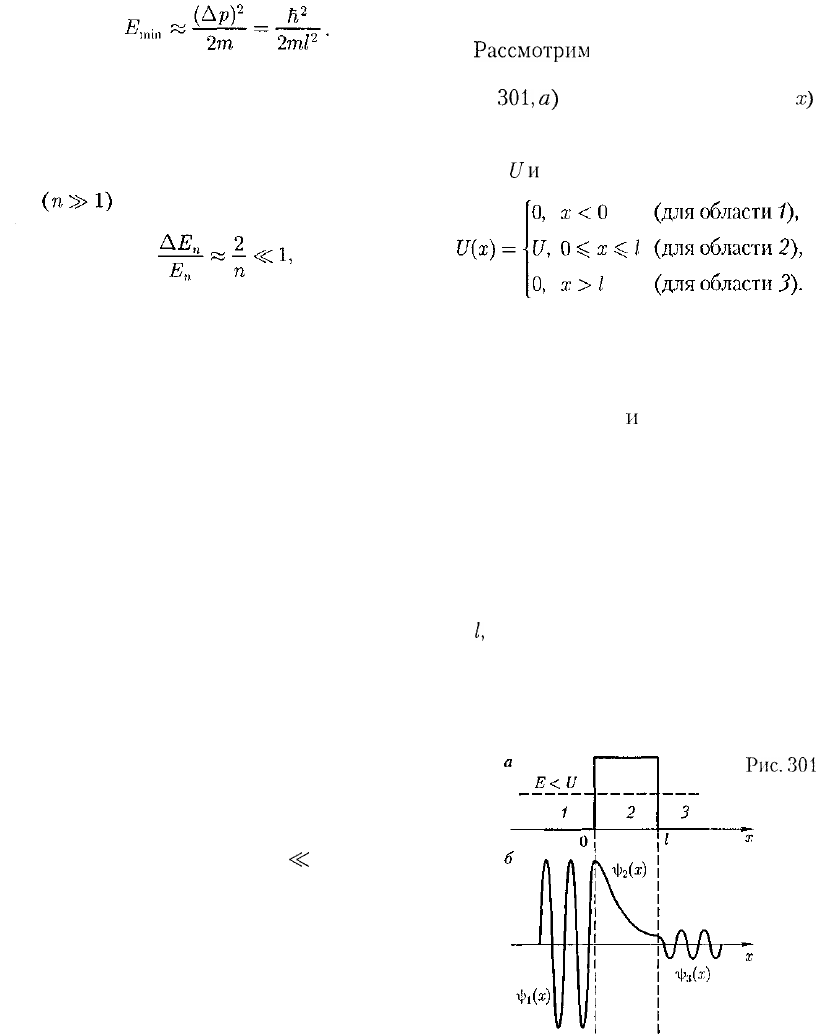
импульса соответствует кинетическая

энергия

Все остальные уровни (п > 1) име-

ют энергию, превышающую это мини-

мальное значение.

Из формул (220.9) и (220.7) следу-

ет, что при больших квантовых числах

т. е. соседние уровни расположены тес-

но: тем теснее, чем больше п. Если п

очень велико, то можно говорить о

практически непрерывной последова-

тельности уровней и характерная осо-

бенность квантовых процессов — диск-

ретность — сглаживается. Этот резуль-

тат является частным случаем принци-

па соответствия Бора (1923), соглас-

но которому законы квантовой механи-

ки должны при больших значениях

квантовых чисел переходить в законы

классической физики.

Более общая трактовка принципа

соответствия: всякая новая, более

общая теория, являющаяся развитием

классической, не отвергает ее полнос-

тью, а включает в себя классическую

теорию, указывая границы ее примене-

ния, причем в определенных предель-

ных случаях новая теория переходит в

старую. Так, формулы кинематики и

динамики специальной теории относи-

тельности переходят при v

<§;

с в форму-

лы механики Ньютона. Например, хотя

гипотеза да Бройля приписывает вол-

новые свойства всем телам, но в тех слу-

чаях, когда мы имеем дело с макроско-

пическими телами, их волновыми свой-

ствами можно пренебречь, т.е. приме-

нять классическую механику Ньютона.

§ 221. Прохождение частицы

сквозь потенциальный барьер.

Туннельный эффект

Рассмотрим

простейший потенци-

альный барьер прямоугольной формы

(рис.

301,

а)

для одномерного (по оси

х)

движения частицы. Для потенциально-

го барьера прямоугольной формы вы-

сотой

Uи

шириной /можем записать

При данных условиях задачи клас-

сическая частица, обладая энергией Е,

либо беспрепятственно пройдет над ба-

рьером (при Е > U), либо отразится от

него (при Е < U)

будет двигаться в

обратную сторону, т.е. она не может

проникнуть сквозь барьер. Для микро-

частицы, даже при Е > U, имеется от-

личная от нуля вероятность, что части-

ца отразится от барьера и будет двигать-

ся в обратную сторону. При Е <U име-

ется также отличная от нуля вероят-

ность, что частица окажется в области

х>

т.е. проникнет сквозь барьер. По-

добные, казалось бы, парадоксальные

выводы следуют непосредственно из

решения уравнения Шредингера, опи-

Рис.301

412

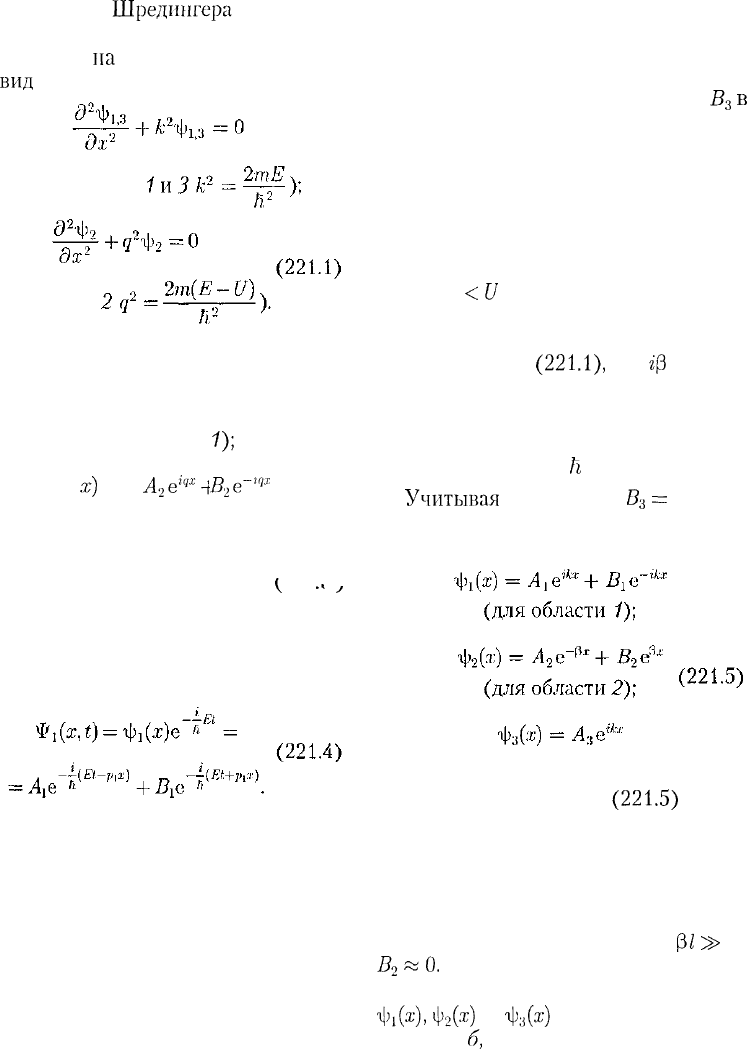
сывающего движение микрочастицы

при условиях данной задачи.

Уравнение

Шредингера

(217.5) для

стационарных состояний для каждой из

выделенных

на

рис. 301, а области име-

ет

вид

(для областей

(для области

Общие решения этих дифференци-

альных уравнений:

(221.2)

(для области

v);

я)

iqx

еГ

(для области 2);

(для области 3). ^ " '

В частности, для области 1 полная

волновая функция, согласно (217.4),

будет иметь вид

Решение (221.3) содержит также

волны (после умножения на временной

множитель), распространяющиеся в

обе стороны. Однако в области 3 име-

ется только волна, прошедшая сквозь

барьер и распространяющаяся слева

направо. Поэтому коэффициент

формуле (221.3) следует принять рав-

ным нулю.

В области 2 решение зависит от со-

отношений E>U или Е <U. Физичес-

кий интерес представляет случай, ког-

да полная энергия частицы меньше вы-

соты потенциального барьера, посколь-

ку при Е

законы классической фи-

зики однозначно не разрешают части-

це проникнуть сквозь барьер. В данном

случае, согласно

(221.1),

q =

ifi

— мни-

мое число, где

Учитывая

значение q и

0, полу-

чим решения уравнения Шредингера

для трех областей в следующем виде:

В этом выражении первое слагаемое

представляет собой плоскую волну

типа (219.3), распространяющуюся в

положительном направлении оси х (со-

ответствует частице, движущейся в сто-

рону барьера), а второе — волну, рас-

пространяющуюся в противоположном

направлении, т. е. отраженную от барь-

ера (соответствует частице, движущей-

ся от барьера налево).

(для области 3).

В области 2 функция

(221.5)

уже не

соответствует плоским волнам, распро-

страняющимся в обе стороны, посколь-

ку показатели степени экспонент не

мнимые, а действительные. Можно по-

казать, что для частного случая высо-

кого и широкого барьера, когда

(3/

^> 1,

^0.

Качественный характер функций

i^(x),

(ж)

г[)

(х)

иллюстрируется на

рис. 301,

б,

откуда следует, что волно-

413

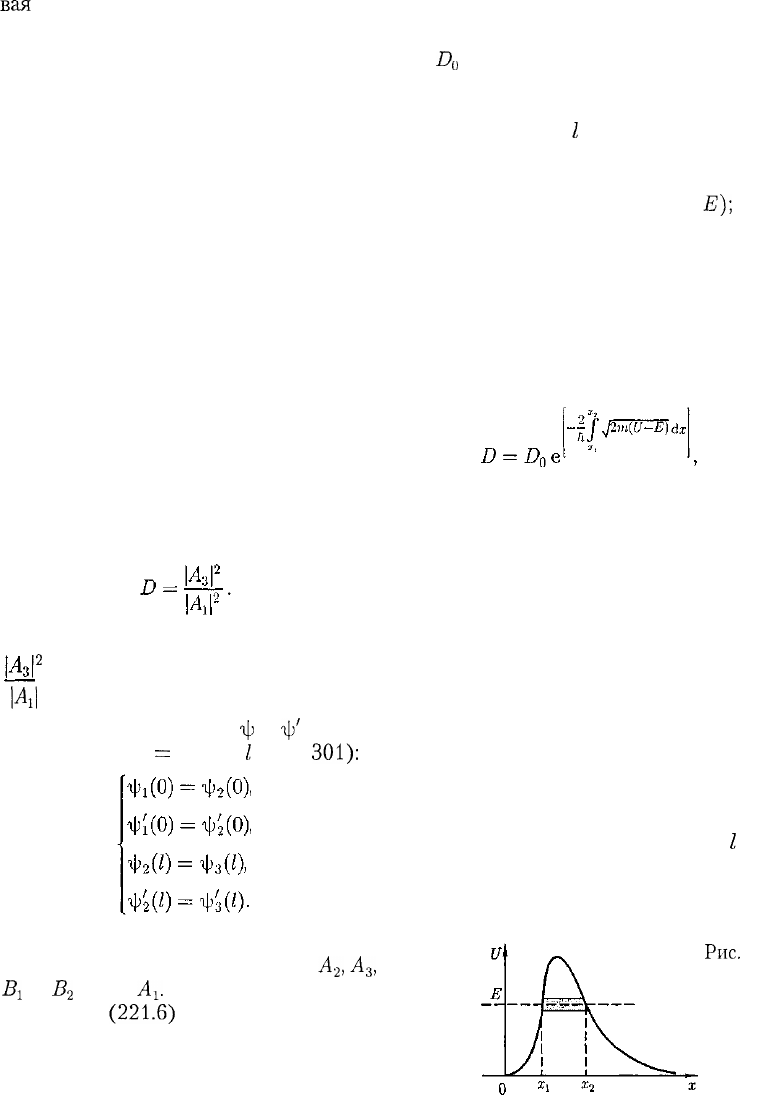
вая

функция не равна нулю и внутри ба-

рьера, а в области 3, если барьер не

очень широк, будет опять иметь вид

волн де Бройля с тем же импульсом, т. е.

с той же частотой, но с меньшей ампли-

тудой. Следовательно, получили, что

частица имеет отличную от нуля веро-

ятность прохождения сквозь потенци-

альный барьер конечной ширины.

Таким образом, квантовая механика

приводит к принципиально новому спе-

цифическому квантовому явлению, по-

лучившему название туннельного эф-

фекта, в результате которого микро-

объект может «пройти» сквозь потен-

циальный барьер.

Для описания туннельного эффек-

та используют понятие коэффициента

прозрачности D потенциального барье-

ра, определяемого как отношение плот-

ности потока прошедших частиц к

плотности потока падающих. Можно

показать, что

Для того чтобы найти отношение

, необходимо воспользоваться ус-

141

ловиями непрерывности

т|>

а{/

на гра-

ницах барьера х

0 и х =

(рис.

301):

(221.6)

Эти четыре условия дают возмож-

ность выразить коэффициенты

, А

через

Совместное решение

уравнений

(221.6)

для прямоугольного

потенциального барьера дает (в предпо-

ложении, что коэффициент прозрачно-

сти мал по сравнению с единицей)

(221.7)

где

Ц)

— постоянный множитель, кото-

рый можно приравнять единице; U —

высота потенциального барьера; Е —

энергия частицы;

— ширина барьера.

Из выражения (221.7) следует, что

D сильно зависит от массы т частицы,

ширины / барьера и от (U —

Е)\

чем

шире барьер, тем меньше вероятность

прохождения сквозь него частицы.

Для потенциального барьера произ-

вольной формы (рис. 302), удовлетво-

ряющей условиям так называемого ква-

зиклассического приближения (доста-

точно гладкая форма кривой), имеем

где U= U(x).

С классической точки зрения про-

хождение частицы сквозь потенциаль-

ный барьер при Е <U невозможно, так

как частица, находясь в области барье-

ра, должна была бы обладать отрица-

тельной кинетической энергией. Тун-

нельный эффект является специфиче-

ским квантовым эффектом.

Прохождение частицы сквозь об-

ласть, в которую, согласно законам клас-

сической механики, она не может про-

никнуть, можно пояснить соотношени-

ем неопределенностей. Неопределен-

ность импульса Ар на отрезке Ах =

со-

ставляет Ар > —. Связанная с этим раз-

бросом в значениях импульса кинети-

Рис.

302

414

ческая энергия

^—^—

может оказаться

2т

достаточной для того, чтобы полная

энергия частицы оказалась больше по-

тенциальной.

Основы теории туннельных перехо-

дов заложены в работах Л. И. Мандель-

штама

М.

А.

Леонтовича(

1903—1981).

Туннельное прохождение сквозь потен-

циальный барьер лежит в основе мно-

гих явлений физики твердого тела (на-

пример, явления в контактном слое на

границе двух полупроводников), атом-

ной и ядерной физики (например,

а-

распад, протекание термоядерных реак-

ций).

§ 222. Линейный гармонический

осциллятор

в квантовой механике

Линейный гармонический осцил-

лятор — система, совершающая одно-

мерное движение под действием квази-

упругой силы, — является моделью, ис-

пользуемой во многих задачах класси-

ческой и квантовой теории (см. § 142).

Пружинный, физический и математи-

ческий маятники — примеры класси-

ческих гармонических осцилляторов.

Потенциальная энергия гармони-

ческого осциллятора [см. (141.5)] равна

(222.1)

где

— собственная частота колебаний

осциллятора; т — масса частицы.

Зависимость (222.1) имеет вид пара-

болы (рис. 303), т.е. «потенциальная

яма» в данном случае является парабо-

лической.

Амплитуда малых колебаний клас-

сического осциллятора определяется

его полной энергией Е (см. рис. 17).

п=2

Рис.

303

В точках с координатами

±х

тах

полная

энергия Е равна потенциальной энер-

гии. Поэтому с классической точки зре-

ния частица не может выйти за преде-

лы области

(—х

1Х

,+х

хх

Такой выход

означал бы, что ее потенциальная энер-

гия больше полной, что абсурдно, так

как приводит к выводу, что кинетичес-

кая энергия отрицательна. Таким обра-

зом, классический осциллятор находит-

ся в «потенциальной яме» с координа-

тами

—х

тях

птх

«без права выхо-

да» из нее.

Гармонический осциллятор в кван-

товой механике — квантовый осцил-

лятор — описывается уравнением

Шре-

дингера

(217.5),

учитывающим выраже-

ние (222.1) для потенциальной энергии.

Тогда стационарные состояния кванто-

вого осциллятора определяются урав-

нением Шредингера вида

= 0, (222.2)

где Е — полная энергия осциллятора.

В теории дифференциальных урав-

нений доказывается, что уравнение

(222.2) решается только при собствен-

ных значениях энергии

(222.3)

Формула (222.3) показывает, что

энергия квантового осциллятора может

415

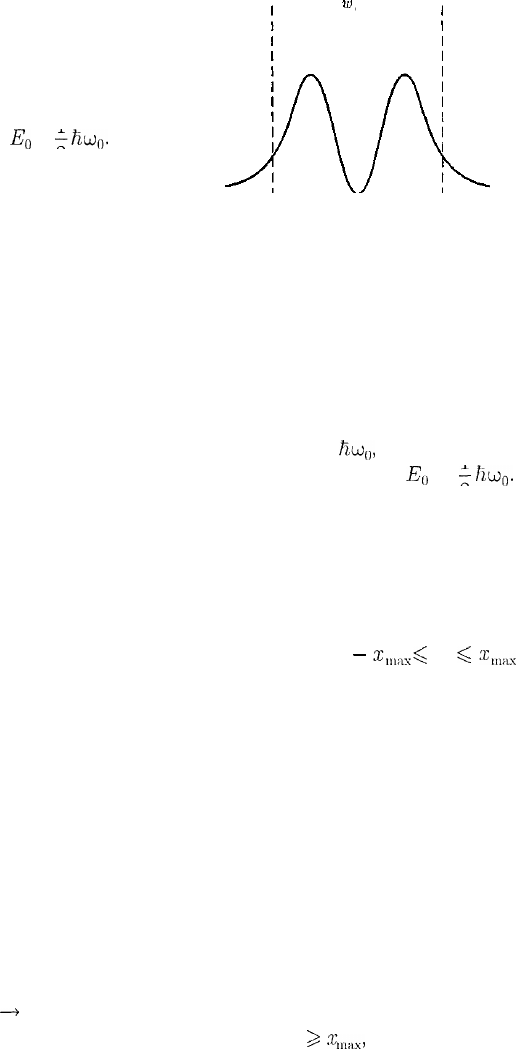
иметь лишь дискретные значения, т. е.

квантуется. Энергия ограничена сни-

зу отличным от нуля, как и для прямо-

угольной «ямы» с бесконечно высоки-

ми «стенками» (см. § 220), минималь-

ным

значением энергии

—HUQ.

Су-

ществование минимальной энергии —

она называется энергией нулевых ко-

лебаний — является типичной для кван-

товых систем и представляет собой пря-

мое следствие соотношения неопреде-

ленностей.

Наличие нулевых колебаний означа-

ет, что частица не может находиться на

дне «потенциальной ямы» (независимо

от формы ямы). В самом деле, «падение

на дно ямы» связано с обращением в

нуль импульса частицы, а вместе с тем и

его неопределенности. Тогда неопреде-

ленность координаты становится сколь

угодно большой, что противоречит, в

свою очередь, пребыванию частицы в

«потенциальной яме».

Вывод о наличии энергии нулевых

колебаний квантового осциллятора про-

тиворечит выводам классической тео-

рии, согласно которой наименьшая

энергия, которую может иметь осцил-

лятор, равна нулю (соответствует поко-

ящейся в положении равновесия части-

це). Например, согласно выводам клас-

сической физики при Т = 0 энергия

колебательного движения атомов кри-

сталла должна была бы обращаться в

нуль. Следовательно, должно исчезать

и рассеяние света, обусловленное коле-

баниями атомов. Однако эксперимент

показывает, что интенсивность рассея-

ния света при понижении температуры

не равна нулю, а стремится к некоторо-

му предельному значению, указываю-

щему на то, что при Т —> 0 колебания

атомов в кристалле не прекращаются.

Это является подтверждением наличия

нулевых колебаний.

Рис.

304

Из формулы (222.3) также следует,

что уровни энергии линейного гармо-

нического осциллятора расположены

на одинаковых расстояниях друг от

друга (см. рис. 303), а именно расстоя-

ние между соседними энергетическими

уровнями равно

/ГШ

причем минималь-

ное значение энергии

-Ны

Строгое решение задачи о квантовом

осцилляторе приводит еще к одному

значительному отличию от классическо-

го рассмотрения. Квантово-механиче-

ский расчет показывает, что частицу

можно обнаружить за пределами дозво-

ленной области —

ишх

^ х ^

1[тх

(см.

рис. 17), в то время как с классической

точки зрения она не может выйти за

пределы этой области.

Таким образом, имеется отличная от

нуля вероятность обнаружить частицу

в той области, которая является клас-

сически запрещенной. Этот результат

(без его вывода) демонстрируется на

рис. 304, где приводится квантовая

плотность вероятности w обнаружения

осциллятора для состояния п = 1. Из

рисунка следует, что для квантового ос-

циллятора действительно плотность ве-

роятности w имеет конечные значения

за пределами классически дозволенной

области \х\ ^

.т

1Х

т.е. имеется конеч-

ная (но небольшая) вероятность обна-

ружить частицу в области за предела-

416

ми «потенциальной ямы». Существова-

няется

возможностью прохождения

ние

отличных от нуля значений w за микрочастиц сквозь потенциальный ба-

пределами «потенциальной ямы» объяс-

рьер

(см. §

221).

Контрольные вопросы

• Чему равны фазовая и групповая скорости фотона?

-г,

Av,

• В каком случае и почему при УСЛОВИЯХ —-

<С

1 и —-

1 можно говорить о

движс-

г>,

нии частицы по определенной траектории?

• Как исходя из соотношения неопределенностей объяснить наличие

естественной

шири-

ны

спектральных

линий?

• Что определяет квадрат модуля волновой функции?

•

Почему

квантовая механика является статистической теорией?

• В чем отличие понимания причинности в классической и квантовой механике?

• Какова наименьшая энергия частицы в «потенциальной яме» с бесконечно высокими

«стенками»?

• Больше или меньше энергия частицы, находящейся в «потенциальной яме» с бесконеч-

но высокими «стенками», в состоянии п = 3 но сравнению с состоянием п = 1? Во сколь-

ко раз?

• Какими свойствами микрочастиц обусловлен туннельный эффект?

• В чем отличие поведения классической и квантовой частиц с энергией Е < U при их

движении

к прямоугольному потенциальному барьеру конечной ширины?

• Как изменится коэффициент прозрачности потенциального барьера с ростом его высо-

ты? с увеличением массы частицы? с увеличением полной энергии частицы?

• Как изменится коэффициент прозрачности потенциального барьера с увеличением его

ширины в два раза?

• Чему равна разность энергий между четвертым и вторым энергетическими уровнями

квантового осциллятора?

• Может ли частица находиться па дне «потенциальной ямы»? Определяется ли это фор-

мой «ямы»?

• Зависит ли распределение энергетических уровней от формы «потенциальной ямы»?

Ответ проиллюстрировать.

• В чем отличие

квантово-механического

и классического описания гармонического ос-

циллятора? В выводах этих описаний?

ЗАДАЧИ

28.1. Свободная частица движется со скоростью

и.

Докажите, что выполняется соотно-

шение

г)ф

а:)

= с

28.2. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что

допускаемая неопределенность скорости составляет 1 % от ее числового значения, опреде-

лите неопределенность координаты электрона. Применимо ли в данном случае для элект-

рона понятие траектории? [Ах = 33 им; нет]

28.3.

ф-Функция

некоторой частицы имеет вид

ч[>

= — е

где

г—

расстояние этой час-

тицы от силового центра, а — постоянная. Определите среднее расстояние

(г)

частицы от

силового

центра,

[(г)

Курс

физики

417

28.4. Запишите уравнение

Шредингера

для стационарных состояний электрона, нахо-

дящегося в атоме водорода.

28.5. Электрон находится в одномерной прямоугольной «потенциальной яме» шири-

ной /с бесконечно высокими «стенками». Определите вероятность

Wобнаружения

элект-

рона в средней трети «ямы», если электрон находится в возбужденном

состоянии

(п = 2).

Поясните физический смысл полученного

результата,

изобразив графически плотность

вероятности обнаружения электрона в данном состоянии.

[

0,195]

28.6. Прямоугольный потенциальный барьер имеет ширину 0,1 им.

Определите

в элект-

рон-вольтах разность энергий U — Е, при которой вероятность прохождения электрона

сквозь барьер составит 0,99. [0,1 мэВ]

Глава 29

ЭЛЕМЕНТЫ СОВРЕМЕННОЙ ФИЗИКИ

АТОМОВ И МОЛЕКУЛ

§ 223. Атом водорода

в квантовой механике

Решение задачи об энергетических

уровнях электрона для атома водорода

(а также

водородоподобных

систем:

иона гелия

Не

двукратно ионизован-

ного лития

и др.) сводится к зада-

че о движении электрона в

кулонов-

ском поле ядра.

Потенциальная энергия взаимодей-

ствия электрона с ядром, обладающим

зарядом Ze (для атома водорода Z

—

1),

(223.1)

где

— расстояние между электроном

и ядром.

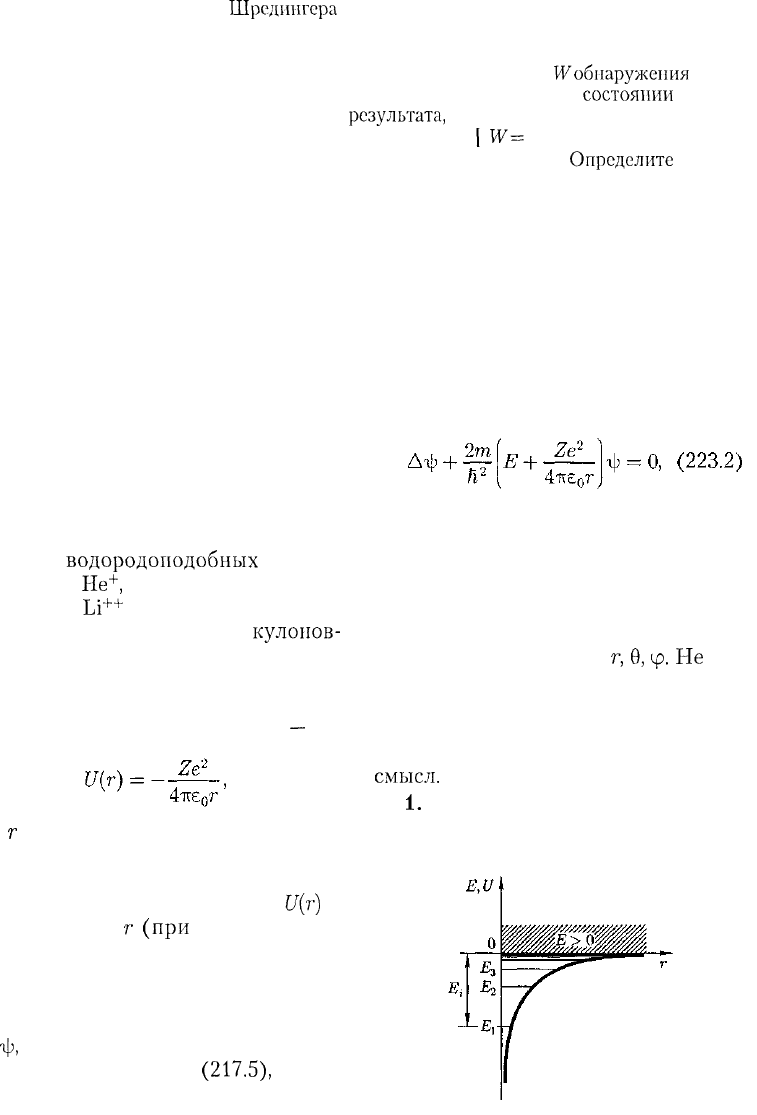
Графически функция U(r) изображе-

на жирной кривой на рис. 305.

U{r)

уменьшением

г(при

приближении

электрона к ядру) неограниченно убы-

вает.

Состояние электрона в атоме водо-

рода описывается волновой функци-

ей

а[),

удовлетворяющей стационарному

уравнению Шредингера

(217.5),

учиты-

вающему значение (223.1):

где т — масса электрона; Е — полная

энергия электрона в атоме.

Так как поле, в котором движется

электрон, является центрально-сим-

метричным, то для решения уравнения

(223.2) обычно используют сфериче-

скую систему координат:

г,

ip.

вда-

ваясь в математическое решение этой

задачи, ограничимся рассмотрением

важнейших результатов, которые из

него следуют, пояснив их физический

смысл.

Энергия. В теории дифференци-

альных уравнений доказывается, что

Рис.

305

418

уравнения типа (223.2) имеют решения,

удовлетворяющие требованиям одно-

значности, конечности и непрерывнос-

ти волновой функции

а[>,

только при

собственных значениях энергии

т.е. для дискретного набора отрица-

тельных значений энергии.

Таким образом, как и в случае «по-

тенциальной ямы» с бесконечно высо-

кими «стенками» (см. § 220) и гармо-

нического осциллятора (см. § 222), ре-

шение уравнения Шредингера для ато-

ма водорода приводит к появлению

дискретных энергетических уровней.

Возможные значения

E-

... по-

казаны на рис. 305 в виде горизонталь-

ных прямых.

Самый нижний уровень

{

отвеча-

ющий минимальной возможной энер-

гии, — основной, все остальные

(Е

п =

2,3,...)

— возбужденные (см. §

212).

При Е < 0 движение электрона явля-

ется связанным — он находится внут-

ри гиперболической «потенциальной

ямы». Из рисунка следует, что по мере

роста главного квантового числа п энер-

гетические уровни располагаются тес-

нее и при п = оо

Е^

= 0. При Е > 0 дви-

жение электрона является свободным;

область непрерывного спектра Е > 0

(заштрихована на рис. 305) соответ-

ствует ионизованному атому. Энергия

ионизации атома водорода равна

Выражение (223.3) совпадает с фор-

мулой (212.3), полученной Бором для

энергии атома водорода. Однако если

Бору пришлось вводить дополнитель-

ные гипотезы (постулаты), то в кванто-

вой механике

дискретные

значения

энергии, являясь следствием

самой

те-

ории, вытекают непосредственно из ре-

шения уравнения Шредингера.

2. Квантовые числа. В квантовой

механике доказывается, что уравнению

Шредингера (223.2) удовлетворяют

собственные функции

ijj,

n/m;

(г,

ф),

оп-

ределяемые тремя квантовыми числа-

ми: главным п, орбитальным

и магнит-

ным

1Щ.

Главное квантовое число п, соглас-

но (223.3), определяет энергетические

уровни электрона в атоме и может при-

нимать любые целочисленные значе-

ния, начиная с единицы:

Из решения уравнения Шредингера

вытекает, что момент импульса (меха-

нический орбитальный момент) элект-

рона квантуется,

т.

е. не может быть про-

извольным, а принимает дискретные

значения, определяемые по формуле

(223.4)

где

— орбитальное квантовое чис-

ло, которое при заданном п принимает

значения

1=0,1,

...,(п- 1), (223.5)

т.е. всего п значений, и определяет мо-

мент импульса электрона в атоме.

Из решения уравнений Шрединге-

ра следует также, что вектор

момента

импульса электрона может иметь лишь

такие ориентации в пространстве, при

которых его проекция

на направле-

ние z внешнего магнитного поля при-

нимает квантованные значения, крат-

ные

Yim

(223.6)

где

nil

~ магнитное квантовое число,

которое при заданном

может прини-

мать значения

0,±1,±2,

...,±1,

(223.7)

419

т.е. всего

+ 1 значений. Таким обра-

зом, магнитное квантовое число

т,

оп-

ределяет проекцию момента импульса

электрона на заданное направление,

причем вектор момента импульса элек-

трона в атоме может иметь в простран-

стве

+ 1

ориентации.

Наличие квантового числа т, долж-

но привести в магнитном поле к рас-

щеплению уровня с главным кванто-

вым числом п на

+ 1

подуровне!i.

Со-

ответственно в спектре атома должно

наблюдаться расщепление спектраль-

ных линий. Действительно, расщепле-

ние энергетических уровней в магнит-

ном поле было обнаружено в 1896 г.

голландским физиком

П.Зеемаиом

(1865— 1945) и получило название эф-

фекта

Зеемана.

Расщепление

уровней

энергии во внешнем электрическом

поле, тоже доказанное

эксперименталь-

но, называется эффектом

ШтаркаК

Хотя энергия электрона (223.3) и

зависит только от главного квантового

числа п, но каждому собственному зна-

чению

(кроме

Е{)

соответствует не-

сколько собственных функций

i|j,,

/m/

от-

личающихся значениями /и

гп,[.

Следо-

вательно, атом водорода может иметь

одно и то же значение энергии, находясь

в нескольких различных состояниях.

Так как при данном п орбитальное

квантовое число / может изменяться от

О до п — 1 [см. (223.5)], а каждому зна-

чению / соответствует 2/+ 1 различных

значений

(223.7), то число различ-

ных состояний, соответствующих дан-

ному п, равно

(223.8)

Квантовые числа и их значения яв-

ляются следствием решений уравнений

И. Штарк (1874 — 1957) —

немецкий

физик.

Шредингера

и условий однозначности,

непрерывности и конечности, налагае-

мых па волновую функцию

г|;.

Кроме

того, так как при движении электрона

в атоме существенны волновые свой-

ства электрона, то квантовая механика

вообще отказывается от классического

представления об электронных орби-

тах. Согласно

квантовой

механике, каж-

дому энергетическому состоянию соот-

ветствует волновая функция, квадрат

модуля которой определяет вероят-

ность обнаружения электрона в едини-

це объема.

Вероятность обнаружения электро-

на в различных частях атома неодина-

кова. Электрон при своем движении как

бы «размазан» по всему объему, обра-

зуя электронное облако, плотность (гу-

стота) которого характеризует вероят-

ность нахождения электрона в различ-

ных точках объема атома. Квантовые

числа п и

характеризуют размер

форму электронного облака, а

квагппо-

вое число

~ ориентацию электрон-

ного облака в пространстве.

В атомной физике,

по

аналогии со

спектроскопией, состояние электрона,

характеризующееся квантовыми числа-

ми

0, называют s-состоянием (элек-

трон в этом состоянии называют s-элек-

троном),

1—1

—

^-состоянием,

1=2

—

d-состоянием,

/ = 3 — /-состоянием и

т. д. Значение главного квантового чис-

ла указывается перед условным обозна-

чением орбитального квантового чис-

ла. Например, электроны в состояниях

с п

2 и /

0 и 1 обозначаются соответ-

ственно символами 2s

2р.

На рис. 306 для примера приведено

распределение электронной плотности

(формы электронного облака) для состо-

яний атома водорода при п= 1

п = 2,

определяемое

|oJ;

Как видно из ри-

сунка, оно зависит от п,

пц.

Так, при

0 электронная плотность отлична от

420