Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Tomography methods of recovering the image of medium 333

is the covariance matrix of the legitimate (with respect to the µ-th parameter ﬁeld)

signal;



6=µ

∗

+ K

εε



is the covariance matrix of the eﬀective noise that includes the statistical correlations

of the ﬁelds {ν

, µ

6= µ} as well as of the random component ε. The error variance

of the estimation ˆα is of the form

E(η

)

= hl|K

− K

∗



∗

6=µ

∗

+ K

εε



−1

|li,

or, in terms of the Fisher’s operator,

E(η

)

= hl|F

−1

|li,







∗





6=µ

+ K

εε





−1

+ K

−1







The latter expression clearly demonstrates that the higher the sensitivity of the

data processed to the variations of the µ-th ﬁeld and the less the inﬂuence of the

variations of the other ﬁelds (µ

6= µ) on the experimental data, the higher quality

of the estimation of the µ-th ﬁeld.

The model of experimental data (11.9) formally includes (Troyan, 1982) all the

ﬁelds of the parameters of the medium that occur in the propagation equation of

the sounding signal. Taking into account the observation system under a chosen

experimental design, we know a priori that the magnitude of the signal-to-noise ratio

is not necessarily large for all of the ﬁelds ν

(δθ). In order to construct an adequate

model of experimental data, it is necessary to introduce a quantitative measure

of the inﬂuence of the variations of each of the parameters on the measurement

ﬁeld. To this end, we introduce the notation of the information sensitivity of the

observation ﬁeld (u) with respect to a ﬁxed linear parameter ﬁeld (ν(δθ)) as the

limit of the derivative of the Shannon information I

(l(ν)/u) on α with respect to

α −→ 0 (signal-to-nose ratio), as α tends to zero:

= lim

α−→0

∂

∂α



l(ν)





l(ν)



E(η

apr

)

E(η

)

, E(η

apr

)

= hl|K

νν

|li,

E(η

)

= hl|(P

∗

−1

εε

P + K

−1

νν

)

−1

|li,

334 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

εε

= σ

I , K

νν

= σ

I , α = σ

/σ

The explicit expression for the derivative with respect to α is as follows:

∂

∂α



l(ν)



= −

hl|li

hl|I − αP

∗

(αP P

∗

+ I)

−1

P |li



−

hl|P

∗

(αP P

∗

+ I)

−1

P |li

hl|li

+ α

hl|P

∗

(αP P

∗

+ I)

−1

P P

∗

(αP P

∗

+ I)

−1

P |li

hl|li



By passing to the limit as α −→ 0, we obtain

= lim

α−→0



l(ν)



hl|P

∗

P |li

hl|li

||P |l > ||

|||l > ||

. (11.13)

The area of application of the information sensitivity includes the construction

of the model of experimental data and the design of tomographic experiment.

Physically, expression (11.13) means that the greater energy of the legitimate

signal that has passed through the medium with a nonhomogeneity, the ﬁeld of

which coincides with the weight function of the estimate functional l the higher the

information sensitivity of a given system of tomographic functionals. In the case of

the ray tomography, such a qualitative conclusion is obvious if the functional under

the estimation is of the type of mean over volume elements. An important property

of the measure of information sensitivity introduced above is that it provides a

quantitative characteristic for arbitrary tomographic functionals (we recall that the

functionals of the diﬀraction tomography are alternating Sec. 4.3) and arbitrary

functionals to be estimated (e.g. the coeﬃcients of the space Fourier transform of

the unknown parameter ﬁeld). This measure of the information sensitivity makes

it possible to determine the contribution of each of the ﬁelds involved in the model

(11.9) and to construct an adequate model, from which all ﬁelds not informationally

covered by a chosen design of the experiment (the set of tomographic functionals)

are excluded.

11.4 Errors of Recovery, Resolving Length and Backus and Gilbert

Method

To analyze the errors of recovering, we shall follow to the scheme from Sec. 9.3.

Neglecting the inﬂuence of all ﬁeld ν

, except one ﬁeld, we rewrite the representation

for the error of the estimate (11.11):

= hl − (α, p)νi − (α, ε) (11.14)

then, introducing the notation b (displacement) and e (noise):

η = b + e,

Tomography methods of recovering the image of medium 335

where b = E

η = hl − (α, p)νi ≡ hl −

l|νi; e = −(α, ε); E

denotes the conditional

mathematical expectation.

We should note, that the general reason for an ill-posed statement of the esti-

mation problem consists in an absence of a priori information about the solution

set {ν(δθ)} (Backus and Gilbert, 1967, 1968). Actually, an unbiased estimate can

be obtained if estimated functional l belongs to the linear span of the tomographic

functionals (α, p). But the latter condition a fortiori not holds, if, for example, l is

singular, but p

are regular (n = 1 ÷ N). So, the error of the estimate η

in the

general case can be inﬁnite by the virtue of the unboundness of the set {ν(δθ)}.

Therefore it is impossible to introduce any optimal criterion for the estimation.

Taking into account the mentioned above problem, we will analyze the Backus

and Gilbert method (B – G) (Sec. 6.16), which is wide represented in scientiﬁc liter-

ature (Jensen et al., 2000; Troyan, 1985; Yanovskaya and Porokhova, 2004; Nolet,

1985). Let us brieﬂy explain the idea and the algorithmic structure of (Backus

and Gilbert, 1968), in which a presence of the random component in a measure-

ment data is assumed, but a priori information about the set of solutions {ν(δθ)}

is supposed to be absent. Using the notations of the formula (11.14), we write

the optimality criterion in a sense of Backus and Gilbert criterion. In the work

(Ryzhikov and Troyan, 1987) a one-dimensional problem (x ∈ R

) is considered.

The criterion J

B−G

contains two components. The ﬁrst one (R-criterion “delta-

likeness”): a singular functional h

B−G

| = δ(x − X) is estimated. If we denote

(α, p) ≡ (α(X), p(x)) ≡

l, then

R = hl

B−G

−

l|K

B−G

−

li,

where the integral operator K

B−G

has a singular kernel of the form

B−G

, x

) = c(x

− X)(x

− X)δ(x

− x

which contains the estimated point X. We write the value of R relatively to α

parameter

R = (α, V

∗

α),

where

∗

= c

)(x

− X)δ(x

− x

)(x

− X)p

)

= c

(x)p

(x)(x − X)

dx.

The value of R is connected with the resolution of the method on x coordinate; for

this purpose the constant c in R

is assumed to be 12, because, if we put to criterion

R = 12

l(x)(x − X)

an uniform at the interval ∆ distribution, instead of the linear combination

l =

n=1

(X)p

(x),

336 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

(which produce “solving kernel”), then R will be numerically equal to a value of

the interval ∆, i.e.

R = 12

(x)(x − X)

dx ← 12

X+∆/2

X−∆/2



∆

(x − X)



dx ≡ ∆.

Here ∆ is the resolving length on the coordinate x.

An inﬂuence of the random component ε, cased, for example, by measurement

errors, is taken into account by the second component of the J

B−G

criterion:

N(α, K

α)

= E(εε

) is a covariance matrix of the measurement errors).

Finally, the optimality criterion for the estimation of the functional l consists in

minimizing on α the sum of the weighted quadratic forms R and N:

B−G

= (1 − γ)R + γN, γ ∈ [0, 1],

B−G

= (1 − γ)hl −

l|K

B−G

|l −

li + γ(α, K

α)

under the condition h

l|1i = 1. The supplementary condition is introduced by anal-

ogy with hl

B−G

|1i ≡

δ(x − X)dx. It is possible to see, that without the supple-

mentary condition the criterion produces only an unique zero solution.

It is assumed to minimize the criterion J

B−G

under various values of the pa-

rameter γ, and the optimality estimate (ˆα) corresponds to the minimum or the

sum R and N, that provides under ideology of the Backus and Gilbert method a

compromise between “resolving length” and “error”.

We shall compare the optimality criterion J

B−G

and optimality criterion in-

troduced by Ryzhikov and Troyan (R–T) (Ryzhikov and Troyan, 1994), which is

considered in Sec. 11.3:

P−T

= [(Λ − Q

∗

α)

∗

P−T

(Λ − Q

∗

)].

This criterion for the considered case of the single one-dimensional estimated ﬁeld

without any a priori link between ν(δθ) and ε) we write down in the form

P−T

= hl

P−T

−

l|K

νν

P−T

−

li + (α, K

α).

It was mentioned, the ﬁrst term of J

P−T

criterion, which is connected with the

displacement b, must include a priori information about ν(δθ). In the criterion J

P−T

this a priori information is introduced by the operator K

P−T

, which determines a

set of feasible solutions {ν(δθ)}. A priori information can be introduced in the

probability form, for example, by determination of the Gaussian measure on the set

{ν(δθ)}. In this case the operator K

P−T

makes a sense of the a priori covariance

operator of the ﬁeld {ν(δθ)}.

Tomography methods of recovering the image of medium 337

The class of the solution ν(δθ) can be determined also by inequality hν|H|νi ≤ C,

where H is the Hermitian positive operator. For example, in the case of

x ∈ R

, H =

q=0

∂

(u∂

), u < 0,

then with accurate within a factor γ, which is a regularization parameter, the oper-

ator K

P−T

is the Green operator for the operator H, in addition the class {ν(δθ)}

is interpreted as a class of solutions of the r-th degree of smoothness.

The ﬁrst component of the criterion J

B−G

is a quadratic form of the displace-

ment. The integral operator K

B−G

with a singular kernel brings a priori information

about the solution set. This operator implicitly depends on the point X, which loca-

tion is not determined. So, a priori information in the Backus and Gilbert method is

transformed together with a change of the point X, that is inadmissible in the pro-

cessing of the ﬁxed volume of experimental data. The solving kernel (α(X), p(x)) is

oscillating one and the interpretation of the ﬁrst component of J

B−G

as a resolving

length is incorrect. Probably it is better instead of the functional l

= δ(x −X) to

use the functional which has a sense of a middle value of a desired ﬁeld ν(δθ) in the

vicinity of the point X. In this case a diameter of the vicinity is determined “re-

solving length”, and the error of the estimate has a variance hl|F |li, which includes

the displacement b and the noise e.

The linear constraint h

l|1i, which is used in J

B−G

, is an artiﬁcial one. Its

appearance is caused by two reasons: ﬁrst, the estimated functional is localized in

the point X; second, the kernel K

B−G

is equal to zero in the same point. So, without

the linear constraint we can not obtain the proper estimate. It should underscore,

that the delta function is not deﬁned by the condition hl

|1i = 1, it is deﬁned by

the condition hl

|ψi = ψ(X) The logic of the Backus and Gilbert method leads to

the necessity to introduce an inﬁnite number of the (delta-like) linear constraints

l|ψ

i = ψ(X) (where {ψ

} is a complete system of the basis functions).

If the kernel k

B−G

does not equal to zero in the point X, then the optimality

criterion does not need the linear constraints The various shapes of the kernel k

B−G

are considered in (Backus and Gilbert, 1968), but most of the applications use the

kernel of the form

B−G

= c(x

− X)(x

− X)δ(x

− x

One can show, that the introducing of the linear constraint in (R–T)-algorithm

leads to increasing of the estimate variance. In this case (R–T)-criterion has a form

P−T

= J

P−T

+ γhl −

l|ν

(ν

is a model ﬁeld) and an optimal estimate

˜α = arg inf

P−T

is determined as

˜α = K

−1

+ κu

338 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

where u

= P K

νν

|li; u

= P ν

; K

= P K

νν

∗

+ K

;

κ =

|ν

i − u

−1

Using the expression for κ, we, ﬁnally, obtain

˜α =



I −

−1



−1

+ hl

|ν

−1

Let write an increasing of the variance of the estimate of the functional l

after

introducing of the linear constraint to the criterion

∆η

= (˜η − η)

(hl

|ν

i − u

−1

)

−1

≥ 0.

Analysis of the ∆η

shows, that introducing of the supplementary linear constraint

−

l|ν

i = 0 (like to usage of h

l|1i = 1 in the Backus and Gilbert criterion), leads

to loss of the estimation eﬃciency.

After carrying out the analysis we can conclude, that the correct restoration

algorithm for the parameters using seismic data should be based on the quadratic

optimality criterion:

P−T

= hl

P−T

−

l|K

P−T

−

li,

where as the estimated functional l

P−T

we use the mean value of the desired ﬁeld

in the vicinity of the point X; for example, in a rectangular parallelepiped abc with

center in the point (X

, X

P−T

= (abc)

−1



− |x

− X





− |x

− X





− |x

− X



H(ξ) =



1, if ξ ≥ 0,

0, if ξ < 0.

The variance of the estimate reads as

Eη

= hl

P−T

−1

P−T

and it includes both the displacement b and noise e.

The criterion J

P−T

in the full measure takes into account both a priori infor-

mation about the elastic ﬁeld and statistical structure of observation errors. In

Fig. 11.1 the integral kernels for the operators of the criterion K

B−G

(a),

B−G

, x

) = (x

− X)(x

− X)δ(x

− x

are represented: K

P−T

for the noncorrelated homogeneous ﬁeld(b) and K

P−T

for

the Markovian homogeneous ﬁeld (c), which determine an introducing a priori in-

formation in (B–G) and (P–T) methods.

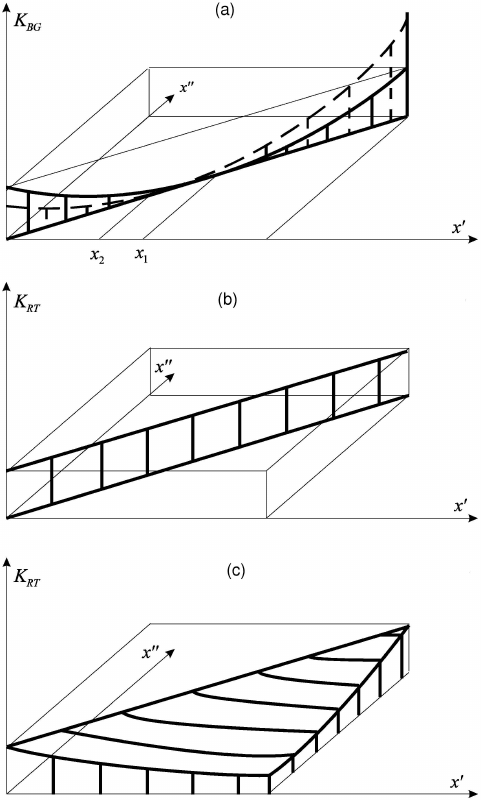
Tomography methods of recovering the image of medium 339

Fig. 11.1 Integral kernels of the correlation operators: (a) corresponds to ( B–G)-method, (b)

and (c) correspond to (P–T)-method for the noncorrelated homogeneous ﬁeld and the Markovian

homogeneous ﬁeld respectively.

340 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

11.5 Back Projection in Diﬀraction Tomography

Let us remind the model for the diﬀraction tomography experiment:

u = P θ + ε,

where the tomographic operator P is

P θ ⇒

(ξ, x)θ(x)dx,

(ξ, x) = hG

∗

[x]

i ≡ hϕ

out{t}

[x]

|ϕ

where G

∗

includes the time inversion under the interpretation of the nonstation-

ary sounding signal; the integral kernel of the tomography functional p(·, x) is the

weight function connected with the variation of the medium parameters in the space

point x and in the temporary point t. This weight function corresponds to the ξ

source-receiver pair and it produces by local interaction S

[x]

of the inverted ﬁeld

out{t}

∗

out

= h

, which is produced by the source h

located in the point ξ

and working in the inverse time t, and the incident ﬁeld ϕ

= s

The inversion of the data u using the regularized algorithm

θ = Ru is con-

structed on the basis of the solution of an extremum problem:

R = arg inf(kRP − Ik

+ kRk

where kAk

= (spABA

∗

)

1/2

reads as

R = K

∗

(P K

∗

+ K

)

−1

, (11.15)

and provides a minimum variance of the restoration error, i.e.

R = arg inf

spK

δθ

= K

− RK

∗

, K

= P K

∗

+ K

The construction of the optimum operator

R leads to some problems. The anal-

ogous problems appear at the realization of the exact algorithms in the conventional

ray tomography. But in the computational tomography these problems are solved

in the way of the construction of heuristic algorithms, which provide to use with

more or less eﬀectiveness some part of the information contained in the experimental

data. One of the routine methods of a such kind is the back projection procedure

(Vasilenko and Taratorin, 1986; Kireitov and Pikalov, 1985; Beylkin, 1985). We

should note that the back projection is a part of the exact analytical inversion of

the Radon transform (Helgason, 1999; Herman, 1980), which as a data for the back

projection are used the derivatives of the Hilbert images of the Radon projections.

Let us consider a suboptimal algorithm

R of the restoration with the use of the

inversion of the measured wave ﬁelds and the back projection. To write down the

algorithm

R in a form

θ(x) =

Ru(x) = α

−1

hΦ

out

[x]

|Φ

Tomography methods of recovering the image of medium 341

where the summation is implemented on the results of processing of the isolated

experiments; Φ

is a direct continuation of the wave ﬁeld, which produces by the

s-th set of the sources; Φ

out

is a backward continuation, measured by the r-th

set of receivers; α is a dimension factor, which is proportional to a volume of the

processed experimental data. After the parametrization of the experimental record

in the form

(t)

δ(t − t

)δ(x

− ξ

)δ(x

− ξ

we rewrite the expression for the estimate

θ(x):

θ(x) = α

−1

≡ α

−1

(ξ, x) = α

−1

∗

u. (11.16)

In this case the kernel of the tomography functional p

(ξ, x) is produced by the

hardware function of the recording channel h

= δ(t − t

)δ(x

− ξ

), that cor-

responds to a wide band recording of the experimental data. Let note, that the

last expression for the estimate

θ(x) contains the back projection procedure in the

explicit form.

We consider the back projection as a part of the generalized inversion algorithm

described in Sec. 11.3. For this purpose we write down the result of the restoration

of an arbitrary linear functional l(θ) ≡ hl|θi (Ryzhikov and Troyan, 1990):

l(θ) = h

l|θi = hu(P K

∗

+ K

)

−1

P K

|li

and consider its simpliﬁed version for K

⇒ I, hl| ⇒ hl

[x]

| ≡

≡ hδ(x − [x])|. Then the expression for

l(θ) reads as

[x]

≡ h

[

[x]

|θi = hu|(P P

∗

+ K

)

−1

P |l

[x]

Taking into account, that

P |l

[x]

i ⇒

(ξ, x)δ(x − [x])dx = P

(ξ, [x]),

and assuming (P P

∗

+ K

) ∼ αI, we obtain an analog of an action of the algorithm

[x]

∼ α

−1

(ξ, [x]).

The comparison of the formulas (11.15) and (11.16) allows us to see the disad-

vantages of the generalized inversion (or generalized back projection): it does not

taking into account a statistics of the measurement errors, a priori representations

about medium parameters are absent, the links between various generalized Radon

projections are ignored.

342 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

The certain advantage of the back projection consists in its manufacturing, be-

cause the algorithm is reduced to the well known procedures of the wave ﬁeld

continuation (Zhdanov et al., 1988; Claerbout, 1985; Kozlov, 1986; Petrashen and

Nakhamkin, 1973; Berkhout, 1984.; Stolt and Weglein, 1985).

Let us remind that classical methods of the elastic wave ﬁelds continuation

(Claerbout, 1976; Petrashen and Nakhamkin, 1973; Timoshin, 1978; Berkhout,

1985) reduce to the procedure ˜u = G

∗

u. As it follows from the analysis of the

generalized back projection algorithm (11.16), the procedure of the back continua-

tion is one of the component of the procedure of restoration of the image of medium:

out

= G

∗

u. From the representation (11.15) it follows, that an application of the

continuation as the method of the restoration needs an information about proper-

ties of the sounding signal Φ

and the information about the interaction character

of the direct and back continuation of the wave ﬁelds (S

). The algorithm of gen-

eralized back projection is virtual to the back continuation under conditions that

the incident ﬁeld Φ

has a plane wave-front and the interaction operator S

is a

multiplication operator.

Let note, that the procedure of the generalized back projection can be inter-

preted as a hologram processing. We would remind that the optical holography is

found on the registration both the amplitude and the phase of an optic signal at the

same time. In optics it implements by recording an interference picture, which ap-

pears as a result of the superposition between the monochromatic (laser) reference

beam and the wave ﬁeld scattered by the object. In the optic holography using a

monochromatic beam is a single opportunity to ﬁx both the amplitude and phase,

but in many sounding tasks recording ﬁelds contain both these parameters of the

scattering ﬁeld. The analogy with the holography is found in the explicit form in

the generalized back projection procedure:

θ ∼ α

−1

∗

(u − u

)|S

|ϕ

= ϕ



x=ξ

In this case the arbitrary ﬁeld ϕ

can be considered as the reference beam, but

as in the case of the optical holography, if it does not bring any information. The

“holography” image appears as the result of the interaction of the reference ﬁeld

and an illuminated “hologram” u − u

, at that an information transmission to

the space satisﬁes the same laws as the reference ﬁeld ϕ

. The interaction operator

is no multiplication operator in general case, and it determines only by the

propagation law for the sounding signal.

Let us show that the procedure of the construction of the ﬁeld ϕ

out

in the form

∗

u can be represented in the explicit form as an analytical extension of the ﬁeld

observed on some part of the space surface. Let us consider an example of the

extension of the scalar wave ﬁeld.

Using the second Green theorem in the form

[ϕ∇

ψ − ψ∇

ϕ]dV =

∂V

[ϕ

∇

∇ψ − ψ∇∇ϕ] · dσσ,