Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.

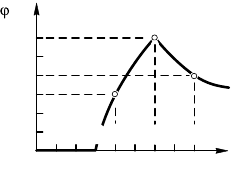
570
В области R
1
m r < R
2
потенциал поля внутренней сферы будет
изменяться по заону (2), а внешней — по заону (1):
ϕ (R
1
m r < R
2
) = + . (4)
В области r l R
2
потенциалы полей обеих сфер будут изменять-
ся по заону (2):
ϕ (r l R
2
) = + + . (5)
На раницах областей (при r = R
1
и r = R
2
) значение потенциала
можно найти по формулам (4), (5) при r = R
1
и r = R
2
соответственно:
ϕ (r = R
1
) = + = 0,
ϕ (r = R
2
) = d 600 В.
Точи 1, 2 и 3 лежат в областях 0 m r < R
1
, R
1
m r < R
2
, r l R
2
соответственно. Поэтому для точи, удаленной от центра сфер на
расстояние l
1
, из формулы (3) получим
ϕ (r = l
1
) = + = 0.
В точе, соответствующей расстоянию l
2
от центра сфер, потен-
циал найдем по формуле (4), положив r = l
2
:
ϕ (r = l
2
) = + d 300 В.
Наонец, в точе на расстоянии l
3
от центра сфер, потенциал
определим по формуле (5) при r = l
3
:
ϕ (r = l
3
) = d 450 В.
Графи зависимости ϕ(r) пред-
ставлен на рис. 10.7.9.
О т в е т: ϕ(r = l
1
) = 0; ϕ(r = l
2
) d
d 300 B; ϕ(r = l
3
) d 450 В;
рис. 10.7.9.
10.8.9. Если поверхность за-
землена, то ее потенциал равен
нулю. При сообщении средней
сфере заряда q на внутренней и
внешней сферах появятся заряды
q
1
и q
3
соответственно.
q
1
4πε
0
r
--------------- -
q
2
4πε
0
R
2
--------------------
q
1
4πε
0
r
--------------- -
q
2
4πε
0
r
--------------- -
q
1
q
2
+
4πε
0
r
----------------- -
q
1
4πε
0
R
1
--------------------
q
2
4πε
0
R
2
--------------------
q
1
q
2
+
4πε
0
R
2
--------------------
q
1
4πε
0
R
1
--------------------
q
2
4πε
0
R
2
--------------------
q
1
4πε
0
l
2
----------------- -
q
2
4πε
0
R
2
--------------------
q
1
q
2
+
4πε
0
l
3
----------------- -
, Â
0
10
300
400
600
15520253530 40
r
, ñì
l
1
l
3
R
1
l
2
R
2
Рис. 10.7.9

571
Сфера радиусом R заземлена, и ее потенциал
ϕ
1
= + + = 0; (1)
cфера радиусом R
3
заземлена, и ее потенциал
ϕ
3
= + + = 0, (2)
де k — элетричесая постоянная.
Из уравнений (1), (2) следует, что
4q
1
+ 2q + q
3
= 0, (3)
q
1
+ q + q
3
= 0. (4)
Решив систему уравнений (3), (4), получим
q
1
= – , q
2
= – q.
Найдем теперь зависимость ϕ(r) во всех областях пространства:
1) 0 m r m R, ϕ = + + = 0;
2) R m r m 2R, ϕ = + + = – ;
3) 2R m r m 4R, ϕ = + + = – ;
4) r l 4R, ϕ = + + = 0.
10.8.10. Несомпенсированные заряды моут располааться
тольо на поверхности проводниа.
Поверхностные плотности зарядов на внешних и внутренних
поверхностях плит равны , , , соответственно
(рис. 10.8.7, а). Заменим плиты четырьмя бесонечными проводя-
щими заряженными пластинами (рис. 10.8.7, б).
Пусть для определенности заряды на пластинах 1′′ и 2′ положи-
тельны, а на пластинах 1′ и 2′′ отрицательны.
Напряженности элетричесоо поля в точах 1 и 2 равны ну-
лю, и поэтому можем записать:
E
1
= + + – = = 0,
E
2
= + + – = = 0.
kq
1
R
---------
kq
2R
--------
kq
3
4R
---------
kq
1
4R
3
-----------
kq
4R
--------
kq
3
4R
---------
q
3
---
2
3
---
kq
1
R
---------
kq
2R
--------
kq
3
4R
---------
kq
1
r
---------
kq
2R
--------
kq
3
4R
---------
kq
3
------
⎝
⎛
1
R
----
1
r
---
⎠
⎞
kq
1
r
---------
kq
r
------
kq
3
4R
---------
kq
3
------
⎝
⎛
2
r
---
1
2R
--------
⎠
⎞
kq
1
r
---------
kq
r
------
kq
3
r
---------
σ
1
′
σ
1
′′
σ
2
′
σ
2
′′
E
2
′
E
1
′
E
1
′′
E
2
′′
σ
2
′
σ
1
′
σ
1
′′
σ
2
′′
−++
2ε
0
---------------------------------------------
E
2
′
E
2
′′
E
1
′
E
1
′′
σ
2
′
σ
2
′′
σ
1
′
σ
1
′′
−++
2ε
0
---------------------------------------------
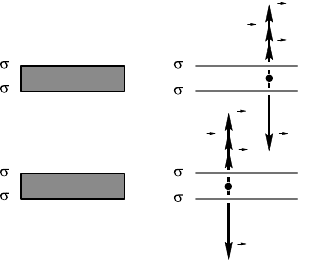
572
Решив эти уравнения, получим
= – , (1)
= . (2)
Заон сохранения заряда для аждой из плит (см. рис. 10.8.7, а):
σ
1
= + , (3)
σ
2
= + . (4)
Решив систему уравнений (1)—(4), получим о т в е т:
= – = , = = .
10.9.1. Сила взаимодействия между точечным зарядом и боль-
шой заземленной металличесой пластиной равна силе взаимодей-
ствия двух точечных зарядов q и (–q), расположенных зерально
относительно пластины. Следовательно,
F = = d 2,5 · 10
–4
Н,
де k = 9
.
10
9
м/Ф.
О т в е т: F d 2,5 · 10
–4
H.
10.12.6. В плосом онденсаторе одна пластина действует на
друую с силой
F = qE,
E
1
′
E
1
′′
E
2
′
E
2
′′
1
2
E
1
′
E
1
′′
E
2
′
E
2
′′
1
′
1
′′
2
′
2
′′
1′
2′
1′′
2′′
á)
1
′
1
′′
2
′
2
′′
1′
2′
1′′
2′′
à)
Рис. 10.8.7
σ
2
′
σ
1
′
σ
1
′′
σ
2
′′
σ
1
′
σ
1
′′
σ
2
′
σ
2
′′
σ
1
′
σ
2
′
σ
1
σ
2
−
2
------------------ -
σ
1
′′
σ
2
′′
σ
1
σ
2
+
2
------------------ -
kq
2
2l()
2
-------------
kq
2
4l
2
---------
573
де q — заряд одной пластины: q = C∆ϕ = ∆ϕ; E — напряжен-
ность поля друой пластины: E = = .
Решив систему приведенных уравнений, получим о т в е т:
F = d 4,4 · 10
–2
Н.
10.12.8. 1. Если онденсатор заряжен и отлючен от источни-
а, то заряд на ео обладах изменяться не будет. Поэтому энер-
ия онденсатора
W = .
Энерия онденсатора емостью C с диэлетриом была равна
W
1
= ;
после тоо а диэлетри вынули, энерия онденсатора стала
равна
W
2
= .
де C
′
= — емость онденсатора без диэлетриа. Следовательно,
= ε,
т. е. энерия онденсатора возросла в ε раз.
2. Если онденсатор подлючен источниу (разность потен-
циалов ∆ϕ между обладами постоянна), то ео энерия была
равна
W
1
= ;
после тоо а диэлетри вынули, энерия онденсатора стала
равна
W
2
= .
ε
0
S
d
---------
σ
2ε
0
-------- -
q
2ε
0
S
-------------
ε
0
S∆ϕ
2
2d
2
---------------------
q
2
2C
-------
q
2
2C
-------
q
2
2C
′
---------
C
ε
---
W
2
W
1
---------
C∆ϕ
2
2
---------------
C
′
∆ϕ
2
2
--------------- -
574
Следовательно,
= ,
т. е. энерия онденсатора уменьшилась в ε раз.
О т в е т: в первом случае энерия онденсатора увеличится в ε раз,
во втором — уменьшится в ε раз.
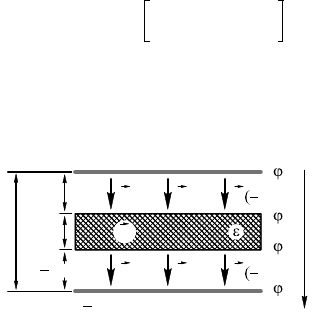
10.12.18. Поместим на облади онденсатора равные по
модулю разноименные заряды ±q, а поазано на рис. 10.12.6. На-
личие на обладах этих зарядов приведет появлению в воздуш-
ном зазоре элетричесоо поля напряженностью
E = E(q) + E(–q) = + = .
Внутри диэлетриа проницаемостью ε поле E будет ослаблено
в ε раз:
E′ = = .
Поля между обладами можно считать однородными, поэтому
разность потенциалов
∆ϕ = ϕ
1
– ϕ
2
= (ϕ
1
– ϕ
3
) + (ϕ
3
– ϕ
4
) + (ϕ
4
– ϕ
2
),
де ϕ
1
– ϕ
3
= Ex, ϕ
3
– ϕ
4
= E′a, ϕ
4
– ϕ
2
= E [d – (a + x)]. Следовательно,
∆ϕ = Ex + a + E [d – (a + x)] = E = [ε(d – a) + a].
Находим емость онденсатора:
C = = .
W
2
W
1
---------
1
ε
---
1
2
3
4
E q)
E
q)
Eq(
)
Eq(
)
E
E
x
da
q
q
d
(a + x)
E′
O
X
Рис. 10.12.6
q
2Sε
0
-------------
q
2Sε
0
-------------
q
Sε
0
---------
E
ε
----
q
Sεε
0
-------------
E
ε
----
ε xda− x−+()a+
ε
--------------------------------------------------
q
Sεε
0
-------------
q
∆ϕ
-------
εε
0
S
ε da−()a+
-------------------------------

575
10.13.6. Емость онденсатора C = . Конденсаторы C
1
и C
2
имеют заряды
q
1
= C
1
∆ϕ
1
и q
2
= C
2
∆ϕ
2
.
После соединения онденсаторов обладами, имеющими одно-
именные заряды, общий заряд батареи онденсаторов (случай а)
q = q
1
+ q
2
= C
1
∆ϕ
1
+ C
2
∆ϕ
2
,
а емость
C
общ
= C
1
+ C
2
.
Следовательно, разность потенциалов между точами a и b
∆ϕ = = ,
отуда получим
C
1
= = 4 мФ.
Если заряженные онденсаторы соединить обладами, имею-
щими разноименные заряды, то заряд батареи (случай б)
q = |q
1
– q
2
| = |C
1
∆ϕ
1
– C
2
∆ϕ
2
|.
Поэтому
∆ϕ = = ,
отуда получим
C
1
= = 36 мФ.
Ответ: а) С
1
= 4 мФ; б) С
1
= 36 мФ.
10.13.7. Пусть q
1
= C
1
U
1
и q
2
= C
2
U
2
— заряды на онденсато-
рах при разомнутом люче K, a и — заряды на онденсато-
рах после замыания люча. Начальная энерия заряженных он-
денсаторов
W
0
= + ,
q
∆ϕ
-------
q
C
общ
------------
C
1
∆ϕ
1
C
2
∆ϕ
2
+
C
1
C
2
+
------------------------------------------
C
2
∆ϕ ∆ϕ
2
−()
∆ϕ
1
∆ϕ−
------------------------------------
q
C
общ
------------
C
1
∆ϕ
1
C
2
∆ϕ
2
−
C
1
C
2
+
--------------------------------------------
C
2
∆ϕ ∆ϕ
2
+()
∆ϕ
1
∆ϕ−
------------------------------------
q
1
′
q
2
′
C
1
U
1
2
2
--------------
C
2
U
2
2
2
--------------
576
а онечная
W = + .
После замыания люча заряды перераспределяются таим об-
разом, что напряжения на онденсаторах станут одинаовы, т. е.
= . По заону сохранения заряда
+ = q
1
+ q
2
= C
1
U
1
+ C
2
U
2
.
Решив систему двух последних уравнений, находим
= и = .
Уменьшение потенциальной энерии системы онденсаторов
равно оличеству теплоты, выделившемуся на резисторе R:
Q = W
0
– W = + – – =
= + – – =
= = 3 · 10
–2
Дж.
О т в е т: Q = 3 · 10
–2
Дж.
10.13.15. Пусть С
0
— емость данной систе-
мы онденсаторов. Посольу система онденса-
торов бесонечно длинная, то, отделив от нее пер-
вое звено, мы получим систему, емость оторой
равна начальной (рис. 10.13.22). Емость таой
системы можно найти из соотношения:
= + + .
Отсюда получим о т в е т:
C
0
= .
10.13.18. Для определения разности потенциалов между точ-
ами A и B, равной
U
A–B
= ϕ
A
– ϕ
B
,
q
1
′
()
2
2C
1
--------------
q
2
′
()
2
2C
2
--------------
q
1
′
C
1
------
q
2
′
C
2
------
q
1
′
q
2
′
q
1
′
C
1
U
1
C
2
U
2
+()C
1
C
1
C
2
+
----------------------------------------------- -
q
2
′
C
1
U
1
C
2
U
2
+()C
2
C
1
C
2
+
----------------------------------------------- -
C
1
U
1
2
2
--------------
C
2
U
2
2
2
--------------
q
1
′
()
2
2C
1
--------------
q
2
′
()
2
2C
2
--------------
C
1
U
1
2
2
--------------
C
2
U
2
2
2
--------------
C
1
U
1
C
2
U
2
+()
2
C
1
2 C
1
C
2
+()
2
---------------------------------------------------
C
1
U
1
C
2
U
2
+()
2
C
2
2 C
1
C
2
+()
2
---------------------------------------------------
C
1
C
2
U
1
U
2
−()
2
2 C
1
C
2
+()
-------------------------------------------
C
C
C
C
0
Рис. 10.13.22
1
C
0
------
1
C
---
1
C
---
1
CC
0
+
-----------------
C 31−()
2
--------------------------
577
пройдем по цепи из точи A в точу B, например через точу a
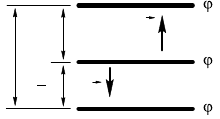
(см. в условии рис. 10.13.10). Используя потенциал ϕ
a
промежу-
точной точи a, запишем
U
A–B
= ϕ
A
– ϕ
a
+ ϕ
a
– ϕ
B
= (ϕ
A
– ϕ
a
) + (ϕ
a
– ϕ
B
).
Разность потенциалов (ϕ
A
– ϕ
a
) равна напряжению U
1
на он-
денсаторе C
1
, взятому со знаом «минус»:
ϕ
A
– ϕ
a
= –U
1
,
а разность потенциалов (ϕ
a
– ϕ
B
)— напряжению U
3
на онден-
саторе C
3
:
ϕ
a
– ϕ
B
= U
3
.
Следовательно,
U
A—B
= –U
1
+ U
3
.(1)
Для нахождения напряжения U
1
= (ϕ
a
– ϕ
A
) нужно пройти, на-
пример, по онтуру a–A–b–1 –a:
(ϕ
a
– ϕ
A
) + (ϕ
A
– ϕ
b
) – 1 = 0, (2)
де ϕ
b
— потенциал в точе b, (ϕ
A
– ϕ
b
) = U
2
— напряжение на он-
денсаторе C
2
. Для нахождения напряжения U
3
= (ϕ
a
– ϕ
B
) пройдем
по онтуру a–B–b–1 –a:
(ϕ
a
– ϕ
B
) + (ϕ
B
– ϕ
b
) – 1 = 0, (3)
де (ϕ
B
– ϕ
b
) = U
4
— напряжение на онденсаторе C
4
.
Выражения (2) и (3) можно записать в виде
U
1
+ U
2
= 1, U
3
+ U
4
= 1.(4)
Конденсаторы C
1
и C
2
соединены последовательно, поэтому за-
ряды на них одинаовы:
q
1
= q
2
, или C
1
U
1
= C
2
U
2
,(5)
q
3
= q
4
, или C
3
U
3
= C
4
U
4
.(6)
Решив систему уравнений (4)—(6), получим
U
1
= , U
2
= , U
3
= , U
4
= .
C
2
1
C
1
C
2
+
-------------------
C
1
1
C
1
C
2
+
-------------------
C
4
1
C
3
C
4
+
-------------------
C
3
1
C
3
C
4
+
-------------------
578
Подставив значения напряжений U
1
и U
3
в (1), получим
ответ:
U
A – B
= 1 .
10.13.23. Обозначим заряды на внешних обладах онденса-
торов q
1
, q
2
и q
3
соответственно. Потенциал точи O
ϕ
0
= ϕ
1
+ = ϕ
2
+ = ϕ
3
+ . (1)
Из этой системы уравнений с учетом, что q
1
+ q
2
+ q
3
= 0, находим
q
1
= .
Подставив это выражение в (1), получим о т в е т:
ϕ
0
= ϕ
1
+ = .
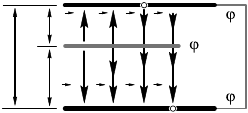
10.13.25. Тоная пластина с за-
рядом q создаст по обе стороны от
поверхностей однородные поля (рис.
10.13.23), причем
E = , (1)
что приведет появлению индуциро-
ванных зарядов на обладах онден-
сатора. Однао результирующее поле, создаваемое индуцированны-
ми зарядами, будет равным нулю. Таим образом, между облада-
ми онденсатора существует тольо поле, создаваемое внесенной
пластиной.
Если потенциал одной из обладо обозначить через ϕ
1
, а дру-
ой — через ϕ
2
, то разности потенциалов между аждой из них и
внесенной пластиной равны соответственно
ϕ – ϕ
1
= Ex = , (2)
ϕ – ϕ
2
= E(d – x) = , (3)
C
1
C
4
C
2
C
3
−
C
1
C
2
+()C
3
C
4
+()
--------------------------------------------------
q
1
C
1
------
q
2
C
2
------
q
3
C
3
------
C
1
C
2
ϕ
2
ϕ
1
−()C
2
ϕ
3
ϕ
1
−()+[]
C
1
C
2
C
3
++
---------------------------------------------------------------------------------
q
1
C
1
------
C
1
ϕ
1
C
2
ϕ
2
C
3
ϕ
3
++
C
1
C
2
C
3
++
-----------------------------------------------------
1
2
E
E
x
q
d
x
d
Рис. 10.13.23
q
2Sε
0
-------------
qx
2Sε
0
-------------
qd x−()
2Sε
0
---------------------
579
де ϕ — потенциал пластины, x и (d – x) — расстояния между плас-
тиной и обладами онденсатора.
Решив систему уравнений (1)—(3), получим о т в е т :
∆ϕ = ϕ
2
– ϕ
1
= (d – 2x).
10.13.27. Заряд Q создает по обе стороны от пластины элетриче-
сое поле напряженностью E, оторое приведет появлению индуци-
рованных зарядов. Та а облади заорочены, то заряды будут пе-
ремещаться с одной облади на друую до тех пор, поа потенциалы
пластин на станут равными ϕ
1
= ϕ
2
, причем q
1
+ q
2
= 0 (рис. 10.13.24).
Напряженность элетричесоо поля между пластиной и облад-
ой онденсатора, находящейся от нее на расстоянии d
1
= , равна
E
I
= E – E
1
– E
2
,
де E = ; E
1
= E
2
= — напряженности элетричесих по-
лей пластины и обладо соответственно.
Соответствующая разность потенциалов
ϕ – ϕ
1
= E
1
d
1
= . (1)
Для области между пластиной и второй обладой онденсато-
ра с зарядом q
2
E
II
= E + E
1
+ E
2
= ,
ϕ – ϕ
2
= E
II
d
2
= .
Та а облади соединены проводниом, то ϕ
1
= ϕ
2
. Следова-
тельно,
= , или Q – 2q = 3(Q + 2q).
q
2Sε
0
-------------
E
E
q
1
Q
E
1
E
1
E
I
E
2
E
2
E
II
q
2
d
1
d
2
1
2
d
Рис. 10.13.24
d
4
---
Q
2ε
0
S
-------------
q
2ε
0
S
-------------
Q 2q−
8ε
0
S
-----------------
Q 2q+
2Sε
0
-----------------
3 Q 2q+()d
8Sε
0
------------------------------
Q 2q−()d
8Sε
0
--------------------------
3 Q 2q+()d
8Sε
0
------------------------------
