Вакульчик В.С. Учебно-методический комплекс по высшей математике для студентов технических специальностей
Подождите немного. Документ загружается.

191
3.5.2. Производная сложной функции. Производная обратной
функции
Теорема 3.5.2. Если
(
)
u x
=ϕ
имеет производную в точке x (суще-
ствует конечная производная
x
u
′
), а
(
)
y f u
=
имеет производную в точке
(
)
u u x
=
(существует конечная производная
u
f
′
), то функция
(
)
(
)
y f u x
=
имеет производную в точке x (существует конечная производная
x
f
′
), ко-
торая определяется по формуле
x u x
dy df du
y f u
dx du dx
′ ′ ′
= = ⋅ = ⋅
(
y u x
→ →
).
Доказательство. Дадим переменной x приращение ∆x, тогда u(x)
получит приращение ∆u, а
(
)
y f u
=
получит приращение ∆y.
По условию теоремы f(u) дифференцируема в точке u(x), следова-
тельно, по теореме 3.3.1
(
)
u
y f u u u
′
∆ = ∆ +α ∆ ⋅∆
,
где
(
)
0
0
u
u
∆ →
α ∆ →
.
Вычислим
0 0
lim lim ( )
u
x
x x
f u
y u
y u
x x x
∆ → ∆ →
′
⋅∆
∆ ∆
′
= = +α ∆ ⋅ =
∆ ∆ ∆
=
( )
0 0
lim lim
u x
x x
u
f u u
x
∆ → ∆ →
∆
′ ′
+ α ∆
∆
=
( )
0
0
существует (по условию),
lim 0, 0
x
x
x
u
u u
∆ →
∆ →
′
−
⇒ ∆ = α ∆ →
=
u x
f u
′ ′
⋅
.
Теорема 3.5.3. Если функции
(
)
y y x
=
и
(
)
x x y
=
взаимно-
обратные дифференцируемые функции и
0
y
x
′
≠
, то
1
x
y
y
x
′
=
′
.
Доказательство. По условию теоремы
0
lim
y
x
x
x
y
∆ →
∆
′
∃ =
∆
,
0
lim
x
x
y
y
x
∆ →
∆
′
∃ =
∆
. Поскольку
1
y
x
x
y
∆
=
∆
∆
∆
, то
0
0
1 1
lim
lim
x
y
y
y
x
x x
y
∆ →
∆ →
∆
= =
∆
′
∆
∆
.
192
3.5.3. Таблица производных
1.
(
)
1n n
u n u u
−
′
′
= ⋅ ⋅
;
2.
1
x
′
=
;
3.
( )
1
2
u u
u
′
′
= ⋅
;
4.
2
1 1
u
u
u
′
′
= − ⋅
;
5.
( )
sin cos
u u u
′
′
= ⋅
;
6.
( )
cos sin
u u u
′
′
= − ⋅
;
7.
( )
2
1
tg
cos
u u
u
′
′
= ⋅
;
8.
( )
2
1
ctg
sin
u u
u
′
′
=− ⋅
;
9.
( )
ln
u u
a a a u
′
′
= ⋅ ⋅
;
10.
( )
u u
e e u
′
′
= ⋅
;
11.
( )
1
log
ln
a
u u
u a
′
′
= ⋅
⋅
;
12.
( )
1
ln
u u
u
′
′
= ⋅
;
13.
( )
2
1
arcsin
1
u u
u
′
′
= ⋅
−
;
14.
( )
2
1
arccos
1
u u
u
′
′
= − ⋅
−
;
15.
( )
2
1
arctg
1
u u
u
′
′
= ⋅
+
;
16.
( )
2
1
arcctg
1
u u
u
′
′
= − ⋅
+
;
17.
( )
sh ch
u u u
′
′
= ⋅
;
18.
( )
ch sh
u u u
′
′
= ⋅
;
19.
( )
2
1
th
ch
u u
u
′
′
= ⋅
;
20.
( )
2
1
cth
sh
u u
u
′
′
=− ⋅
.
- степенные
- тригонометрические
- показательные
- логарифмические
- обратнотригонометрические
- гиперболические
193
Замечание 3.5.2.
1. Формулы (1) – (12) получают, используя определение производ-
ной, (7) – (8) – используя правила дифференцирования частного, а также
производные sin x и cos x.
2. Формулы (13) – (16) получают, используя теорему о производ-
ной взаимно-обратных функций.
Выведем, например формулу 14. Рассмотрим функцию
arccos
y x
=
,
[
]
[
]
( ) 1; 1 , ( ) 0;
D y E y
= − = π
.
В
( )
D y
функция обратима:
cos
x y
=
, тогда по теореме 3.5.3
( ) ( )
[ ]
2
2
2
sin 1
1 1 1 1
1
cos sin
0; sin 1
x
y
y x
y
x
x
y y
y y x
= ± −
′
= = = − = = −
′
′ ′
−
∈ π ⇒ = −
.
Формулы 13, 15, 16 доказать самостоятельно.
Вычислить производные и дифференциалы следующих функций:
1
0
.
4
2
3
2
3
4
2 3
5 2 3 5
y x x x x
x
x
−
−
= − + = ⋅ − ⋅ + .
( )
( )
4
2
3
2 3 5y x x x
−
−
′
′
′
′
= − + =
=
( )
4
1
3
3
4 5
2 2 3
3
2
x x
x
− −
−
⋅ − ⋅ − ⋅ − ⋅ +
=
3
3
7
4 4 5
2
x
x
x
−
+ + ;
3
3
7
4 4 5
2
dy dx
x
x
x
−
= + +
.
2
0
.
2
sin
y x
= – сложная функция (участвуют степенная
2
u
и триго-
нометрическая
sin
u
).
( )
2
2
u u u
′
′
= ⋅
;
( )
2sin sin 2sin cos sin2
y x x x x x
′
′
= ⋅ = ⋅ = ;
sin2
dy xdx
=
.
3
0
.
2
cos
y x
= – сложная функция (участвуют cos u и
2
u
).
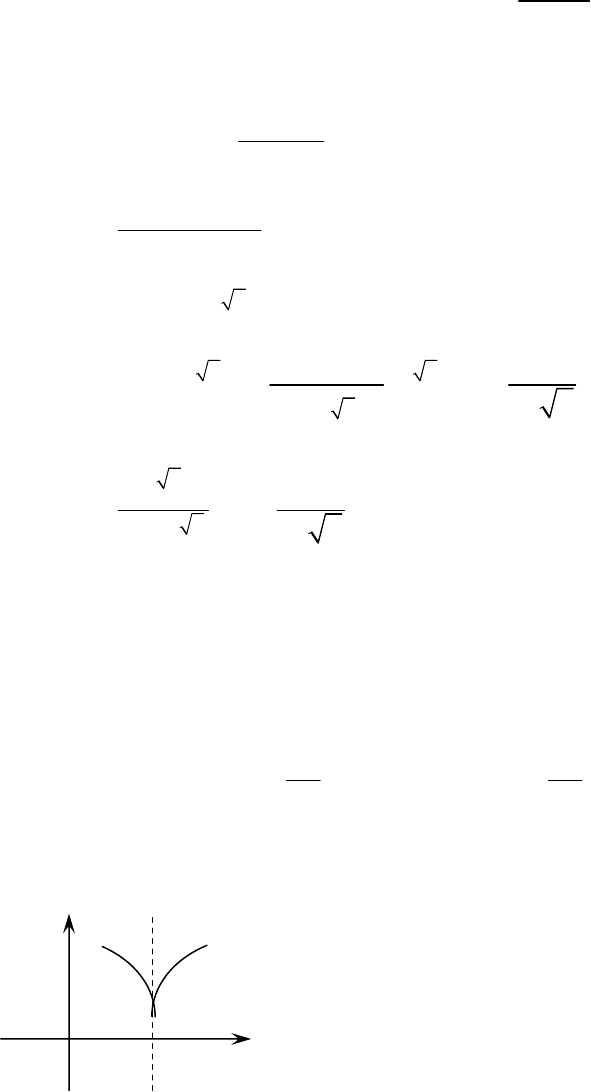
194
2 2
sin 2 2 sin
y x x x x
′
= − ⋅ = − ;
2
2 sin
dy x x dx
= − .
4
0
.
tg7
2
x
y = – участвуют производные функций:
−
−−
− показательная
( )
2 : 2 2 ln2
u u u
u
′
′
= ⋅ ⋅
;
−
−−
− тригонометрическая
( )
2
1
tg : tg
cos
u u u
u
′
′
= ⋅
;
−
−−
− линейная
7
x
:
( )
7 7
x
′
=
.
tg7
2
1
2 ln2 7
cos 7
x
y
x
′
= ⋅ ⋅ ⋅
;
tg7
2
7 ln2 2
cos 7
x
dy dx
x
⋅ ⋅
= ⋅
.
5
0
.
arctg5
x
y = .
y
′
=
(
)
(
)
2
1 1
arctg5 5 ln5 .
2
1 5
x x
x
x
′
= ⋅ ⋅ ⋅
⋅
+
2
5 1
ln5 .
2
1 5
x
x
dy dx
x
= ⋅ ⋅
⋅
+
3.6. Бесконечная производная, односторонние производные
Определение 3.6.1. Если
для
некоторого
значения
x
выполняется
одно
из
условий
0
lim
x
y
x
∆ →
∆
= +∞
∆
или
0
lim
x
y
x
∆ →
∆
= −∞
∆
,
то
говорят
,
что
в
этом
случае
в
точке
x функция имеет бесконечную
производную
.
Замечание 3.6.1. Геометрическое
истолко
-
вание
производной
как
углового
коэффициента
ка
-
сательной
к
графику
распространяется
и
на
этот
случай
:
касательная
параллельна оси
Oy
.
x
y
0

195
Определение 3.6.2. Если
отношение
y
x
∆
∆
при
0
x
∆ →
имеет
предел
справа
(
или
слева
),
то
этот
предел
называется
производной
справа
(
слева
).
Такие
пределы
называют
односторонними
и
обозначаются
:
( )
0
0
lim
x
y
f x
x
+
∆ →+
∆
′
=
∆
;
( )
0
0
lim
x
y
f x
x
−
∆ →−
∆
′
=
∆
.
Имеет
место
следующая
теорема
.
Теорема 3.6.1. Функция
(
)
y f x
=
,
определенная
в
некоторой
ок
-
рестности
точки
x
0
,
имеет
производную
(
)
0
f x
′
тогда
и
только
тогда
,
когда
(
)
(
)
0 0
f x f x
+ −
′ ′
=
.
(
)
0
f x
′
∃
⇔
(
)
(
)
0 0
f x f x
+ −
′ ′
=
.
Примеры
.
0
1
.
Доказать
,
что
функция
( )
2
, 0
sin , 0,
x x
f x
x x
<
=
≥
не
дифференцируема
в
точке
0
x
=
.
Решение
.
Первый
способ
.
Вычислим
( )
0
0
sin
0 lim 1
x
x
x
f
x
+
∆ →
∆ >
∆
′
= =
∆
;
( )
2
0
0
0 lim 0
x
x
x
f
x
−
∆ →
∆ <
∆
′
= =
∆
.
Таким
образом
,
получим
,
что
производные
слева
и
справа
различны
.
Значит
,
функция
в
точке
0
x
=
не
дифференцируема
.
Второй
способ
.
Вычислим
( ) ( )
0
0
0 sin cos 1
x
x
f x x
+
=
=
′
′
= = =
;
( )
( )
2
0
0
0 2 0
x
x
f x x
−
=
=
′
′
= = =
.
Так
как
(
)
(
)
0 0
f f
+ −
′ ′
≠
,
то
функция
в
точке
0
x
=
не
дифференцируема
.
0
2
.
Доказать
,
что
функция
( )
2
0,
если рационально
,
,
если иррационально
x
f x
x x
=
диффе
-
ренцируема
в
точке
0
x
=
.
196
Решение
.
Имеем
(
)
0 0.
f
=
Пусть
0
x
∆ →
,
пробегая
рациональ
-
ные
значения
.
Тогда
(
)
(
)
0 0
f x f x
+∆ = ∆ =
,
а
значит
,
(
)
(
)
0 0
0 0
lim lim 0
x x
f x f
f
x x
∆ → ∆ →
+∆ −
∆
= =
∆ ∆
.
Если
0
x
∆ →
,
пробегая
иррациональные
значения
,
то
(
)
2
0
f x x
+ ∆ = ∆
и
(
)
(
)
2
0 0 0
0 0
0
lim lim lim 0
x x x
f x f
f x
x x x
∆ → ∆ → ∆ →
+∆ −
∆ ∆ −
= = =
∆ ∆ ∆
.
Таким
образом
,
оба
односторонних
предела
совпадают
.
Значит
,
функция
(
)
f x
дифференцируема
при
0
x
=
.
Обратим
внимание
на
тот
факт
,
что
заданная
функция
разрывна
во
всех
точках
,
кроме
0
x
=
.
0
3
.
Показать
,
что
функция
( )
2
1
sin ,
если 0,
0, если 0
x x
f x
x
x
≠
=
=
разрывна при
0
x
=
.
При
0
x
≠
производную вычислим по формулам дифференцирова-
ния
( )
1 1
2 sin cos
f x x
x x
′
= − .
Значение производной при
0
x
=
вычислим непосредственно по оп-
ределению:
( )
( )
2
0 0
1
sin
1
lim lim sin 0
x x
x
x
f x x
x x
∆ → ∆ →
∆
∆
′
= = ∆ =
∆ ∆
,
т.к. функция
1
sin
x
∆
– ограниченная, а
0
x
∆ →
. Таким образом, функция
(
)
f x
имеет производную
x
∀ ∈
ℝ
. Однако
(
)
0
lim
x
f x
→
′
не существует, т.к.
0
1
lim 2 sin 0
x
x
x
→
⋅ =
, а
0
1
limcos
x
x
→
не существует. Отсюда следует, что произ-
водная заданной функции разрывна при
0
x
=
.
Упражнение. Показать, что следующие функции не имеют про-
изводных в указанных точках:
1.
( )
1
sin ,
если 0,
0,
если 0
x x
f x
x
x
⋅ ≠
=
=
в точке
0
x
=
.
197
2.
( )
2
2
,
если рационально,
,
если иррационально
x x
f x
x x
=
−
в любой точке, отличной
от нуля.
3.
( )
1
,
если 0,
1
0,
если 0
x
x
x
f x
e
x
≠
=
+
=
в точке
0
x
=
.
4.
( )
1
arctg ,
если 0,
0,
если 0
x x
f x
x
x
⋅ ≠
=
=
в точке
0
x
=
.
3.7. Производная функции, заданной неявно
Аналитически неявная функция задается уравнением, неразрешен-
ным относительно x или y:
(
)
, 0
F x y
=
. (3.7.1)
Теорема 3.7.1. Если функция
( )
y y x
=
, заданная неявно уравнени-
ем
( ; ) 0
F x y
=
, дифференцируема, то
x
x
y
F
y
F
′
′
= −
′
,
где
x
F
′
– производная функции
(
)
,
F x y
по переменной x в предложе-
нии, что
const
y
=
,
y
F
′
– производная
функции
(
)
,
F x y
по
переменной
y
в
предложе
-
нии
,
что
const
x
=
.
Доказательство
.
Пусть
функция
( )
y y x
=
задана
уравнением
( ; ) 0
F x y
=
.
Продифференцируем
уравнение
по
переменной
x,
считая
x
независимой
переменной
,
а
y –
зависимой
.
Тогда
будем
иметь
0
x x y x
F x F y
′ ′ ′ ′
⋅ + ⋅ =
.
Учитывая
,
что
x
x
′
= 1,
получим
x
x
y
F
y
F
′
′
= −
′
. (3.7.2)
Замечание. Для
определения
производной
функции
,
заданной
неяв
-
но
,
не
обязательно
пользоваться
формулой
(3.7.2).
В
выводе
формулы
198
(3.7.2)
указан
еще
один
способ
вычисления
производной
функции
,
задан
-
ной
неявно
:
дифференцируем
уравнение
по
переменной
x,
считая
y
функ
-
цией
,
затем
из
нового
уравнения
выражаем
x
y
′
.
1
0
.
Задана
функция
:
(
)
3
cos 3 .
xy
x y e y x
+ = + Определить
x
y
′
.
Первый
способ
.
Воспользуемся
формулой
(3.7.2).
В
нашем
случае
(
)
,
F x y
=
(
)
3
cos 3 .
xy
x y e y x
+ − +
Вычислим
x
F
′
=
(
)
2
3 sin 3
xy
x y e y y x
+ + +
;
y
F
′
=
(
)
3
sin 3 3.
xy
x e x y x
+ + +
Тогда
по
формуле
(3.7.2):
( )
(
)
( )
( )
2
3
sin 3 3
.
3sin 3
xy
x
xy
y x ye x y
y
x xe y x
+ + +
′
= −
+ + +
Второй
способ
.
Вычислим
x
y
′
,
дифференцируя
заданное
уравнение
по
переменной
x,
считая
y
функцией
,
затем
из
нового
уравнения
выразим
x
y
′
.
(
)
(
)
(
)
2 3
3 sin 3 3 1
xy
x x x
x y x y e y xy y x y
′ ′ ′
+ + + =− + ⋅ +
,
(
)
(
)
3
3 sin 3 sin 3
xy
x x x
x y e xy y y x y x
′ ′ ′
+ ⋅ + + = − +
,
( )
(
)
( )
3 2
3sin 3 sin 3 3
xy xy
x
y x xe y x y x ye x y
′
+ + + = − + − − .
Отсюда,
( )
(
)
( )
( )
2
3
sin 3 3
.
3sin 3
xy
x
xy
y x ye x y
y
x xe y x
+ + +
′
= −
+ + +
3.8. Производная функции, заданной параметрически
Теорема 3.8.1. Пусть функция
( )
y y x
=
задана параметрически
(
)
( )
,
y y t
x x t
=
=
и функции
( )
x t
,
( )
y t
дифференцируемы в области определения перемен-
ной t, тогда
t
x
t
y
y
x
′
′
=
′
. (*)
199
Доказательство. Так как
( )
y y x
=
задана параметрически, то из
первого уравнения следует:
( )
t t x
=
, из второго уравнения следует:
( ( ))
y y t x
=
– сложная функция с промежуточным аргументом t. Тогда по
теореме о производной сложной функции
x t x
y y t
′ ′ ′
= ⋅
и по теореме о про-
изводной обратной функции
1
x
t
t
x
′
=
′
. Отсюда следует, что
t
x
t
y
y
x
′
′
=
′
. Что и
требовалось доказать.
1
0
. Задана функция:
3
2
cos ,
sin .
y t
x t
=
=
Найти
x
y
′
.
Согласно формуле (*) будем иметь
( )
( )
( )
3
2
2
2
cos
3cos sin
cos 2
sin
t
x
t
t
t t
y
t t
t
′
⋅ −
′
= =
′
⋅
.
3.9. Логарифмическая производная
Определение 3.9.1. Пусть функция
( )
y f x
=
(3.9.1)
имеет производную, а также имеет смысл выражение
ln ( )
f x
. Тогда лога-
рифмируя равенство (3.9.1), получим
(
)
ln ln
y f x
=
. (3.9.2)
Дифференцируя (3.9.2), будем иметь:
[ ]
ln ( )
y
f x
y
′
′
= . (3.9.3)
Выражение, стоящее в левой части уравнения (3.9.3), называют лога-
рифмической производной.
Из (3.9.3) следует
[ ]
ln ( )
y y f x
′
′
= ⋅ .
Замечание.
1. Из (3.9.3) выразим
( ) ( ) ( )
ln ln
x x
y y f x f x f x
′ ′
′
= ⋅ =
. (3.9.4)
200
2.
С
помощью
логарифмической
производной
вычисляют
произ
-
водные
степенно
-
показательной
функции
[ ]
( )
( )
v x
y u x= ,
а
также
производ
-
ные
функций
,
которые
представляют
собой
громоздкие
выражения
,
но
по
-
сле
логарифмирования
разворачиваются
в
алгебраическую
сумму
лога
-
рифмов
более
простых
функций
.
Примеры
.
Вычислить производные функций
:
1
0
.
( )
3
7
tg
x
y x= .
Воспользуемся
формулой
(3.9.4):
( ) ( ) ( ) ( )
3 3 3
7 7 7
3
7
tg ln tg tg ln tg
x x x
y x x x x x
′
′
′
= = =
( )
(
)
( ) ( )
( )
3
7
3 3
7 7
tg ln tg ln tg
x
x x x x x
′
′
= + =
( ) ( )
3
7
4
3
7
3
2
7 1 1
tg ln tg
3 tg
cos
x
x x x x
x
x
= + ⋅
.
2
0
.
( ) ( )
( ) ( )
5 4
7
3 6
3 7
2 3 3 1
x x
y
x x
+ −
=
− +
.
( ) ( )
( ) ( )
5 4
7
3 6
3 7
ln ln
2 3 3 1
x x
y
x x
+ −
= =
− +
( ) ( ) ( ) ( )
( )
1
5ln 3 4ln 7 3ln 2 3 6ln 3 1
7
x x x x
= + + − − − − +
.
Тогда, согласно формуле (3.9.4),
( ) ( )
( ) ( )
5 4
7
3 6
3 7
2 3 3 1
x x
y
x x
+ −
′
= ×
− +
( ) ( ) ( ) ( )
( )
1
5ln 3 4ln 7 3ln 2 3 6ln 3 1
7
x x x x
′
× + + − − − − + =
( ) ( )
( ) ( )
5 4
7
3 6
3 7
1 5 4 3 6
7 3 7 2 3 3 1
2 3 3 1
x x
x x x x
x x
+ −
= + − −
+ − − +
− +
.
