Вакульчик В.С. Учебно-методический комплекс по высшей математике для студентов технических специальностей
Подождите немного. Документ загружается.

251
Домашнее задание
1.
Изучить
тему
«
Дифференцирование
параметрически
заданных
и
неявных
функций
.
Производные
высших
порядков
».
2.
Найдите
производные
функций
:
1)
1
arctg
sh
y
x
=
.
Ответ
:
( )
2 2
ch
2 sh 1 sh
x
x x x
−
⋅ ⋅ +
;
2)
( )( )
2
sin
5
1
5 arcsin3 2 2
lntg
x
y x x x
x
= + − − + +
.
Ответ
:
( )
2
sin
2 2
2 4
2
5
3 2 1 1 1
5 ln5 sin2
tg
ln tg cos
1 9
5 4
x
x
x
x
x x
x
x
⋅ ⋅ + − − ⋅ ⋅
−
⋅ −
;
3)
1
arctg
sh
y
x
=
.
Ответ
:
( )
2 2
ch
2 sh 1 sh
x
x x x
−
⋅ ⋅ +
;
4)
( )
ln tg
tg
x
y x= .
Ответ
:
( )
lntg
2lntg
tg
cos sin
x
x
x
x x
⋅
;
5)
( )
3
2
4
1 3
y x
= + .
Ответ
:
( )
2
4
9
2 1 3
x
x
+
;
6)
2
cos sin
3
x
y
=
.
Ответ
:
1
sin 2sin cos
3 3 3
x x
− ⋅
.
3.
Выполнить
первую
часть
из
внеаудиторной
контрольной
работы
.
III. Дифференцирование параметрически заданных и неявных
функций. Производные высших порядков
1. Производная функции, заданной неявно
Если
функция
(
)
y x
задана
неявно
уравнением
(
)
, 0
F x y
=
,
то
для
вычисления
ее
производной
надо
продифференцировать
это
уравнение
по
x,
считая
y
функцией
от
x,
и
решить
полученное
уравнение
относительно
(
)
y x
′
.
Для
вычисления
(
)
y x
′
можно
использовать
также
формулу
x
x
y
F
y
F
′
′
= −
′
.

252
Обучающая задача. Найти
производную
dy
dx
в
точке
М
0
(–2; 1)
функции
у
(
х
),
заданной
неявно
уравнениями
:
1
0
.
3 2 2
0
x x y y
+ + =
; 2
0
.
ln 3
y y x
= +
.
Решение
.
1
0
.
Первый
способ
:
дифференцируем
уравнение
по
x,
считая
y
функцией
от
x:
( )
2 2 2
3 2 0
x x y x y y y
′
′ ′
+ ⋅ + ⋅ + ⋅ =
⇒
(
)
2 2
3 2 2 0
x xy y x y y
′ ′
+ + + ⋅ =
,
2
2
3 2
2
x xy
y
x y
+
′
= −
+
,
( )
( )
( ) ( )
( )
2
0
2
3 2 2 2 1
4
2; 1
3
2 2 1
y M y
− + − ⋅
′ ′
= − = − = −
− + ⋅
.
Второй способ:
2
3 2
x
F x xy
′
= + ;
2
2
y
F x y
′
= +
;
2
2
3 2
2
x
x xy
y
x y
+
′
= −
+
.
2
0
. Дифференцируем уравнение по x
1
ln 1
y y y y
y
′ ′
⋅ + ⋅ ⋅ =
⇒
ln 1
y y y
′ ′
⋅ + =
⇒
(
)
ln 1 1
y y
′
+ =
,
1
ln 1
y
y
′
=
+
⇒
( )
0
1
1
ln1 1
y M
′
= =
+
.
Но у′ можно было найти по-другому, используя формулу производ-
ной обратной функции:
ln 3
x y y
= −
⇒
1
ln
y
x y y
y
′
= + ⋅
⇒
ln 1
y
x y
′
= +
⇒
1 1
ln 1
x
y
y
x y
′
= =
′
+
.
Выполнить (самостоятельно, каждому свой вариант, два студен-
та у доски выполняют свои задания, по желанию третий уровень вы-
полняется у доски для получения оценки «10»).
Уровень I
Найти производную
dy
dx
в точке
(
)
0 0 0
;
M x y
.
1)
3 2 2
2 5 5 0
x x y x y
− + + − =
,
(
)
0
1;1
M .
Ответ:
2 2
2
3 4 5
1 4
x xy
x y
− +
−
−
,
( )
1
1;1
3
x
y
′
=
;

253
2)
2 3 2
5 0
x xy y
+ − − =
,
(
)
0
1; 2
M .
Ответ:
3
2
2
3 2
x y
xy y
+
−
−
,
(
)
1;2 1,25
x
y
′
= −
;
3)
3
2 1 0
y xy
− − =
,
(
)
0
1;1
M .
Ответ:
3
2
y
,
(
)
1;1 0,5
x
y
′
=
;
4)
( ) ( )
3
27 0
x y x y
+ − − =
,
(
)
0
2;1
M .
Ответ:
( )
( )
2
2
9
9
x y
x y
+ −
+ +
,
(
)
2;1 0
x
y
′
=
;
5)
3 2 2
1 0
x x y y
+ + − =
,
(
)
0
0;1
M .
Ответ:
2
2
3 2
2
x xy
x y
+
−
+
,
(
)
0;1 0
x
y
′
=
;
6)
( )
2
2 2 2
1
x y x x y
+ + + =
,
(
)
0
0;1
M .
Ответ:
(
)
( )
2
2
x xy x y
xy x y
+ + +
−
+ +
,
(
)
0;1 1
x
y
′
= −
;
7)
( ) ( )
2
2
0
x x y x y
+ − − =
,
(
)
0
1; 0
M .
Ответ:
( ) ( )
( )
2
2
2
2 2 1
2 1
x x y x x y
x x y
+ + + −
−
+ +
,
( )
1
1;0
3
x
y
′
=
;
8)
( )
2
3 2
2 8 0
x y x y
− + + =
,
(
)
0
1;1
M .
Ответ:
(
)
( )
2 2
3
3 4 2
2 2 2
x y x y
x y x y
− +
−
− +
,
(
)
1;1 2,25
x
y
′
= −
;
9)
5 5
2 0
x y xy
+ − =
,
(
)
0
1;1
M .
Ответ:
5
5
5 2
5 2
x x
y y
−
−
−
,
(
)
1;1 1
x
y
′
= −
;
10)
4 4
4 6 0
y x xy
− − =
,
(
)
0
1; 2
M .
Ответ:
3
3
2 3
8 3
y y
x x
−
+
,
( )
2
1;2
11
x
y
′
= −
;
254
11)
(
)
2
2
4
x y x y
+ + − =
,
(
)
0
1;1
M .
Ответ:
(
)
( )
2
2
2 1
4 1
x y
y x y
+ +
−
+ −
,
( )
5
1;1
7
x
y
′
= −
;
12)
(
)
2
3 3
2 2
x y y
+ − =
,
(
)
0
1;1
M .
Ответ
:
(
)
( )
2 3 3
2 3 3
3
3 2
x x y
y x y
+
−
+ −
,
(
)
1;1 1,5
x
y
′
=
;
13)
(
)
2
2 2
12 1
x y y
+ − =
,
(
)
0
1; 2
M .
Ответ
:
(
)
( )
2 2
2 2
3
x x y
y x y
+
+ −
,
( )
5
1;2
7
x
y
′
= −
;
14)
4 4
1
x y xy
+ − =
,
(
)
0
1;1
M .
Ответ
:
3
3
4
4
x y
y x
−
−
−
,
(
)
1;1 1
x
y
′
= −
;
15)
4 3
1
x y xy
+ − =
,
(
)
0
1;1
M .
Ответ
:
3
2
4
3
x y
y x
−
−
−
,
(
)
1;1 1,5
x
y
′
= −
.
Уровень II
Найти
производную
dy
dx
в
точке
(
)
0 0 0
;
M x y
.
1)
y
e xy e
+ =
,
(
)
0
0;1
M .
Ответ
:
y
y
e x
−
+
,
( )
1
0;1
x
y
e
′
= −
;
2)
2
ln
y
y x
x
= + ,
(
)
0
1;1
M .
Ответ
:
(
)
( )
1
2 1
y x
x y
−
−
,
(
)
1;1 0
x
y
′
=
;
255
3)
1
y x
ye e
+
= ,
(
)
0
0;1
M .
Ответ
:
( )
1
1
x
y
e
e y
+
−
+
,
(
)
0;1 0,5
x
y
′
= −
;
4)
2 ln
2
yx
y x
= +
,
(
)
0
1; 2
M .
Ответ
:
(
)
( )
2 1
1
y x
x y
+
−
,
(
)
1;2 6
x
y
′
=
;
5)
tg
y xy y
= −
,
(
)
0
2; 0
M .
Ответ
:
2
2 2
cos
1 cos cos
y y
x y y
⋅
− ⋅ +
,
(
)
2;0 0
x
y
′
=
;
6)
2
2
y
xe x y
= + −
,
(
)
0
2; 0
M .
Ответ
:
2
1
y
y
x e
x e
−
−
− ⋅
,
(
)
2;0 3
x
y
′
=
;
7)
ln
y
x
x
x e
e
−
+ =
,
(
)
0
1;1
M .
Ответ
:
1
2
1
y
x
y
x
e x y e x
e
− +
− +
⋅ − ⋅ −
,
(
)
1;1 1
x
y e
′
= −
;
8)
2
x y
e xy
−
+ =
,
(
)
0
1;1
M .
Ответ
:
2
2
x y
x y
xy e y
x xy e
−
−
⋅ +
− ⋅
,
(
)
1;1 3
x
y
′
= −
;
9)
arctg
x
xy
y
= ,
(
)
0
1;1
M .
Ответ
:
(
)
( )
2 2
2 2
1
1
y x y
x x y
− −
+ +
,
( )
1
1;1
3
x
y
′
= −
;
10)
(
)
2
tg 4
xy x y
= − +
,
(
)
0
0;1
M .
Ответ
:
(
)
( )
2
2
cos
2 cos
xy y
y xy x
−
+
,
(
)
0;1 1
x
y
′
=
;
256
11)
2 2
sin 4
x y xy
+ + =
,
(
)
0
2; 0
M .
Ответ
:
(
)
( )
2 cos
2 cos
x y xy
y x xy
+
−
+
,
(
)
2;0 2
x
y
′
= −
;
12)
( )
arctg 1
4
y x y x
π
+ + = + −
,
(
)
0
1; 0
M .
Ответ
:
( )
( )
2
2
1
x y
x y
+
+ +
,
(
)
1;0 0,5
x
y
′
=
;
13)
(
)
2
arcsin 1
xy x
+ =
,
(
)
0
1; 0
M .
Ответ
:
2 2
2 1
y x x y
x
+ −
− ,
(
)
1;0 2
x
y
′
= −
;
14)
(
)
2
ln 1
xy y
+ =
,
(
)
0
1;1
M .
Ответ
:
( )
2
1 2
y
x y
−
+
,
( )
1
1;1
3
x
y
′
= −
;
15)
2
4 8
xy y
− = −
,
(
)
0
1; 4
M .
Ответ
:
y
y xy x
−
,
( )
4
1;4
7
x
y
′
=
.
Уровень III
Определить
под
каким
углом
пересекаются
кривые
2 2
4 1
x y x
+ − =
,
2 2
2 9
x y y
+ + =
.
Ответ
:
в
точке
(1; 2)
45
ϕ= °
;
2. Производная функции, заданной параметрически
Обучающая задача. Составить
уравнение
касательной
к
окружно
-
сти
2cos
2sin
x t
y t
=
=
в
точке
,
соответствующей
значению
параметра
0
3
4
t
π
= .
Сделать
чертеж
.
Если
(
)
y t
′
∃
,
(
)
0
x t
′
≠
,
то
t
x
t
y
y
x
′
′
=
′
или
dy
dy
dt
dx
dx
dt
= .
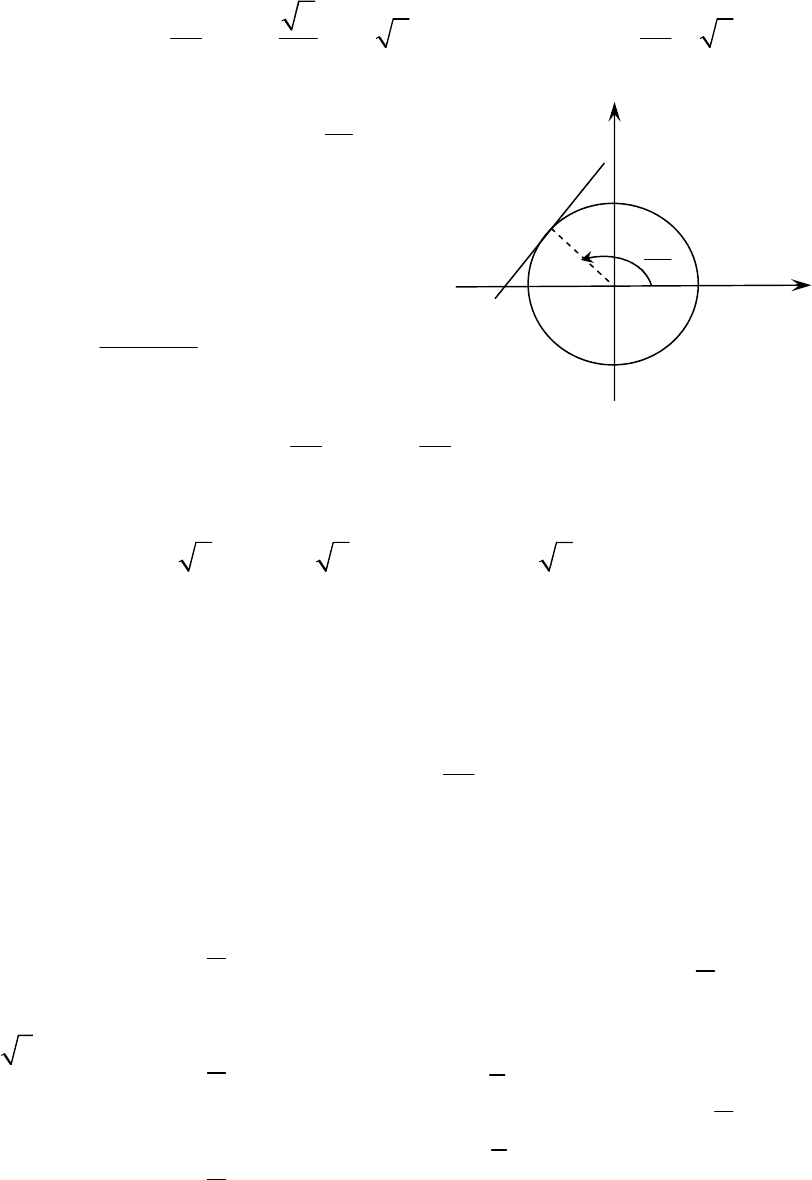
257
Решение
.
Уравнение
касательной
к
кривой
имеет
вид
(
)
(
)
0 0 0
y y y x x x
′
− = −
.
Найдем
координаты
точки
касания
(
)
0 0 0
;
M x y
и
угловой
коэффициент
касательной
(
)
0
y x
′
:
( )
0 0
3 2
2cos 2 2
4 2
x x t
π
= = = − = −
,
( )
0 0
3
2sin 2
4
y y t
π
= = = .
Производная
x
y
′
,
равная
t
t
y
x
′
′
,
есть
функция
параметра
t,
поэтому
(
)
(
)
0 0
x x
y x y t
′ ′
=
.
В
нашем
случае
( )
( )
2sin
ctg
2cos
x
t
y t
t
′
′
= = −
′
,
3 3
ctg 1
4 4
x
y
π π
′
= = − =
.
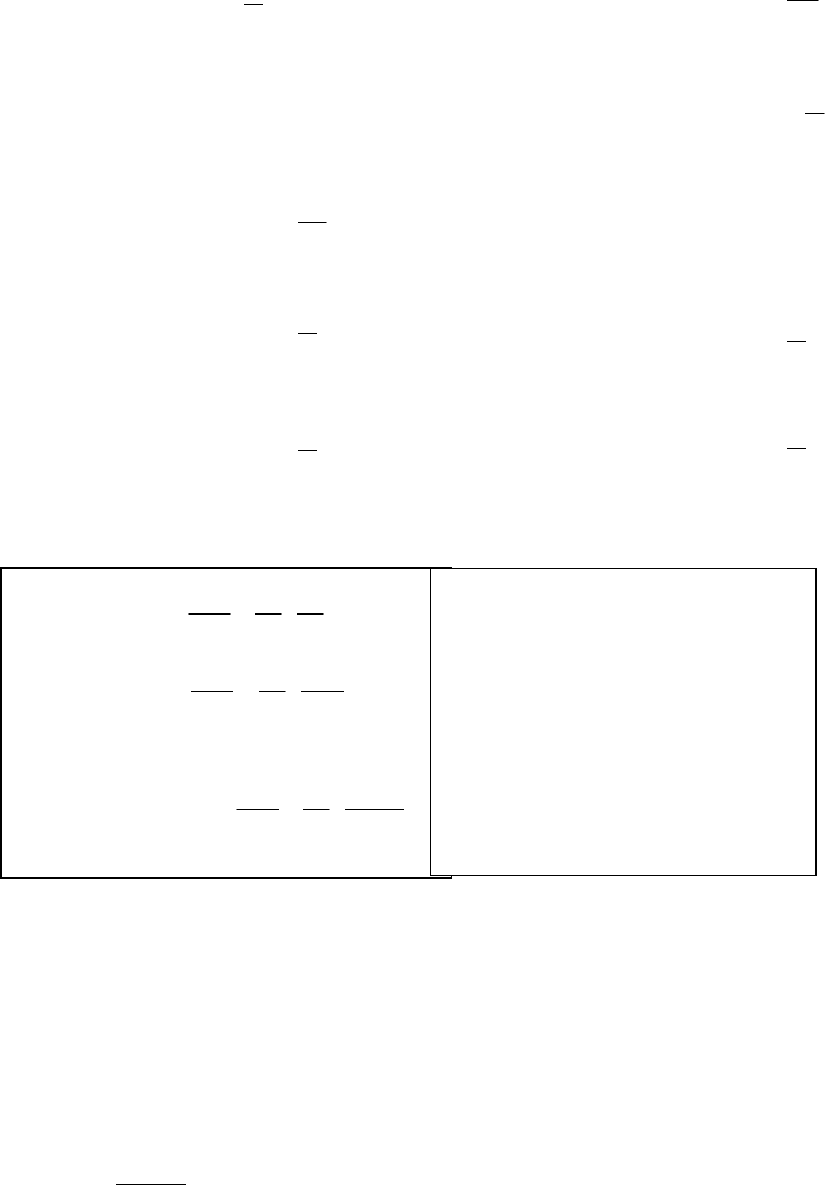
Составляем уравнение касательной
(
)
2 1 2
y x− = ⋅ + или
2 2
y x= + .
Выполнить (самостоятельно, каждому свой вариант, два студен-
та у доски выполняют свои задания, по желанию третий уровень вы-
полняется у доски для получения оценки «10»).
Упражнение. Найти производную
dy
dx
в точке
0
t
от функции, за-
данной параметрически. Составить уравнение касательной к кривой в точ-
ке, соответствующей значению параметра
0
t
. Сделать чертеж.
1)
3
3
sin
cos ,
x t
y t
=
=
0
3
t
π
=
;
2)
3cos
sin ,
x t
y t
=
=
0
3
t
π
=
;
3)
( )
sin
1 cos ,
x t t
y t
= −
= −
0
3
t
π
=
;
4)
cos2
4sin2 ,
x t
y t
=
=
0
4
t
π
=
;
5)
3
3
1
sin
3
1
cos ,
3
x t
y t
=
=
0
4
t
π
= −
;
y
x
0
3
4
π
M
0
2
258
6)
(
)
( )
4 sin
4 1 cos ,
x t t
y t
= −
= −
0
2
t
π
=
;
7)
sin3
cos3 ,
x t
y t
=
=
0
0
t
=
;
8)
2cos4
4sin4 ,
x t
y t
=
=
0
16
t
π
=
;
9)
(
)
( )
2 sin
2 1 cos ,
x t t
y t
= −
= −
0
4
t
π
=
;
10)
3
3
8cos
8sin ,
x t
y t
=
=
0
4
t
π
=
;
11)
2cos
4sin ,
x t
y t
=
=
0
3
4
t
π
= ;
12)
3
3
2cos
2sin ,
x t
y t
=
=
0
4
t
π
= −
;
13)
(
)
( )
3 sin
3 1 cos ,
x t t
y t
= −
= −
0
t
= π
;
14)
3sin2
3cos2 ,
x t
y t
=
=
0
6
t
π
=
;
15)
6cos
2sin ,
x t
y t
=
=
0
3
t
π
=
;
3. Понятие производной высшего порядка. Формула Лейбница
Обучающая задача. Найти n-ную производную от функций:
1
0
.
x
y e
−
= .
Решение: Имеем
( )
( )
x x x
y e e x e
− − −
′
′
′
= = ⋅ − = −
. Тогда
( )
x x
y e e
− −
′
′′
= − = ,
( )
x x
y e e
− −
′
′′′
= = −
,
( )
( )
4
x x
y e e
− −
′
= − = и т.д.
Следовательно
(
)
( )
1
n
n
x
y e
−
= − .
2
0
.
1
5 3
y
x
=
+
.
Решение:
Находим
( )
(
)
( ) ( ) ( )
1 2 2
5 3 5 3 5 3 5 5 3
y x x x x
− − −
′
′
′
= + = − + ⋅ + = − + .
( )
2
2
d y d dy
y y
dx dx
dx
′
′′ ′
= ⇔ =
,
( )
3 2
3 2
d y d d y
y y
dx
dx dx
′
′′′ ′′
= ⇔ =
,
…….………………………,
( ) ( )
(
)
1
1
1
n n
n n
n n
d y d d y
y y
dx
dx dx
−
−
−
′
= ⇔ =
.
Закон движения точки в
3
R
:
(
)
(
)
(
)
(
)
r t x t i y t j z t k
= + +
Вектор скорости в момент
времени t:
(
)
(
)
(
)
(
)
r t x t i y t j z t k
= + +
ɺ
ɺ ɺ
ɺ
Вектор ускорения
в момент времени t:
(
)
(
)
(
)
(
)
r t x t i y t j z t k
= + +
ɺɺ
ɺɺ ɺɺ
ɺɺ
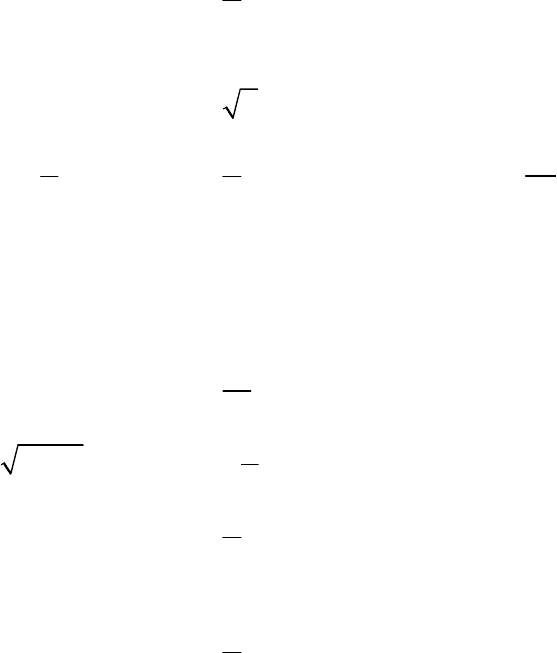
259
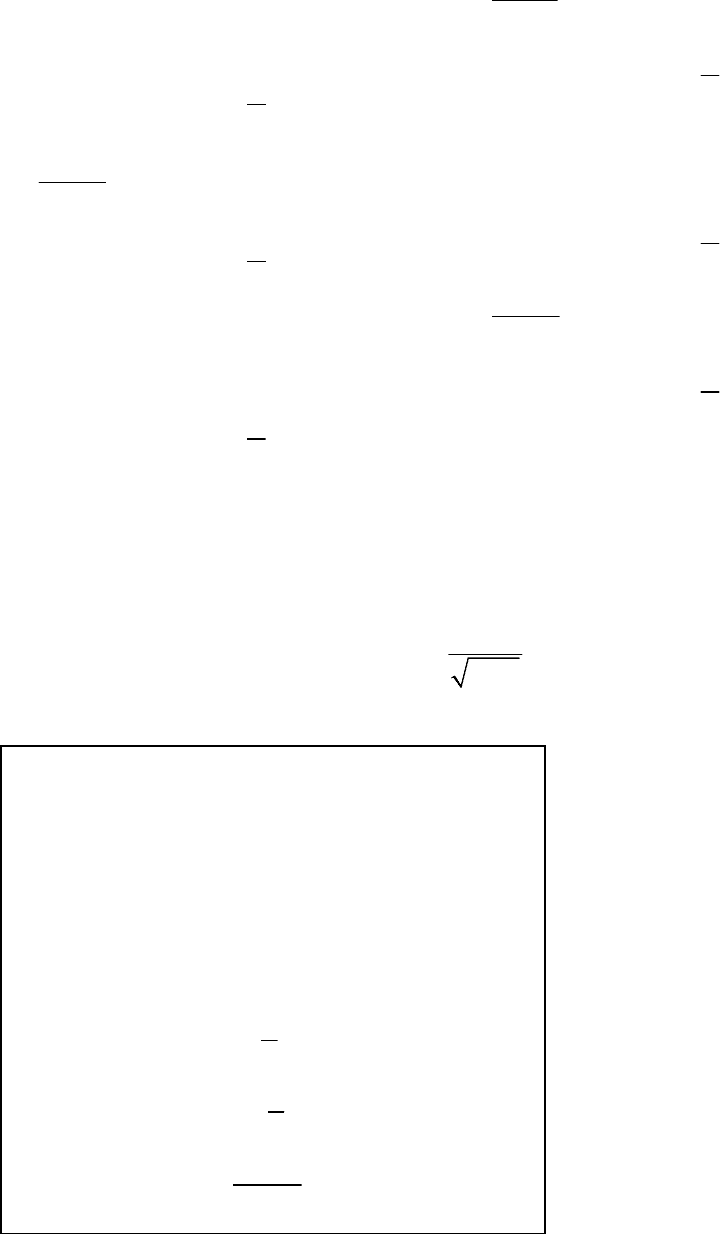
( )
(
)
( ) ( )
2 3 3
2 2
5 5 3 2 5 5 3 2! 5 5 3
y x x x
− − −
′
′′
= − + = ⋅ + = ⋅ ⋅ + ,
( ) ( ) ( )
4 4
3 4
2! 3 5 5 3 3! 5 5 3
y x x
− −
′′′
= ⋅ − ⋅ ⋅ + = − ⋅ ⋅ + ,
(
)
( )( ) ( )
5 5
4
3 4
3! 5 4 5 3 4! 5 5 3
y x x
− −
= − ⋅ ⋅ − + = ⋅ ⋅ + .
Тогда
(
)
( ) ( )
(
)
1
1 ! 5 5 3
n n
n
n
y n x
− +
= − ⋅ ⋅ + .
Выполнить (самостоятельно, каждому свой вариант, два студен-
та у доски выполняют свои задания, по желанию третий уровень вы-
полняется у доски для получения оценки «10»).
Уровень I
Найдите
(
)
0
y x
′′
1)
2
x
y e
−
= ,
0
0
x
=
. Ответ: {-2};
2)
2
cos
y x
= ,
0
2
x
π
=
. Ответ: {2};
3)
2
ln
y x
= ,
0
x e
=
. Ответ: {0};
4)
2
sin
y x
= ,
0
x
= π
. Ответ: {-2};
5)
1
cos
y
x
= ,
0
2
x
=
π
. Ответ:
3
4
π
;
6)
tg
y x
=
,
0
0
x
=
. Ответ: {0};
7)
arcsin2
y x
=
,
0
0
x
=
. Ответ: {0};
8)
2
cos2
y x
= ,
0
0
x
=
. Ответ: {0};
9)
2
cos 2
y x
= ,
0
12
x
π
=
. Ответ: {-4};
10)
1 2
y x
= − ,
0
3
2
x
= −
. Ответ: {-0,125};
11)
ctg
y x
=
,
0
2
x
π
=
. Ответ: {0};
12)
lncos2
y x
=
,
0
x
= π
. Ответ: {-4};
13)
cossec
y x
=
,
0
2
x
π
=
. Ответ: {1};
14)
2
sin
y x
= ,
0
0
x
=
. Ответ: {0};
15)
sec
y x
=
,
0
0
x
=
. Ответ: {1}.
260
Уровень II
Найдите
(
)
( )
10
0
y x
1)
2
x
y e
−
= ,
0
0
x
=
;
2)
(
)
ln 1 2
y x
= +
,
0
0
x
=
;
3)
cos2
y x
=
,
0
2
x
π
=
;
4)
1
1 2
y
x
=
−
,
0
0
x
=
;
5)
sin2
y x
=
,
0
4
x
π
=
;
6)
3
x
y e
−
= ,
0
0
x
=
;
7)
(
)
ln 1 3
y x
= +
,
0
0
x
=
;
8)
cos3
y x
=
,
0
3
x
π
=
;
9)
1
1 3
y
x
=
−
,
0
0
x
=
;
10)
sin3
y x
=
,
0
6
x
π
=
;
11)
4
x
y e
−
= ,
0
0
x
=
;
12)
(
)
ln 1 4
y x
= +
,
0
0
x
=
;
13)
cos4
y x
=
,
0
4
x
π
=
;
14)
1
1 4
y
x
=
−
,
0
0
x
=
;
15)
sin4
y x
=
,
0
8
x
π
=
;
16)
(
)
ln 1
y x
= −
,
0
2
x
=
.
Уровень III
Найдите
(
)
( )
n
y x
.
1)
(
)
2
ln 2
y x x
= + −
; 2)
1
1
x
y
x
+
=
−
.
4.
1.
(
)
(
)
2
ln , ln ,
x x x x
a a a a a a
′ ′′
= =
…
,
(
)
(
)
(
)
(
)
ln ,
n n
x x n x x
a a a e e
= =
;
2.
(
)
1
m m
x mx
−
′
=
,
(
)
( )
2
1
m m
x m m mx
−
′′
= ⋅ −
, …,
(
)
(
)
( )( ) ( )
1 2 1
n
m m n
x m m m m n mx
−
= − − − +
…
;
3.
( )
( )
sin sin
2
n
x x n
π
= + ⋅
;
4.
( )
( )
cos cos
2
n
x x n
π
= + ⋅
;
5.
( )
( )
( )
(
)
1
1 !
ln 1
n n
n
n
x
x
−
−
= − ⋅
.
