Вернер М. Основы кодирования
Подождите немного. Документ загружается.


7.5.
Пропускная
способность
канала
(03 ,
Источник
X
Источник
Y
l-p-q
Jt,="O"
Уз="1"
Рис.
7.12.
Двоичный
симметричный
канал
со
стираниями.
Обозначим вероятность стирания через q, а вероятность ошибки
нестертого символа через р.
Диаграмма переходов для канала с двумя входными и тремя вы-
ходными символами приведена на рис. 7.12. Соответствующая мат-
рица
канала, содержащая переходные вероятности, имеет вид
рдскс /1-Р-? яр \
(750)
Y/X \ p q 1 -, р - д. J
Найдем пропускную снособность канала со стираниями. Так как ка-
нал симметричен, пропускная снособность достигается при равно-
мерном распределении
входных
символов
=
1/2.
(7.51)
Отсюда
следует,
что вероятности выходных символов равны
РЫ
=
-^~,РЫ
=
Я,р{Уъ)
= ~^г-
(7.52)
Теперь все необходимые вероятности известны. Воспользовавшись
(7.9), имеем
О«™
ЛЛ. .. *нЫ
(7
.
53)
бит
*
3
2
3
» 3
Используя свойство симметрии канала, получаем

Глава
7. Дискретные каналы без памяти
QJXCKC
бит
к r
/
г, \
(7.54)
1
— р — I
1-9
Как
мы
видим,
пропускная
способность
канала
со
стираниями
зави-
сит
только
от
вероятностей
р и q.
График
С =
/(р,
9) представляет
собой
пространственную
трехмерную поверхность, расположенную
над
плоскостью
(p,q).
Здесь
мы
ограничимся
только
рассмотрением
двух важных частных случаев.
1. При 9 = 0, мы
имеем
двоичный
симметричный
канал,
уже рас-
смотренный
ранее.
Подставляя
q = 0 в (7.59) мы, как и ожидалось,
получаем
(7.49).
2.
В
канале
присутствуют
только
стирания,
т.е. при р = 0 -
ошиб-
ки
или не присутствуют, или мы ими
пренебрегаем.
В
этом
случае
С
дскс
= (1 - q) бит. (7.55)
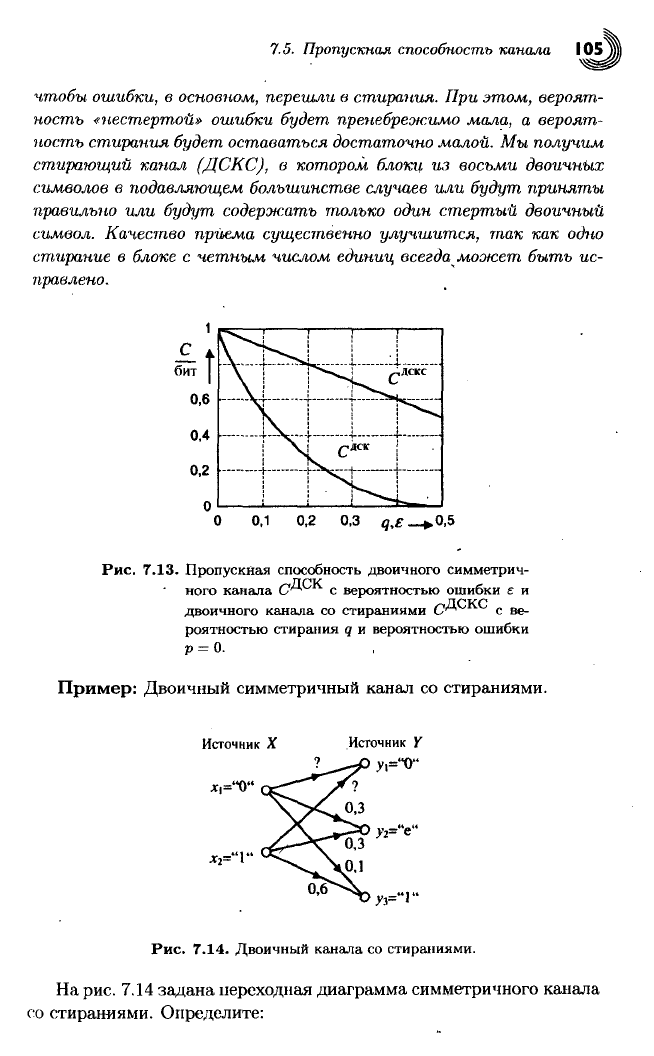
На
рис.
7.13
показаны
пропускные
способности
ДСК (7.49) и дво-
ичного
канала
со
стираниями
(р = 0).
Нужно
отметить, что при ма-
лых
вероятностях
ошибки,
выбором
оптимальных
областей
стираний
в
ДСКС
можно
достичь существенно больших
пропускных
способ-
ностей,
чем в обычных двоичных
каналах.
Замечание.
Здесь возникает вопрос о возможности увеличения
пропускной способности при приеме со стираниями на
практике.
В.
этом месте обнаруживается слабость теории информации. Тео-
рия информации зачастую не может предложить конструкцию,
реализующую теоретически достижимые границы. Тем не менее,
небольшой пример,
подробно
рассмотренный во второй части этой
книги,
показывает,
что введение
стираний
может
иногда
снижать
вероятность ошибки. Рассмотрим этот пример на интуитивном
уровне. Разобьем поток передаваемой информации на блоки,
содер-
жащие 7 двоичных символов (7 бит). К каждому блоку добавим
один бит
(•«в»
или «1*) проверки на четность.
Закодированные
та-
ким
образом
блоки из восьми двоичных символов всегда будут со-
держать четное число единиц. Пусть вероятность ошибки в ДСК
достаточно мала. Введем зону стирания (рис.7.11) таким образом,
7.5.
Пропускная
способность
канала
чтобы
ошибки,
в основном, перешли в стирания. При этом, вероят-
ность «нестертой» ошибки будет пренебрежимо мала, а вероят-
ность стирания будет оставаться
достаточно
малой. Мы получим
стирающий
канал
(ДСКС), в котором блоки из восьми двоичных
символов в подавляющем большинстве случаев или будут приняты
правильно или будут содержать только один стертый двоичный
символ.
Качество приема существенно улучшится, так как
одно
стирание в блоке с четным числом единиц всегда может быть ис-
правлено.
бит
0,6
0,4
0,2
0
0,1 0,2 0,3 q,E.
•
0,5
Рис.
7.13.
Пропускная способность двоичного симметрич-
ного канала
С^ с
вероятностью ошибки
е и
двоичного канала
со
стираниями
С^ с ве-
роятностью стирания
q и
вероятностью ошибки
р
= 0.
Пример:
Двоичный симметричный канал
со
стираниями.
Рис.
7.14.
Двоичный канала
со
стираниями.
На
рис.
7.14
задана переходная диаграмма симметричного канала
со стираниями. Определите:

1
106
Глава
7.
Дискретные
каналы
без
памяти
1. Матрицу канала ;
2. Распределение вероятностей символов источника Y, если из-
вестно, что символы источника X равномерно распределены,
т.е. р
0
= pi = 1/2;
3. Пропускную способность канала;
4. Диаграмму информационных потоков со всеми энтрониями;
5. Модель канала с матрицей Рх/у-
Решение.
1. С
учетом
того, что сумма вероятностей в каждой строке мат-
рицы
равна 1, получим
р
дскс_ /0,6 0,3 0,1
р
у/* -l,o,i о.з 0,6
2. Исходя из равномерного распределения вероятностей символов
на
входе,
согласно (7.52), имеем
рЫ=
0,35, рЫ = 0,ЗирЫ=0,35.
(7.57)
3. Так как рассматриваемый канал симметричен, пропускная спо-
собность достигается при равномерном распределении
входных
сим-
волов. Из
(7.54)
с
учетом
(7.56)
имеем
1 _ п ч _ п 1
-0,3
+
(l-0,3-0,l)ky
a
^^
+
(7.58)
4. Энтропия дискретного двоичного источника без памяти X с
равномерным распределением вероятностей символов равна
Н(Х) = 1 бит.
(7.59)
Энтропия
источника Y равна
tf(Y)
бит
=
-2 • 0,35
log
2
0,35 - 0,35
log
2
0,3 «
1,5813.
(7.60)
Так
как в симметричном канале с равномерным распределени-
ем
входных
символов I(X;Y) совпадает с пропускной способностью
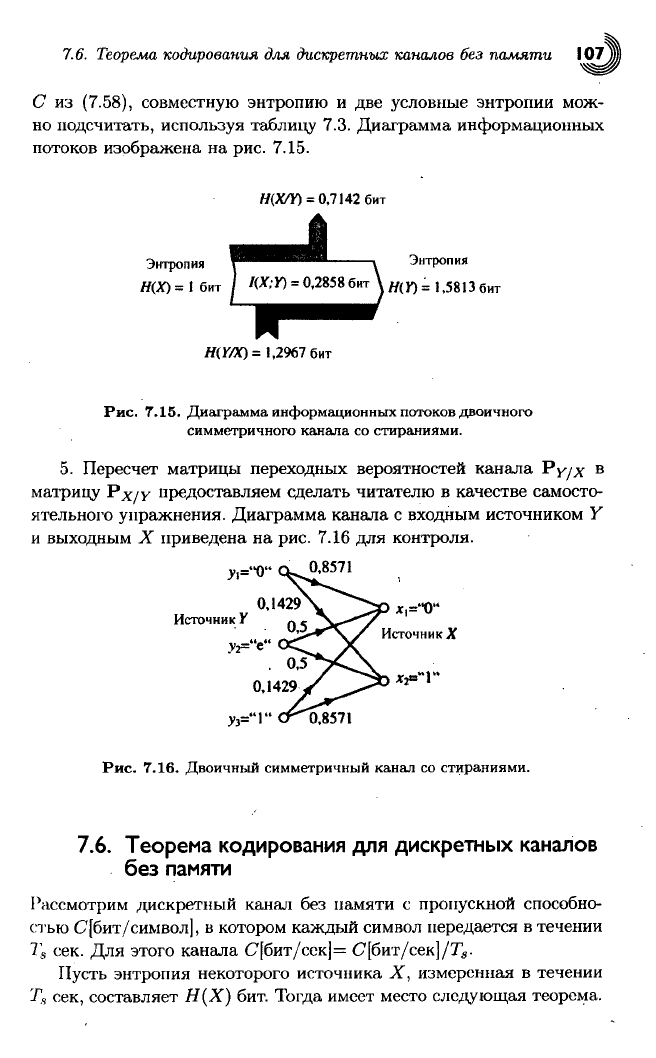
7.6. Теорема кодирования для дискретных каналов без памяти 107)
С
из
(7.58), совместную энтропию
и две
условные энтропии мож-
но
подсчитать, используя таблицу 7.3. Диаграмма информационных
потоков
изображена
на
рис.
7.15.
Н(ХЛГ)
=
0,7142
бит
Энтропия
^ .
Энтропия
//(*)=
I бит /
/№)0 =
0,2858бит
\
W(
y)
=1
5813бит
)=
1,2967 бит
Рис.
7.15.
Диаграмма
информационных потоков
двоичного
симметричного
канала
со
стираниями.
5. Пересчет матрицы переходных вероятностей канала
Ру/х
в
матрицу
Px/Y
предоставляем сделать читателю
в
качестве самосто-
ятельного упражнения. Диаграмма канала
с
входным источником
У
и
выходным
X
приведена
на
рис. 7.16 для контроля.
0,8571
дг,="О"
Источник
X
0,1429.
Уз="1"
С^"0,8571
Рис.
7.16.
Двоичный
симметричный
канал
со
стираниями.
7.6.
Теорема
кодирования
для дискретных каналов
без
памяти
Рассмотрим
дискретный канал
без
памяти
с
пропускной способно-
стью С[бит/символ],
в
котором каждый символ передается
в
течении
7'
s
сек. Для этого канала С[бит/сек]= С[бит/сек]/Г«.
Пусть энтропия некоторого источника
X,
измеренная
в
течении
Т
я
сек, составляет
Н(Х)
бит. Тогда имеет место следующая теорема.

Глава
7.
Дискретные
каналы без
памяти
Теорема 7.6.1.
Теорема
кодирования
для канала (теорема Шенно-
на).
Для источника X со скоростью R — H(X)/T
S
[бит/сек] и R < С
существует
некоторый код, с помощью которого информация источ-
ника
X может быть передана.но каналу связи с пропускной способ-
ностью С[бит/сек] со сколь угодно малой вероятностью ошибки.
1
Доказательство теоремы кодирования для канала (см..например,
[10]) довольно сложно и выходит за рамки этой книги, поэтому огра-
ничимся
здесь следующими замечаниями.
• Доказательство теоремы кодирования предполагает использо-
вание случайных кодов бесконечной длины и декодера макси-
мального правдоподобия, обеспечивающего минимальную ве-
роятность ошибки. Доказательство не использует никаких кон-
структивных решений. В нем используются только статисти-
ческие свойства и предельные переходы для блоковых кодов с
длиной блоков, стремящейся к бесконечности. Доказательство
не
дает
никаких указаний на конструкцию оптимальных кодов.
• Теорема кодирования определяет также верхнюю границу для
скорости передачи R.
2
• При доказательстве теоремы вводится показатель экспоненци-
альной оценки До, который может быть использован для оцен-
ки
технически достижимой скорости передачи данных [4|.
1
Теорема кодирования справедлива не только для дискретных каналов, она так-
же верна и при передаче дискретных сообщений по непрерывным каналам. -
Прим.
перев.
2
Здесь необходимо сделать разъяснение. Существует обратная теорема кодиро-
вания,
которая говорит о том, что при R > С не существует никакого метода
кодирования,
позволяющего передавать информацию с как угодно малой веро-
ятностью ошибки.- Прим.
перев.

ГЛАВА 8
НЕПРЕРЫВНЫЕ
ИСТОЧНИКИ
И КАНАЛЫ
В
главе
2 дано определение энтропии как меры неопределенности
источника. При этом предполагалось, что энтропия измеряется по-
средством случайных экспериментов. В данной
главе
мы
будем
при-
менять аналогичный
подход
к непрерывным источникам.
Источник
X
«г\/
\St
Рис.
8Д. Сигнал непрерывного источника.
Вместо источников с конечным алфавитом символов
будем
рас-
сматривать источники, выходом которых являются непрерывные сиг-
налы.
Примером таких сигналов может служить изменяющееся во
времени напряжение в телефонных каналах и т.д. На рисунке 8.1
представлен непрерывный источник X, выходом которого является
аналоговый сигнал x(t), являющийся некоторой случайной функци-
ей от времени t. Будем рассматривать значения x(t) в некоторые
фиксированные
моменты времени как случайные эксперименты, ко-
торые
несут
некоторую информацию об источнике X.
8.1.
Дифференциальная
энтропия
На
рисунке 8.2 показаны два непрерывных источника X и У, свя-
занные
каналом (аналогично рис. 7.4). Здесь, вместо вероятностей,
стоят функции плотностей распределения вероятностей стохастиче-
ских переменных.
Использование стохастических неременных и их функции плот-
ностей распределения вероятностей-позволяет вводить понятие ин-
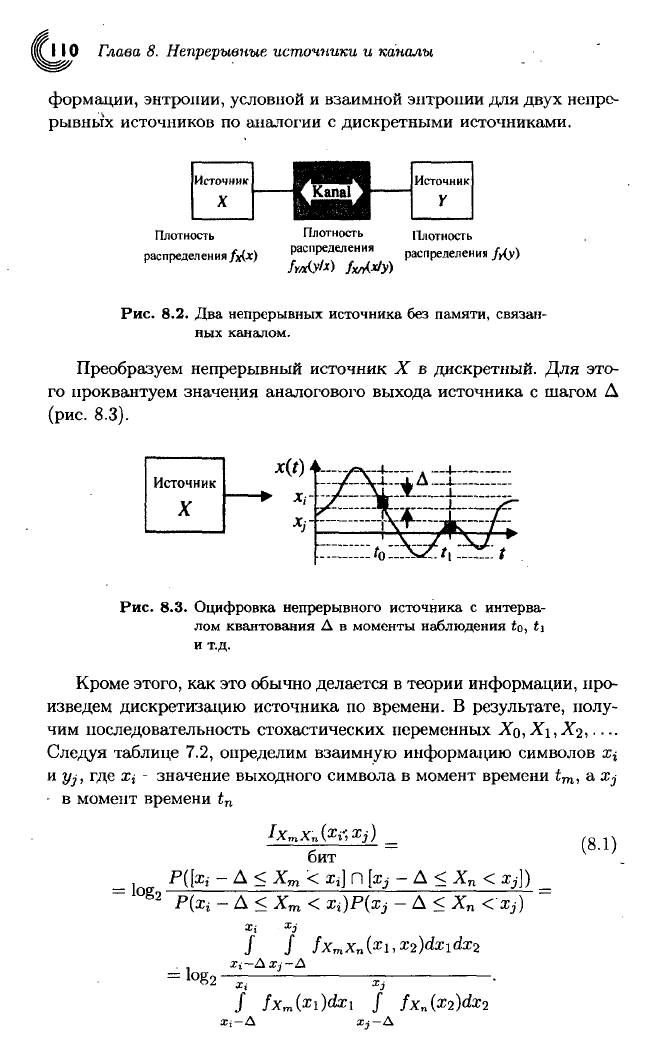
I
10 Глава 8. Непрерывные источники и каналы
формации,
энтропии, условной
и
взаимной энтропии для
двух
непре-
рывных источников
по
аналогии
с
дискретными источниками.
Источник
X
Плотность
распределения
)
Источник
Y
Плотность Плотность
распределения
расП
ред
елен
„
я
j
Рис.
8.2. Два
непрерывных источника
без
памяти, связан-
ных каналом.
Преобразуем непрерывный источник
X в
дискретный.
Для это-
го проквантуем значения аналогового
выхода
источника
с
шагом
Д
(рис.
8.3).
Источник
X
Рис.
8.3.
Оцифровка непрерывного источника
с
интерва-
лом квантования
Д в
моменты наблюдения
to, ti
и
т.д.
Кроме этого, как это обычно делается
в
теории информации, про-
изведем дискретизацию источника
по
времени.
В
результате,
полу-
чим последовательность стохастических переменных
Xo,Xi,X
2
,
Следуя таблице
7.2,
определим взаимную информацию символов
а^
и
yj, где Xi -
значение выходного символа
в
момент времени
t
m
, a Xj
-
в
момент времени
t
n
=
log
бит
P{\Xi - А < Х
т
<
Xi
] П |
j
- А < Х
п
<
Р(1; - А < Х
т
<
Xi)P(Xj
-А<Х
п
<
I
J
fx
m
x
n
{
x
i^
x
2)dxidx
2

8.1.
Дифференциальная
энтропия
Взаимную информацию можно трактовать как
«снятую»
(утра-
ченную) неопределенность попадания переменной Х
п
в интервале
[XJ
—
A,Xj[,
когда известно, что переменная Х
т
принадлежит интер-
валу
[xi — Д,Xi[ или наоборот. Будем считать функцию плотности
распределения вероятности непрерывной функцией. Тогда, устрем-
ляя
ширину интервала квантования к нулю, получим
Xi Xj
J J fx
m
x
n
(xi,x
2
)dxidx
2
/
fx
m
{xi)dx
x
J
Xi-Д Xj-Д
Afv
(T-\Afv
(r) • fv (rAfv (T-Y
т.е.
результат,
аналогичный выражению взаимной информации для
дискретных источников.
Передаваемую
информацию
можно опреде-
лить как математическое ожидание
(83)
бит
Замечание.
Здесь,
для
приведения
в
соответствие
обозначений
этой
главы
с
результатами
таблицы
7.2,
вместо
Х
т
используется
X, а
вместо
Y
n
- Y.
Информация
источника определяется исходя из аналогичных рас-
суждений
^
= -
log
2
Р([ХГ
-А<Х<
Xi
]) = (8.4)
Xi
=
-log
2
J
}
x
{xi)dx^
X
-lo
g2
(A/
x
fe))
=
Х
Г
-А ' . -
=
-log
2
A-log
2
/x(a:i).
В отличие от выражения (8.3) для взаимной информации, в (8.4)
появляется слагаемое, зависящее от интервала квантования Д.
При
Д —> оо, величина
log
2
(A)
также стремится к бесконечно-
сти. В результате, выражение для I{xi) также стремится к оо. Это
не
удивительно, так как с уменьшением шага квантования, число
отдельных событий (символов алфавита источника) возрастает и,
следовательно, неопределенность источника также растет.

Глава
8.
Непрерывные источники
и
каналы
Величина
log
2
(A)
не зависит
от
источника
и
совершенно не
умест-
на
для его описания,«поэтому, кажется вполне естественно использо-
вать только функцию плотности распределения вероятности непре-
рывного источника. Таким образом,
мы
переходим
к
следующему
определению.
Средняя информация непрерывного источника,
так
называемая
дифференциальная
энтропия,
определяется
как
Н(Х)
бит
/•оо
=
-/ f(x)log
2
f(x)dx. (8.5)
J
оо
Прежде всего отметим, что такое произвольное определение диф-
ференциальной энтропии подтверждает свою пригодность тем,
что
энтропийные
отношения
для
дискретных источников оказываются
справедливыми
и
для случая непрерывных источников
и
каналов.
В
частности,
для
непрерывных источников имеют место соотношения
(7.39)
-
(7.42).
Таким образом, дифференциальная энтропия непрерывного
ис-
точника зависит только
от
функции плотности распределения веро-
ятности, которая
в
общем
случае
является бесконечной величиной,
поэтому, поставим вопрос
о
том,
как
велико может быть значение
дифференциальной энтропии. Прежде всего отметим,
что
характе-
ристиками стохастического процесса являются
две
величины: сред-
нее значение, которое принимает стохастическая неременная (обла-
дающая свойством линейности)
ц и
стандартное отклонение
стоха-
стической переменной
а.
Среднее значение или математическое ожидание
/i не
оказывает
никакого
влияния
на
дифференциальную энтропию.
С
ростом
же а,
неопределенность источника возрастает,
что
приводит также
к
воз-
растанию дифференциальной энтропии.
В
связи
с
этим, сравнение
различных функций плотностей распределения вероятностей отно-
сительно соответствующих
им
энтропии имеет смысл производить
при
одинаковых
<х.
Замечание.
В
информационной
технике
за
исходный
параметр
принимают
<т
2
-
дисперсию,
которая
определяет
среднюю
мощ-
ность
стохастического
процесса
/10/.
Ясно,
что с
увеличением
мощности
передатчика,
количество
передаваемой
информации
уве-
личивается
и,
наоборот,
с
увеличением
мощности
шумов,
возрас-
тает
неопределенность,
т. е.
в
единицу
времени
передается
меньше
информации.
