Воробьев М.С. Устройства генерирования радиосигналов

81

Ɏɭɧɤɰɢɹ (7.22) ɨɩɢɫɵɜɚɟɬ ɤɨɷɮɮɢɰɢɟɧɬ ɩɟɪɟɞɚɱɢ ɤɨɥɟɛɚɧɢɣ ɫ ɱɚɫɬɨɬɨɣ,

ɨɬɥɢɱɚɸɳɟɣɫɹ ɨɬ

f

ɷɬ

ɧɚ

∆f

, ɟɫɥɢ ɬɚɤɨɜɵɟ ɩɪɢɫɭɬɫɬɜɭɸɬ ɜ ɫɩɟɤɬɪɟ ɤɨɥɟɛɚɧɢɣ

ɗȽ. ȼɢɞɧɨ, ɱɬɨ ɮɭɧɤɰɢɹ (7.22) ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɮɭɧɤɰɢɢ ɩɟɪɟɞɚɱɢ ɨɞɧɨɡɜɟɧɧɨɝɨ

Ɏɇɑ. ɉɨɷɬɨɦɭ ɫɢɫɬɟɦɵ ɎȺɉɑ ɛɟɡ Ɏɇɑ ɧɨɫɹɬ ɧɚɡɜɚɧɢɟ ɎȺɉɑ ɩɟɪɜɨɝɨ ɩɪɹɞɤɚ.

Ɋɚɫɫɦɨɬɪɢɦ ɢɯ ɨɫɧɨɜɧɵɟ ɫɜɨɣɫɬɜɚ. ɉɪɢ ɨɬɫɭɬɫɬɜɢɢ Ɏɇɑ ɜɵɯɨɞɧɨɟ ɧɚɩɪɹɠɟɧɢɟ

ɎȾ ɪɚɜɧɨ ɭɩɪɚɜɥɹɸɳɟɦɭ ɧɚɩɪɹɠɟɧɢɸ Ƚɍɇ

U

ɮɞ

= U

ɭɩɪ

. ɉɨɷɬɨɦɭ ɧɟɬɪɭɞɧɨ

ɨɩɪɟɞɟɥɢɬɶ ɩɨɥɨɫɵ ɭɞɟɪɠɚɧɢɹ ɢ ɡɚɯɜɚɬɚ ɱɚɫɬɨɬɵ, ɤɨɬɨɪɵɟ ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɛɭɞɭɬ

ɨɞɢɧɚɤɨɜɵɦɢ:

2

∆

f

ɡ

= 2

∆

f

ɭ

= 2U

ɮɞ max

S

ɝɭɧ

.

(7.23)

Ɏɢɥɶɬɪɭɸɳɢɟ ɫɜɨɣɫɬɜɚ ɫɢɫɬɟɦɵ ɯɚɪɚɤɬɟɪɢɡɭɸɬɫɹ ɩɨɥɨɫɨɣ ɩɪɨɩɭɫɤɚɧɢɹ ɧɚ

ɭɪɨɜɧɟ 0,707

Ω

= 1

/τ

ɮɚɩ

. (7.24)

Ⱦɥɹ ɩɟɪɟɯɨɞɚ ɢɡ ɚɫɢɧɯɪɨɧɧɨɝɨ ɪɟɠɢɦɚ ɜ ɫɢɧɯɪɨɧɧɵɣ ɧɟɨɛɯɨɞɢɦɨ ɧɟɤɨɬɨɪɨɟ

ɜɪɟɦɹ ɞɥɹ ɩɪɟɨɞɨɥɟɧɢɹ ɩɟɪɟɯɨɞɧɵɯ ɩɪɨɰɟɫɫɨɜ

t

ɭɫɬ

= 2,3

τ

ɮɚɩ

.

(7.25)

Ⱦɥɹ ɭɥɭɱɲɟɧɢɹ ɮɢɥɶɬɪɭɸɳɢɯ ɫɜɨɣɫɬɜ ɧɟɨɛɯɨɞɢɦɨ ɭɜɟɥɢɱɢɜɚɬɶ

τ

ɮɚɩ

, ɱɬɨ

ɭɜɟɥɢɱɢɜɚɟɬ ɢɧɟɪɰɢɨɧɧɨɫɬɶ ɫɢɫɬɟɦɵ ɢ ɭɦɟɧɶɲɚɟɬ ɩɨɥɨɫɭ ɭɞɟɪɠɚɧɢɹ. Ɍɚɤɢɦ

ɨɛɪɚɡɨɦ, ɪɚɡɧɵɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɫɢɫɬɟɦɵ ɨɩɪɟɞɟɥɹɸɬɫɹ ɨɞɧɢɦ ɢ ɬɟɦ ɠɟ ɩɚɪɚ-

ɦɟɬɪɨɦ, ɱɬɨ ɞɟɥɚɟɬ ɫɢɫɬɟɦɭ ɎȺɉɑ ɩɟɪɜɨɝɨ ɩɨɪɹɞɤɚ ɧɟɝɢɛɤɨɣ.

ȼɤɥɸɱɟɧɢɟ ɦɟɠɞɭ ɮɚɡɨɜɵɦ ɞɟɬɟɤɬɨɪɨɦ ɢ Ƚɍɇ ɨɞɧɨɡɜɟɧɧɨɝɨ Ɏɇɑ ɞɟɥɚɟɬ

ɫɢɫɬɟɦɭ ɎȺɉɑ ɬɨɠɞɟɫɬɜɟɧɧɨɣ ɞɜɭɯɡɜɟɧɧɨɦɭ ɮɢɥɶɬɪɭ. ɉɨɷɬɨɦɭ ɬɚɤɢɟ ɫɢɫɬɟɦɵ

ɩɨɥɭɱɢɥɢ ɧɚɡɜɚɧɢɟ ɎȺɉɑ ɜɬɨɪɨɝɨ ɩɨɪɹɞɤɚ. ɉɪɢɦɟɧɟɧɢɟ ɩɪɨɫɬɨɣ RC

ɢɧɬɟɝɪɢɪɭɸɳɟɣ ɰɟɩɨɱɤɢ, ɤɚɤ ɩɪɚɜɢɥɨ, ɧɟ ɞɚɟɬ ɫɭɳɟɫɬɜɟɧɧɨɝɨ ɩɪɟɢɦɭɳɟɫɬɜɚ

ɩɟɪɟɞ ɎȺɉɑ ɩɟɪɜɨɝɨ ɩɨɪɹɞɤɚ. ɉɨɷɬɨɦɭ ɧɚ ɩɪɚɤɬɢɤɟ ɧɚɢɛɨɥɶɲɟɟ

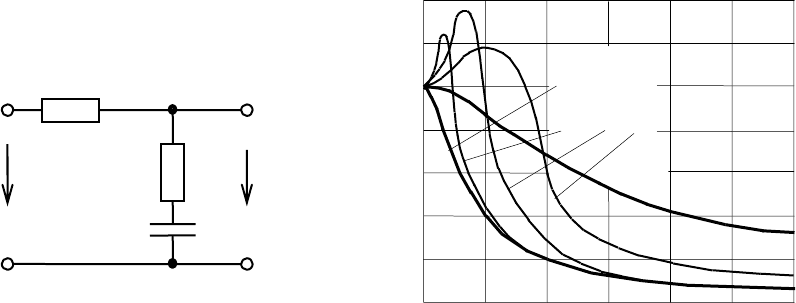
ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɟ ɩɨɥɭɱɢɥɢ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ-ɢɧɬɟɝɪɢɪɭɸɳɢɟ ɮɢɥɶɬɪɵ (ɪɢɫ.

7.9, ɚ).

W

1,2

R1 1,0

∆

=

∞

0,8 50 5 2

U

ɎȾ

R2 U

ɍɉɊ

0,6

∆

=0

C 0,4

0,2

0 1 2

∆ω

τ

ɮɚɩ

ɚ) ɛ)

Ɋɢɫ. 7.9. ɉɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɢɧɬɟɝɪɢɪɭɸɳɢɣ ɮɢɥɶɬɪ (ɚ) ɢ ɱɚɫɬɨɬɧɵɟ

ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɎȺɉɑ ɫ ɷɬɢɦ ɮɢɥɶɬɪɨɦ ɩɪɢ

q

= 0,2 (ɛ)

82

ɉɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɢɧɬɟɝɪɢɪɭɸɳɢɣ ɮɢɥɶɬɪ ɯɚɪɚɤɬɟɪɢɡɭɟɬɫɹ ɞɜɭɦɹ ɩɚɪɚ-

ɦɟɬɪɚɦɢ: ɨɬɧɨɫɢɬɟɥɶɧɨɣ ɩɨɫɬɨɹɧɧɨɣ ɜɪɟɦɟɧɢ

ɮɚɩ

ɮɧɱ

τ

=∆

,

(7.26)

ɝɞɟ

τ

ɮɧɱ

=

(R1+R2) C;

ɢ ɤɨɷɮɮɢɰɢɟɧɬɨɦ ɜɤɥɸɱɟɧɢɹ

q = R2/(R1+R2). (7.27)

ɇɚ ɪɢɫ. 7.9, ɛ ɩɨɤɚɡɚɧɵ ɱɚɫɬɨɬɧɵɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɫɢɫɬɟɦɵ ɎȺɉɑ ɫ ɩɪɨ-

ɩɨɪɰɢɨɧɚɥɶɧɨ-ɢɧɬɟɝɪɢɪɭɸɳɢɦ ɮɢɥɶɬɪɨɦ ɫ ɩɚɪɚɦɟɬɪɨɦ

q

= 0,2. ɑɚɫɬɧɵɣ

ɫɥɭɱɚɣ, ɤɨɝɞɚ

∆

= 0, ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɫɢɫɬɟɦɟ ɎȺɉɑ ɩɟɪɜɨɝɨ ɩɨɪɹɞɤɚ. ȼɢɞɧɨ, ɱɬɨ

ɩɪɢɦɟɧɟɧɢɟ Ɏɇɑ ɫɭɳɟɫɬɜɟɧɧɨ ɭɥɭɱɲɚɟɬ ɮɢɥɶɬɪɭɸɳɢɟ ɫɜɨɣɫɬɜɚ ɫɢɫɬɟɦɵ. ȼ

ɩɪɟɞɟɥɶɧɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ

∆

→ ∞, ɱɚɫɬɨɬɧɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ ɫɨɜɩɚɞɚɟɬ ɫ Ⱥɏɑ

ɫɢɫɬɟɦɵ ɛɟɡ ɮɢɥɶɬɪɚ, ɧɨ ɫ ɩɨɫɬɨɹɧɧɨɣ ɜɪɟɦɟɧɢ

τ

ɮɚɩ

, ɭɜɟɥɢɱɟɧɧɨɣ ɜ

1/q

ɪɚɡ.

ȼɚɠɧɨ, ɱɬɨ ɷɬɨ ɭɜɟɥɢɱɟɧɢɟ ɞɨɫɬɢɝɚɟɬɫɹ ɧɟ ɫɭɠɟɧɢɟɦ ɩɨɥɨɫɵ ɫɢɧɯɪɨɧɢɡɦɚ, ɚ

ɢɡɦɟɧɟɧɢɟɦ ɤɨɷɮɮɢɰɢɟɧɬɚ ɜɤɥɸɱɟɧɢɹ q.

ȼ ɪɟɚɥɶɧɵɯ ɫɢɫɬɟɦɚɯ ɨɬɧɨɫɢɬɟɥɶɧɚɹ ɩɨɫɬɨɹɧɧɚɹ ɜɪɟɦɟɧɢ ɜɵɛɢɪɚɟɬɫɹ

ɤɨɧɟɱɧɨɣ

∆ > 1

. ɉɪɢ ɷɬɨɦ ɞɨɛɢɜɚɸɬɫɹ ɷɮɮɟɤɬɢɜɧɨɝɨ ɩɨɞɚɜɥɟɧɢɹ ɩɨɦɟɯ ɫ

ɱɚɫɬɨɬɚɦɢ ∆

ω

> 1/

τ

ɮɚɩ

, ɧɨ ɨɞɧɨɜɪɟɦɟɧɧɨ ɧɟɡɧɚɱɢɬɟɥɶɧɨ ɭɫɢɥɢɜɚɸɬɫɹ ɩɨɦɟɯɢ ɫ

ɛɨɥɟɟ ɧɢɡɤɢɦɢ ɱɚɫɬɨɬɚɦɢ. Ɉɬɦɟɬɢɦ, ɱɬɨ ɩɪɨɫɬɚɹ ɢɧɬɟɝɪɢɪɭɸɳɚɹ ɰɟɩɨɱɤɚ

ɨɬɥɢɱɚɟɬɫɹ ɛɨɥɟɟ ɫɭɳɟɫɬɜɟɧɧɵɦɢ ɜɵɛɪɨɫɚɦɢ ɜ ɨɛɥɚɫɬɢ ɧɢɡɤɢɯ ɱɚɫɬɨɬ.

ɍɜɟɥɢɱɟɧɢɟ ɢɧɟɪɰɢɨɧɧɨɫɬɢ ɮɢɥɶɬɪɚ ɩɪɢɜɨɞɢɬ ɜ ɧɟɥɢɧɟɣɧɨɣ ɫɢɫɬɟɦɟ

ɎȺɉɑ ɤ ɝɢɫɬɟɪɟɡɢɫɧɵɦ ɹɜɥɟɧɢɹɦ ɩɪɢ ɜɯɨɞɟ ɜ ɫɢɧɯɪɨɧɢɡɦ. Ɉɧɢ ɩɪɨɹɜɥɹɸɬɫɹ ɜ

ɬɨɦ, ɱɬɨ ɩɨɥɨɫɚ ɡɚɯɜɚɬɚ ɫɬɚɧɨɜɢɬɫɹ ɡɧɚɱɢɬɟɥɶɧɨ ɦɟɧɶɲɟ ɩɨɥɨɫɵ ɭɞɟɪɠɚɧɢɹ.

Ɏɢɡɢɱɟɫɤɢɣ ɫɦɵɫɥ ɬɚɤɨɝɨ ɫɭɠɟɧɢɹ ɡɚɤɥɸɱɚɟɬɫɹ ɜ ɫɥɟɞɭɸɳɟɦ. ȼ ɚɫɢɧɯɪɨɧɧɨɦ

ɪɟɠɢɦ, ɤɨɝɞɚ ɫɢɫɬɟɦɚ ɎȺɉɑ ɟɳɟ ɧɟ ɜɨɲɥɚ ɜ ɫɬɚɰɢɨɧɚɪɧɵɣ ɪɟɠɢɦ, ɧɚ ɜɵɯɨɞɟ

ɮɚɡɨɜɨɝɨ ɞɟɬɟɤɬɨɪɚ ɧɚɛɥɸɞɚɟɬɫɹ ɩɟɪɟɦɟɧɧɨɟ ɧɚɩɪɹɠɟɧɢɟ ɛɢɟɧɢɣ ɫɨ ɫɪɟɞɧɟɣ

ɱɚɫɬɨɬɨɣ ∆

ω

. ȼɫɥɟɞɫɬɜɢɟ ɩɨɞɚɜɥɹɸɳɟɝɨ ɞɟɣɫɬɜɢɹ Ɏɇɑ ɭɩɪɚɜɥɹɸɳɟɟ

ɧɚɩɪɹɠɟɧɢɟ U

ɭɩɪ

ɭɦɟɧɶɲɚɟɬɫɹ, ɢ ɭɦɟɧɶɲɟɧɢɟ ɬɟɦ ɛɨɥɶɲɟ, ɱɟɦ ɛɨɥɶɲɟ ɪɚɡɧɨɫɬɶ

ɦɟɠɞɭ ɱɚɫɬɨɬɚɦɢ ɷɬɚɥɨɧɧɨɝɨ ɝɟɧɟɪɚɬɨɪɚ ɢ ɬɟɤɭɳɟɣ ɱɚɫɬɨɬɨɣ Ƚɍɇ.

ɉɨɥɟɡɧɨ ɫɪɚɜɧɢɬɶ ɩɨ ɨɫɧɨɜɧɵɦ ɩɚɪɚɦɟɬɪɚɦ ɢ ɫɜɨɣɫɬɜɚɦ ɫɢɫɬɟɦɵ ɎȺɉɑ ɢ

ɑȺɉɑ.

ɋɢɫɬɟɦɚ ɎȺɉɑ ɨɛɟɫɩɟɱɢɜɚɟɬ ɬɨɱɧɨɟ ɫɨɜɩɚɞɟɧɢɟ ɱɚɫɬɨɬɵ Ƚɍɇ ɫ ɱɚɫɬɨɬɨɣ

ɷɬɚɥɨɧɧɨɝɨ ɝɟɧɟɪɚɬɨɪɚ, ɨɛɥɚɞɚɟɬ ɯɨɪɨɲɟɣ ɩɨɦɟɯɨɡɚɳɢɳɟɧɧɨɫɬɶɸ. Ɉɞɧɚɤɨ ɷɬɚ

ɫɢɫɬɟɦɚ ɨɛɥɚɞɚɟɬ ɭɡɤɨɣ ɩɨɥɨɫɨɣ ɡɚɯɜɚɬɚ ɢ ɧɢɡɤɨɣ ɞɨɫɬɨɜɟɪɧɨɫɬɶ ɢɧɮɨɪɦɚɰɢɢ,

ɬɚɤ ɤɚɤ ɤɨɥɟɛɚɧɢɹ ɧɚ ɜɵɯɨɞɟ Ƚɍɇ ɫɭɳɟɫɬɜɭɸɬ ɢ ɜ ɨɬɫɭɬɫɬɜɢɢ ɫɢɧɯɪɨɧɢɡɦɚ.

ɋɢɫɬɟɦɚ ɑȺɉɑ ɨɛɟɫɩɟɱɢɜɚɟɬ ɧɚɫɬɪɨɣɤɭ ɧɚ ɡɚɞɚɧɧɭɸ ɱɚɫɬɨɬɭ ɫ ɧɟɤɨɬɨɪɨɣ

ɨɲɢɛɤɨɣ, ɧɨ ɨɛɥɚɞɚɟɬ ɛɨɥɟɟ ɲɢɪɨɤɨɣ ɩɨɥɨɫɨɣ ɡɚɯɜɚɬɚ, ɱɬɨ ɩɨɡɜɨɥɹɟɬ ɛɵɬɶ

ɭɜɟɪɟɧɧɵɦ ɜ ɩɪɚɜɢɥɶɧɨɫɬɢ ɧɚɫɬɪɨɣɤɢ Ƚɍɇ.

ɑɚɫɬɨ ɷɬɢ ɞɜɟ ɫɢɫɬɟɦɵ ɨɛɴɟɞɢɧɹɸɬ ɜ ɩɚɪɚɥɥɟɥɶɧɭɸ ɫɯɟɦɭ, ɢ ɫɢɫɬɟɦɚ ɑȺɉɑ

ɢɫɩɨɥɶɡɭɟɬɫɹ ɞɥɹ ɝɪɭɛɨɣ ɧɚɫɬɪɨɣɤɢ Ƚɍɇ, ɚ ɬɨɱɧɭɸ ɧɚɫɬɪɨɣɤɭ ɨɫɭɳɟɫɬɜɥɹɟɬ

ɫɢɫɬɟɦɚ ɎȺɉɑ.

83

Ƚɥɚɜɚ 8. ȺɆɉɅɂɌɍȾɇȺə ɆɈȾɍɅəɐɂə

8.1. ɏɚɪɚɤɬɟɪɢɫɬɢɤɢ ɚɦɩɥɢɬɭɞɧɨɣ ɦɨɞɭɥɹɰɢɢ

Ⱥɦɩɥɢɬɭɞɧɨ-ɦɨɞɭɥɢɪɨɜɚɧɧɵɟ (ȺɆ) ɤɨɥɟɛɚɧɢɹ ɷɬɨ ɨɞɢɧ ɢɡ ɜɢɞɨɜ ɪɚɞɢɨ-

ɫɢɝɧɚɥɨɜ, ɜ ɤɨɬɨɪɨɦ ɢɧɮɨɪɦɚɰɢɹ ɨ ɩɟɪɟɞɚɜɚɟɦɨɦ ɫɨɨɛɳɟɧɢɢ ɫɨɞɟɪɠɢɬɫɹ ɜ

ɢɡɦɟɧɹɸɳɟɣɫɹ ɜɨ ɜɪɟɦɟɧɢ ɚɦɩɥɢɬɭɞɟ. ɇɚɩɪɢɦɟɪ, ɬɨɤ ɜɨɡɛɭɠɞɟɧɢɹ ɚɧɬɟɧɧɵ

ɩɟɪɟɞɚɬɱɢɤɚ ɩɪɢ ɚɦɩɥɢɬɭɞɧɨɣ ɦɨɞɭɥɹɰɢɢ ɢɦɟɟɬ ɜɢɞ

i(t) = I(t)

⋅

cos(

ω

0

t +

ϕ

0

),

(8.1)

ɝɞɟ

I(t)

— ɚɦɩɥɢɬɭɞɚ ɬɨɤɚ, ɜɪɟɦɟɧɧɚɹ ɡɚɜɢɫɢɦɨɫɬɶ ɤɨɬɨɪɨɣ ɩɨɜɬɨɪɹɟɬ ɮɨɪɦɭ

ɩɟɪɟɞɚɜɚɟɦɨɝɨ ɫɢɝɧɚɥɚ;

ω

0

,

ϕ

0

— ɧɟɫɭɳɚɹ ɱɚɫɬɨɬɚ ɢ ɧɚɱɚɥɶɧɚɹ ɮɚɡɚ ɤɨɥɟɛɚɧɢɣ,

ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ. Ⱦɥɹ ɨɛɳɟɣ ɨɰɟɧɤɢ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɩɚɪɚɦɟɬɪɨɜ ȺɆ ɤɨɥɟɛɚɧɢɣ

ɫɱɢɬɚɸɬ, ɱɬɨ ɩɟɪɟɞɚɜɚɟɦɵɣ ɫɢɝɧɚɥ — ɝɚɪɦɨɧɢɱɟɫɤɢɟ ɤɨɥɟɛɚɧɢɹ ɫ ɱɚɫɬɨɬɨɣ

Ω

<<

ω

0

. ȼɵɪɚɠɟɧɢɟ (8.1) ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɦɨɠɧɨ ɩɟɪɟɩɢɫɚɬɶ ɜ ɛɨɥɟɟ ɤɨɧɤɪɟɬɧɨɦ

ɜɢɞɟ

i(t) = I

ɦɨɥ

(1+ m

⋅

cos

Ω

t) cos(

ω

0

t+

ϕ

0

),

(8.2)

ɝɞɟ

m

— ɤɨɷɮɮɢɰɢɟɧɬ (ɝɥɭɛɢɧɚ) ɦɨɞɭɥɹɰɢɢ;

I

ɦɨɥ

— ɚɦɩɥɢɬɭɞɚ ɬɨɤɚ ɜ ɪɟɠɢɦɟ

ɦɨɥɱɚɧɢɹ, ɬ.ɟ. ɤɨɝɞɚ ɩɟɪɟɞɚɱɢ ɢɧɮɨɪɦɚɰɢɢ ɧɟɬ. ɋɩɟɤɬɪ ȺɆ ɤɨɥɟɛɚɧɢɹ (8.2)

ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɫɭɦɦɭ ɧɟɫɭɳɟɝɨ ɤɨɥɟɛɚɧɢɹ ɢ ɞɜɭɯ ɛɨɤɨɜɵɯ ɫɨɫɬɚɜɥɹɸɳɢɯ

ɫ ɱɚɫɬɨɬɚɦɢ

ω

0

+

Ω

ɢ

ω

0

−

Ω

:

i(t) = I

ɦɨɥ

cos

ω

0

t + 0,5m I

ɦɨɥ

cos(

ω

0

+

Ω

)

t+ 0,5m I

ɦɨɥ

cos(

ω

0

−

Ω

)

t .

(8.3)

ɉɨɫɤɨɥɶɤɭ ɚɦɩɥɢɬɭɞɚ ɤɨɥɟɛɚɧɢɣ ɦɟɧɹɟɬɫɹ, ɬɨ ɦɟɧɹɸɬɫɹ ɢ ɷɧɟɪɝɟɬɢɱɟɫɤɢɟ

ɩɚɪɚɦɟɬɪɵ ɩɟɪɟɞɚɬɱɢɤɚ. Ⱦɥɹ ɤɨɥɟɛɚɧɢɹ ɜɢɞɚ (8.2) ɦɨɠɧɨ ɜɵɞɟɥɢɬɶ ɫɥɟɞɭɸɳɢɟ

ɪɟɠɢɦɵ: ɦɨɥɱɚɧɢɹ, ɜ ɤɨɬɨɪɨɦ ɚɦɩɥɢɬɭɞɚ ɬɨɤɚ ɜ ɚɧɬɟɧɧɟ

I

a

=

I

ɦɨɥ

; ɦɚɤ-

ɫɢɦɚɥɶɧɵɣ, ɜ ɤɨɬɨɪɨɦ

I

a

=

I

ɦɨɥ

(1+m)

; ɦɢɧɢɦɚɥɶɧɵɣ, ɜ ɤɨɬɨɪɨɦ

I

a

=

I

ɦɨɥ

(1

−

m)

. ɋɨɨɬɜɟɬɫɬɜɟɧɧɨ ɞɥɹ ɭɤɚɡɚɧɧɵɯ ɪɟɠɢɦɨɜ ɦɨɠɧɨ ɪɚɫɫɱɢɬɚɬɶ

ɦɢɧɢɦɚɥɶɧɭɸ ɢ ɦɚɤɫɢɦɚɥɶɧɭɸ ɦɨɳɧɨɫɬɢ, ɤɨɬɨɪɵɟ ɭɞɨɛɧɨ ɜɵɪɚɡɢɬɶ ɱɟɪɟɡ

ɦɨɳɧɨɫɬɶ ɜ ɪɟɠɢɦɟ ɦɨɥɱɚɧɢɹ:

P I R P P m P P m

ɦɨɥ ɦɨɥ ɧ ɦɨɥ ɦɨɥ

= = + = −

1

2

1 1

2 2 2

; ( ) ; ( ) ,

max min

ɝɞɟ

R

ɧ

— ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɧɚɝɪɭɡɤɢ (ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɢɡɥɭɱɟɧɢɹ ɚɧɬɟɧɧɵ). ɉɪɢ

m = 1

ɦɨɳɧɨɫɬɶ ɜ ɦɚɤɫɢɦɚɥɶɧɨɦ ɪɟɠɢɦɟ ɜ 4 ɪɚɡɚ ɛɨɥɶɲɟ, ɱɟɦ ɜ ɪɟɠɢɦɟ ɦɨɥ-

ɱɚɧɢɹ, ɜ ɦɢɧɢɦɚɥɶɧɨɦ — ɪɚɜɧɚ ɧɭɥɸ. ɋɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɦɨɳɧɨɫɬɢ ɡɚ ɩɟɪɢɨɞ

ɦɨɞɭɥɢɪɭɸɳɟɝɨ ɫɢɝɧɚɥɚ

( ) ( )

¸

¹

·

¨

©

§

+=Ω+=

³

2

0

2

1

1cos1

2

1

2

mPtdȍtmPP

ɦɨɥɦɨɥcp

π

, (8.5)

ɭɜɟɥɢɱɢɜɚɟɬɫɹ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɦɨɳɧɨɫɬɶɸ ɜ ɪɟɠɢɦɟ ɦɨɥɱɚɧɢɹ ɧɚ

0,5m

2

P

ɦɨɥ

ɡɚ

ɫɱɟɬ ɦɨɳɧɨɫɬɢ ɞɜɭɯ ɛɨɤɨɜɵɯ ɱɚɫɬɨɬ ɜ ɫɩɟɤɬɪɟ ɪɚɞɢɨɫɢɝɧɚɥɚ.

ȺɆ ɤɨɥɟɛɚɧɢɹ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɜ ɥɸɛɨɦ ɢɡ ɤɚɫɤɚɞɨɜ ɪɚɞɢɨɩɟɪɟɞɚɬɱɢɤɚ,

ɟɫɥɢ ɩɨ ɡɚɤɨɧɭ ɫɢɝɧɚɥɚ ɢɧɮɨɪɦɚɰɢɢ ɜɨɡɞɟɣɫɬɜɨɜɚɬɶ ɧɚ ɤɚɤɨɣ-ɥɢɛɨ ɩɚɪɚɦɟɬɪ

(8.4)

84

ɤɚɫɤɚɞɚ, ɨɬ ɤɨɬɨɪɨɝɨ ɡɚɜɢɫɢɬ ɚɦɩɥɢɬɭɞɚ ɜɵɯɨɞɧɵɯ ɤɨɥɟɛɚɧɢɣ. Ʉɚɫɤɚɞ ɩɟɪɟ-

ɞɚɬɱɢɤɚ, ɜ ɤɨɬɨɪɨɦ ɩɪɨɢɫɯɨɞɢɬ ɦɨɞɭɥɹɰɢɹ, ɧɚɡɵɜɚɸɬ ɦɨɞɭɥɢɪɭɟɦɵɦ. ɍɫɬ-

ɪɨɣɫɬɜɨ, ɜ ɤɨɬɨɪɨɦ ɜɵɪɚɛɚɬɵɜɚɟɬɫɹ ɭɩɪɚɜɥɹɸɳɢɣ ɫɢɝɧɚɥ (ɬɨɤ ɢɥɢ ɧɚɩɪɹɠɟɧɢɟ),

ɧɚɡɵɜɚɸɬ ɦɨɞɭɥɹɬɨɪɨɦ. Ʉɚɱɟɫɬɜɟɧɧɭɸ ɢ ɤɨɥɢɱɟɫɬɜɟɧɧɭɸ ɨɰɟɧɤɭ ɪɚɛɨɬɵ

ɦɨɞɭɥɢɪɭɟɦɨɝɨ ɤɚɫɤɚɞɚ ɦɨɠɧɨ ɫɞɟɥɚɬɶ ɫ ɩɨɦɨɳɶɸ ɦɨɞɭɥɹɰɢɨɧɧɵɯ

ɯɚɪɚɤɬɟɪɢɫɬɢɤ.

ɋɬɚɬɢɱɟɫɤɚɹ ɦɨɞɭɥɹɰɢɨɧɧɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ (ɋɆɏ) ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ

ɡɚɜɢɫɢɦɨɫɬɶ ɢɡɦɟɧɹɟɦɨɝɨ ɩɪɢ ɦɨɞɭɥɹɰɢɢ ɩɚɪɚɦɟɬɪɚ (ɚɦɩɥɢɬɭɞɵ ɬɨɤɚ ɢɥɢ

ɧɚɩɪɹɠɟɧɢɹ, ɦɨɳɧɨɫɬɢ) ɩɪɢ ɦɟɞɥɟɧɧɨɦ ɢɡɦɟɧɟɧɢɢ ɭɩɪɚɜɥɹɸɳɟɝɨ ɫɢɝɧɚɥɚ.

ɋɆɏ ɩɨɡɜɨɥɹɟɬ ɤɚɱɟɫɬɜɟɧɧɨ ɨɰɟɧɢɬɶ ɫɬɟɩɟɧɶ ɢɫɤɚɠɟɧɢɹ ɢɫɯɨɞɧɨɝɨ ɫɢɝɧɚɥɚ ɩɪɢ

ɩɪɟɨɛɪɚɡɨɜɚɧɢɢ ɜ ɪɚɞɢɨɫɢɝɧɚɥ. Ⱦɥɹ ɧɟɢɫɤɚɠɟɧɧɨɝɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɋɆɏ ɩɨ

ɬɨɤɭ ɢɥɢ ɩɨ ɧɚɩɪɹɠɟɧɢɸ ɞɨɥɠɧɚ ɛɵɬɶ ɥɢɧɟɣɧɨɣ, ɚ ɩɨ ɦɨɳɧɨɫɬɢ —

ɤɜɚɞɪɚɬɢɱɧɨɣ.

Ⱦɢɧɚɦɢɱɟɫɤɚɹ ɦɨɞɭɥɹɰɢɨɧɧɚɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ (ȾɆɏ) ɷɬɨ ɡɚɜɢɫɢɦɨɫɬɶ

ɤɨɷɮɮɢɰɢɟɧɬɚ ɦɨɞɭɥɹɰɢɢ

m

ɨɬ ɚɦɩɥɢɬɭɞɵ ɦɨɞɭɥɢɪɭɸɳɟɝɨ ɫɢɝɧɚɥɚ. ȾɆɏ

ɩɨɡɜɨɥɹɟɬ ɫɞɟɥɚɬɶ ɤɨɥɢɱɟɫɬɜɟɧɧɵɟ ɨɰɟɧɤɢ ɩɨɥɭɱɚɟɦɵɯ ȺɆ ɤɨɥɟɛɚɧɢɣ, ɚ ɬɚɤɠɟ

ɫɮɨɪɦɭɥɢɪɨɜɚɬɶ ɬɪɟɛɨɜɚɧɢɹ ɤ ɦɨɞɭɥɹɬɨɪɭ.

Ⱥɦɩɥɢɬɭɞɧɚɹ ɦɨɞɭɥɹɰɢɹ ɧɟ ɢɫɩɨɥɶɡɭɟɬɫɹ ɜ ɞɢɚɩɚɡɨɧɟ ɋȼɑ, ɜɜɢɞɭ ɟɟ

ɧɢɡɤɢɯ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɩɚɪɚɦɟɬɪɨɜ, ɩɥɨɯɨɣ ɩɨɦɟɯɨɭɫɬɨɣɱɢɜɨɫɬɢ ɢ ɬɪɭɞɧɨɫɬɢ

ɩɨɥɭɱɟɧɢɹ ɥɢɧɟɣɧɵɯ ɋɆɏ ɜ ɩɪɢɛɨɪɚɯ ɋȼɑ. ɉɨɷɬɨɦɭ ɭɫɬɪɨɣɫɬɜɚ ɞɥɹ ɩɨɥɭɱɟɧɢɹ

ȺɆ ɤɨɥɟɛɚɧɢɣ ɛɭɞɟɦ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɬɨɥɶɤɨ ɞɥɹ ɞɢɚɩɚɡɨɧɚ ɭɦɟɪɟɧɧɵɯ ɱɚɫɬɨɬ, ɜ

ɤɨɬɨɪɨɦ ɩɪɢɦɟɧɹɸɬɫɹ ɜ ɨɫɧɨɜɧɨɦ ɞɜɚ ɜɢɞɚ ɦɨɞɭɥɹɰɢɢ: ɧɚɩɪɹɠɟɧɢɟɦ ɫɦɟɳɟɧɢɹ

ɢ ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ. ɇɟɪɟɞɤɨ ɩɪɢɦɟɧɹɸ ɤɨɦɛɢɧɚɰɢɸ ɷɬɢɯ ɜɢɞɨɜ

ɦɨɞɭɥɹɰɢɢ.

8.2. Ɇɨɞɭɥɹɰɢɹ ɫɦɟɳɟɧɢɟɦ

ɉɪɢ ɦɨɞɭɥɹɰɢɢ ɫɦɟɳɟɧɢɟɦ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɫɢɝɧɚɥɨɦ ɢɧɮɨɪɦɚɰɢɢ

ɢɡɦɟɧɹɸɬ ɫɦɟɳɟɧɢɟ ɧɚ ɭɩɪɚɜɥɹɸɳɟɦ ɷɥɟɤɬɪɨɞɟ Ⱥɗ ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ:

E

ɫɦ

(t) = E

ɫɦ ɦɨɥ

+ U

Ω

cos

Ω

t

, (8.6)

ɝɞɟ

U

Ω

— ɚɦɩɥɢɬɭɞɚ ɦɨɞɭɥɢɪɭɸɳɟɝɨ ɫɢɝɧɚɥɚ,

E

ɫɦ ɦɨɥ

— ɧɚɩɪɹɠɟɧɢɟ ɫɦɟɳɟ-

ɧɢɹ ɜ ɪɟɠɢɦɟ ɦɨɥɱɚɧɢɹ. Ɂɚɜɢɫɢɦɨɫɬɶ ɚɦɩɥɢɬɭɞɵ 1-ɣ ɝɚɪɦɨɧɢɤɢ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ

ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ ɪɚɫɫɦɚɬɪɢɜɚɥɨɫɶ ɜ ɝɥɚɜɟ 1, ɨɬɤɭɞɚ ɫɥɟɞɭɟɬ, ɱɬɨ ɋɆɏ ɩɪɢ

ɦɨɞɭɥɹɰɢɢ ɫɦɟɳɟɧɢɟɦ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɮɭɧɤɰɢɢ

γ

1

(

θ

),

ɝɞɟ ɭɝɨɥ ɨɬɫɟɱɤɢ

θ

ɜɵɱɢɫɥɹɟɬɫɹ ɢɡ (1.10). ɋɆɏ ɩɨɥɭɱɚɟɬɫɹ ɩɪɢɧɰɢɩɢɚɥɶɧɨ ɧɟɥɢɧɟɣɧɨɣ (ɪɢɫ. 1.10).

Ⱦɥɹ ɰɟɥɟɣ ɦɨɞɭɥɹɰɢɢ ɢɫɩɨɥɶɡɭɟɬɫɹ ɧɟɛɨɥɶɲɨɣ ɭɱɚcɬɨɤ ɷɬɨɣ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ,

ɝɞɟ ɟɟ ɮɨɪɦɚ ɛɥɢɡɤɚ ɤ ɥɢɧɟɣɧɨɣ. ɉɨɷɬɨɦɭ ɩɨɥɭɱɢɬɶ ɧɟɢɫɤɚɠɟɧɧɭɸ ɦɨɞɭɥɹɰɢɸ

ɩɪɢ

m

= 1 ɧɟ ɭɞɚɟɬɫɹ, ɚ ɧɚ ɩɪɚɤɬɢɤɟ ɢɫɩɨɥɶɡɭɟɬɫɹ

m

< 0,6...0,7. Ɉɞɧɚɤɨ ɞɥɹ

ɨɰɟɧɤɢ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɫɨɨɬɧɨɲɟɧɢɣ ɛɭɞɟɦ ɜɫɟ ɠɟ ɫɱɢɬɚɬɶ ɡɚɜɢɫɢɦɨɫɬɶ

I

ɜɵɯ1

(E

ɫɦ

)

ɥɢɧɟɣɧɨɣ ɮɭɧɤɰɢɟɣ ɜ ɇɊ. ɉɨɥɟɡɧɨ ɬɚɤɠɟ ɪɚɫɫɦɨɬɪɟɬɶ ɋɆɏ ɞɥɹ

ɩɨɫɬɨɹɧɧɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ

I

ɜɵɯ0

(E

ɫɦ

),

ɤɨɬɨɪɭɸ ɬɚɤɠɟ ɛɭɞɟɦ

ɫɱɢɬɚɬɶ ɥɢɧɟɣɧɨɣ ɮɭɧɤɰɢɟɣ ɜ ɩɪɟɞɟɥɚɯ ɇɊ. ɉɪɢɛɥɢɠɟɧɧɨ ɷɬɢ ɮɭɧɤɰɢɢ ɦɨɠɧɨ

85

ɩɨɫɬɪɨɢɬɶ, ɫɨɟɞɢɧɢɜ ɬɨɱɤɭ ɡɚɩɢɪɚɧɢɹ Ⱥɗ (

I

ɜɵɯ1

=

I

ɜɵɯ0

= 0,

E

ɫɦ min

= E

′−

U

ɜɯ

) ɢ

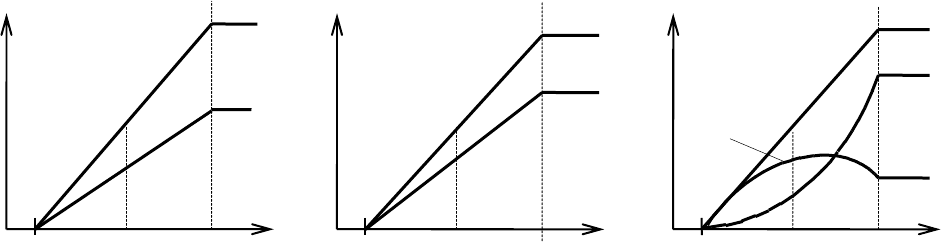
ɬɨɱɤɢ ɄɊ, ɚ ɜ ɉɊ ɬɨɤɢ ɛɭɞɟɦ ɫɱɢɬɚɬɶ ɩɨɫɬɨɹɧɧɵɦɢ (ɪɢɫ. 8.1, ɚ).

I

ɜɵɯ1

,

ξ

,

η

ɷ

P

0

,P

1

,

I

ɜɵɯ0

P

ɪɚɫ

I

ɜɵɯ1

I

ɜɵɯ0

ξ

P

0

η

ɷ

P

ɪɚɫ

P

1

E

ɫɦ

E

ɫɦ

E

ɫɦ

0

E

ɫɦ min

E

ɫɦ ɦɨɥ

E

ɫɦ max

0

E

ɫɦ min

E

ɫɦ ɦɨɥ

E

ɫɦ max

0

E

ɫɦ min

E

ɫɦ ɦɨɥ

E

ɫɦ max

ɚ) ɛ) ɜ)

Ɋɢɫ. 8.1. ɋɆɏ ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ ɩɪɢ ɦɨɞɭɥɹɰɢɢ ɫɦɟɳɟɧɢɟɦ

Ⱦɥɹ ɩɨɥɧɨɝɨ ɢɫɩɨɥɶɡɨɜɚɧɢɹ Ⱥɗ ɩɨ ɦɨɳɧɨɫɬɢ ɪɟɤɨɦɟɧɞɭɟɬɫɹ ɦɚɤɫɢɦɚɥɶɧɵɣ

ɪɟɠɢɦ ɜɵɛɢɪɚɬɶ ɤɪɢɬɢɱɟɫɤɢɦ, ɚ ɪɟɠɢɦ ɦɨɥɱɚɧɢɹ — ɩɨɫɪɟɞɢɧɟ ɥɢɧɟɣɧɨɝɨ

ɭɱɚɫɬɤɚ ɋɆɏ

I

ɜɵɯ1

(

E

ɫɦ

). Ⱦɥɹ ɭɦɟɧɶɲɟɧɢɹ ɢɫɤɚɠɟɧɢɣ ɭɝɨɥ ɨɬɫɟɱɤɢ ɜɵɯɨɞɧɨɝɨ

ɬɨɤɚ ɜ ɦɚɤɫɢɦɚɥɶɧɨɦ ɪɟɠɢɦɟ ɜɵɛɢɪɚɸɬ

Θ

max

= 110...120

ɨ

.

ɋ ɩɨɦɨɳɶɸ ɋɆɏ ɬɨɤɨɜ ɧɟɬɪɭɞɧɨ ɩɨɫɬɪɨɢɬɶ ɋɆɏ ɷɥɟɤɬɪɨɧɧɨɝɨ ɄɉȾ ɢ

ɦɨɳɧɨɫɬɟɣ (ɪɢɫ. 8.1, ɛ, ɜ). Ɂɚɜɢɫɢɦɨɫɬɶ

P

0

(

E

ɫɦ

) ɥɢɧɟɣɧɚ, ɩɨɷɬɨɦɭ ɦɨɳɧɨɫɬɶ,

ɩɨɬɪɟɛɥɹɟɦɚɹ ɨɬ ɢɫɬɨɱɧɢɤɚ ɩɢɬɚɧɢɹ, ɭɫɪɟɞɧɟɧɧɚɹ ɡɚ ɩɟɪɢɨɞ ɦɨɞɭɥɢɪɭɸɳɟɝɨ

ɫɢɝɧɚɥɚ

P

0 ɦɨɞ

(ɪɟɠɢɦ ɦɨɞɭɥɹɰɢɢ), ɪɚɜɧɚ ɦɨɳɧɨɫɬɢ ɜ ɪɟɠɢɦɟ ɦɨɥɱɚɧɢɹ.

ɗɥɟɤɬɪɨɧɧɵɣ ɄɉȾ ɜ ɪɟɠɢɦɟ ɦɨɞɭɥɹɰɢɢ

η

ɷ ɦɨɞ

=

P

ɫɪ

/

P

0 ɦɨɞ

=

η

ɷ ɦɨɥ

(1+0,5m

2

)

(8.7)

ɭɜɟɥɢɱɢɜɚɟɬɫɹ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɄɉȾ ɜ ɪɟɠɢɦɟ ɦɨɥɱɚɧɢɹ

η

ɷ ɦɨɥ

ɡɚ ɫɱɟɬ ɦɨɳɧɨɫɬɢ

ɛɨɤɨɜɵɯ ɩɨɥɨɫ, ɧɨ ɧɟɡɧɚɱɢɬɟɥɶɧɨ, ɩɨɫɤɨɥɶɤɭ ɫɪɟɞɧɟɫɬɚɬɢɫɬɢɱɟɫɤɨɟ ɡɧɚɱɟɧɢɟ

ɤɨɷɮɮɢɰɢɟɧɬɚ ɦɨɞɭɥɹɰɢɢ

m

ɫɪ

≈ 0,3.

ɉɟɪɟɞɚɬɱɢɤɢ ɫ ɦɨɞɭɥɹɰɢɟɣ ɫɦɟɳɟɧɢɟɦ ɢɦɟɸɬ ɧɢɡɤɢɣ ɄɉȾ, ɱɬɨ ɩɪɟ-

ɩɹɬɫɬɜɭɟɬ ɢɯ ɩɪɢɦɟɧɟɧɢɸ ɜ ɪɚɞɢɨɜɟɳɚɧɢɢ ɢ ɫɢɫɬɟɦɚɯ ɫɜɹɡɢ. Ɉɞɧɚɤɨ ɷɬɨɬ ɜɢɞ

ɦɨɞɭɥɹɰɢɢ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɫ ɩɨɦɨɳɶɸ ɦɚɥɨɦɨɳɧɨɝɨ ɦɨɞɭɥɹɬɨɪɚ, ɱɬɨ

ɢɫɩɨɥɶɡɭɟɬɫɹ, ɧɚɩɪɢɦɟɪ, ɜ ɬɟɥɟɜɢɞɟɧɢɢ, ɝɞɟ ɜɢɞɟɨɫɢɝɧɚɥ ɢɦɟɟɬ ɲɢɪɨɤɭɸ

ɩɨɥɨɫɭ.

8.3. ɍɫɢɥɟɧɢɟ ɦɨɞɭɥɢɪɨɜɚɧɧɵɯ ɤɨɥɟɛɚɧɢɣ

ȼ ɦɧɨɝɨɤɚɫɤɚɞɧɨɦ ɩɟɪɟɞɚɬɱɢɤɟ ɜɫɟ ɤɚɫɤɚɞɵ ɩɨɫɥɟ ɦɨɞɭɥɢɪɭɟɦɨɝɨ

ɪɚɛɨɬɚɸɬ ɜ ɪɟɠɢɦɟ ɭɫɢɥɟɧɢɹ ɦɨɞɭɥɢɪɨɜɚɧɧɵɯ ɤɨɥɟɛɚɧɢɣ. ɉɪɢ ɷɬɨɦ ɧɚ ɜɯɨɞ Ⱥɗ

ɩɨɞɚɟɬɫɹ ɦɨɞɭɥɢɪɨɜɚɧɧɨɟ ɧɚɩɪɹɠɟɧɢɟ ɜɨɡɛɭɠɞɟɧɢɹ

u

ɜɯ

(t) = U

ɜɯ ɦɨɥ

(1+m

ɜɯ

cos

Ω

t) cos

ω

0

t,

(8.8)

86

ɝɞɟ

m

ɜɯ

— ɤɨɷɮɮɢɰɢɟɧɬ ɦɨɞɭɥɹɰɢɢ ɧɚɩɪɹɠɟɧɢɹ ɜɨɡɛɭɠɞɟɧɢɹ. ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ

ɨɧ ɦɨɠɟɬ ɨɬɥɢɱɚɬɶɫɹ ɨɬ ɤɨɷɮɮɢɰɢɟɧɬɚ ɦɨɞɭɥɹɰɢɢ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ ɤɚɫɤɚɞɚ.

ɂɡɦɟɧɹɸɳɭɸɫɹ ɜɨ ɜɪɟɦɟɧɢ ɚɦɩɥɢɬɭɞɭ ɜɨɡɛɭɠɞɚɸɳɟɝɨ ɫɢɝɧɚɥɚ ɦɨɠɧɨ

ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɤɚɤ ɭɩɪɚɜɥɹɸɳɢɣ ɫɢɝɧɚɥ, ɚ ɭɫɢɥɢɬɟɥɶɧɵɣ ɤɚɫɤɚɞ — ɤɚɤ ɦɨɞɭ-

ɥɢɪɭɟɦɵɣ. ɉɨɷɬɨɦɭ ɞɥɹ ɨɰɟɧɤɢ ɪɚɛɨɬɵ Ⱥɗ ɜ ɷɬɨɦ ɪɟɠɢɦɟ ɧɟɨɛɯɨɞɢɦɵ ɋɆɏ ɩɨ

ɜɯɨɞɧɨɦɭ ɧɚɩɪɹɠɟɧɢɸ (ɪɢɫ. 1.9). Ⱦɥɹ ɧɚɢɦɟɧɶɲɟɝɨ ɢɫɤɚɠɟɧɢɹ

ɦɨɞɭɥɢɪɨɜɚɧɧɵɯ ɤɨɥɟɛɚɧɢɣ ɧɟɨɛɯɨɞɢɦɨ ɢɫɩɨɥɶɡɨɜɚɬɶ ɇɊ ɫ ɭɝɥɨɦ ɨɬɫɟɱɤɢ

Θ

= 90

ɨ

, ɬ.ɟ. ɩɪɢ

E

ɫɦ

=

E

′. ɉɪɢ

E

ɫɦ

<

E

′. ɋɆɏ ɹɜɥɹɟɬɫɹ ɧɟɥɢɧɟɣɧɨɣ, ɨɞɧɚɤɨ

ɢɦɟɟɬ ɞɨɜɨɥɶɧɨ ɩɪɨɬɹɠɟɧɧɵɣ ɧɚɱɚɥɶɧɵɣ ɥɢɧɟɣɧɵɣ ɭɱɚɫɬɨɤ, ɱɬɨ ɨɛɴɹɫɧɹɟɬɫɹ

ɨɞɧɨɜɪɟɦɟɧɧɵɦ ɪɨɫɬɨɦ ɚɦɩɥɢɬɭɞɵ ɜɯɨɞɧɨɝɨ ɧɚɩɪɹɠɟɧɢɹ ɢ ɭɝɥɚ ɨɬɫɟɱɤɢ. ɗɬɨɬ

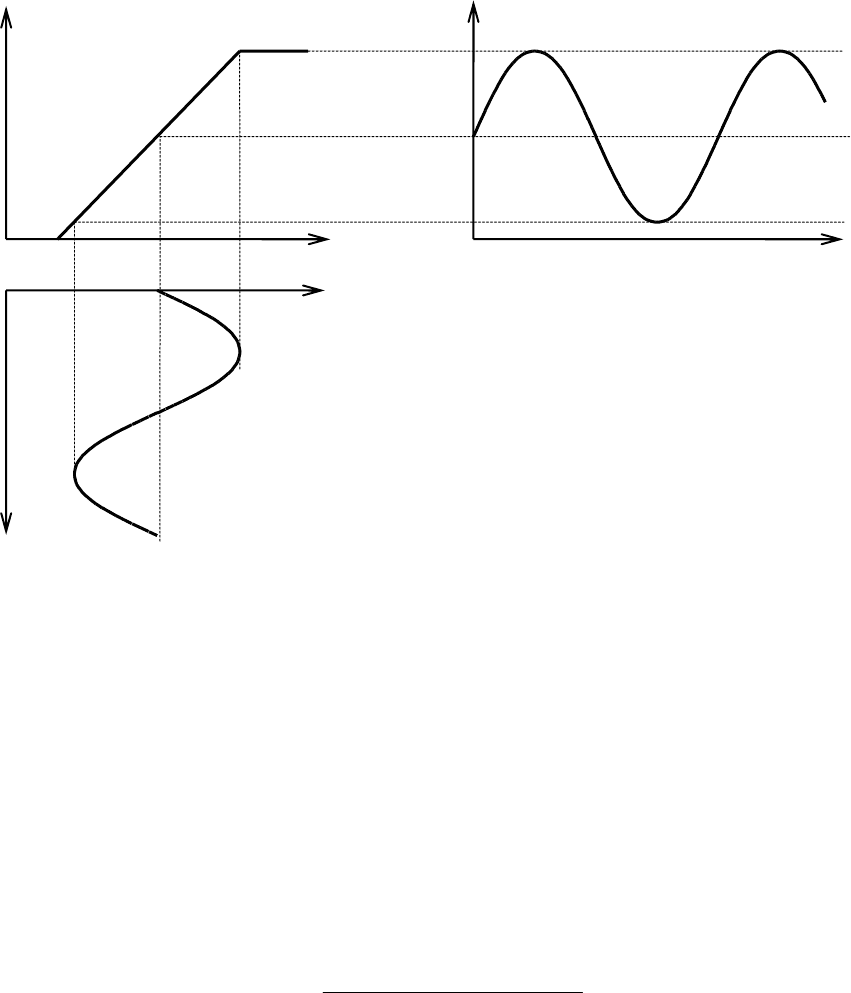
ɪɟɠɢɦ ɦɨɠɧɨ ɩɪɢɦɟɧɹɬɶ ɞɥɹ ɭɝɥɭɛɥɟɧɢɹ ɦɨɞɭɥɹɰɢɢ, ɱɬɨ ɧɚɝɥɹɞɧɨ ɩɨɤɚɡɚɧɨ ɧɚ

ɪɢɫ. 8.2.

I

ɜɵɯ1

I

ɜɵɯ1

=I

ɜɵɯ ɦɨɥ

(1+m

ɜɵɯ

cos

Ω

t)

⋅

I

ɜɵɯ max

I

ɜɵɯ ɦɨɥ

I

ɜɵɯ min

U

ɜɯ

Ω

t

U

ɜɯ

m

ɜɯ

= (U

ɜɯ max

−

U

ɜɯ min

)/(U

ɜɯ max

+ U

ɜɯ min

);

U

ɜɯ max

m

ɜɵɯ

= (I

ɜɵɯ max

−

I

ɜɵɯ min

)/(I

ɜɵɯ max

+ I

ɜɵɯ min

);

U

ɜɯ min

m

ɜɵɯ

> m

ɜɯ

.

Ω

t

Ɋɢɫ. 8.2. ɍɜɟɥɢɱɟɧɢɟ ɤɨɷɮɮɢɰɢɟɧɬɚ ɦɨɞɭɥɹɰɢɢ ɩɪɢ ɭɫɢɥɟɧɢɢ ȺɆ ɤɨɥɟɛɚɧɢɣ

Ɇɨɳɧɵɟ ɬɪɚɧɡɢɫɬɨɪɵ ɜɨɡɛɭɠɞɚɸɬɫɹ ɝɚɪɦɨɧɢɱɟɫɤɢɦ ɬɨɤɨɦ, ɚɦɩɥɢɬɭɞɚ

ɤɨɬɨɪɨɝɨ ɩɪɢ ɭɫɢɥɟɧɢɢ ȺɆ ɤɨɥɟɛɚɧɢɣ ɦɟɧɹɟɬɫɹ

I

ɛ 1

=

I

ɛ1 ɦɨɥ

(1+m cos

Ω

t),

(8.9)

ɱɬɨ ɩɪɢɜɨɞɢɬ ɧɟ ɬɨɥɶɤɨ ɤ ɢɡɦɟɧɟɧɢɸ ɚɦɩɥɢɬɭɞɵ ɤɨɥɥɟɤɬɨɪɧɨɝɨ ɬɨɤɚ

I

ɤ1

, ɧɨ ɢ ɤ

ɢɡɦɟɧɟɧɢɸ ɭɝɥɚ ɨɬɫɟɱɤɢ

Θ

. Ⱦɥɹ ɧɟɢɫɤɚɠɟɧɧɨɝɨ ɭɫɢɥɟɧɢɹ ȺɆ ɤɨɥɟɛɚɧɢɣ

ɩɨɫɥɟɞɧɢɣ ɧɟɨɛɯɨɞɢɦɨ ɩɨɞɞɟɪɠɢɜɚɬɶ ɩɨɫɬɨɹɧɧɵɦ. Ⱦɥɹ ɷɬɨɝɨ ɧɚɩɪɹɠɟɧɢɟ

ɫɦɟɳɟɧɢɹ ɞɨɥɠɧɨ ɢɡɦɟɧɹɬɶɫɹ ɩɨ ɡɚɤɨɧɭ

(

)

( )

Ĭ

C

tmI

EE

ɷ

ɦɨɥɛ

ɫɦ

−

Ω

+

−

′

=

πγ

ω

0

cos1

1

. (8.10)

87

Ɍɚɤɨɟ ɧɚɩɪɹɠɟɧɢɟ ɦɨɠɟɬ ɛɵɬɶ ɩɨɥɭɱɟɧɨ, ɟɫɥɢ

ɩɪɢɦɟɧɢɬɶ ɤɨɦɛɢɧɢɪɨɜɚɧɧɨɟ ɫɦɟɳɟɧɢɟ: ɮɢɤɫɢɪɨ-

ɜɚɧɧɨɟ, ɪɚɜɧɨɟ E′, ɢ ɚɜɬɨɦɚɬɢɱɟɫɤɨɟ ɡɚ ɫɱɟɬ ɩɪɨɬɟ-

ɤɚɧɢɹ ɩɨɫɬɨɹɧɧɨɝɨ ɬɨɤɚ ɛɚɡɵ

I

ɛ0

ɱɟɪɟɡ ɫɨɩɪɨ-

ɬɢɜɥɟɧɢɟ ɚɜɬɨɫɦɟɳɟɧɢɹ R

ɋɆ

(ɪɢɫ. 8.3). ɉɨɫɬɨɹɧɧɵɣ

ɬɨɤ ɛɚɡɵ

( )

Ĭ

h

I

h

I

ɷ

ɝɪ

ɛ

ɷ

ɤɨ

ɛ

0

2121

1

0

γ

ω

==

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɛɚɡɟ ɡɚ ɫɱɟɬ

ɤɨɦɛɢɧɢɪɨɜɚɧɧɨɝɨ ɫɦɟɳɟɧɢɹ

(

)

( )

ɫɦ

ɷ

ɝɪɦɨɥɛ

Ȼɫɦ

RĬ

h

tmI

UE

0

21

1

0

cos1

γ

ω

Ω

+

−=

. (8.11)

ɉɪɢɪɚɜɧɢɜɚɹ (8.10) ɢ (8.11) ɧɚɯɨɞɢɦ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɚɜɬɨɫɦɟɳɟɧɢɹ

(

)

( )

ɷɝɪ

ɷ

ɫɦ

ɋ

h

Ĭ

R

ωγ

π

γ

21

0

−

=

. (8.13)

ɗɧɟɪɝɟɬɢɱɟɫɤɢɟ ɩɚɪɚɦɟɬɪɵ ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ ɜ ɪɟɠɢɦɟ ɭɫɢɥɟɧɢɹ ȺɆ

ɤɨɥɟɛɚɧɢɣ ɩɨɥɭɱɚɸɬɫɹ ɬɚɤɢɦɢ ɠɟ, ɤɚɤ ɭ ɤɚɫɤɚɞɚ, ɦɨɞɭɥɢɪɭɟɦɨɝɨ ɧɚɩɪɹɠɟɧɢɟɦ

ɫɦɟɳɟɧɢɹ. Ⱦɥɹ ɩɨɜɵɲɟɧɢɹ ɄɉȾ ɪɟɤɨɦɟɧɞɭɟɬɫɹ ɦɚɤɫɢɦɚɥɶɧɵɣ ɪɟɠɢɦ ɞɟɥɚɬɶ

ɤɪɢɬɢɱɟɫɤɢɦ, ɚ ɪɟɠɢɦ ɦɨɥɱɚɧɢɹ — ɩɨɫɪɟɞɢɧɟ ɥɢɧɟɣɧɨɝɨ ɭɱɚɫɬɤɚ ɋɆɏ.

8.4. Ɇɨɞɭɥɹɰɢɹ ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ

Ɇɨɞɭɥɢɪɭɸɳɟɟ ɧɚɩɪɹɠɟɧɢɟ U

Ω

cos

Ω

t

ɜɤɥɸɱɚɸɬ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨ ɫ ɩɨɫ-

ɬɨɹɧɧɵɦ ɧɚɩɪɹɠɟɧɢɟɦ ɜ ɰɟɩɢ ɤɨɥɥɟɤɬɨɪɚ (ɢɥɢ ɚɧɨɞɚ)

E

ɉ

ɦɨɥ

, ɨɩɪɟɞɟɥɹɸɳɢɦ

ɪɟɠɢɦ ɦɨɥɱɚɧɢɹ:

E

ɉ

(

Ω

t

) =

E

ɉ

ɦɨɥ

+

U

Ω

cos

Ω

t

=

E

ɉ

ɦɨɥ

(1+m cos

Ω

t),

(8.13)

ɝɞɟ

m

=

U

Ω

/

E

ɉ

ɦɨɥ

. Ɋɚɫɫɦɨɬɪɢɦ ɷɧɟɪɝɟɬɢɱɟɫɤɢɟ ɫɨɨɬɧɨɲɟɧɢɹ ɩɪɢ ɦɨɞɭɥɹɰɢɢ

ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ, ɫɱɢɬɚɹ ɋɆɏ ɜɵɯɨɞɧɵɯ ɬɨɤɨɜ ɥɢɧɟɣɧɵɦɢ (ɪɢɫ. 1.11 ɢ

ɪɢɫ. 8.4,ɚ). Ʌɢɧɟɣɧɚɹ ɨɛɥɚɫɬɶ ɋɆɏ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɉɊ. ȼ ɉɊ ɤɨɷɮɮɢɰɢɟɧɬ

ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɧɚɩɪɹɠɟɧɢɹ

ξ

= =

U

ȿ

I R

ȿ

ɧ

ɉ

ɜɵɯ ɧ

ɩɉ

1

ɩɨɫɬɨɹɧɟɧ ɢ ɦɟɧɹɟɬɫɹ ɨɛɪɚɬɧɨ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ

ȿ

ɉ

ɜ ɨɛɥɚɫɬɢ ɇɊ. ɂ ɬɚɤ ɤɚɤ

ɤɨɷɮɮɢɰɢɟɧɬ ɮɨɪɦɵ ɬɨɤɚ

g

1

(

Θ

)

= const, ɬɨ ɷɥɟɤɬɪɨɧɧɵɣ ɄɉȾ ɡɚɜɢɫɢɬ ɨɬ

ȿ

ɉ

ɬɚɤ

ɠɟ, ɤɚɤ

ξ

ɨɬ

ȿ

ɉ

(ɪɢɫ.8.4, ɛ). Ɂɚɜɢɫɢɦɨɫɬɢ

P

0

(

ȿ

ɉ

),

P

1

(

ȿ

ɉ

) ɢ

P

ɪɚɫ

(

ȿ

ɉ

) ɜ ɉɊ ɢɦɟɸɬ

ɜɢɞ ɩɚɪɚɛɨɥ. ȼ ɇɊ ɦɨɳɧɨɫɬɶ

P

1

ɧɟɢɡɦɟɧɧɚɹ, ɚ

P

0

,

P

ɪɚɫ

ɭɜɟɥɢɱɢɜɚɸɬɫɹ ɥɢɧɟɣɧɨ

ɫ ɪɨɫɬɨɦ

ȿ

ɉ

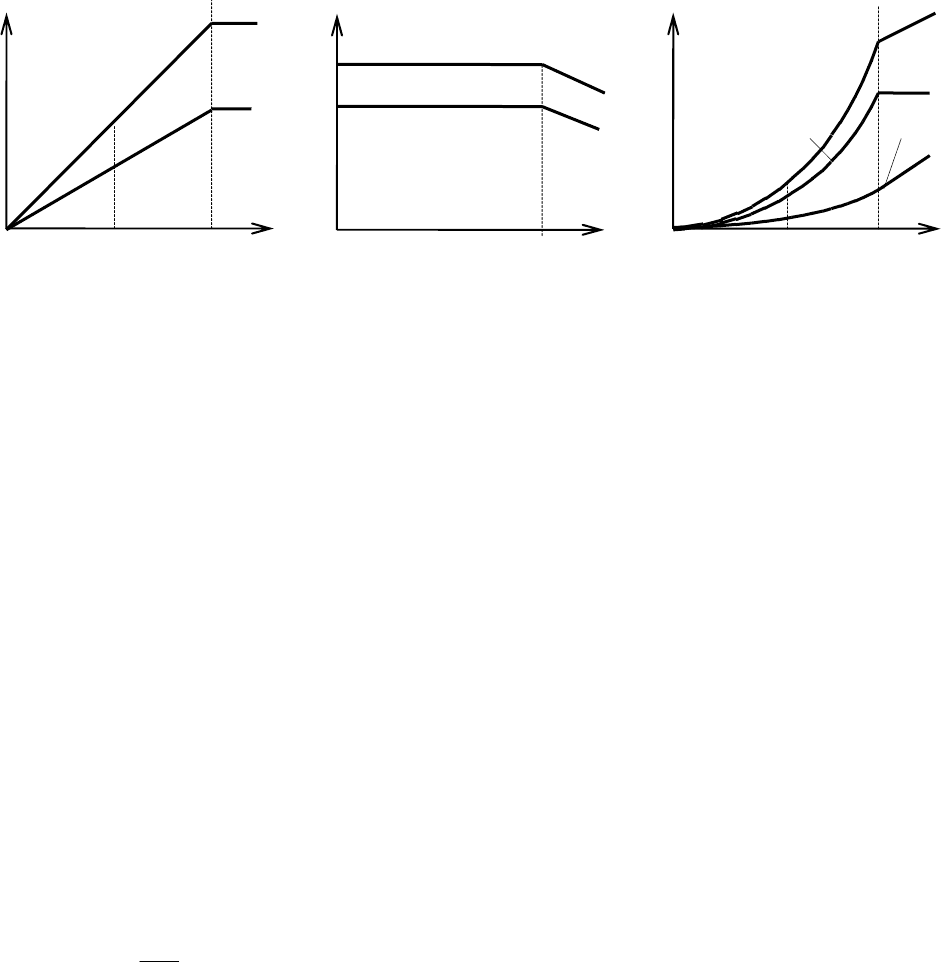
(ɪɢɫ. 8.4, ɜ).

R

ɋɆ

U

Ȼ0

C

ȻɅ

Ɋɢɫ. 8.3. Ʉɨɦɛɢɧɢɪɨɜɚɧ-

ɧɨɟ ɫɦɟɳɟɧɢɟ

88

I

ɜɵɯ1

,

ξ

,

η

ɷ

P

0

,P

1

,

I

ɜɵɯ0

ɉɊ ɇɊ

ξ

P

ɪɚɫ

I

ɜɵɯ1

I

ɜɵɯ0

η

ɷ

P

0

P

1

P

ɪɚɫ

E

ɉ

E

ɉ

E

ɉ

0

E

ɉ

ɦɨɥ

E

ɉ

max

0

E

ɉ

max

0

E

ɉ

ɦɨɥ

E

ɉ

max

ɚ) ɛ) ɜ)

Ɋɢɫ. 8.4. ɋɆɏ ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ ɩɪɢ ɦɨɞɭɥɹɰɢɢ ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ

Ⱦɥɹ ɥɭɱɲɟɝɨ ɢɫɩɨɥɶɡɨɜɚɧɢɹ Ⱥɗ ɪɟɤɨɦɟɧɞɭɸɬ ɦɚɤɫɢɦɚɥɶɧɵɣ ɪɟɠɢɦ

ɫɨɜɦɟɳɚɬɶ ɫ ɤɪɢɬɢɱɟɫɤɢɦ, ɚ ɪɟɠɢɦ ɦɨɥɱɚɧɢɹ — ɫ ɫɟɪɟɞɢɧɨɣ ɥɢɧɟɣɧɨɝɨ ɭɱɚɫɬɤɚ

ɋɆɏ. ɍɝɨɥ ɨɬɫɟɱɤɢ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ ɜ ɄɊ ɜɵɛɢɪɚɸɬ ɢɡ ɨɛɵɱɧɵɯ ɫɨɨɛɪɚɠɟɧɢɣ

(Θ = 70...90

ɨ

). ɗɥɟɤɬɪɨɧɧɵɣ ɄɉȾ ɜ ɦɚɤɫɢɦɚɥɶɧɨɦ ɪɟɠɢɦɟ ɞɨɫɬɚɬɨɱɧɨ ɜɵɫɨɤɢɣ

ɢ ɩɪɢ ɦɨɞɭɥɹɰɢɢ ɧɟ ɦɟɧɹɟɬɫɹ. ɗɬɨ ɜɚɠɧɨɟ ɩɪɟɢɦɭɳɟɫɬɜɨ ɦɨɞɭɥɹɰɢɢ

ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɦɨɞɭɥɹɰɢɟɣ ɫɦɟɳɟɧɢɟɦ.

Ɉɩɪɟɞɟɥɢɦ ɦɨɳɧɨɫɬɢ, ɨɬɞɚɜɚɟɦɵɟ ɢɫɬɨɱɧɢɤɨɦ ɩɢɬɚɧɢɹ

E

ɉ

ɦɨɥ

ɢ ɦɨɞɭ-

ɥɹɬɨɪɨɦ ɜ ɜɵɯɨɞɧɭɸ ɰɟɩɶ Ⱥɗ. ɉɨɫɤɨɥɶɤɭ ɋɆɏ ɩɨ ɬɨɤɭ ɥɢɧɟɣɧɵɟ ɢ ɩɪɨɯɨɞɹɬ

ɱɟɪɟɡ ɧɚɱɚɥɨ ɤɨɨɪɞɢɧɚɬ, ɬɨ ɤɨɷɮɮɢɰɢɟɧɬɵ ɦɨɞɭɥɹɰɢɢ ɩɨ ɬɨɤɭ ɢ ɧɚɩɪɹɠɟɧɢɸ

ɨɞɢɧɚɤɨɜɵɟ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ,

I

ɜɵɯ0

=

I

ɜɵɯ0 ɦɨɥ

(1+m cos

Ω

t).

(8.14)

ɍɫɪɟɞɧɟɧɧɚɹ ɦɨɳɧɨɫɬɶ ɡɚ ɩɟɪɢɨɞ ɦɨɞɭɥɢɪɭɸɳɟɝɨ ɫɢɝɧɚɥɚ

( ) ( )

ɦɨɥɜɵɯɦɨɞɦɨɥɜɵɯɦɨɞɦɨɞ

IȿtdtmIȿP

ɉɉɉ

00

2

cos1

2

1

0

=ΩΩ+=

³

π

. (8.15)

Ɇɨɳɧɨɫɬɶ, ɩɨɬɪɟɛɥɹɟɦɚɹ ɨɬ ɦɨɞɭɥɹɬɨɪɚ,

P

Ω

= 0,5 I

Ω

U

Ω

= 0,5m

2

P

ɉ

ɦɨɥ

, (8.16)

ɬ.ɟ. ɬɨɝɨ ɠɟ ɩɨɪɹɞɤɚ, ɱɬɨ ɢ ɦɨɳɧɨɫɬɶ, ɩɨɬɪɟɛɥɹɟɦɚɹ ɨɬ ɢɫɬɨɱɧɢɤɚ ɩɨɫɬɨɹɧɧɨɝɨ

ɧɚɩɪɹɠɟɧɢɹ.

Ɉɫɧɨɜɧɵɦɢ ɞɨɫɬɨɢɧɫɬɜɚɦɢ ɦɨɞɭɥɹɰɢɢ ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ ɹɜɥɹɸɬɫɹ

ɞɨɫɬɚɬɨɱɧɨ ɜɵɫɨɤɚɹ ɥɢɧɟɣɧɨɫɬɶ ɋɆɏ, ɜɵɫɨɤɢɟ ɄɉȾ ɢ ɤɨɷɮɮɢɰɢɟɧɬ ɦɨɞɭɥɹɰɢɢ

(m ≈ 1). ɋ ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ, ɦɨɞɭɥɹɰɢɹ ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ ɨɛɥɚɞɚɟɬ ɪɹɞɨɦ

ɧɟɞɨɫɬɚɬɤɨɜ: ɛɨɥɶɲɨɣ ɜɯɨɞɧɨɣ ɬɨɤ, ɫɜɹɡɚɧɧɵɣ ɫ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɉɊ; ɛɨɥɶɲɢɟ

ɦɨɳɧɨɫɬɢ ɜɨɡɛɭɠɞɟɧɢɹ ɢ ɧɢɡɤɢɣ ɤɨɷɮɮɢɰɢɟɧɬ ɭɫɢɥɟɧɢɹ; ɛɨɥɶɲɚɹ ɦɨɳɧɨɫɬɶ

ɪɚɫɫɟɹɧɢɹ ɧɚ ɭɩɪɚɜɥɹɸɳɟɦ ɷɥɟɤɬɪɨɞɟ (ɛɚɡɟ, ɫɟɬɤɟ); ɢɡɦɟɧɟɧɢɟ ɩɪɢ ɦɨɞɭɥɹɰɢɢ

ɜɯɨɞɧɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ; ɛɨɥɶɲɚɹ ɦɨɳɧɨɫɬɶ ɦɨɞɭɥɹɬɨɪɚ.

89

8.5. Ʉɨɦɛɢɧɢɪɨɜɚɧɧɵɟ ɦɟɬɨɞɵ ɦɨɞɭɥɹɰɢɢ

ȼɫɥɟɞɫɬɜɢɟ ɩɟɪɟɱɢɫɥɟɧɧɵɯ ɜɵɲɟ ɧɟɞɨɫɬɚɬɤɨɜ ɞɜɭɯ ɨɫɧɨɜɧɵɯ ɫɩɨɫɨɛɨɜ

ɦɨɞɭɥɹɰɢɢ, ɧɚ ɩɪɚɤɬɢɤɟ ɧɚɲɥɢ ɩɪɢɦɟɧɟɧɢɟ ɤɨɦɛɢɧɢɪɨɜɚɧɧɵɟ ɦɟɬɨɞɵ.

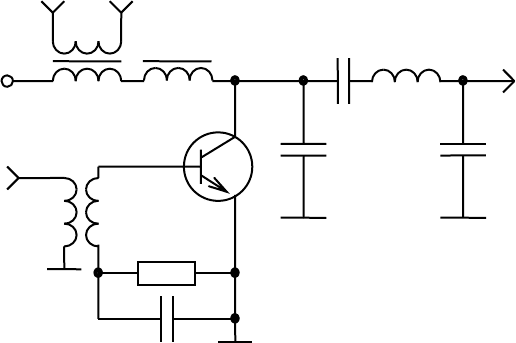
Ɇɨɞɭɥɹɰɢɹ ɫ ɚɜɬɨɫɦɟɳɟɧɢɟɦ (ɞɜɨɣɧɚɹ ɦɨɞɭɥɹɰɢɹ) ɩɨɤɚɡɚɧɚ ɧɚ ɪɢɫ. 8.5.

Ɂɞɟɫɶ ɢɫɩɨɥɶɡɨɜɚɧɚ ɤɨɥɥɟɤɬɨɪ-

ɧɚɹ ɦɨɞɭɥɹɰɢɹ. Ɇɨɞɭɥɢɪɭɸɳɢɣ

ɫɢɝɧɚɥ

U

Ω

ɩɨɞɚɟɬɫɹ ɱɟɪɟɡ

ɬɪɚɧɫɮɨɪɦɚɬɨɪ Ɍ, ɜɬɨɪɢɱɧɚɹ ɨɛ-

ɦɨɬɤɚ ɤɨɬɨɪɨɝɨ ɜɤɥɸɱɟɧɚ ɩɨɫɥɟ-

ɞɨɜɚɬɟɥɶɧɨ ɫ ɢɫɬɨɱɧɢɤɨɦ ɩɢɬɚ-

ɧɢɹ

E

ɉ

ɦɨɥ

. Ʉɪɨɦɟ ɷɬɨɝɨ,

ɫɨɡɞɚɟɬɫɹ ɞɨɩɨɥɧɢɬɟɥɶɧɚɹ ɦɨɞɭ-

ɥɹɰɢɹ ɧɚɩɪɹɠɟɧɢɹ ɫɦɟɳɟɧɢɹ

E

ɫɦ

ɡɚ ɫɱɟɬ ɩɪɨɬɟɤɚɧɢɹ ɩɨɫ-

ɬɨɹɧɧɨɝɨ ɬɨɤɚ ɛɚɡɵ ɱɟɪɟɡ ɫɨɩ-

ɪɨɬɢɜɥɟɧɢɟ R

ɋɆ

. ɉɪɢ ɭɜɟɥɢɱɟɧɢɢ

ɬɨɤɚ ɛɚɡɵ ɜ ɦɢɧɢɦɚɥɶɧɨɦ

ɪɟɠɢɦɟ ɨɞɧɨɜɪɟɦɟɧɧɨ ɜɨɡɪɚɫɬɚɟɬ ɩɚɞɟɧɢɟ ɧɚɩɪɹɠɟɧɢɹ ɧɚ R

ɋɆ

, ɱɬɨ ɨɝɪɚɧɢɱɢɜɚɟɬ

ɪɨɫɬ ɬɨɤɚ ɛɚɡɵ ɢ ɫɧɢɠɚɟɬ ɧɚɩɪɹɠɟɧɧɨɫɬɶ. Ⱦɜɨɣɧɚɹ ɦɨɞɭɥɹɰɢɹ ɩɨɡɜɨɥɹɟɬ, ɩɨ

ɫɪɚɜɧɟɧɢɸ ɫ ɨɛɵɱɧɨɣ ɦɨɞɭɥɹɰɢɟɣ ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ, ɩɨɥɭɱɢɬɶ ɛɨɥɟɟ

ɥɢɧɟɣɧɭɸ ɋɆɏ, ɦɟɧɶɲɢɣ ɞɢɚɩɚɡɨɧ ɢɡɦɟɧɟɧɢɹ ɜɯɨɞɧɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɢ

ɛɨɥɶɲɢɣ ɤɨɷɮɮɢɰɢɟɧɬ ɭɫɢɥɟɧɢɹ.

ɑɚɫɬɨ ɦɨɞɭɥɢɪɭɸɳɟɟ ɧɚɩɪɹɠɟɧɢɟ ɩɨɞɚɸɬ ɨɞɧɨɜɪɟɦɟɧɧɨ ɜ ɨɤɨɧɟɱɧɵɣ ɢ

ɩɪɟɞɨɤɨɧɟɱɧɵɣ ɤɚɫɤɚɞɵ. ȼ ɩɨɫɥɟɞɧɟɦ ɩɪɢɦɟɧɹɸɬ ɬɚɤɠɟ ɢ ɚɜɬɨɫɦɟɳɟɧɢɟ.

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɧɚ ɨɤɨɧɟɱɧɵɣ ɤɚɫɤɚɞ ɞɟɣɫɬɜɭɸɬ ɬɪɟɦɹ ɩɚɪɚɦɟɬɪɚɦɢ (ɬɪɨɣɧɚɹ

ɦɨɞɭɥɹɰɢɹ):

E

ɉ

,

E

ɫɦ

ɢ

U

ɜɯ

. Ɉɞɧɨɜɪɟɦɟɧɧɨɟ ɢɡɦɟɧɟɧɢɟ

U

ɜɯ

ɢ

E

ɫɦ

ɜ ɨɤɨɧɟɱɧɨɦ

ɤɚɫɤɚɞɟ ɩɨɡɜɨɥɹɟɬ ɨɫɬɚɜɥɹɬɶ ɧɟɢɡɦɟɧɧɵɦ ɭɝɨɥ ɨɬɫɟɱɤɢ, ɚ ɫɢɧɯɪɨɧɧɨɟ

ɢɡɦɟɧɟɧɢɟ

E

ɉ

ɢ

I

ɜɵɯ1

ɩɨɡɜɨɥɹɟɬ ɤɚɫɤɚɞɭ ɪɚɛɨɬɚɬɶ ɜ ɨɩɬɢɦɚɥɶɧɨɦ

ɷɧɟɪɝɟɬɢɱɟɫɤɨɦ ɪɟɠɢɦɟ (ɤɚɤ ɩɪɚɜɢɥɨ ɷɬɨ ɄɊ). Ɏɚɤɬɢɱɟɫɤɢ ɨɤɨɧɟɱɧɵɣ ɤɚɫɤɚɞ

ɜɵɩɨɥɧɹɟɬ ɪɨɥɶ ɭɫɢɥɢɬɟɥɹ ȺɆ ɤɨɥɟɛɚɧɢɣ.

ȿɳɟ ɨɞɧɚ ɪɚɡɧɨɜɢɞɧɨɫɬɶ ɤɨɦɛɢɧɢɪɨɜɚɧɧɨɣ ɦɨɞɭɥɹɰɢɢ ɫɜɹɡɚɧɚ ɫ ɢɫ-

ɩɨɥɶɡɨɜɚɧɢɟɦ ɷɤɪɚɧɢɪɨɜɚɧɧɵɯ ɥɚɦɩ (ɬɟɬɪɨɞɨɜ ɢɥɢ ɩɟɧɬɨɞɨɜ). ɉɪɢ ɚɧɨɞɧɨɣ

ɦɨɞɭɥɹɰɢɢ ɜ ɦɢɧɢɦɚɥɶɧɨɦ ɪɟɠɢɦɟ ɉɊ ɜɨɡɧɢɤɚɟɬ ɢ ɞɥɹ ɷɤɪɚɧɧɨɣ ɫɟɬɤɢ.

ɉɨɷɬɨɦɭ ɫɥɟɞɭɟɬ ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɷɤɪɚɧɧɨɣ ɫɟɬɤɢ ɦɟɧɹɬɶ ɫɢɧɯɪɨɧɧɨ ɢ ɫɢɧɮɚɡɧɨ

ɫ ɧɚɩɪɹɠɟɧɢɟɦ ɩɢɬɚɧɢɹ. ɗɬɨɬ ɜɢɞ ɦɨɞɭɥɹɰɢɢ ɧɨɫɢɬ ɧɚɡɜɚɧɢɟ ɚɧɨɞɧɨ-ɷɤɪɚɧɧɨɣ.

Ɉɛɳɢɣ ɧɟɞɨɫɬɚɬɨɤ ɜɫɟɯ ɜɢɞɨɜ ɦɨɞɭɥɹɰɢɢ ɫ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɢɡɦɟɧɟɧɢɹ

ɧɚɩɪɹɠɟɧɢɹ ɩɢɬɚɧɢɹ ɡɚɤɥɸɱɚɟɬɫɹ ɜ ɢɫɩɨɥɶɡɨɜɚɧɢɢ ɦɨɳɧɨɝɨ ɦɨɞɭɥɹɬɨɪɚ. ɄɉȾ

ɜɫɟɝɨ ɩɟɪɟɞɚɬɱɢɤɚ ɛɭɞɟɬ ɨɩɪɟɞɟɥɹɬɶɫɹ ɬɚɤɠɟ ɢ ɄɉȾ ɦɨɞɭɥɹɬɨɪɚ. Ɇɨɳɧɵɟ

ɜɵɯɨɞɧɵɟ ɤɚɫɤɚɞɵ ɦɨɞɭɥɹɬɨɪɨɜ, ɤɚɤ ɩɪɚɜɢɥɨ, ɫɬɪɨɹɬ ɩɨ ɞɜɭɯɬɚɤɬɧɨɣ ɫɯɟɦɟ ɫ

ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɬɪɚɧɫɮɨɪɦɚɬɨɪɨɜ. Ⱦɥɹ ɜɨɡɛɭɠɞɟɧɢɹ ɜɵɯɨɞɧɨɝɨ ɤɚɫɤɚɞɚ ɦɨɞɭ-

ɥɹɬɨɪɚ ɬɪɟɛɭɟɬɫɹ ɬɚɤɠɟ ɞɨɫɬɚɬɨɱɧɨ ɦɨɳɧɵɣ ɤɚɫɤɚɞ, ɧɚɡɵɜɚɟɦɵɣ ɩɨɞɦɨɞ-

ɭɥɹɬɨɪɨɦ.

U

Ω

Ɍ

E

ɉ

ɦɨɥ

L

ɛɥ

U

ɜɯ

R

ɋɆ

Ɋɢɫ. 8.5. Ɇɨɞɭɥɹɰɢɹ ɫ ɚɜɬɨɫɦɟɳɟɧɢɟɦ

90

Ƚɥɚɜɚ 9. ɈȾɇɈɉɈɅɈɋɇȺə ɆɈȾɍɅəɐɂə

9.1. Ɉɛɳɢɟ ɫɜɨɣɫɬɜɚ ɨɞɧɨɩɨɥɨɫɧɨɣ ɦɨɞɭɥɹɰɢɢ.

Ɍɢɩɵ ɢɡɥɭɱɟɧɢɹ

ȼ ȺɆ ɫɢɝɧɚɥɟ ɢɧɮɨɪɦɚɰɢɹ ɫɨɞɟɪɠɢɬɫɹ ɜ ɫɩɟɤɬɪɟ ɛɨɤɨɜɵɯ ɩɨɥɨɫ. Ʌɟɝɤɨ

ɡɚɦɟɬɢɬɶ, ɱɬɨ ɩɪɢ ɷɬɨɦ ɩɟɪɟɞɚɟɬɫɹ ɢɡɛɵɬɨɱɧɚɹ ɢɧɮɨɪɦɚɰɢɹ, ɩɨɫɤɨɥɶɤɭ ɜɫɟ

ɦɨɞɭɥɢɪɭɸɳɢɟ ɱɚɫɬɨɬɵ ɩɟɪɟɞɚɸɬɫɹ ɜ ɨɞɧɨɣ ɛɨɤɨɜɨɣ ɩɨɥɨɫɟ. ɉɨɷɬɨɦɭ

ɩɪɢɧɰɢɩɢɚɥɶɧɨ ɜɨɡɦɨɠɧɚ ɪɚɞɢɨɫɜɹɡɶ ɜ ɨɞɧɨɣ ɛɨɤɨɜɨɣ ɩɨɥɨɫɟ ɱɚɫɬɨɬ (ɈȻɉ),

ɤɨɬɨɪɚɹ ɢɦɟɟɬ ɩɟɪɟɞ ȺɆ ɪɹɞ ɩɪɟɢɦɭɳɟɫɬɜ.

• ȼ ɫɥɭɱɚɟ ɩɟɪɟɞɚɱɢ ɩɪɨɫɬɨɝɨ ɫɢɝɧɚɥɚ ɜ ɜɢɞɟ ɤɨɫɢɧɭɫɨɢɞɵ ɬɨɤ ɜ ɚɧɬɟɧɧɟ

ɦɟɧɹɟɬɫɹ ɩɨ ɝɚɪɦɨɧɢɱɟɫɤɨɦɭ ɡɚɤɨɧɭ:

(

)

tȍIi

ɛɨɤ

A

+

=

0

cos

ω

. (9.1)

Ⱥɦɩɥɢɬɭɞɚ ɬɨɤɚ

I

Ⱥ ɛɨɤ

ɡɚɜɢɫɢɬ ɨɬ ɤɨɷɮɮɢɰɢɟɧɬɚ m ɢ ɧɟ ɦɟɧɹɟɬɫɹ ɡɚ ɩɟɪɢɨɞ

ɦɨɞɭɥɢɪɭɸɳɟɝɨ ɫɢɝɧɚɥɚ. ɗɬɨ ɩɨɡɜɨɥɹɟɬ ɞɨɜɟɫɬɢ ɬɨɤ

I

Ⱥ ɛɨɤ

ɞɨ ɦɚɤɫɢ-

ɦɚɥɶɧɨɝɨ ɡɧɚɱɟɧɢɹ ɬɨɤɚ ɜ ɚɧɬɟɧɧɟ ɩɪɢ ȺɆ

(

)

mII

ɦɨɥ

ɛɨɤ

A

+

=

1

max

(9.2)

ɩɪɢ ɬɨɣ ɠɟ ɦɚɤɫɢɦɚɥɶɧɨɣ ɦɨɳɧɨɫɬɢ Ⱥɗ ɜɵɯɨɞɧɨɝɨ ɤɚɫɤɚɞɚ. ɉɨɥɟɡɧɵɣ

ɫɢɝɧɚɥ ɧɚ ɜɵɯɨɞɟ ɥɢɧɟɣɧɨɝɨ ɞɟɬɟɤɬɨɪɚ ɩɪɢɟɦɧɢɤɚ ɩɪɨɩɨɪɰɢɨɧɚɥɟɧ

m I

Ⱥ ɦɨɥ

:

ɦɨɥȺɆɞɟɬ

A

ImkU

=

, (9.3)

ɝɞɟ

k

— ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨɫɬɢ. ɇɚɩɪɹɠɟɧɢɟ ɧɚ ɜɵɯɨɞɟ

ɞɟɬɟɤɬɨɪɚ ɩɪɢɟɦɧɢɤɚ ɩɪɢ ɈȻɉ

(

)

mImkU

ɦɨɥɈȻɉɞɟɬ

A

+

=

1

, (9.4)

ɢ ɜɵɢɝɪɵɲ ɩɨ ɧɚɩɪɹɠɟɧɢɸ ɪɚɜɟɧ (1 +

m)/m, ɚ ɩɨ ɦɨɳɧɨɫɬɢ —

[(1 +

m)/m]

2

ɪɚɡ. ɇɚɩɪɢɦɟɪ, ɟɫɥɢ m = 1, ɬɨ ɜɵɢɝɪɵɲ ɩɨ ɦɨɳɧɨɫɬɢ ɫɨɫ-

ɬɚɜɥɹɟɬ 4 ɪɚɡɚ, ɚ ɟɫɥɢ

m = 0,5, ɬɨ 9 ɪɚɡ.

• ɋɩɟɤɬɪ ɱɚɫɬɨɬ, ɢɡɥɭɱɚɟɦɨɝɨ ɫɢɝɧɚɥɚ ɩɪɢ ɈȻɉ, ɭɦɟɧɶɲɚɟɬɫɹ ɜɞɜɨɟ, ɱɬɨ ɩɨɡ-

ɜɨɥɹɟɬ ɫɭɡɢɬɶ ɩɨɥɨɫɭ ɩɪɨɩɭɫɤɚɧɢɹ ɩɪɢɟɦɧɢɤɚ ɢ ɩɪɢ ɪɚɜɧɨɦɟɪɧɨɦ ɫɩɟɤɬɪɟ

ɲɭɦɚ ɩɪɢɜɨɞɢɬ ɤ ɭɜɟɥɢɱɟɧɢɸ ɨɬɧɨɲɟɧɢɹ ɫɢɝɧɚɥɚ ɤ ɲɭɦɭ ɜ 2 ɪɚɡɚ ɩɨ

ɦɨɳɧɨɫɬɢ. ɂɥɢ ɷɬɨ ɩɨɡɜɨɥɹɟɬ ɜɞɜɨɟ ɫɧɢɡɢɬɶ ɦɨɳɧɨɫɬɶ ɩɟɪɟɞɚɬɱɢɤɚ.

• Ⱦɥɹ ɩɟɪɟɞɚɬɱɢɤɨɜ ɤɨɪɨɬɤɨɜɨɥɧɨɜɨɝɨ ɞɢɚɩɚɡɨɧɚ ɩɪɢ ȺɆ ɢɡ-ɡɚ ɨɫɨɛɟɧ-

ɧɨɫɬɟɣ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ ɪɚɞɢɨɜɨɥɧ ɧɚɛɥɸɞɚɸɬɫɹ ɮɚɡɨɜɵɟ ɫɞɜɢɝɢ ɦɟɠɞɭ

ɧɟɫɭɳɟɣ ɢ ɛɨɤɨɜɵɦɢ ɱɚɫɬɨɬɚɦɢ, ɱɬɨ ɭɦɟɧɶɲɚɟɬ ɩɨɥɟɡɧɵɣ ɫɢɝɧɚɥ ɧɚ

ɜɵɯɨɞɟ ɩɪɢɟɦɧɢɤɚ. ɗɬɨɬ ɷɮɮɟɤɬ ɨɬɫɭɬɫɬɜɭɟɬ ɩɪɢ ɩɟɪɟɞɚɱɟ ɫ ɈȻɉ, ɱɬɨ

ɪɚɜɧɨɰɟɧɧɨ ɭɜɟɥɢɱɟɧɢɸ ɦɨɳɧɨɫɬɢ ɩɟɪɟɞɚɬɱɢɤɚ ɩɪɢɦɟɪɧɨ ɜ 2 ɪɚɡɚ.

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɨɛɳɢɣ ɜɵɢɝɪɵɲ ɩɨ ɦɨɳɧɨɫɬɢ ɩɪɢ ɩɟɪɟɯɨɞɟ ɨɬ ȺɆ ɤ ɦɨ-

ɞɭɥɹɰɢɢ ɈȻɉ ɫɨɫɬɚɜɥɹɟɬ 8…16 ɪɚɡ.

ɉɪɚɤɬɢɱɟɫɤɢ ɛɨɤɨɜɚɹ ɩɨɥɨɫɚ ɩɨɞɚɜɥɹɟɬɫɹ ɞɨ ɭɪɨɜɧɹ –40 ɞȻ ɨɬɧɨɫɢɬɟɥɶɧɨ

ɢɡɥɭɱɚɟɦɨɣ, ɚ ɧɟɫɭɳɚɹ ɦɨɠɟɬ ɛɵɬɶ ɩɨɞɚɜɥɟɧɚ ɥɢɲɶ ɱɚɫɬɢɱɧɨ. ɇɚ ɪɢɫ. 9.1

Воробьев М.С. Устройства генерирования радиосигналов

Подождите немного. Документ загружается.