Wai-Fah Chen.The Civil Engineering Handbook
Подождите немного. Документ загружается.


© 2003 by CRC Press LLC
[0 < x < 2]
[x > 0]
abx–()
1–
1
a
--
1
bx
a
-----
b
2
x
2
a
2
---------
b
3
x
3
a
3
--------- L++ ++= b
2
x
2
a
2
<[]
1 x±()
n
1 nx±
nn 1–()
2!
--------------------
x
2
nn 1–()n 2–()x
3
3!
------------------------------------------
± L+ += x
2
1<[]
1 x±()
n–
1 nx
+
−
nn 1+()
2!
---------------------
x
2
nn 1+()n 2+()
3!
--------------------------------------
x
3
+
−
L+ += x
2
1<[]
1 x±()
1
2
--
1
1
2
--
x±
1
24⋅
----------
x
2
–
13⋅
246⋅⋅
-----------------
x
3
±
135⋅⋅
2468⋅⋅⋅
-------------------------
x
4
– L±= x
2
1<[]
1 x±()
1
2
--
–
1
1
2
--
x
+
−
13⋅
24⋅
----------
x
2
135⋅⋅
246⋅⋅
-----------------
x
3
+
−
1357⋅⋅⋅
2468⋅⋅⋅
-------------------------
x
4
L
+
−
+ += x
2
1<[]
1 x
2
±()
1
2
--
1
1
2
--
x
2
±
x
4
24⋅
----------–
13⋅
246⋅⋅
-----------------
x
6
±
135⋅⋅
2468⋅⋅⋅
-------------------------
x
8
– L±= x
2
1<[]
1 x±()
1–
1 x
+
−
x
2
x
3
+
−
x
4
x
5
+
−
L
+++= x
2
1<[]
1 x±()
2–
12x
+
−
3x
2
4x
3
+
−
5x
4
L
+
−
+ += x
2
1<[]
e
x
1 x
x
2
2!
----
x
3
3!
----
x
4
4!
---- L++ +++=
e
x
2
–
1 x
2
–
x
4
2!
----
x
6
3!
----–
x
8
4!
---- L–++=
a
x
1 xalog
xalog()
2
2!
----------------------
xalog()
3
3!
---------------------- L++ + +=
xlog x 1–()
1
2
--
x 1–()
2
–
1
3
--
x 1–()
3
L–+=
xlog
x 1–
x
-----------
1
2
--
x 1–
x
-----------
2
1
3
--
x 1–
x
-----------
3
L+ + += x
1
2
--
>
x
l
og 2
x 1–
x 1+
------------
1
3
--
x 1–
x 1+
------------
3
1
5
--
x 1–
x 1+
------------
5
L+ + +=
1 x+()log x
1
2
--
x
2
–
1
3
--
x
3
1
4
--
x
4
– L+ += x
2
1<[]
1 x+
1 x–
------------
l
og 2 x
1
3
--
x
3
1
5
--
x
5
1
7
--
x
7
L++++= x
2
1<[]
x 1+
x 1–
------------
log 2
1
x
--
1
3
--
1
x
--
3
1
5
--
1
x
--
5
L+++= x
2
1>[]
© 2003 by CRC Press LLC
xsin x
x
3
3!
----–
x
5
5!
----
x
7
7!
----– L++=
xcos 1
x
2
2!
----–
x
4
4!
----
x
6
6!
----– L++=
xtan x
x
3
3
----
2x
5
15
--------
17x
7
315
---------- L
2
2n
2
2n
1–()B
2n 1–
x
2n 1–
2n()!
------------------------------------------------------++ +++= x
2
π
2
4
-----
<
ctn x
1
x
--
x
3
--–
x
3
45
-----–
2x
5
945
--------– L–
B
2n 1–
2x()
2n
2n()!x
----------------------------– L–= x
2
π
2
<[]
xsec 1
x
2
2!
----
5x
4
4!
--------
61x
6
6!
---------- L
B
2n
x
2n
2n()!
--------------- L++ ++++= x
2
π
2
4
-----
<
xcsc
1
x
--
x
3!
----
7x
3
35!⋅
------------
31x
5
37!⋅
------------ L
22
2n 1+
1–()
2n 2+()!
-----------------------------
B
2n 1+
x
2n 1+
L++ +++ += x
2
π
2
<[]
sin
1–
xx
x
3
6
----
13⋅()x
5
24⋅()5
--------------------
135⋅⋅()x
7
246⋅⋅()7
--------------------------- L++ + += x
2
1<[]
tan
1–
xx
1
3
--
x
3
–
1
5
--
x
5
1
7
--
x
7
– L+ += x
2
1<[]
sec
1–
x
π
2
---
1
x
--–
1
6x
3
--------–
13⋅
24⋅()5x
5
-----------------------–
135⋅⋅
246⋅⋅()7x
7
------------------------------– L–= x
2
1>[]
xsinh x
x
3
3!
----
x
5
5!
----
x
7
7!
---- L++++=
xcosh 1
x
2
2!
----
x
4
4!
----
x
6
6!
----
x
8
8!
---- L+++++=
xtanh 2
2
1–()2
2
B
1
x
2!
----
2
4
1–()2
4
B
3
x
3
4!
----
– 2
6
1–()2
6
B
5
x
5
6!
----
L–+= x
2
π
2
4
-----
<
ctnh x
1
x
--
1
2
2
B
1
x
2
2!
---------------
2
4
B
3
x
4
4!
---------------–
2
6
B
5
x
6
6!
--------------- L–+ +
= x
2
π
2
<[]
xsech 1
B
2
x
2
2!
----------–
B
4
x
4
4!
----------
B
6
x
6
6!
----------– L+ += x
2
π
2
4
-----
<
xcsch
1
x
-- 21–()2B
1
x
2!
----
– 2
3
1–()2B
3
x
3
4!
----
L–+= x
2
π
2
<[]
sinh
1–
xx
1
2
--
x
3
3
----
–
13⋅
24⋅
----------
x
5
5
----
135⋅⋅
246⋅⋅
-----------------
x
7
7
----
– L+ += x
2
1<[]
tanh
1–
xx
x
3
3
----
x
5
5
----
x
7
7
---- L++++= x
2
1<[]

© 2003 by CRC Press LLC
Error Function
The following function, known as the error function, erf x, arises frequently in applications:
The integral cannot be represented in terms of a finite number of elementary functions; therefore,
values of erf
x have been compiled in tables. The following is the series for erf x.
There is a close relation between this function and the area under the standard normal curve (Table 1
in the Tables of Probability and Statistics). For evaluation, it is convenient to use
z instead of x; then erf
z may be evaluated from the area F(z) given in Table 1 by use of the relation
Example
By interpolation from Table 1, F(0.707) = 0.260; thus, erf(0.5) = 0.520.
Series Expansion
The expression in parentheses following certain of the series indicates the region of convergence. If not
otherwise indicated, it is to be understood that the series converges for all finite values of
x.
Binomial
ctnh
1–
x
1
x
--
1
3x
3
--------
1
5x
5
-------- L+++= x
2
1>[]
csch
1–
x
1
x
--
1
23x
3
⋅
---------------–
13⋅
245x
5
⋅⋅
----------------------
135⋅⋅
2467x
7
⋅⋅⋅
------------------------------– L+ += x
2
1>[]
e
t
2
–
td
0
x
∫
x
1
3
--
x
3
–
x
5
52!⋅
------------
x
7
73!⋅
------------– L+ +=
erf x
2
π
-------
e
t
2
–
td
0
x
∫
=
erf x
2
π
-------
x
x
3
3
----–
x
5
52!⋅
------------
x
7
73!⋅
------------– L+ +=
erf z 2F 2z()=
erf 0.5() 2F 1.414()0.5()[ ] 2F 0.707()= =
xy+()
n
x
n
nx
n 1–
y
nn 1–()
2!
--------------------
x
n 2–
y
2
nn 1–()n 2–()
3!
-------------------------------------
x
n 3–
y
3
L++ + += y
2
x
2
<()
1 x±()
n
1 nx±
nn 1–()x
2
2!
-------------------------
nn 1–()n 2–()x
3
3!
------------------------------------------
± L etc.+ += x
2
1<()
1 x±()
n–
1 nx
+
−
nn 1+()x
2
2!
--------------------------
nn 1+()n 2+()x
3
3!
--------------------------------------------
+
−
L etc.+ += x
2
1<()
1 x±()
1–
1 x
+
−
x
2
x
3
x+
4
+
−
x
5
+
−
L+ += x
2
1<()
1 x±()
2–
12x
+
−
3x
2
4x
3
+
−
5x
4
6x
5
+
−
L+ + += x
2
1<()

© 2003 by CRC Press LLC
Reversion of Series
Let a series be represented by
to find the coefficients of the series
Taylor
1.
(Taylor’s series)
(Increment form)
2.
3. If f(x) is a function possessing derivatives of all orders throughout the interval a x b, then
there is a value
X, with a < X < b, such that
y
a
1
xa
2
x
2
a
3
x
3
a
4
x
4
a
5
x
5
a
6
x
6
L++++++= a
1
0≠()
xA
1
yA
2
y
2
A
3
y
3
A
4
y
4
L++++=
A
1
1
a
1
----
A
2
a
2
a
1
3
----
A
3
–
1
a
1
5
------
2a
2
2
a
1
a
3
–( )= = =
A
4
1
a
1
7
----
5a
1
a
2
a
3
a
1
2
a
4
– 5a
2
3
–( )=
A
5
1
a
1
9
----
6a
1
2
a
2
a
4
3a
1
2
a
3
2
14a
2
4
a
1
3
a
5
– 21a
1
a
2
2
a
3
–++( )=
A
6
1
a
1
11
------
7a
1
3
a
2
a
5
7a
1
3
a
3
a
4
84a
1
a
2
3
a
3
a
1
4
a
6
– 28a
1
2
a
2
2
a
4
– 28a
1
2
a
2
a
3
2
– 42a
2
5
–++( )=
A
7
1
a
1
13
------
(8a
1
4
a
2
a
6
8a
1
4
a
3
a
5
4a
1
4
a
4
2
120a
1
2
a
2
3
a
4
180a
1
2
a
2
2
a
3
2
132a
2
6
a
1
5
a
7
–+++ + +=
36a
1
3
a
2
2
a
5
– 72a
1
3
a
2
a
3
a
4
– 12a
1
3
a
3
3
– 330a
1
a
2
4
a
3
)–
fx() fa() xa–()f ′ a()
xa–()
2
2!
------------------
f ″ a()
xa–()
3
3!
------------------
f ′″ a()+ + +=
L
xa–()
n
n!
------------------
f
n()
a() L++ +
fx h+()fx() hf
′
x()
h
2
2!
-----
f ″ x()
h
3
3!
-----
f ′″ x() L++ ++=
fh() xf
′
h()
x
2
2!
----
f ″ h()
x
3
3!
----
f ′″ h() L++ ++=
fb() fa() ba–()f ′ a()
ba–()
2
2!
------------------
f ″ a()
L
+ + +=
ba–()
n 1–
n 1–()!
------------------------
f
n 1–()
a()
ba–()
n
n!
------------------
f
n()
X()+ +
fa h+()fa() hf ′ a()
h
2
2!
-----
f ″ a()
L
h
n 1–
n 1–()!
------------------
f
n 1–()
a()++ ++=
h
n
n!
-----
f
n()
a
θ
h+()b,+ ah0
θ
1<<,+=

© 2003 by CRC Press LLC
or
where
0 < θ < 1
The above forms are known as Taylor’s series with the remainder term.
4. Taylor’s series for a function of two variables:
etc., and if with the bar and subscripts means that after differentiation we
are to replace x by a and y by b,
then
MacLaurin
where
0 < θ < 1
Exponential
fx() fa() xa–()f ′ a()
xa–()
2
2!
------------------
f ″ a()
L
xa–()
n 1–
f
n 1–()
a()
n 1–()!
---------------------
R
n
+ + ++ +=
R
n
f
n()
a
θ
xa–()⋅+[ ]
n!
----------------------------------------------
xa–()
n
,=
If h
∂
∂
x
------
k
∂
∂
y
-----
+
fxy,()h
∂
fxy,()
∂
x
------------------
k
∂
fxy,()
∂
y
------------------
+=
and h
∂
∂
x
------
k
∂
∂
y
-----
+
2
fxy,()h
2
∂
2
fxy,()
∂
x
2
--------------------
2hk
∂
2
fxy,()
∂
x∂y
--------------------
k
2
∂
2
fxy,()
∂
y
2
--------------------
pp+ +=
h
∂
∂
x
------
k
∂
∂
y
------
+
n
fxy,()
yb=
xa=
fa hb k+,+( ) fab,()h
∂
∂
x
------
k
∂
∂
y
-----
+
fxy,()
xa=
yb=
L+ +=
1
n!
-----+ h
∂
∂
x
------
k
∂
∂
y
-----
+
n
fxy,()
xa=
yb=
L+
fx() f 0() xf ′ 0()
x
2
2!
----
f ″ 0()
x
3
3!
----
f ″′ 0() L x+
n 1–
f
n 1–()
0()
n 1–()!
---------------------
R
n
++ + + +=
R
n
x
n
f
n()
θ
x()
n!
------------------------
,=
e 1
1
1!
----
1
2!
----
1
3!
----
1
4!
---- L+++++=
e
x
1 x
x
2
2!
----
x
3
3!
----
x
4
4!
---- L (all real values of x)++ +++=
a
x
1 xa
x a
e
log()
2
2!
-------------------------+
e
x a
e
log()
3
3!
-------------------------+ L+log+=
e
x
e
a
1 xa–()
xa–()
2
2!
------------------
xa–()
3
3!
------------------ L++ ++
=

© 2003 by CRC Press LLC
Logarithmic
(a > 0, – a < x < + ∞)
(–1< x < 1)
(0 < x 2a)
Trigonometric
(all real values of x)
(all real values of x)
x
e
log
x 1–
x
-----------
1
2
--
x 1–
x
-----------
2
1
3
--
x 1–
x
-----------
3
L+ + += x
1
2
---
>()
x
e
log x 1–()
1
2
---
x 1–()
2
–
1
3
---
x 1–()
3
L–+= 2 x 0>≥()
x
e
l
og 2
x 1–
x 1+
------------
1
3
--
x 1–
x 1+
------------
3
1
5
--
x 1–
x 1+
------------
5
L+ + +
= x 0>()
1 x+()
e
log x
1
2
---
x
2
–
1
3
---
x
3
1
4
---
x
4
– L++= 1– x 1≤<()
n 1+()
e
n 1–()
e
log–log 2
1
n
---
1
3n
3
-------
1
5n
5
-------
L+++
=
ax+()
e
l
og a
e
2
x
2ax+
---------------
1
3
--
x
2ax+
---------------
3
1
5
--
x
2ax+
---------------
5
L+ + +
+log=
1 x+
1 x–
------------
e
log 2
x
x
3
3
----
x
5
5
----
L
x
2n 1–
2n 1–
--------------- L+++ ++
=
x
e
log a
xa–()
a
----------------
xa–()
2
2a
2
------------------–
xa–()
3
3a
3
------------------–+ +
e
log L+=
xsin x
x
3
3!
----
x
5
5!
----
x
7
7!
----– L++–=
xcos 1
x
2
2!
----
x
4
4!
----
x
6
6!
----– L++–=
xtan x
x
3
3
----
2x
5
15
--------
17x
7
315
----------
62x
9
2835
----------- L++ +++=
1–()
n 1–
2
2n
2
2n
1–()B
2n
2n()!
-------------------------------------------------------
x
2n 1–
L
x
2
π
2
4
-----
and B
n
represents the ,<
nth Bernoulli number
+ +
xcot
1
x
--
x
3
--
x
2
45
-----
–
2x
5
945
--------
–
x
7
4725
-----------– L––=
1–()
n 1+
2
2n
2n()!
--------------------------
– B
2n
x
2n 1–
L
x
2
π
2
and B
n
represents the ,<
nth Bernoulli number
–

© 2003 by CRC Press LLC
Differential Calculus
Notation
For the following equations, the symbols f (x), g (x), etc. represent functions of x. The value of a function
f (x) at x = a is denoted f (a). For the function y = f (x), the derivative of y with respect to x is denoted
by one of the following:
Higher derivatives are as follows:
and values of these at x = a are denoted f ″(a), f ″′(a), etc. (see Table of Derivatives).
Slope of a Curve
The tangent line at a point P(x, y) of the curve y = f (x) has a slope f
′
(x), provided that f ′(x) exists at P.
The slope at
P is defined to be that of the tangent line at P. The tangent line at P(x
1
, y
1
) is given by
The normal line to the curve at P(x
1
, y
1
) has slope –1 /f ′(x
1
) and thus obeys the equation
(The slope of a vertical line is not defined.)
Angle of Intersection of Two Curves
Two curves, y = f
1
(x) and y = f
2
(x), that intersect at a point P(X, Y) where derivatives f ′
1
(X), f ′
2
(X) exist
have an angle (
α) of intersection given by
If tan α > 0, then α is the acute angle; if tan α < 0, then α is the obtuse angle.
Radius of Curvature
The radius of curvature R of the curve y = f(x) at point P(x, y) is
In polar coordinates (
θ
, r), the corresponding formula is
dy
dx
------
f ′ x() D
x
y y′,,,
d
2
y
dx
2
--------
d
dx
------
dy
dx
------
d
dx
------
f ′ x() f ″ x()== =
d
3
y
dx
3
--------
d
dx
------
d
2
y
dx
2
--------
d
dx
------
f ″ x() f ″′ x() etc.,= = =
yy
1
– f ′ x
1
()xx
1
–()=
yy
1
– 1– f ′ x
1
()⁄[]xx
1
–()=
α
f ′
2
X() f ′
1
X()–
1 f ′
2
X()f ′
1
X()⋅+
---------------------------------------------=tan
R
1 f ′ x()[]
2
+{ }
32⁄
f ″ x()
-----------------------------------------=

© 2003 by CRC Press LLC
The curvature K is 1/R.
Relative Maxima and Minima
The function f has a relative maximum at x = a if f (a) ≥ f (a + c) for all values of c (positive or negative)
that are sufficiently near zero. The function
f has a relative minimum at x = b if f (b) ≤ f (b + c) for all
values of
c that are sufficiently close to zero. If the function f is defined on the closed interval x
1
≤ x ≤ x
2
and has a relative maximum or minimum at x = a, where x
1
< a < x
2
, and if the derivative f ′(x) exists
at
x = a, then f ′(a) = 0. It is noteworthy that a relative maximum or minimum may occur at a point
where the derivative does not exist. Further, the derivative may vanish at a point that is neither a maximum
nor a minimum for the function. Values of
x for which f ′(x) = 0 are called “critical values.” To determine
whether a critical value of
x, say x
c
, is a relative maximum or minimum for the function at x
c
, one may
use the second derivative test:
1. If f ″(x
c
) is positive, f (x
c
) is a minimum.
2. If f ″(x
c
) is negative, f (x
c
) is a maximum.
3. If f ″(x
c
) is zero, no conclusion may be made.
The sign of the derivative as x advances through x
c
may also be used as a test. If f ′(x) changes from
positive to zero to negative, then a maximum occurs at
x
c
, whereas a change in f ′(x) from negative to
zero to positive indicates a minimum. If
f ′(x) does not change sign as x advances through x
c
, then the
point is neither a maximum nor a minimum.
Points of Inflection of a Curve
The sign of the second derivative of f indicates whether the graph of y = f (x) is concave upward or
concave downward:
: concave upward
: concave downward
A point of the curve at which the direction of concavity changes is called a point of inflection
(Figure
29). Such a point may occur where f ″(x) = 0 or where f ″(x) becomes infinite. More precisely, if
the function y = f (x) and its first derivative y′ = f ′(x) are continuous in the interval a ≤ x ≤ b, and if y″ =
f ″(x) exists in a < x < b, then the graph of y = f (x) for a < x < b is concave upward if f ″(x) is positive
and concave downward if
f ″(x) is negative.
Taylor’s Formula
If f is a function that is continuous on an interval that contains a and x, and if its first (n + 1) derivatives
are continuous on this interval, then
where R is called the remainder. There are various common forms of the remainder:
R
r
2
dr
d
θ
------
2
+
32⁄
r
2
2
dr
d
θ
------
2
r
d
2
r
d
θ
2
--------
–+
---------------------------------------------=
f ″ x() 0>
f ″ x() 0<
f
x() fa() f ′ a()xa–()
f ″ a()
2!
-------------
xa–()
2
f ″′ a()
3!
---------------
xa–()
3
L
f
n()
a()
n!
---------------
xa–()
n
R+ + + ++ +=

© 2003 by CRC Press LLC
Lagrange’s Form
Cauchy’s Form
Integral Form
Indeterminant Forms
If f (x) and g(x) are continuous in an interval that includes x = a, and if f (a) = 0 and g(a) = 0, the limit
lim
x → a
(f (x)/g(x)) takes the form “0/0,” called an indeterminant form. L’Hôpital’s rule is
Similarly, it may be shown that if f (x) → ∞ and g(x) → ∞ as x → a, then
(The above holds for x → ∞.)
Examples
FIGURE 29 Point of inflection.
P
Rf
n 1+()
β
()
xa–()
n 1+
n 1+()!
------------------------
β
between a and x;⋅=
Rf
n 1+()
β
()
x
β
–()
n
xa–()
n!
-----------------------------------
β
between a and x;⋅=
R
xt–()
n
n!
-----------------
f
n 1+()
t() td
a
x
∫
=
fx()
gx()
----------
xa→
lim
f ′ x()
g′ x()
------------
xa→
lim=
fx()
gx()
----------
xa→
lim
f ′ x()
g′ x()
------------
xa→
lim=
xsin
x
-----------
x 0→
lim
xcos
1
------------
x 0→
lim 1= =
x
2
e
x
----
x ∞→
lim
2x
e
x
-----
x ∞→
lim
2
e
x
----
x ∞→
lim 0===
© 2003 by CRC Press LLC
Numerical Methods
a. Newton’s method for approximating roots of the equation f (x) = 0: A first estimate x
1 o
f the root
is made; then, provided that
f ′(x
1
) ≠ 0, a better approximation is x
2
:
The process may be repeated to yield a third approximation x
3 t
o the root:
provided f ′(x
2
) exists. The process may be repeated. (In certain rare cases, the process will not
converge.)
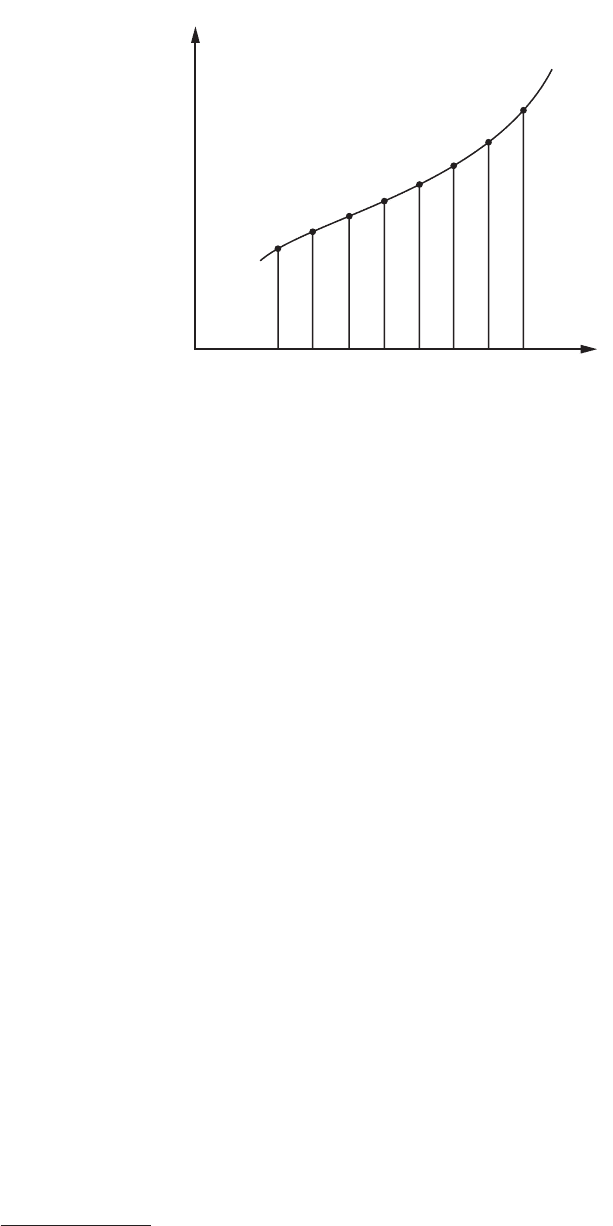
b. Trapezoidal rule for areas (Figure 30): For the function y = f (x) defined on the interval (a, b) and
positive there, take
n equal subintervals of width ∆x = (b – a) / n. The area bounded by the curve
between
x = a and x = b (or definite integral of f (x)) is approximately the sum of trapezoidal
areas, or
Estimation of the error (E) is possible if the second derivative can be obtained:
where c is some number between a and b.
Functions of Two Variables
For the function of two variables, denoted z = f (x, y), if y is held constant, say at y = y
1
, then the resulting
function is a function of
x only. Similarly, x may be held constant at x
1
, to give the resulting function of y.
FIGURE 30 Trapezoidal rule for area.
y
y
0
y
n
x
0a b
∆x
x
2
x
1
fx
1
()
f ′ x
1
()
--------------–=
x
3
x
2
fx
2
()
f ′ x
2
()
--------------–=
A
1
2
--
y
0
y
1
y
2
L y
n 1–
1
2
--
y
n
+++ ++
x∆()∼
E
ba–
12
-----------
f ″ c() x∆()
2
=
